import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.stats.multicomp import pairwise_tukeyhsd
np.random.seed(42) # für reproduzierbare ErgebnisseANOVA: Mittelwertvergleiche bei mehr als zwei Gruppen
Im vorangegangenen Kapitel haben wir t-Tests kennengelernt, mit denen wir Mittelwerte zweier Gruppen vergleichen können. Doch was tun wir, wenn wir mehr als zwei Gruppen vergleichen möchten? Wir könnten einfach mehrere t-Tests durchführen oder aber eine Varianzanalyse (Analysis of Variance, kurz ANOVA). In diesem Kapitel werden wir lernen, wie wir mit der ANOVA Mittelwerte mehrerer Gruppen gleichzeitig vergleichen können, und sehen, wie dies mit den linearen Modellen zusammenhängt, die wir bereits kennengelernt haben.
Das multiple Testproblem
Nehmen wir an, wir möchten alle drei Pinguinarten aus dem Palmer Penguins Datensatz hinsichtlich ihres Körpergewichts vergleichen:
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
Code zeigen/verstecken
# Funktion aus dem letzten Kapitel wiederverwenden
def plot_species(df, species_list, ref_value=None):
"""
Erstellt einen Jitter-Plot des Körpergewichts (body_mass_g) für eine oder mehrere Pinguinarten.
"""
# Plot-Setup
fig, ax = plt.subplots(figsize=(7, 4), layout='tight')
# Filtere nur relevante Arten und entferne NA-Werte in 'body_mass_g'
df_plot = df[df['species'].isin(species_list)].dropna(subset=['body_mass_g'])
# x-Positionen auf der Achse für jede Art
x_positions = {sp: i for i, sp in enumerate(species_list)}
# Durchlaufe alle gewünschten Arten
for species in species_list:
# Wähle Daten für die aktuelle Art
data = df_plot[df_plot['species'] == species]['body_mass_g']
# Erzeuge leicht gestreute x-Werte (Jitter), damit sich Punkte nicht überlappen
x_jitter = np.random.normal(loc=x_positions[species], scale=0.05, size=len(data))
# Streudiagramm der Einzelbeobachtungen
ax.scatter(x_jitter, data, alpha=0.7, s=20, color=colors[species])
# Berechne und plotte den Mittelwert als gestrichelte Linie
mean_val = data.mean()
ax.hlines(y=mean_val, xmin=x_positions[species]-0.2, xmax=x_positions[species]+0.2,
colors="black", linestyles='--', linewidth=2)
# Textbeschriftung für den Mittelwert
ax.text(x_positions[species]+0.25, mean_val, f"{mean_val:.0f} g",
va='center', ha='left', fontsize=9, color=colors[species])
# Optional: Referenzwert für Ein-Stichproben-Test (nur bei einer Art)
if ref_value is not None and len(species_list) == 1:
ax.hlines(y=ref_value, xmin=-0.2, xmax=0.2, colors='red', linestyles='-', linewidth=2)
ax.text(0.25, ref_value, f"{ref_value} g (Referenzwert)", va='center', ha='left',
fontsize=9, color='red')
# Achsenbeschriftungen und kosmetische Einstellungen
ax.set_ylabel('Körpergewicht (g)')
ax.set_xticks(list(x_positions.values()))
ax.set_xticklabels(species_list)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# Plot anzeigen
plt.show()# Alle drei Pinguinarten vergleichen
plot_species(penguins, ['Adelie', 'Chinstrap', 'Gentoo'])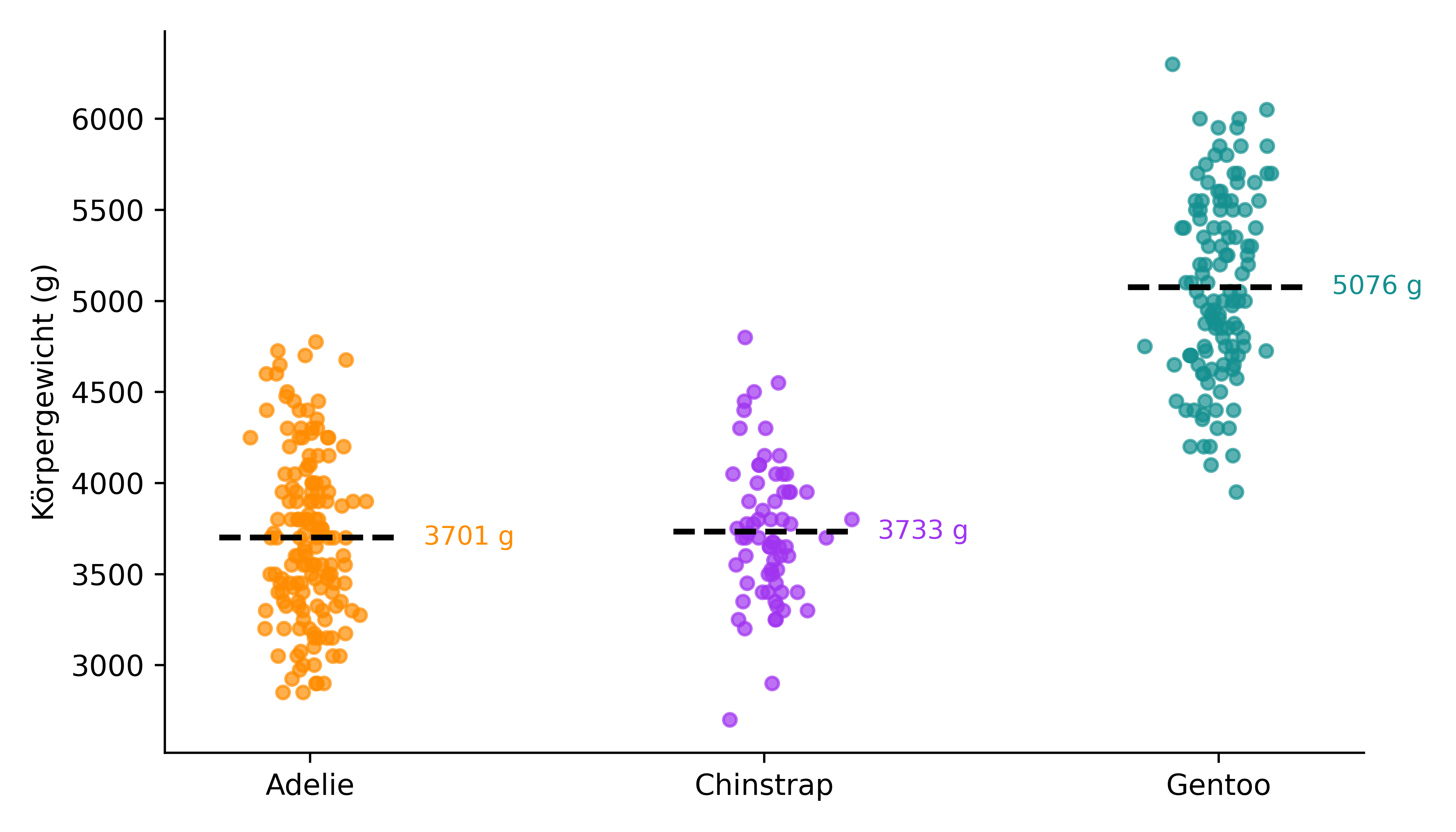
Ein naiver Ansatz wäre, alle Arten paarweise mit t-Tests zu vergleichen. Für drei Arten bräuchten wir drei t-Tests:
- Adelie vs. Chinstrap
- Adelie vs. Gentoo
- Chinstrap vs. Gentoo
# Deskriptive Statistik mit groupby erstellen
desc_stats = penguins.dropna(subset=['body_mass_g']).groupby('species')['body_mass_g'].agg([
('Anzahl', 'count'),
('Mittelwert', 'mean'),
('Std.abw.', 'std')
])
# Formatierung der Zahlen für bessere Lesbarkeit
desc_stats['Mittelwert'] = desc_stats['Mittelwert'].round(2)
desc_stats['Std.abw.'] = desc_stats['Std.abw.'].round(2)
# Tabelle anzeigen
print("Deskriptive Statistik des Körpergewichts (g) nach Pinguinart:")
print(desc_stats)Deskriptive Statistik des Körpergewichts (g) nach Pinguinart:
Anzahl Mittelwert Std.abw.
species
Adelie 151 3700.66 458.57
Chinstrap 68 3733.09 384.34
Gentoo 123 5076.02 504.12Nun führen wir die drei paarweisen t-Tests durch (wir verwenden den Welch-Test):
# Die drei Pinguingruppen extrahieren
adelie = penguins[penguins['species'] == 'Adelie']['body_mass_g'].dropna()
chinstrap = penguins[penguins['species'] == 'Chinstrap']['body_mass_g'].dropna()
gentoo = penguins[penguins['species'] == 'Gentoo']['body_mass_g'].dropna()
# t-Tests zwischen je zwei Arten
t_adelie_chinstrap, p_adelie_chinstrap = stats.ttest_ind(adelie, chinstrap, equal_var=False)
t_adelie_gentoo, p_adelie_gentoo = stats.ttest_ind(adelie, gentoo, equal_var=False)
t_chinstrap_gentoo, p_chinstrap_gentoo = stats.ttest_ind(chinstrap, gentoo, equal_var=False)
# Ergebnisse ausgeben
print("1. Adelie vs. Chinstrap:")
print(f" t-Statistik: {t_adelie_chinstrap:.4f}, p-Wert: {p_adelie_chinstrap:.4f}")
if p_adelie_chinstrap < 0.05:
print(" Signifikanter Unterschied (p < 0.05)")
else:
print(" Kein signifikanter Unterschied")
print("\n2. Adelie vs. Gentoo:")
print(f" t-Statistik: {t_adelie_gentoo:.4f}, p-Wert: {p_adelie_gentoo}")
if p_adelie_gentoo < 0.05:
print(" Signifikanter Unterschied (p < 0.05)")
else:
print(" Kein signifikanter Unterschied")
print("\n3. Chinstrap vs. Gentoo:")
print(f" t-Statistik: {t_chinstrap_gentoo:.4f}, p-Wert: {p_chinstrap_gentoo}")
if p_chinstrap_gentoo < 0.05:
print(" Signifikanter Unterschied (p < 0.05)")
else:
print(" Kein signifikanter Unterschied")1. Adelie vs. Chinstrap:
t-Statistik: -0.5431, p-Wert: 0.5879
Kein signifikanter Unterschied
2. Adelie vs. Gentoo:
t-Statistik: -23.3860, p-Wert: 7.709823145147335e-65
Signifikanter Unterschied (p < 0.05)
3. Chinstrap vs. Gentoo:
t-Statistik: -20.6278, p-Wert: 3.413963146026216e-48
Signifikanter Unterschied (p < 0.05)Diese Ergebnisse zeigen, dass es statistisch signifikante Unterschiede zwischen Adelie und Gentoo sowie zwischen Chinstrap und Gentoo gibt, aber nicht zwischen Adelie und Chinstrap. Doch es gibt ein grundsätzliches Problem mit diesem Ansatz: die Alpha-Fehler-Kumulierung.
Was genau ist nochmal der Alpha-Fehler?
Jeder statistische Hypothesentest hat eine gewisse Wahrscheinlichkeit, einen Fehler zu machen. Diese Wahrscheinlichkeit kann niemals auf 0 reduziert werden, ist also immer da. Diese Fehler werden in zwei Kategorien unterteilt: \(\alpha\)-Fehler (Typ-I-Fehler) und \(\beta\)-Fehler (Typ-II-Fehler).
Im Kontext von statistischen Hypothesentests bezieht sich der Alpha-Fehler (Type I error; auch bekannt als Typ-I-Fehler, Fehler 1. Art, Alpha-Risiko) auf die Wahrscheinlichkeit, die Nullhypothese fälschlicherweise zu verwerfen, obwohl sie tatsächlich wahr ist. Mit anderen Worten: Der \(\alpha\)-Fehler tritt auf, wenn wir einen Unterschied oder Effekt als statistisch signifikant einstufen, obwohl in der Grundgesamtheit kein wirklicher Unterschied oder Effekt existiert. Es ist die Wahrscheinlichkeit, etwas zu “entdecken”, das gar nicht da ist - ein falsch-positives Ergebnis. Bei der üblichen Festlegung eines Signifikanzniveaus von α = 0,05 akzeptieren wir eine 5%-Wahrscheinlichkeit, einen \(\alpha\)-Fehler zu begehen. Das bedeutet, dass wir bei 100 durchgeführten Tests, bei denen die Nullhypothese tatsächlich wahr ist, erwarten würden, dass wir etwa 5-mal fälschlicherweise signifikante Ergebnisse erhalten.
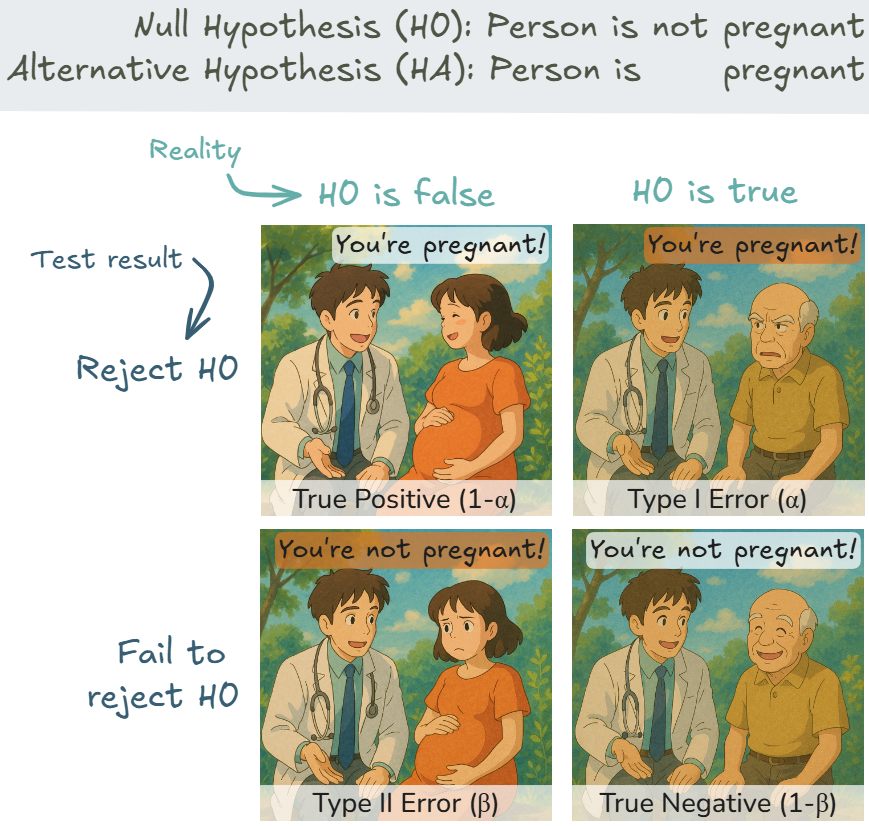
Wie in der Abbildung veranschaulicht, entspricht der \(\alpha\)-Fehler dem Fall, in dem der Test ein positives Ergebnis liefert (“You’re pregnant!”), obwohl die Realität negativ ist (H₀ ist wahr: “Person is not pregnant”). Dies ist der obere rechte Quadrant der Abbildung, gekennzeichnet als “Type I Error (α)”. Der Gegenpol zum \(\alpha\)-Fehler ist der Beta-Fehler (Type II error; auch bekannt als Typ-II-Fehler, Fehler 2. Art, Beta-Risiko), bei dem wir die Nullhypothese nicht verwerfen, obwohl sie falsch ist. In unserem Beispiel entspricht dies dem Fall, in dem der Test ein negatives Ergebnis liefert (“You’re not pregnant!”), obwohl die Person tatsächlich schwanger ist (unterer linker Quadrant).
Wie gesagt sind die Wahrscheinlichkeiten für diese Fehler immer größer als 0. Darüber hinaus gilt, dass wenn man die Wahrscheinlichkeit von einem der beiden Fehler durch entsprechende Maßnahmen reduziert, dass die Wahrscheinlichkeit des anderen steigt.
Alpha-Fehler-Kumulierung
Wie gesagt akzeptieren wir bei jedem statistischen Test diesen Alpha-Fehler und somit ein gewisses Risiko (typischerweise 5%), dass wir die Nullhypothese fälschlicherweise. Das hieße hier bei unserem t-Test im Pinguin-Beispiel, dass wir fälschlicherweise annehmen, dass es einen Unterschied zwischen den Gruppen gibt, obwohl das nicht der Fall ist. Wenn wir mehrere Tests durchführen, gilt natürlich weiterhin für jeden einzelnen Test, dass die Wahrscheinlichkeit, einen Typ-I-Fehler zu begehen, 5% beträgt. Doch die Wahrscheinlichkeit, bei mindestens einem der mehreren Tests einen Typ-I-Fehler zu begehen, steigt mit der Anzahl der Tests.
Die Wahrscheinlichkeit, bei \(m\) Tests mindestens einen Typ-I-Fehler zu begehen, ist:
\[P(\text{mindestens ein Typ-I-Fehler}) = 1 - (1 - \alpha)^m\]
Bei drei Tests mit \(\alpha = 0.05\) ist diese Wahrscheinlichkeit:
\[P(\text{mindestens ein Typ-I-Fehler}) = 1 - (1 - 0.05)^3 = 1 - 0.95^3 \approx 0.143\]
Also etwa 14,3% statt der gewünschten 5%! Dieses Problem verschärft sich mit zunehmender Anzahl an Tests schnell. Hätten wir beispielsweise 4 Pinguinarte, so müssten wir bereits 6 Tests durchführen um jede mit jeder anderen zu vergleichen und die Wahrscheinlichkeit, dass mindestens einer der Tests einen Typ-I-Fehler produziert, wäre:
\[1 - (1 - 0.05)^{6} \approx 0.265\]
also 26,5%! Aber nochmal, damit es klar ist: Dieses Problem trat im letzten Kapitel nicht auf, da wir stets nur einen t-Test durchgeführt haben und dabei verschiedene Versionen des Tests (z.B. Welch-Test, gepaarter Test) betrachtet haben. Hier geht es nun darum, dass wir denselben t-Test mehrfach durchführen würden, um mehrere Hypothesen quasi gleichzeitig zu testen. Die einzelnen Tests wissen aber sozusagen nichts voneinander, sondern funktionieren isoliert. Das ist multiple Testproblem.
Korrekturverfahren für multiple Tests
Um das Problem der Alpha-Fehler-Kumulierung zu adressieren, wurden verschiedene Korrekturverfahren entwickelt. Eine der ersten und bekanntesten ist der Tukey-Test (auch Tukey HSD Test, für “Honestly Significant Difference”), der 1949 von John Tukey entwickelt wurde. Der Tukey-Test kontrolliert die familienweise Fehlerrate über alle Vergleiche hinweg. Das Wort “familienweise” meint hier, dass wir mehrere Hypothesen testen, die alle miteinander verwandt sind (z.B. alle paarweisen Vergleiche zwischen Gruppen). Er sorgt also dafür, dass der nicht jeder einzelne Test ein Alpha von 5% hat, sondern dass die Wahrscheinlichkeit, mindestens einen Typ-I-Fehler zu begehen, bei 5% bleibt, egal wie viele Tests wir durchführen.
Wenden wir den Tukey-Test auf unsere Pinguindaten an:
from statsmodels.stats.multicomp import pairwise_tukeyhsd
# DataFrame ohne fehlende Werte erstellen
penguins_clean = penguins.dropna(subset=['body_mass_g'])
# Tukey HSD Test durchführen
tukey_results = pairwise_tukeyhsd(
endog=penguins_clean['body_mass_g'], # Abhängige Variable
groups=penguins_clean['species'], # Gruppierungsvariable
alpha=0.05 # Signifikanzniveau
)
print(tukey_results) Multiple Comparison of Means - Tukey HSD, FWER=0.05
==============================================================
group1 group2 meandiff p-adj lower upper reject
--------------------------------------------------------------
Adelie Chinstrap 32.426 0.8807 -126.5002 191.3522 False
Adelie Gentoo 1375.354 0.0 1243.1786 1507.5294 True
Chinstrap Gentoo 1342.928 0.0 1178.481 1507.375 True
--------------------------------------------------------------Wie immer kommt dieser Vorteil (kleinerer Alpha-Fehler über alle Tests hinweg) zu einem Preis: Der Tukey-Test ist weniger sensitiv als die einzelnen t-Tests. Das bedeutet, dass er weniger wahrscheinlich einen Unterschied zwischen den Gruppen findet, wenn es tatsächlich einen gibt. Mit anderen Worten: Die Wahrscheinlichkeit einen Typ-II-Fehler zu begehen (fälschlicherweise die Nullhypothese nicht abzulehnen, wenn sie falsch ist) ist höher als bei den t-Tests. Dies ist ein typisches Beispiel für den Kompromiss zwischen Typ-I-Fehler und Typ-II-Fehler (fälschlicherweise die Nullhypothese abzulehnen, wenn sie wahr ist) - man kann nicht beides gleichzeitig minimieren.
Neben dem Tukey-Test existieren weitere Korrekturverfahren:
Bonferroni-Korrektur (
statsmodels.stats.multitest.multipletests(method='bonferroni')): Teilt das Signifikanzniveau durch die Anzahl der Tests – einfach, aber oft zu konservativ.Holm-Methode (
statsmodels.stats.multitest.multipletests(method='holm')): Eine schrittweise Verfeinerung der Bonferroni-Methode, die p-Werte der Größe nach sortiert und weniger konservativ ist.Dunnett-Test (
scipy.stats.dunnett()): Spezialisiert auf Vergleiche zwischen einer Kontrollgruppe und mehreren Behandlungsgruppen. Eine direkte Implementierung in statsmodels gibt es nicht; stattdessen kann die Methode in neueren Versionen von scipy verwendet werden.Scheffé-Test: Ermöglicht den Vergleich beliebiger linearer Kombinationen von Gruppenmittelwerten und ist besonders konservativ. Es gibt keine direkte Implementation in
statsmodels; externe Bibliotheken wie scikit-posthocs bieten jedoch entsprechende Funktionen (z.B.posthoc_scheffe()).False Discovery Rate (FDR) (
statsmodels.stats.multitest.multipletests(method='fdr_bh')): Kontrolliert den erwarteten Anteil falscher Entdeckungen und ist weniger konservativ als die familienweise Fehlerratenkontrolle.
Die Wahl des Korrekturverfahrens hängt von der spezifischen Fragestellung und dem Kontext ab. Für allgemeine paarweise Vergleiche nach einer ANOVA ist der Tukey-Test oft die beste Wahl, da er einen guten Kompromiss zwischen Kontrolle des Alpha-Fehlers und statistischer Power bietet.
Doch anstatt einzelne t-Tests mit Korrekturen durchzuführen, können wir auch eine Varianzanalyse (ANOVA) verwenden, da diese von Anfang an für Vergleiche zwischen mehreren Gruppen konzipiert ist.
Lineare Modelle mit kategoriellen Variablen
Bisher haben wir lineare Modelle hauptsächlich mit numerischen unabhängigen Variablen betrachtet. Doch was passiert, wenn unsere unabhängige Variable kategoriell ist, wie in unserem Fall die Pinguinart? Das geht natürlich auch.
t-Test als Spezialfall eines linearen Modells
Um diesen Zusammenhang zu verstehen, betrachten wir zunächst, wie ein t-Test für zwei unabhängige Stichproben als lineares Modell ausgedrückt werden kann. Nehmen wir wieder den Vergleich zwischen Adelie und Gentoo. Wir können eine neue Spalte is_gentoo erzeugen, die immer eine 1 enthält, wenn die Species Gentoo ist und sonst eine 0. Solch eine Spalte nennt man auch Dummy-Variable.
# Datensatz mit nur Adelie und Gentoo erstellen
adelie_gentoo = penguins[penguins['species'].isin(['Adelie', 'Gentoo'])].copy()
# Dummy-Variable erstellen: 1 für Gentoo, 0 für Adelie
adelie_gentoo['is_gentoo'] = (adelie_gentoo['species'] == 'Gentoo').astype(int)
print(adelie_gentoo) rowid species island ... sex year is_gentoo
0 1 Adelie Torgersen ... male 2007 0
1 2 Adelie Torgersen ... female 2007 0
2 3 Adelie Torgersen ... female 2007 0
3 4 Adelie Torgersen ... NaN 2007 0
4 5 Adelie Torgersen ... female 2007 0
.. ... ... ... ... ... ... ...
271 272 Gentoo Biscoe ... NaN 2009 1
272 273 Gentoo Biscoe ... female 2009 1
273 274 Gentoo Biscoe ... male 2009 1
274 275 Gentoo Biscoe ... female 2009 1
275 276 Gentoo Biscoe ... male 2009 1
[276 rows x 10 columns]Dann passen wir ein lineares Modell an, bei dem diese Dummy-Variable unsere einzige unabhängige Variable ist. Es ist also prinzipiell wie eine einfache lineare Regression (Kapitel 3.5) \(y=a+bx\), allerdings gibt es für x ausschließlich die Werte 0 und 1. Was nun passiert ist etwas abstrakt, aber alle Körpergewichte der einen Pinguinart (Adelie) liegen bei x=0 und alle der anderen (Gentoo) bei x=1. Mehr Werte gibt es nicht. Die Gerade der linearen Regression wird dann also so geschätzt, dass sie möglichst optimal durch die Punkte der beiden Gruppen verläuft. Nutzt man dann das geschätzte Modell um das Körpergewicht der Adelie-Pringuine vorherzusagen, gilt \(\hat{y}_{Adelie} = a\), weil \(x\) ja dann 0 ist und durch die Multiplikation mit der Steigung \(b\) diese komplett wegfällt. Die Modellvorhersage für Adelie entspricht also dem Achsenabschnitt \(a\). Für Gentoo gilt dann \(\hat{y}_{Gentoo} = a + b\), weil \(x\) ja dann 1 ist und die Steigung \(b\) dann einfach addiert wird. Das bedeutet, dass der Achsenabschnitt \(a\) dem Mittelwert der Körpergewichte der Adelie-Pinguine entspricht und die Steigung \(b\) dem Unterschied zwischen den beiden Gruppen.
# Lineares Modell mit der Dummy-Variable
model_t_test = smf.ols(formula='body_mass_g ~ is_gentoo', data=adelie_gentoo).fit()
print(model_t_test.summary()) OLS Regression Results
==============================================================================
Dep. Variable: body_mass_g R-squared: 0.672
Model: OLS Adj. R-squared: 0.671
Method: Least Squares F-statistic: 557.6
Date: Di, 19 Aug 2025 Prob (F-statistic): 8.03e-68
Time: 11:41:08 Log-Likelihood: -2079.1
No. Observations: 274 AIC: 4162.
Df Residuals: 272 BIC: 4169.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 3700.6623 39.024 94.831 0.000 3623.835 3777.489
is_gentoo 1375.3540 58.244 23.614 0.000 1260.687 1490.021
==============================================================================
Omnibus: 11.373 Durbin-Watson: 3.052
Prob(Omnibus): 0.003 Jarque-Bera (JB): 6.235
Skew: 0.172 Prob(JB): 0.0443
Kurtosis: 2.346 Cond. No. 2.52
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Das Ergebnis zeigt:
- Der Intercept (3700,66) entspricht dem mittleren Körpergewicht der Adelie-Pinguine (Referenzgruppe).
- Der Koeffizient für
is_gentoo(1375,35) ist die Differenz zwischen dem mittleren Gewicht von Gentoo und Adelie. - Der p-Wert für
is_gentooist der p-Wert für den Unterschied - genau wie beim t-Test!
Hier haben wir die kategorielle Variable „Pinguinart” mit nur zwei Ausprägungen durch eine binäre Dummy-Variable kodiert. Das lineare Modell schätzt dann im Wesentlichen die Gruppenmittelwerte, und der Test auf den Koeffizienten ist mathematisch äquivalent zum t-Test. Hier eine Visualisierung dieses Ansatzes:
Code zeigen/verstecken
# Werte direkt aus dem Modell extrahieren
intercept = model_t_test.params['Intercept']
slope = model_t_test.params['is_gentoo']
adelie_mean = intercept
gentoo_mean = intercept + slope
intercept_color = '#ff006e'
slope_color = '#3a86ff'
regline_color = '#8338ec'
# Plot erstellen
fig, ax = plt.subplots(figsize=(8, 6), layout='tight')
# Jitter für Datenpunkte erzeugen
jitter_amt = 0.05
adelie_x = np.zeros(len(adelie)) + np.random.normal(0, jitter_amt, len(adelie))
gentoo_x = np.ones(len(gentoo)) + np.random.normal(0, jitter_amt, len(gentoo))
# Datenpunkte plotten
ax.scatter(adelie_x, adelie, alpha=0.6, color='#FF8C00')
ax.scatter(gentoo_x, gentoo, alpha=0.6, color='#159090')
# Mittelwerte markieren
ax.hlines(y=adelie_mean, xmin=-0.2, xmax=0.2, colors='black', linestyles='--', linewidth=2)
ax.hlines(y=gentoo_mean, xmin=0.8, xmax=1.2, colors='black', linestyles='--', linewidth=2)
# Regressionsgerade
x_extended = [-0.5, 1.5]
y_extended = [adelie_mean - 0.5*slope, gentoo_mean + 0.5*slope]
ax.plot(x_extended, y_extended, color=regline_color, linewidth=2)
# Y-Achsen-Limits setzen
ylim_max = max(gentoo.max(), adelie.max()) * 1.1
ax.set_ylim(0, ylim_max);
# Achsenabschnitt (Intercept) für Adelie
ax.vlines(x=0, ymin=0, ymax=adelie_mean, color=intercept_color, linestyle='-', linewidth=2);
# Achsenabschnitt (Intercept) + Steigung (Slope) für Gentoo
ax.vlines(x=1, ymin=0, ymax=adelie_mean, color=intercept_color, linestyle='-', linewidth=2);
ax.vlines(x=1, ymin=adelie_mean, ymax=gentoo_mean, color=slope_color, linestyle='-', linewidth=2);
ax.text(1.25, adelie_mean/2, f"Achsenabschnitt\n= {adelie_mean:.1f}", ha='left', va='center', color=intercept_color);
ax.text(1.25, adelie_mean + slope/2, f"Steigung\n= {slope:.1f}", ha='left', va='center', color=slope_color);
# Beschriftungen
ax.set_xlabel('Dummy-Variable');
ax.set_ylabel('Körpergewicht (g)');
ax.set_xticks([0, 1]);
ax.set_xticklabels(['0', '1']);
# Referenzlinien ausblenden
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.show()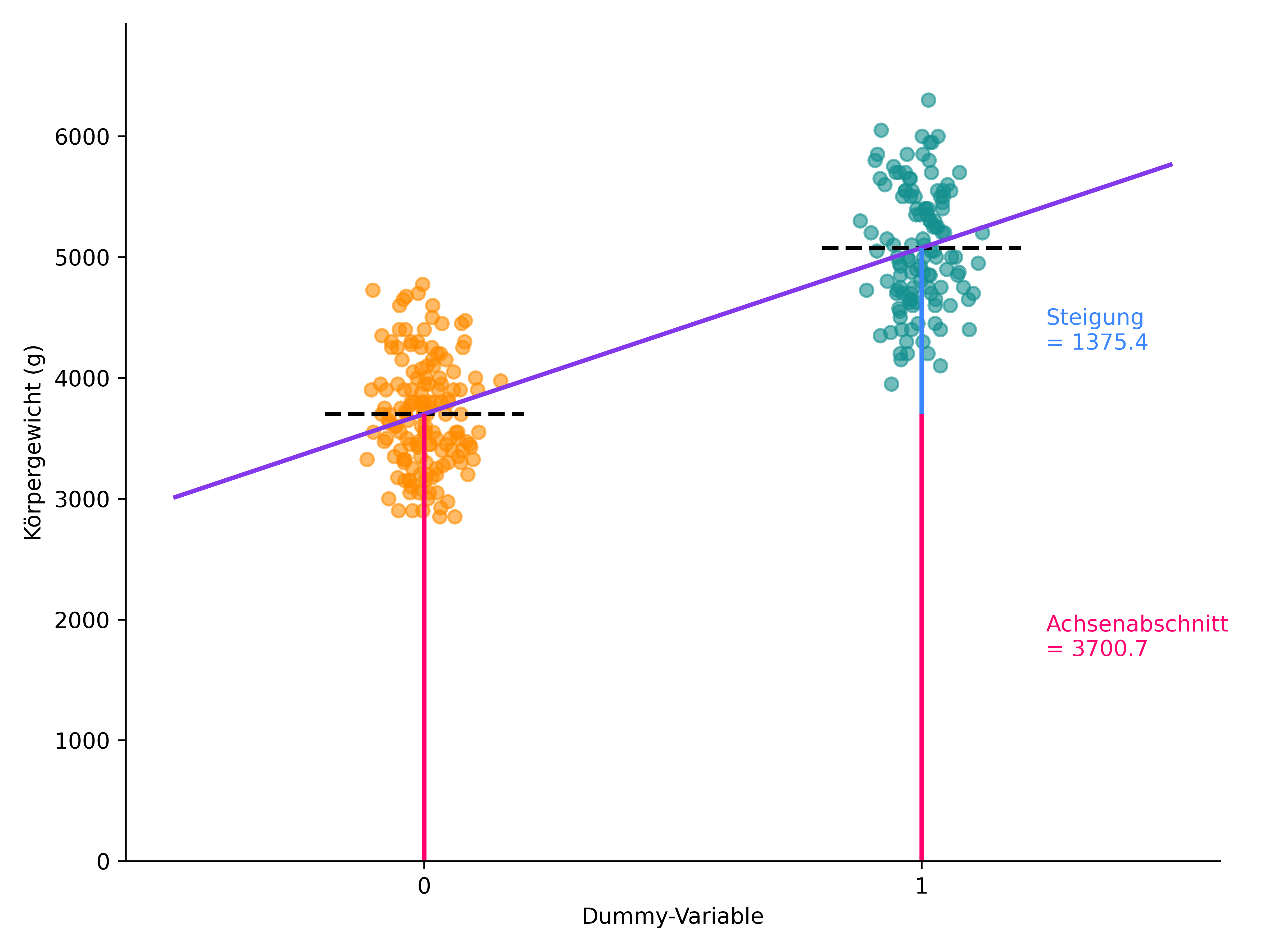
Dummy-Kodierung für kategorielle Variablen
Für kategorielle Variablen mit mehr als zwei Ausprägungen benötigen wir mehrere Dummy-Variablen. Bei \(k\) Kategorien benötigen wir normalerweise \(k-1\) Dummy-Variablen, da eine Kategorie als Referenz dient. Zur Erzeugung dieser Dummy-Variablen können wir die praktische Funktion pd.get_dummies() verwenden. Diese Funktion erstellt für jede Kategorie eine Dummy-Variable. Es sei darauf hingewiesen, dass die Dummy-Variablen hier dann zwar True/False und nicht 1/0 enthalten, was aber kein Problem ist, da Python diese automatisch in 1/0 umwandelt, wenn wir das Modell anpassen (oder andere Berechnungen damit durchführen).
# Mit der Originaltabelle verbinden
penguin_dummies = pd.get_dummies(penguins['species'], drop_first=True)
penguins_with_dummies = pd.concat([penguins, penguin_dummies], axis=1)
print(penguins_with_dummies[['species', 'body_mass_g', 'Chinstrap', 'Gentoo']]) species body_mass_g Chinstrap Gentoo
0 Adelie 3750.0 False False
1 Adelie 3800.0 False False
2 Adelie 3250.0 False False
3 Adelie NaN False False
4 Adelie 3450.0 False False
.. ... ... ... ...
339 Chinstrap 4000.0 True False
340 Chinstrap 3400.0 True False
341 Chinstrap 3775.0 True False
342 Chinstrap 4100.0 True False
343 Chinstrap 3775.0 True False
[344 rows x 4 columns]Hier haben wir mit pd.get_dummies() und der Option drop_first=True zwei Dummy-Variablen erstellt: Chinstrap und Gentoo. Die Referenzkategorie ist Adelie, die implizit durch Chinstrap=0 und Gentoo=0 definiert ist.
Mit dieser Kodierung können wir nun ein lineares Modell erstellen, das die Mittelwerte der drei Pinguinarten modelliert, wobei jede Nicht-Referenzgruppe mit der Referenzgruppe verglichen wird:
# Lineares Modell mit beiden Dummy-Variablen
model_anova = smf.ols(formula='body_mass_g ~ Chinstrap + Gentoo', data=penguins_with_dummies.dropna(subset=['body_mass_g'])).fit()
print(model_anova.summary()) OLS Regression Results
==============================================================================
Dep. Variable: body_mass_g R-squared: 0.670
Model: OLS Adj. R-squared: 0.668
Method: Least Squares F-statistic: 343.6
Date: Di, 19 Aug 2025 Prob (F-statistic): 2.89e-82
Time: 11:41:09 Log-Likelihood: -2582.3
No. Observations: 342 AIC: 5171.
Df Residuals: 339 BIC: 5182.
Df Model: 2
Covariance Type: nonrobust
=====================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------
Intercept 3700.6623 37.619 98.371 0.000 3626.665 3774.659
Chinstrap[T.True] 32.4260 67.512 0.480 0.631 -100.369 165.221
Gentoo[T.True] 1375.3540 56.148 24.495 0.000 1264.912 1485.796
==============================================================================
Omnibus: 7.340 Durbin-Watson: 3.036
Prob(Omnibus): 0.025 Jarque-Bera (JB): 5.331
Skew: 0.182 Prob(JB): 0.0696
Kurtosis: 2.508 Cond. No. 3.45
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Die Interpretation der Ergebnisse:
- Der Intercept (3700,66) entspricht dem mittleren Körpergewicht der Adelie-Pinguine (Referenzgruppe).
- Der Koeffizient für
Chinstrap(32,43) ist der Unterschied zwischen dem mittleren Gewicht von Chinstrap und Adelie. - Der Koeffizient für
Gentoo(1375,35) ist der Unterschied zwischen dem mittleren Gewicht von Gentoo und Adelie.
Wichtig zu beachten ist, dass dieses Modell nicht direkt den Unterschied zwischen Chinstrap und Gentoo testet, sondern nur die Unterschiede zur Referenzkategorie Adelie. Um alle paarweisen Vergleiche zwischen allen Gruppen zu erhalten, benötigen wir zusätzliche Post-hoc-Tests, doch dazu später mehr.
Die p-Werte für die Koeffizienten testen jeweils die Nullhypothese, dass kein Unterschied zur Referenzgruppe besteht. Der p-Wert für den Chinstrap-Koeffizienten (0,631) zeigt, dass dieser Unterschied nicht signifikant ist, während der sehr kleine p-Wert für den Gentoo-Koeffizienten darauf hinweist, dass dieser Unterschied hochsignifikant ist.
Tatsächlich brauchen wir aber übrigens nicht mal die nützliche pd.get_dummies() Funktion. Statsmodels bietet nämlich auch eine elegantere Syntax, bei der wir die kategorielle Variable direkt im Modell spezifizieren können, ohne manuell Dummy-Variablen erstellen zu müssen:
# Direkter Ansatz mit kategorieller Variable
model_cat = smf.ols(formula='body_mass_g ~ C(species)', data=penguins.dropna(subset=['body_mass_g'])).fit()
print(model_cat.summary()) OLS Regression Results
==============================================================================
Dep. Variable: body_mass_g R-squared: 0.670
Model: OLS Adj. R-squared: 0.668
Method: Least Squares F-statistic: 343.6
Date: Di, 19 Aug 2025 Prob (F-statistic): 2.89e-82
Time: 11:41:09 Log-Likelihood: -2582.3
No. Observations: 342 AIC: 5171.
Df Residuals: 339 BIC: 5182.
Df Model: 2
Covariance Type: nonrobust
===========================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------------
Intercept 3700.6623 37.619 98.371 0.000 3626.665 3774.659
C(species)[T.Chinstrap] 32.4260 67.512 0.480 0.631 -100.369 165.221
C(species)[T.Gentoo] 1375.3540 56.148 24.495 0.000 1264.912 1485.796
==============================================================================
Omnibus: 7.340 Durbin-Watson: 3.036
Prob(Omnibus): 0.025 Jarque-Bera (JB): 5.331
Skew: 0.182 Prob(JB): 0.0696
Kurtosis: 2.508 Cond. No. 3.45
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Das Ergebnis ist identisch zum vorherigen Modell: Die Koeffizienten für C(species)[T.Chinstrap] und C(species)[T.Gentoo] entsprechen den Unterschieden zwischen den jeweiligen Arten und der Referenzart (Adelie). Der Präfix C() weist statsmodels an, die Variable als kategoriell zu behandeln, und das [T.] zeigt an, dass es sich um eine “Treatment”-Kodierung handelt, also unsere Dummy-Kodierung.
Selbst die C()-Notation ist nicht zwingend erforderlich, um kategorielle Variablen in statsmodels zu verwenden. Alternativ kann man auch direkt die kategorielle Variable verwenden, wenn sie bereits als Kategorie-Typ definiert ist:
penguins['species'] = penguins['species'].astype('category')
model = smf.ols('body_mass_g ~ species', data=penguins).fit()Der Vorteil C()-Notation ist jedoch zum Einen, dass man explizit erkennt, dass es sich bei dieser Variable um eine kategoriale Variable handelt. Außerdem bietet sie zusätzliche Flexibilität, da sie verschiedene Kodierungsformen ermöglicht - neben der Standard-Treatment-Kodierung wie wir sie gerade benutzt haben, gibt es auch weitere, die für bestimmte statistische Anwendungen nützlich sein können. Diese erweiterten Kodierungsoptionen werden wir hier aber nicht vertiefen.
Fazit & Einordnung
Gehen wir nun also einen Schritt zurück und fassen zusammen, was wir gerade gelernt haben.
Was wir mit der Dummy-Kodierung kategorischer Variablen gemacht haben, mag zunächst wie ein Trick erscheinen, ist aber tatsächlich die mathematische Brücke zwischen linearen Regressionsmodellen und Varianzanalysen. Obwohl es sich grundlegend anders anfühlt numerische oder kategorielle Variablen zu verwenden, sind die zugrunde liegenden Konzepte und Berechnungen sehr ähnlich. In Matrix-Notation können wir weiterhin beide Ansätze einheitlich darstellen.
Betrachten wir zunächst die Matrix-Notation für unser lineares Modell mit Pinguinarten:
Konkret sieht die Design-Matrix für unser Modell mit den drei Pinguinarten (wobei Adelie die Referenzkategorie ist) so aus:
\[\begin{bmatrix} \text{Gewicht}_1 \\ \text{Gewicht}_2 \\ \text{Gewicht}_3 \\ \text{Gewicht}_4 \\ \vdots \\ \text{Gewicht}_n \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \\ 1 & 0 & 0 \\ \vdots & \vdots & \vdots \\ 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \end{bmatrix} + \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \varepsilon_4 \\ \vdots \\ \varepsilon_n \end{bmatrix}\]
Hierbei enthält die Design-Matrix \(\mathbf{X}\) nur Einsen (für den Intercept) und Nullen oder Einsen für die Dummy-Variablen. Wir sehen direkt, wie für jeden Pinguin die entsprechende Zeile kodiert ist: Für Adelie-Pinguine ist die Zeile [1, 0, 0], für Chinstrap-Pinguine [1, 1, 0] und für Gentoo-Pinguine [1, 0, 1].
Vergleichen wir dies mit der Design-Matrix für ein typisches kontinuierliches Regressionsmodell, z.B. wenn wir das Gewicht der Pinguine als Funktion ihrer Schnabellänge (bill_length_mm) modellieren würden:
\[\begin{bmatrix} \text{Gewicht}_1 \\ \text{Gewicht}_2 \\ \text{Gewicht}_3 \\ \vdots \\ \text{Gewicht}_n \end{bmatrix} = \begin{bmatrix} 1 & 39,1 \\ 1 & 39,5 \\ 1 & 40,3 \\ \vdots & \vdots \\ 1 & 50,2 \end{bmatrix} \begin{bmatrix} \beta_0 \\ \beta_1 \end{bmatrix} + \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \vdots \\ \varepsilon_n \end{bmatrix}\]
Der Unterschied liegt lediglich in der Struktur der Design-Matrix \(\mathbf{X}\):
- Bei einer linearen Regression mit kontinuierlichen Variablen enthält \(\mathbf{X}\) die tatsächlichen Werte der Prädiktoren
- Bei kategoriellen Variablen (wie bei ANOVA) enthält \(\mathbf{X}\) Dummy-Variablen (0 und 1), die die Gruppenzugehörigkeit codieren
In beiden Fällen schätzen wir die Koeffizienten \(\mathbf{\beta}\) mit derselben Methode (OLS):
\[\hat{\mathbf{\beta}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}\]
Die F-Statistik der ANOVA testet im Grunde, ob das Modell mit Gruppenvariablen besser ist als ein Modell ohne Gruppenvariablen - genau wie wir bei der linearen Regression die Signifikanz der Koeffizienten testen.
Was als separate statistische Verfahren erscheinen mag, ist in Wirklichkeit Teil desselben mathematischen Rahmenkonzepts:
- Ein t-Test ist ein lineares Modell mit einer binären Dummy-Variable
- Eine ANOVA ist ein lineares Modell mit k-1 Dummy-Variablen für k Gruppen
- Die Signifikanztests in der ANOVA sind identisch mit den Tests für gemeinsame Signifikanz von Koeffizienten in linearen Modellen
Die Unterschiede liegen hauptsächlich in der Tradition, der Darstellung und der üblichen Anwendung, nicht aber in der zugrundeliegenden Mathematik. Wenn man einmal versteht, dass diese Verfahren alle Teil des Allgemeinen Linearen Modells sind, eröffnet sich ein einheitlicher Blick auf viele statistische Methoden.

ANOVA: Test auf Unterschiede zwischen Gruppen
Während die obigen Modelle uns bereits Einblicke in die paarweisen Unterschiede geben, beantwortet die eigentliche ANOVA eine übergeordnete Frage: “Gibt es überhaupt signifikante Unterschiede zwischen den Gruppen?” Diese Frage können wir beantworten, indem wir eine Varianzanalyse auf Basis unseres linearen Modells von eben durchführen. Die Nullhypothese einer Varianzanalyse ist, dass alle Gruppenmittelwerte gleich sind, also dass es keinen Unterschied zwischen den Gruppen gibt. Die Alternativhypothese besagt, dass mindestens ein Gruppenmittelwert unterschiedlich ist. Genau für unseren Fall gilt
- \(H_0: \mu_{Adelie} = \mu_{Chinstrap} = \mu_{Gentoo}\) (alle Gruppenmittelwerte sind gleich)
- \(H_1:\) Mindestens ein Gruppenmittelwert ist unterschiedlich.
Um genau das zu prüfen vergleicht die ANOVA wie der Name schon sagt die Varianzen. Sie vergleicht die Varianz innerhalb der Gruppen (also die Variation der Körpergewichte innerhalb jeder Pinguinart) mit der Varianz zwischen den Gruppen (also die Variation der Mittelwerte zwischen den Pinguinarten). Genauer gesagt wird die F-Statistik berechnet, indem die mittlere Quadratsumme (Mean Square) zwischen den Gruppen durch die mittlere Quadratsumme innerhalb der Gruppen geteilt wird. Die mittlere Quadratsumme ist einfach die Quadratsumme (Sum of Squares) geteilt durch die Freiheitsgrade (Degrees of Freedom). Am Ende erhalten wir eine Varianzanalyse-Tabelle mit einem einzigen F-Wert und einem p-Wert, für den Faktor species. Wenn der p-Wert kleiner als unser Signifikanzniveau (typischerweise 0,05) ist, lehnen wir die Nullhypothese ab und schließen, dass es signifikante Unterschiede zwischen den Gruppen gibt.
# ANOVA-Tabelle aus dem linearen Modell
anova_table = sm.stats.anova_lm(model_cat, typ=2)
print(anova_table) sum_sq df F PR(>F)
C(species) 1.468642e+08 2.0 343.626275 2.892368e-82
Residual 7.244348e+07 339.0 NaN NaNDie ANOVA-Tabelle zeigt:
-
sum_sq: Die Quadratsummen (Sum of Squares), aufgeteilt in die Variation, die durch die Gruppenzugehörigkeit erklärt wird (
C(species)) und die Residualvariation (unerklärte Variation). - df: Die Freiheitsgrade für jede Quelle der Variation.
- F: Die F-Statistik, die das Verhältnis zwischen der erklärten und der unerklärten Variation darstellt.
- PR(>F): Der p-Wert, der die Wahrscheinlichkeit angibt, eine so extreme F-Statistik zu beobachten, wenn die Nullhypothese wahr ist.
Die ANOVA unterteilt die Gesamtvariation in zwei Komponenten:
- Die Variation zwischen den Gruppen (erklärt durch
C(species)) - Die Variation innerhalb der Gruppen (unerklärt; Residuen)
Die F-Statistik ist der Quotient aus der mittleren Quadratsumme zwischen den Gruppen und der mittleren Quadratsumme innerhalb der Gruppen:
\[F = \frac{\text{MS}_{\text{zwischen Gruppen}}}{\text{MS}_{\text{innerhalb Gruppen}}} = \frac{\text{SS}_{\text{zwischen Gruppen}}/\text{df}_{\text{zwischen}}}{\text{SS}_{\text{innerhalb Gruppen}}/\text{df}_{\text{innerhalb}}}\]
Ein großer F-Wert (und demnach ein kleiner p-Wert) deuten darauf hin, dass die Unterschiede zwischen den Gruppen signifikant sind. In unserem Fall ist der F-Wert sehr groß (332,68) und der p-Wert extrem klein, was auf hochsignifikante Unterschiede zwischen mindestens einigen der Pinguinarten hinweist.
Die ANOVA sagt uns allerdings nur, dass es Unterschiede gibt, nicht welche Gruppen sich genau unterscheiden. Dafür würden wir in einem nächsten Schritt Post-hoc-Tests wie den bereits verwendeten Tukey-Test durchführen. Eine gängige Praxis ist aber eben, dass man zuerst eine ANOVA durchführt und dann, wenn diese signifikant ist, Post-hoc-Tests anwendet, um die spezifischen Unterschiede zwischen den Gruppen zu identifizieren. Aus diesem Grund spricht man überhaupt von Post-hoc-Tests.
Alternative Funktionen
An dieser Stelle soll noch erwähnt werden, dass man diese ANOVA auch mit anderen Funktionen durchführen kann. Die Betonung liegt dabei auf “diese”, da wir hier die ganze Zeit vom einfachsten Fall einer Varianzanalyse sprechen: einer einfaktoriellen ANOVA (“one-way ANOVA”) mit nur einem Faktor (species). Es gibt nämlich auch mehrfaktorielle ANOVAs (z.B. wenn wir auch noch das Geschlecht der Pinguine berücksichtigen wollen).
Beispielsweise lässt sich mit SciPy solch eine einfaktoriellen ANOVA mit der Funktion scipy.stats.f_oneway() durchführen. Diese Funktion erwartet die Daten als separate Arrays für jede Gruppe:
# Einfaktorielle ANOVA mit SciPy
f_statistic, p_value = stats.f_oneway(adelie, chinstrap, gentoo)
print(f"F-Statistik: {f_statistic:.4f}")
print(f"p-Wert: {p_value}")F-Statistik: 343.6263
p-Wert: 2.8923681333772885e-82Der Ansatz ist also etwas einfacher zu verwenden, da wir hier nicht erst ein lineares Modell anpassen müssen. Allerdings ist die Funktion scipy.stats.f_oneway() nicht so flexibel wie die ANOVA-Funktion von statsmodels, da sie z.B. keine anderen Typen von ANOVAs unterstützt. Der von uns genutzte Ansatz mit statsmodels ist also langfristig zu bevorzugen, da er auch für komplexere Modelle geeignet ist.
Zusammenfassung
In diesem Kapitel haben wir gelernt, wie wir Mittelwerte von mehr als zwei Gruppen vergleichen können:
Wir haben das Problem der Alpha-Fehler-Kumulierung bei multiplen t-Tests kennengelernt und verstanden, warum spezielle Korrekturverfahren wie der Tukey-Test notwendig sind.
Wir haben gesehen, wie kategorielle Variablen in linearen Modellen durch Dummy-Kodierung verwendet werden können, und wie ein t-Test als Spezialfall eines linearen Modells interpretiert werden kann.
Wir haben die Varianzanalyse (ANOVA) als eine Methode kennengelernt, um zu testen, ob es signifikante Unterschiede zwischen mehreren Gruppen gibt. Die ANOVA zerlegt die Gesamtvariation in die Variation zwischen den Gruppen und die Variation innerhalb der Gruppen.
Übungen
Übung 1
Betrachte folgende Stichproben von Messwerten für vier verschiedene Gruppen:
- Gruppe A: 12, 15, 17, 19, 21
- Gruppe B: 14, 16, 18, 20, 22
- Gruppe C: 18, 20, 22, 24, 26
- Gruppe D: 10, 12, 14, 16, 18
Berechne die F-Statistik der ANOVA für diese Daten. Wie lautet das Ergebnis?
Übung 2
Ein Forscher untersucht den Einfluss von drei verschiedenen Düngern (A, B und C) auf das Pflanzenwachstum. Er misst die Höhe (in cm) der Pflanzen nach 4 Wochen:
- Dünger A: 25, 28, 24, 23, 27
- Dünger B: 31, 29, 32, 30, 33
- Dünger C: 27, 29, 28, 26, 30
- Welchen statistischen Test sollte der Forscher verwenden, um zu prüfen, ob es signifikante Unterschiede im Pflanzenwachstum gibt?
- Der p-Wert der ANOVA beträgt 0.003. Was bedeutet dieses Ergebnis?
Übung 3
Implementiere folgendes Szenario in Python: Ein Marketing-Team testet drei verschiedene Werbestrategien (A, B und C) in verschiedenen Regionen und misst die Umsatzsteigerung (in Prozent). Die Daten sind:
- Strategie A: 5, 7, 3, 6, 4
- Strategie B: 8, 9, 7, 10, 8
- Strategie C: 6, 8, 5, 7, 6
- Führe eine ANOVA durch, um zu testen, ob es signifikante Unterschiede zwischen den Strategien gibt.
- Falls die ANOVA signifikant ist, führe einen geeigneten Post-hoc-Test durch.
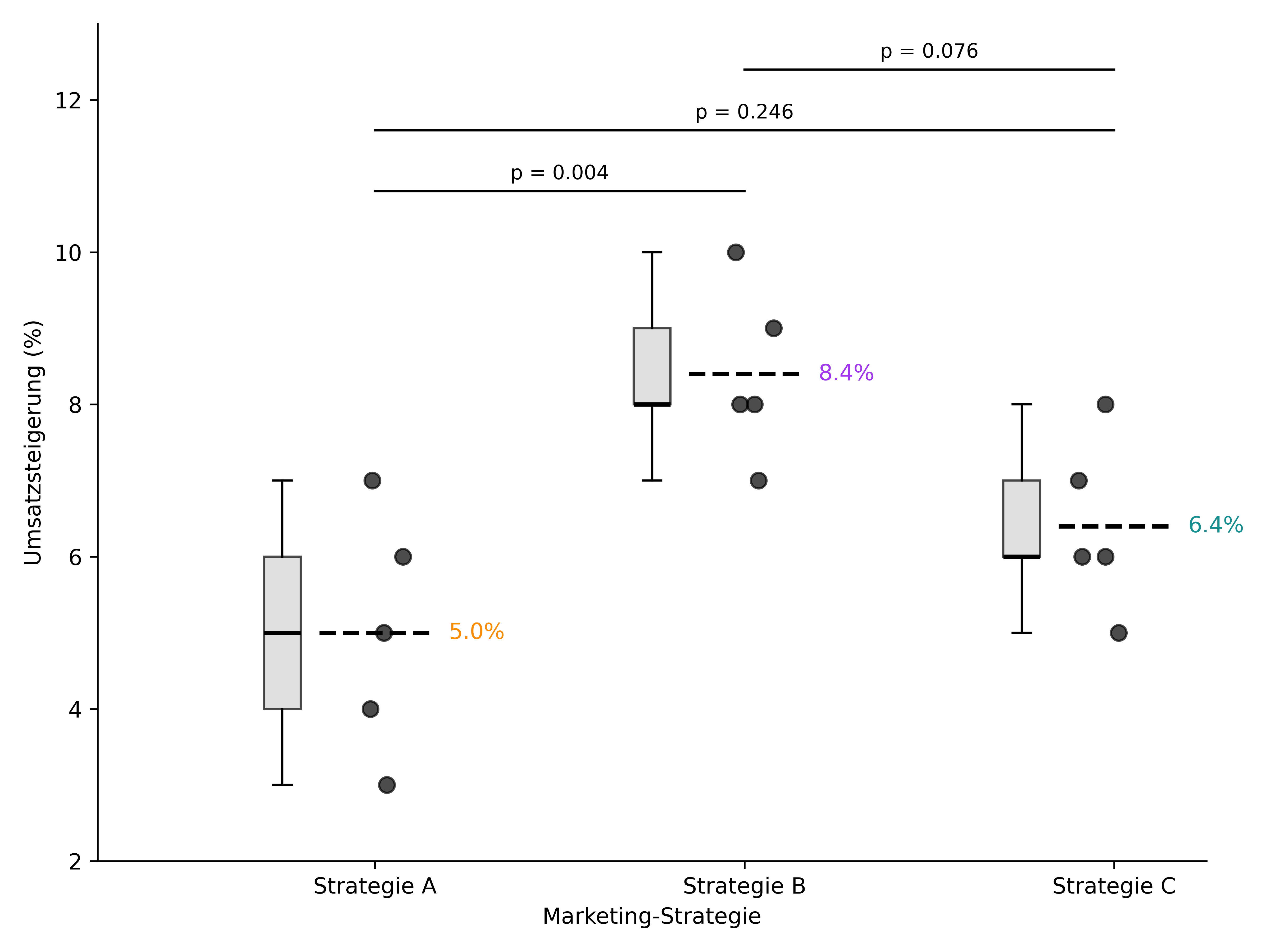
- Visualisiere die Ergebnisse mit einem Boxplot und stelle die p-Werte des Post-hoc-Tests dar.
# Daten für die drei Werbestrategien
strategie_A = np.array([5, 7, 3, 6, 4])
strategie_B = np.array([8, 9, 7, 10, 8])
strategie_C = np.array([6, 8, 5, 7, 6])
# a) DataFrame erstellen für statsmodels
data_marketing = []
for strategie, werte in [('A', strategie_A), ('B', strategie_B), ('C', strategie_C)]:
for wert in werte:
data_marketing.append({'strategie': strategie, 'umsatzsteigerung': wert})
df_marketing = pd.DataFrame(data_marketing)
df_marketing
# Deskriptive Statistik
df_marketing.groupby('strategie')['umsatzsteigerung'].agg([
('Anzahl', 'count'),
('Mittelwert', 'mean'),
('Std.abw.', 'std')
]).round(2)
# a) ANOVA durchführen
model_marketing = smf.ols(formula='umsatzsteigerung ~ C(strategie)', data=df_marketing).fit()
anova_marketing = sm.stats.anova_lm(model_marketing, typ=2)
anova_marketing
f_stat_marketing = anova_marketing.loc['C(strategie)', 'F']
p_val_marketing = anova_marketing.loc['C(strategie)', 'PR(>F)']
# Tukey
tukey_marketing = pairwise_tukeyhsd(
endog=df_marketing['umsatzsteigerung'],
groups=df_marketing['strategie'],
alpha=0.05
)
print(tukey_marketing)
# Abbildung
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
from statsmodels.stats.multicomp import pairwise_tukeyhsd
np.random.seed(42)
# Daten
strategie_A = np.array([5, 7, 3, 6, 4])
strategie_B = np.array([8, 9, 7, 10, 8])
strategie_C = np.array([6, 8, 5, 7, 6])
# DataFrame erstellen
data = []
for strategie, werte in [('A', strategie_A), ('B', strategie_B), ('C', strategie_C)]:
for wert in werte:
data.append({'strategie': strategie, 'umsatz': wert})
df = pd.DataFrame(data)
# Tukey Test
tukey = pairwise_tukeyhsd(df['umsatz'], df['strategie'], alpha=0.05)
tukey_data = tukey.summary().data[1:]
# P-Werte extrahieren
p_vals = {}
for row in tukey_data:
p_vals[f"{row[0]}-{row[1]}"] = float(row[3])
# Plot
fig, ax = plt.subplots(figsize=(8, 6), layout='tight')
colors = {'A': '#FF8C00', 'B': '#A034F0', 'C': '#159090'}
x_pos = {'A': 0, 'B': 1, 'C': 2}
# Boxplots (schmaler und nach links verschoben)
box_data = [df[df['strategie'] == strategie]['umsatz'].values for strategie in ['A', 'B', 'C']]
bp = ax.boxplot(box_data, positions=[-0.25, 0.75, 1.75], widths=0.1, patch_artist=True,
boxprops=dict(facecolor='lightgray', alpha=0.7),
medianprops=dict(color='black', linewidth=2))
# Datenpunkte und Mittelwerte (alle Punkte schwarz)
for strategie in ['A', 'B', 'C']:
data_subset = df[df['strategie'] == strategie]['umsatz']
x_jitter = np.random.normal(x_pos[strategie], 0.05, len(data_subset))
ax.scatter(x_jitter, data_subset, alpha=0.7, s=50, color='black')
# Mittelwert
mean_val = data_subset.mean()
ax.hlines(mean_val, x_pos[strategie]-0.15, x_pos[strategie]+0.15,
colors="black", linestyles='--', linewidth=2)
ax.text(x_pos[strategie]+0.2, mean_val, f"{mean_val:.1f}%",
va='center', ha='left', fontsize=10, color=colors[strategie])
# P-Werte zwischen Gruppen
max_y = df['umsatz'].max()
heights = [max_y + 0.8, max_y + 1.6, max_y + 2.4] # Verschiedene Höhen
comparisons = [('A', 'B', 0), ('A', 'C', 1), ('B', 'C', 2)]
for group1, group2, height_idx in comparisons:
x1, x2 = x_pos[group1], x_pos[group2]
height = heights[height_idx]
p_val = p_vals[f"{group1}-{group2}"]
# Linie
ax.plot([x1, x2], [height, height], linewidth=1, color = 'black')
# P-Wert
p_text = f"p = {p_val:.3f}" if p_val >= 0.001 else "p < 0.001"
ax.text((x1 + x2) / 2, height + 0.1, p_text, ha='center', va='bottom', fontsize=9)
ax.set_ylabel('Umsatzsteigerung (%)')
ax.set_xlabel('Marketing-Strategie')
ax.set_xticks([0, 1, 2])
ax.set_xticklabels(['Strategie A', 'Strategie B', 'Strategie C'])
ax.set_ylim(2, max_y + 3)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
plt.show() strategie umsatzsteigerung
0 A 5
1 A 7
2 A 3
3 A 6
4 A 4
5 B 8
6 B 9
7 B 7
8 B 10
9 B 8
10 C 6
11 C 8
12 C 5
13 C 7
14 C 6
Anzahl Mittelwert Std.abw.
strategie
A 5 5.0 1.58
B 5 8.4 1.14
C 5 6.4 1.14
sum_sq df F PR(>F)
C(strategie) 29.2 2.0 8.588235 0.004841
Residual 20.4 12.0 NaN NaN
Multiple Comparison of Means - Tukey HSD, FWER=0.05
================================================
group1 group2 meandiff p-adj lower upper reject
------------------------------------------------
A B 3.4 0.0037 1.2 5.6 True
A C 1.4 0.2459 -0.8 3.6 False
B C -2.0 0.0762 -4.2 0.2 False
------------------------------------------------
(2.0, 13.0)