import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
from sklearn.linear_model import LinearRegressionMultiple Regression
Im vorherigen Kapitel haben wir die einfache lineare Regression kennengelernt, bei der wir den Zusammenhang zwischen zwei Variablen modelliert haben. In der Praxis werden jedoch komplexe Phänomene selten durch eine einzige Einflussgröße erklärt. Ein Immobilienwert beispielsweise hängt nicht nur von der Anzahl der Räume ab, sondern auch von der Lage, der Größe, dem Baujahr und vielen weiteren Faktoren.
Die multiple lineare Regression ist eine Erweiterung der einfachen linearen Regression, bei der mehrere unabhängige Variablen (Prädiktoren) verwendet werden, um eine abhängige Variable vorherzusagen. Sie ermöglicht es uns, komplexere Zusammenhänge zu modellieren und die Vorhersagegenauigkeit zu verbessern.
Von der einfachen zur multiplen Regression
Erinnern wir uns an das mathematische Modell der einfachen linearen Regression:
\[y = \alpha + \beta x + \varepsilon\]
Bei der multiplen Regression erweitern wir dieses Modell auf mehrere unabhängige Variablen:
\[y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_p x_p + \varepsilon\]
Dabei ist:
- \(y\) die abhängige Variable (das, was wir vorhersagen möchten)
- \(x_1, x_2, \ldots, x_p\) sind die \(p\) verschiedenen unabhängigen Variablen (Prädiktoren)
- \(\beta_0\) ist der Achsenabschnitt (Intercept)
- \(\beta_1, \beta_2, \ldots, \beta_p\) sind die Regressionskoeffizienten für die jeweiligen Prädiktoren
- \(\varepsilon\) ist der Fehlerterm
Beachte, dass wir nun \(\beta_0\) für den Intercept verwenden (statt \(\alpha\) bei der einfachen Regression), um eine konsistente Notation zu haben.
Geometrische Interpretation
Bei der einfachen linearen Regression modellieren wir die Beziehung als eine Gerade in einem zweidimensionalen Raum (eine unabhängige und eine abhängige Variable).
Bei der multiplen Regression mit zwei unabhängigen Variablen modellieren wir eine Ebene in einem dreidimensionalen Raum. Mit mehr als zwei unabhängigen Variablen befindet sich unser Modell in einem mehrdimensionalen Raum und wird als Hyperebene bezeichnet.
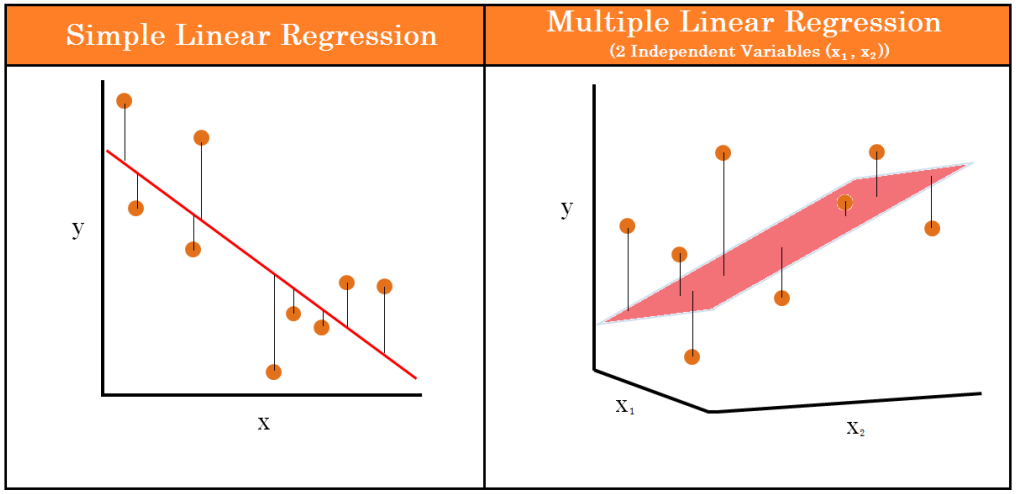
Quelle: Thaddeus Segura
Obwohl wir uns mehr als drei Dimensionen nicht mehr visuell vorstellen können, bleiben die mathematischen Prinzipien dieselben.
Beispieldatensatz: Boston Housing
In diesem Kapitel werden wir mit dem Boston Housing Datensatz arbeiten, der verschiedene Variablen enthält, die den Wert von Immobilien in verschiedenen Stadtteilen von Boston beeinflussen können. Wir konzentrieren uns auf die folgenden Variablen:
# Boston Housing Datensatz laden
pfad = "https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/boston_housing/boston_house_prices.csv"
boston_full = pd.read_csv(pfad, skiprows=1)
# Auf relevante Spalten reduzieren
selected_columns = ['RM', 'LSTAT', 'PTRATIO', 'TAX', 'RAD', 'MEDV']
boston = boston_full[selected_columns].copy()
print(boston) RM LSTAT PTRATIO TAX RAD MEDV
0 6.575 4.98 15.3 296 1 24.0
1 6.421 9.14 17.8 242 2 21.6
2 7.185 4.03 17.8 242 2 34.7
3 6.998 2.94 18.7 222 3 33.4
4 7.147 5.33 18.7 222 3 36.2
.. ... ... ... ... ... ...
501 6.593 9.67 21.0 273 1 22.4
502 6.120 9.08 21.0 273 1 20.6
503 6.976 5.64 21.0 273 1 23.9
504 6.794 6.48 21.0 273 1 22.0
505 6.030 7.88 21.0 273 1 11.9
[506 rows x 6 columns]Die ausgewählten Variablen haben folgende Bedeutungen:
- MEDV: Medianwert der selbstgenutzten Häuser im Stadtteil (in 1.000 US-Dollar). Dies ist unsere Zielvariable, also das, was wir vorhersagen wollen.
- RM: Durchschnittliche Anzahl der Zimmer pro Wohnung/Haus im jeweiligen Gebiet. Mehr Zimmer deuten meist auf größere, komfortablere und teurere Wohnungen hin.
- LSTAT: Prozentsatz der Bevölkerung mit niedrigem sozioökonomischen Status. Ein hoher Wert deutet auf eine ärmere Bevölkerungsschicht hin, was sich oft negativ auf Immobilienpreise auswirkt.
- PTRATIO: Durchschnittliches Schüler-Lehrer-Verhältnis an öffentlichen Schulen im Stadtteil. Ein niedriger Wert steht für kleinere Klassen und potenziell bessere Bildungsbedingungen.
- TAX: Höhe des Grundsteuersatzes pro 10.000 US-Dollar Immobilienwert. Ein hoher Wert bedeutet höhere jährliche Grundsteuerkosten für Hausbesitzer.
- RAD: Index für die Erreichbarkeit von Highways. Ein höherer Wert steht für eine bessere Anbindung an das Schnellstraßennetz, was Pendeln erleichtert, aber auch Lärm und Verkehr mit sich bringen kann.
Visuelle Erkundung der Beziehungen
Lassen wir uns die Beziehungen zwischen jeder der unabhängigen Variablen und dem Immobilienwert (MEDV) ansehen:
fig, axs = plt.subplots(3, 2, figsize=(14, 12))
axs = axs.flatten()
# Liste der unabhängigen Variablen
independent_vars = ['RM', 'LSTAT', 'PTRATIO', 'TAX', 'RAD']
xlabels = ['Anzahl der Räume (RM)',
'Bevölkerung mit niedrigem Status in % (LSTAT)',
'Schüler-Lehrer-Verhältnis (PTRATIO)',
'Grundsteuersatz pro 10.000$ (TAX)',
'Index der Autobahnanbindung (RAD)']
# Plots erstellen
for i, var in enumerate(independent_vars):
axs[i].scatter(boston[var], boston['MEDV'], alpha=0.6)
axs[i].set_xlabel(xlabels[i])
axs[i].set_ylabel('Immobilienwert in 1000$ (MEDV)')
# Letzten Subplot ausblenden
fig.delaxes(axs[5])
plt.tight_layout()
plt.show()
Aus diesen Visualisierungen können wir sehen:
- RM (Anzahl der Räume) hat eine starke positive Beziehung mit dem Immobilienwert: mehr Räume = höherer Wert.
- LSTAT (niedrigerer sozioökonomischer Status) hat eine starke negative Beziehung: höherer Anteil an niedrigem Status = niedrigerer Wert.
- PTRATIO (Schüler-Lehrer-Verhältnis) zeigt eine negative Korrelation: mehr Schüler pro Lehrer = niedrigerer Wert.
- TAX und RAD scheinen ebenfalls negativ mit dem Immobilienwert korreliert zu sein, aber die Beziehung ist weniger klar.
Wie schon gesagt kommt prinzipiell mit jeder zusätzlichen unabhängigen Variablen eine zusätzliche Dimension hinzu. Das bedeutet, dass wir bei mehr als zwei unabhängigen Variablen nicht mehr in der Lage sind, die Beziehung zwischen den Variablen visuell darzustellen. Wir können jedoch immer noch die Beziehung zwischen zwei unabhängigen Variablen und der abhängigen Variable als 3D-Plot visualisieren. 3D-Plots sind nicht wirklich gängig, da sie - zumindest ohne Interaktivität - schwer zu lesen bzw. interpretieren sind. Nichtsdestotrotz soll hier zumindest einmalig gezeigt werden, dass matplotlib auch 3D-Plots erstellen kann. Wir verwenden hier die Variablen RM und LSTAT als Prädiktoren für MEDV:
# 3D-Plot erstellen
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
# Datenpunkte plotten
ax.scatter(boston['RM'], boston['LSTAT'], boston['MEDV'],
c='blue', marker='o', alpha=0.6)
# Achsenbeschriftungen
ax.set_xlabel('Anzahl der Räume (RM)')
ax.set_ylabel('Bevölkerung mit niedrigem Status (LSTAT)')
ax.set_zlabel('Immobilienwert (MEDV)')
# Blickwinkel anpassen
ax.view_init(elev=30, azim=45)
plt.tight_layout()
plt.show()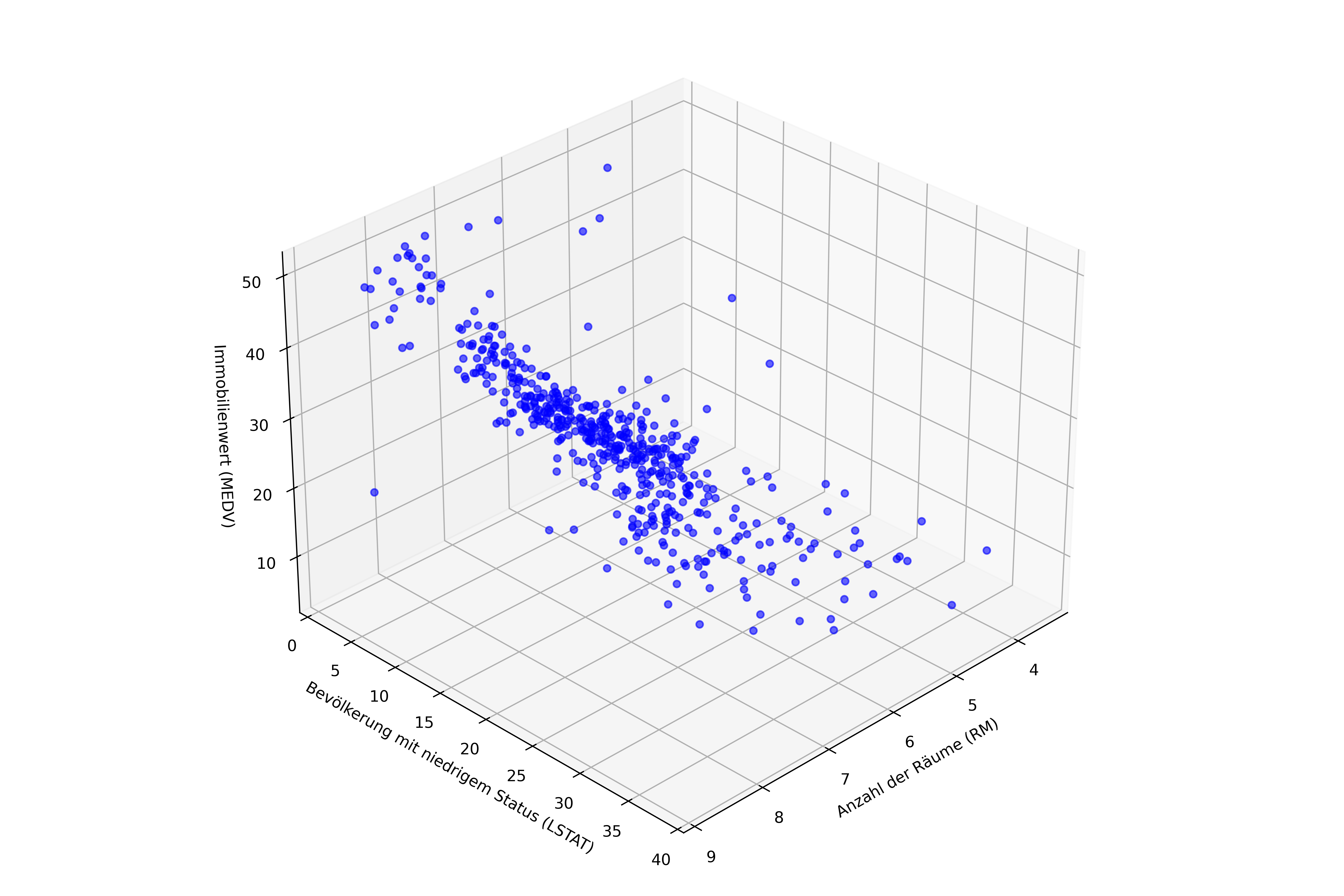
In diesem 3D-Plot können wir die räumliche Verteilung der Datenpunkte sehen. Jeder blaue Punkt repräsentiert eine Immobilie im Datensatz, positioniert entsprechend ihrer Raumanzahl (RM) auf der x-Achse, dem Prozentsatz der Bevölkerung mit niedrigem Status (LSTAT) auf der y-Achse und dem Immobilienwert (MEDV) auf der z-Achse. Wenn wir ein Modell mit diesen beiden Prädiktoren erstellen, würde es geometrisch einer Ebene im dreidimensionalen Raum entsprechen, die versucht, die Punktwolke bestmöglich anzunähern.
Implementierung in Python
Multiple Regression mit scikit-learn
Wir beginnen mit einem Modell, das die beiden Variablen RM und LSTAT als Prädiktoren verwendet:
# Daten vorbereiten
X = boston[['RM', 'LSTAT']] # Unabhängige Variablen
y = boston['MEDV'] # Abhängige Variable
# Modell mit scikit-learn
mod_sklearn = LinearRegression().fit(X, y)
# Koeffizienten ausgeben
print(f"Intercept (β₀): {mod_sklearn .intercept_:.4f}")
print(f"Koeffizient für RM (β₁): {mod_sklearn .coef_[0]:.4f}")
print(f"Koeffizient für LSTAT (β₂): {mod_sklearn .coef_[1]:.4f}")Intercept (β₀): -1.3583
Koeffizient für RM (β₁): 5.0948
Koeffizient für LSTAT (β₂): -0.6424Multiple Regression mit statsmodels
Mit statsmodels können wir eine ausführlichere statistische Analyse durchführen:
# Modell mit statsmodels
mod_statsmodel = smf.ols(formula='MEDV ~ RM + LSTAT', data=boston).fit()
# Koeffizienten ausgeben
print(f"Intercept (β₀): {mod_statsmodel.params[0]:.4f}")
print(f"Koeffizient für RM (β₁): {mod_statsmodel.params[1]:.4f}")
print(f"Koeffizient für LSTAT (β₂): {mod_statsmodel.params[2]:.4f}")Intercept (β₀): -1.3583
Koeffizient für RM (β₁): 5.0948
Koeffizient für LSTAT (β₂): -0.6424Unser Modell lautet also:
\[\text{MEDV} = -1,358 + 5,095 \times \text{RM} - 0,642 \times \text{LSTAT}\]
Interpretation von Koeffizienten in der multiplen Regression
Im Gegensatz zur einfachen linearen Regression, wo ein Koeffizient die Gesamtbeziehung zwischen der unabhängigen und der abhängigen Variable beschreibt, haben Koeffizienten in der multiplen Regression eine spezifischere Interpretation:
Ein Koeffizient in der multiplen Regression gibt an, wie sich die abhängige Variable bei einer Änderung der entsprechenden unabhängigen Variable um eine Einheit ändert, während alle anderen unabhängigen Variablen konstant gehalten werden.
Das ist ein wichtiger Unterschied: In der einfachen Regression kann der Effekt einer Variable durch nicht berücksichtigte Faktoren verfälscht sein. In der multiplen Regression versuchen wir, den “reinen” Effekt jeder Variable zu isolieren, indem wir für andere Einflüsse kontrollieren.
Bei der Interpretation der Koeffizienten ist es wichtig, die Einheiten der Variablen zu berücksichtigen. Zum Einen ist die Zielvariable bereits in 1,000 $ angegeben, zum Anderen mag Ein Koeffizient von 5,095 groß erscheinen, aber wenn man bedenkt, dass er den Einfluss einer ganzen zusätzlichen Raums repräsentiert, ist dies durchaus sinnvoll.
Für unser Modell bedeutet es, dass:
- Der erwartete Basiswert einer Immobilie (wenn RM und LSTAT beide 0 wären) etwa -1358 $ beträgt (was in diesem Fall nicht sinnvoll interpretierbar ist, da es keine Wohnungen mit 0 Räumen gibt)
- Jeder zusätzliche Raum den Wert um etwa 5095 $ erhöht
- Jede Erhöhung des Anteils der Bevölkerung mit niedrigem Status um einen Prozentpunkt den Wert um etwa 642 $ senkt
Modellselektion
Nachdem wir nun ein Modell mit zwei Prädiktoren erstellt haben, stellt sich die Frage: Ist dieses kombinierte Modell tatsächlich besser als Modelle mit nur einem Prädiktor? Oder anders gefragt: Lohnt es sich überhaupt, beide Variablen in das Modell aufzunehmen?
Um diese Frage zu beantworten, vergleichen wir drei verschiedene Modelle hinsichtlich ihres Bestimmtheitsmaßes (R²), das angibt, wie gut die unabhängigen Variablen die Variation der abhängigen Variable erklären. Wir betrachten:
- Ein Modell nur mit RM als Prädiktor
- Ein Modell nur mit LSTAT als Prädiktor
- Das kombinierte Modell mit RM und LSTAT als Prädiktoren
# Drei verschiedene Modelle erstellen
model_rm = smf.ols(formula='MEDV ~ RM', data=boston).fit()
model_lstat = smf.ols(formula='MEDV ~ LSTAT', data=boston).fit()
mod_2var = smf.ols(formula='MEDV ~ RM + LSTAT', data=boston).fit()
# Ausgabe der Bestimmtheitsmaße (R²)
print(f"R² für Modell nur mit RM: {model_rm.rsquared:.4f}")
print(f"R² für Modell nur mit LSTAT: {model_lstat.rsquared:.4f}")
print(f"R² für kombiniertes Modell (RM + LSTAT): {mod_2var.rsquared:.4f}")R² für Modell nur mit RM: 0.4835
R² für Modell nur mit LSTAT: 0.5441
R² für kombiniertes Modell (RM + LSTAT): 0.6386Die Ergebnisse zeigen, dass das kombinierte Modell mit RM und LSTAT ein deutlich höheres R² aufweist als die beiden Einzelmodelle. Dies deutet darauf hin, dass beide Variablen wertvolle und sich ergänzende Informationen zur Vorhersage des Immobilienwerts beitragen. Allerdings hat das einfache R² einen entscheidenden Nachteil:
Das einfache R² steigt immer an, wenn wir weitere Prädiktoren zum Modell hinzufügen, selbst wenn diese nur sehr wenig zur Erklärung der abhängigen Variable beitragen.
Um diesem Problem zu begegnen, gibt es verschiedene andere Informationskriterien, die die Modellkomplexität berücksichtigen.
Adjustiertes R2
Das adjustierte R² (auch: korrigiertes R²) berücksichtigt die Anzahl der Prädiktoren im Modell und bestraft Modelle mit vielen Variablen:
\[R^2_{adj} = 1 - \left(\frac{n-1}{n-p-1}\right) \cdot (1 - R^2)\]
wobei \(n\) die Anzahl der Beobachtungen und \(p\) die Anzahl der Prädiktoren ist.
AIC und BIC
Das Akaike Information Criterion (AIC) und das Bayesian Information Criterion (BIC) sind fortgeschrittenere Maße, die sowohl die Anpassungsgüte als auch die Modellkomplexität berücksichtigen:
\[AIC = -2 \ln(L) + 2k\] \[BIC = -2 \ln(L) + k \ln(n)\]
wobei \(L\) die maximierte Likelihood-Funktion1 des Modells, \(k\) die Anzahl der geschätzten Parameter und \(n\) die Anzahl der Beobachtungen ist.
Bei diesen beiden Kriterien gilt: Je niedriger der Wert, desto besser das Modell. BIC bestraft die Anzahl der Parameter stärker als AIC und bevorzugt daher tendenziell sparsamere Modelle.
Vergleichen wir unsere drei Modelle anhand dieser Kriterien:
# Modellvergleich
model_comparison = pd.DataFrame({
'R²': [model_rm.rsquared, model_lstat.rsquared, mod_2var.rsquared],
'Adj. R²': [model_rm.rsquared_adj, model_lstat.rsquared_adj, mod_2var.rsquared_adj],
'AIC': [model_rm.aic, model_lstat.aic, mod_2var.aic],
'BIC': [model_rm.bic, model_lstat.bic, mod_2var.bic]
}, index=['RM', 'LSTAT', 'RM + LSTAT'])
print(model_comparison) R² Adj. R² AIC BIC
RM 0.483525 0.482501 3350.151117 3358.604191
LSTAT 0.544146 0.543242 3286.974957 3295.428030
RM + LSTAT 0.638562 0.637124 3171.542314 3184.221924Die Ergebnisse zeigen eindeutig, dass das kombinierte Modell in allen Kriterien besser abschneidet als die Einzelmodelle:
- Es hat das höchste R² und adjustierte R²
- Es hat die niedrigsten AIC- und BIC-Werte
Dies bestätigt, dass die Aufnahme beider Variablen (RM und LSTAT) in das Modell zu einer substantiellen Verbesserung führt, die die zusätzliche Komplexität rechtfertigt.
Modellerweiterung
Nachdem wir festgestellt haben, dass das kombinierte Modell mit RM und LSTAT besser ist als die Einzelmodelle, können wir überlegen, ob eine weitere Variable das Modell weiter verbessern könnte. Laut unserer vorherigen Analyse ist PTRATIO (Schüler-Lehrer-Verhältnis) eine weitere Variable mit starker (negativer) Korrelation zum Immobilienwert. Versuchen wir, sie in unser Modell aufzunehmen:
# Erweitertes Modell mit drei Prädiktoren
mod_3var = smf.ols(formula='MEDV ~ RM + LSTAT + PTRATIO', data=boston).fit()
# Zusammenfassung ausgeben
print(mod_3var.summary()) OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.679
Model: OLS Adj. R-squared: 0.677
Method: Least Squares F-statistic: 353.3
Date: Di, 19 Aug 2025 Prob (F-statistic): 2.69e-123
Time: 11:43:41 Log-Likelihood: -1553.0
No. Observations: 506 AIC: 3114.
Df Residuals: 502 BIC: 3131.
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 18.5671 3.913 4.745 0.000 10.879 26.255
RM 4.5154 0.426 10.603 0.000 3.679 5.352
LSTAT -0.5718 0.042 -13.540 0.000 -0.655 -0.489
PTRATIO -0.9307 0.118 -7.911 0.000 -1.162 -0.700
==============================================================================
Omnibus: 202.072 Durbin-Watson: 0.901
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1022.153
Skew: 1.700 Prob(JB): 1.10e-222
Kurtosis: 9.076 Cond. No. 402.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Auch hier sind sich das adj. R², AIC und BIC einig: Das Hinzufügen von PTRATIO hat zu einer weiteren substantiellen Verbesserung des Modells geführt, die die zusätzliche Komplexität rechtfertigt. In der Übung dieses Kapitels wwerden wir aber auch Fälle erleben, in die Hinzunahme einer weiteren Variablen nicht zu einer Verbesserung des Modells führt.
Multikollinearität
In der multiplen Regression müssen wir ein wichtiges Problem berücksichtigen, das in der einfachen Regression nicht auftritt: Multikollinearität. Dies tritt auf, wenn unabhängige Variablen stark miteinander korreliert sind.
Multikollinearität kann verschiedene Probleme verursachen:
- Die Koeffizienten können instabil werden und sich stark ändern, wenn kleine Änderungen am Modell oder an den Daten vorgenommen werden.
- Die Standardfehler der Koeffizienten werden größer, was die statistische Signifikanz verringert.
- Es wird schwieriger, den individuellen Einfluss jeder unabhängigen Variable zu bestimmen.
Stellen wir uns vor, wir möchten ein Modell erstellen, das die Gesamtzahl der Tore vorhersagt, die eine Fußballmannschaft am Ende eines Spiels (nach 90 Minuten) erzielt. Als Prädiktoren haben wir verschiedene Variablen wie den Marktwert der Spieler, Heimvorteil und die Anzahl an bisherigen Saisonsiegen. Dazu kommen zwei besondere Variablen:
- Tore_45min: Die Anzahl der Tore, die die Mannschaft nach 45 Minuten (Halbzeit) erzielt hat
- Tore_50min: Die Anzahl der Tore nach 50 Minuten Spielzeit
Diese beiden Variablen enthalten fast dieselbe Information - sie werden nur dann unterschiedlich sein, wenn genau in diesen 5 Minuten ein Tor fällt. In allen anderen Fällen sind sie identisch.
Wenn wir beide Variablen in unser Modell aufnehmen, tritt Multikollinearität auf. Das Modell kann dann nicht klar erkennen, welche der beiden Variablen tatsächlich wichtiger für die Vorhersage ist. Für uns Menschen ist natürlich klar, dass Tore_50min wahrscheinlich ein leicht besserer Prädiktor ist (da er zeitlich näher am Endergebnis liegt), aber das Modell erkennt diesen Zusammenhang nicht.
Erkennung von Multikollinearität
Korrelationsmatrix
Ein erster Schritt zur Erkennung von Multikollinearität ist die Betrachtung der Korrelationen zwischen den unabhängigen Variablen:
# Korrelationsmatrix nur für die Prädiktoren
predictors = ['RM', 'LSTAT', 'PTRATIO', 'TAX', 'RAD']
corr_matrix = boston[predictors].corr()
# Heatmap der Korrelationsmatrix
fig, ax = plt.subplots(figsize=(10, 8))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', ax=ax)
ax.set_title('Korrelationsmatrix der Prädiktoren')
plt.show()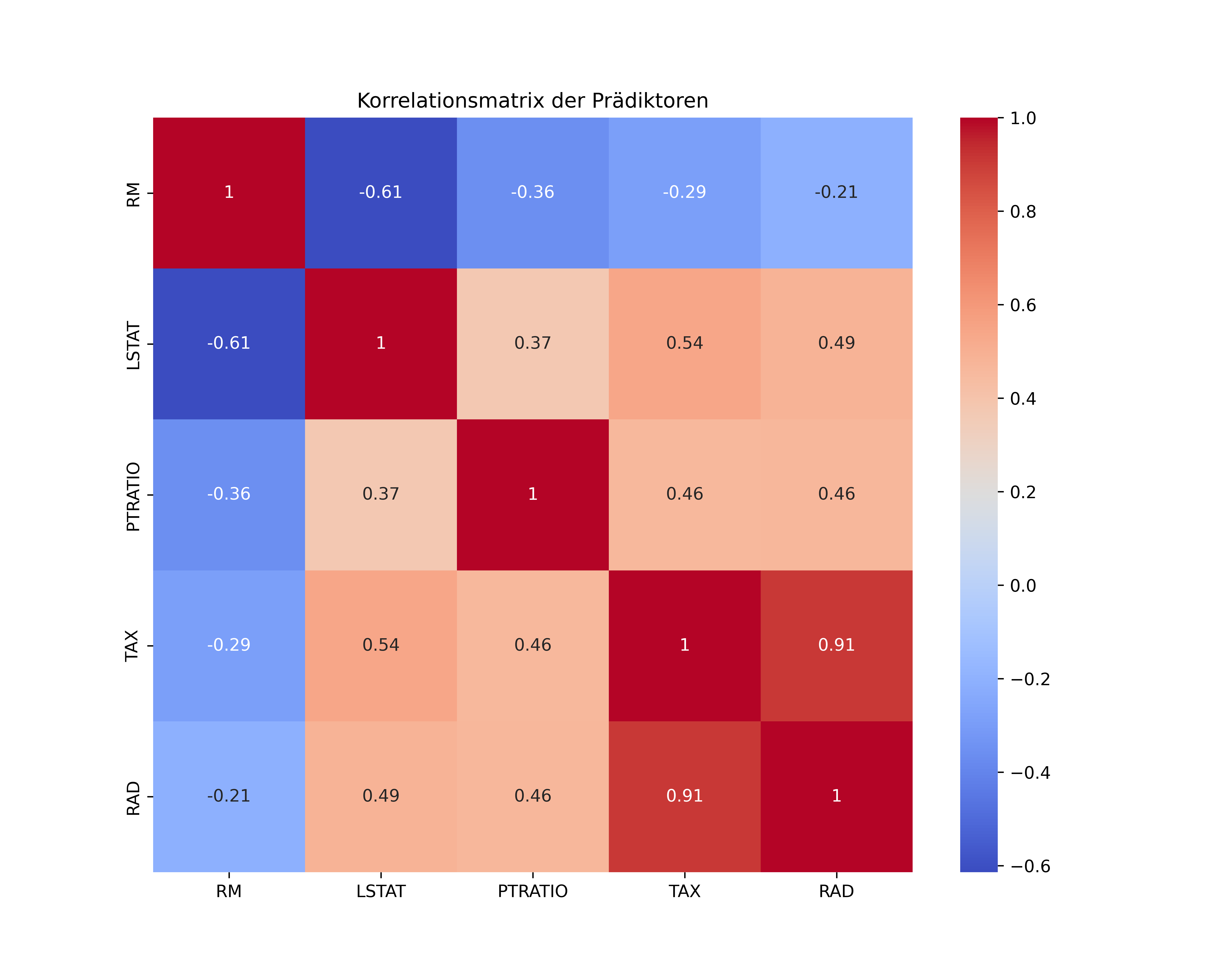
Die Heatmap und die Ausgabe zeigen uns, dass es eine besonders starke Korrelation zwischen TAX und RAD gibt. Wenn zwei Prädiktoren stark korreliert sind kann dies auf Multikollinearität hindeuten. Was stark in diesem Kontext bedeutet hängt davon ab, wen man fragt - Grenzwerte ab wann eine solche Korrelation zu hoch ist liegen in der Regel bei 0,8-0,9.
Variance Inflation Factor (VIF)
Der Varianzinflationsfaktor (VIF) ist eine präzisere Methode zur Quantifizierung von Multikollinearität, da er direkt im Kontext des angepassten Modells berechnet werden kann. Man berechnet für jeden Prädiktor im Modell je einen VIF. Dieser gibt dann jeweils an, wie stark die Varianz seines Regressionskoeffizienten durch Multikollinearität “aufgebläht” wird.
Die Berechnung des VIF erfolgt in zwei Schritten:
- Für jeden Prädiktor \(X_j\) wird ein eigenes Regressionsmodell erstellt, in dem dieser Prädiktor als abhängige Variable und alle anderen Prädiktoren als unabhängige Variablen dienen. Zum Beispiel bei einem Modell mit drei Prädiktoren \(y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3\) würden wir folgende “Hilfsmodelle” berechnen:
- \(X_1 = \gamma_0 + \gamma_2 X_2 + \gamma_3 X_3\)
- \(X_2 = \delta_0 + \delta_1 X_1 + \delta_3 X_3\)
- \(X_3 = \eta_0 + \eta_1 X_1 + \eta_2 X_2\)
- Aus dem Bestimmtheitsmaß \(R^2\) dieser Hilfsmodelle wird dann jeweils der VIF berechnet: \[ \text{VIF}_j = \frac{1}{1 - R^2_j} \]
Wenn ein Prädiktor stark durch die anderen Prädiktoren erklärt werden kann (hohes \(R^2\) im Hilfsmodell), dann ist sein VIF hoch. Das bedeutet, dieser Prädiktor ist redundant, da er größtenteils Informationen enthält, die bereits durch die anderen Prädiktoren abgedeckt sind.
Die Interpretation des VIF ist wie folgt:
- VIF = 1: Keine Multikollinearität - der Prädiktor ist nicht mit den anderen korreliert
- 1 < VIF < 5: Moderate Multikollinearität - oft noch akzeptabel
- 5 < VIF < 10: Hohe Multikollinearität - potenziell problematisch
- VIF > 10: Sehr hohe Multikollinearität - deutet auf ein ernsthaftes Problem hin
Berechnen wir den VIF für unser erweitertes Modell mit RM, LSTAT und PTRATIO:
from statsmodels.stats.outliers_influence import variance_inflation_factor
X = sm.add_constant(boston[['RM', 'LSTAT', 'PTRATIO']])
vif_data = pd.DataFrame()
vif_data["Variable"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
vif_data Variable VIF
0 const 283.342604
1 RM 1.653419
2 LSTAT 1.679425
3 PTRATIO 1.198101Die VIF-Werte für unsere drei Prädiktoren RM, LSTAT, PTRATIO sind alle nur zwischen 1 und 2, was auf eine moderate, aber akzeptable Multikollinearität hindeutet. Die Prädiktoren enthalten also jeweils ausreichend einzigartige Informationen, die nicht durch die anderen Prädiktoren abgedeckt werden.
Zum Vergleich nehmen wir nun noch die beiden stark korrelierten Prädiktoren TAX und RAD in unser Modell auf und berechnen den VIF erneut:
X2 = sm.add_constant(boston[['RM', 'LSTAT', 'PTRATIO', 'TAX', 'RAD']])
vif_multicol = pd.DataFrame()
vif_multicol["Variable"] = X2.columns
vif_multicol["VIF"] = [variance_inflation_factor(X2.values, i) for i in range(X2.shape[1])]
vif_multicol Variable VIF
0 const 337.187389
1 RM 1.744837
2 LSTAT 2.105087
3 PTRATIO 1.401291
4 TAX 6.390041
5 RAD 6.154180Hier sehen wir deutlich höhere VIF-Werte, zumindest für die Prädiktoren TAX und RAD selbst. Diese Werte überschreiten den kritischen Schwellenwert von 5 und nähern sich oder überschreiten sogar 10, was auf eine starke Multikollinearität hinweist. Dies bestätigt unsere Beobachtung aus der Korrelationsmatrix, dass TAX und RAD stark miteinander korreliert sind.
In einem solchen Fall müssten wir erwägen, einen der beiden Prädiktoren aus dem Modell zu entfernen oder andere Techniken zur Behandlung von Multikollinearität anzuwenden.
Auswirkungen der Multikollinearität
Starke Korrelationen zwischen Prädiktoren können verschiedene problematische Auswirkungen auf das Regressionsmodell haben:
- Instabile Koeffizienten
- Die kollinearen Variablen “konkurrieren” um Einfluss im Modell, sodass kleine Änderungen im Datensatz zu großen Änderungen in den geschätzten Koeffizienten führen.
- Die Koeffizienten werden also extrem empfindlich gegenüber Datenänderungen.
- Erhöhte Standardfehler
- Die Standardfehler der Koeffizienten werden größer
- Dies führt zu breiteren Konfidenzintervallen
- Die Präzision der Schätzungen nimmt also ab.
- Irreführende p-Werte
- Als direkte Folge der erhöhten Standardfehler können die p-Werte irreführend sein
- Variablen, die eigentlich einen bedeutenden Einfluss haben, können als nicht signifikant erscheinen
- Statistische Tests verlieren an Teststärke
- Schwierigkeiten bei der Variablenwichtigkeit
- Es wird schwer zu bestimmen, welche der korrelierenden Variablen tatsächlich wichtig ist
- Die Erklärungskraft wird auf die korrelierenden Variablen “aufgeteilt”
- Die individuelle Bedeutung einzelner Prädiktoren wird verschleiert
- Unzuverlässige Vorhersagen
- Das Modell kann trotz hohem R² instabil sein
- Innerhalb der Datenspanne funktionieren Vorhersagen vielleicht gut
- Extrapolationen außerhalb des Datenbereichs werden jedoch unzuverlässiger
Handhabung von Multikollinearität
Es gibt verschiedene Strategien, um mit dem Problem der Multikollinearität umzugehen:
- Variablenselektion
- Entfernung einer oder mehrerer der stark korrelierten Variablen
- Kriterien für die Auswahl:
- Variable mit dem höheren VIF-Wert entfernen
- Variable beibehalten, die stärker mit der Zielvariable korreliert
- Theoretisches Vorwissen für die Entscheidung nutzen
- Modellvergleiche mit AIC, BIC oder adjustiertem R² durchführen
- Regularisierungsmethoden
-
Ridge Regression: Fügt einen Strafterm für die Summe der quadrierten Koeffizienten hinzu
- Verkleinert alle Koeffizienten etwas, behält aber alle Variablen bei
- Besonders nützlich, wenn alle Variablen theoretisch relevant sind
-
Lasso Regression: Fügt einen Strafterm für die Summe der absoluten Koeffizienten hinzu
- Kann einige Koeffizienten genau auf Null setzen
- Führt automatisch eine Variablenselektion durch
- Dimensionsreduktion
- Hauptkomponentenanalyse (PCA) oder Faktoranalyse durchführen
- Die korrelierten Originalvariablen werden zu unkorrelierten Komponenten zusammengefasst
- Diese neuen Komponenten können als Prädiktoren verwendet werden
- Nachteil: Interpretierbarkeit der Ergebnisse kann leiden
- Erhöhung der Stichprobengröße
- Mit mehr Daten können die Standardfehler reduziert werden
- Die Schätzungen werden präziser und stabiler
- Nicht immer praktikabel, aber eine effektive Lösung wenn möglich
- Fachliche Beurteilung
- Nicht jede Entscheidung sollte rein auf statistischen Kriterien basieren
- Manchmal ist es sinnvoll, korrelierte Variablen aus inhaltlichen Gründen beizubehalten
- In diesem Fall sollte man sich der statistischen Einschränkungen bewusst sein
- Die betroffenen Koeffizienten vorsichtig interpretieren
Vorhersagen mit dem multiplen Regressionsmodell
Prinzipiell können wir mit dem multiplen Regressionsmodell genau so Vorhersagen treffen wie schon mit dem einfachen Regressionsmodell. Der einzige Unterschied ist, dass wir jetzt mehrere Prädiktoren haben. Das bedeutet, dass wir auch mehrere Werte, also einen für jede unabhängige Variable, angeben müssen. Ebenso können wir auch hier Vorhersagen für genau die Beobachtungen treffen, die wir im Datensatz haben und so Residuen berechnen.
Wir tun das hier mal sowohl für das mod_2var (mit RM und LSTAT) als auch für das mod_3var (mit RM, LSTAT und PTRATIO).
# Vorhersagen mit beiden Modellen
boston['pred_2var'] = mod_2var.predict(boston)
boston['pred_3var'] = mod_3var.predict(boston)
# Residuen beider Modelle
boston['resid_2var'] = mod_2var.resid
boston['resid_3var'] = mod_3var.resid
boston[['RM', 'LSTAT', 'MEDV', 'pred_2var', 'pred_3var', 'resid_2var', 'resid_3var']] RM LSTAT MEDV pred_2var pred_3var resid_2var resid_3var
0 6.575 4.98 24.0 28.941014 31.168357 -4.941014 -7.168357
1 6.421 9.14 21.6 25.484206 25.767464 -3.884206 -4.167464
2 7.185 4.03 34.7 32.659075 32.139173 2.040925 2.560827
3 6.998 2.94 33.4 32.406520 31.080407 0.993480 2.319593
4 7.147 5.33 36.2 31.630407 30.386589 4.569593 5.813411
.. ... ... ... ... ... ... ...
501 6.593 9.67 22.4 26.020059 23.262747 -3.620059 -0.862747
502 6.120 9.08 20.6 23.989216 21.464318 -3.389216 -0.864318
503 6.976 5.64 23.9 30.560067 27.296530 -6.660067 -3.396530
504 6.794 6.48 22.0 29.093235 25.994407 -7.093235 -3.994407
505 6.030 7.88 11.9 24.301515 21.744097 -12.401515 -9.844097
[506 rows x 7 columns]Bei der einfachen linearen Regression konnten wir die Vorhersagen und Residuen in einem einzigen Diagramm darstellen. Bei der multiplen Regression ist das nicht mehr ohne Weiteres möglich, da wir mehrere Prädiktoren haben.
Streng genommen können wir eine 3D-Version der Abbildung aus dem Kapitel zur einfachen linearen Regression erstellen - zumindest für das Modell mit zwei Prädiktoren. Spätestens hier wird aber deutlich, dass 3D-Visualisierungen schnell an ihre Grenzen kommen:
# 3D-Plot für das Modell mit zwei Variablen erstellen
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
# Datenpunkte plotten
ax.scatter(boston['RM'], boston['LSTAT'], boston['MEDV'],
c='blue', marker='o', alpha=0.6, label='Beobachtungen')
# Modellvorhersage als Ebene darstellen
# Eine Gitter für die Ebene erstellen
x_min, x_max = boston['RM'].min() - 0.5, boston['RM'].max() + 0.5
y_min, y_max = boston['LSTAT'].min() - 0.5, boston['LSTAT'].max() + 0.5
x_grid, y_grid = np.meshgrid(np.linspace(x_min, x_max, 30),
np.linspace(y_min, y_max, 30))
# Koeffizienten aus dem Modell
intercept = mod_2var.params.iloc[0]
beta_rm = mod_2var.params.iloc[1]
beta_lstat = mod_2var.params.iloc[2]
# Vorhergesagte Werte für das Gitter berechnen
z_grid = intercept + beta_rm * x_grid + beta_lstat * y_grid
# Ebene plotten
surf = ax.plot_surface(x_grid, y_grid, z_grid, alpha=0.3, color='green')
# Residuen als rote Linien darstellen
for i in range(len(boston)):
x = boston['RM'].iloc[i]
y = boston['LSTAT'].iloc[i]
z_actual = boston['MEDV'].iloc[i]
z_pred = boston['pred_2var'].iloc[i]
# Linie zwischen tatsächlichem Wert und Vorhersage zeichnen
ax.plot([x, x], [y, y], [z_actual, z_pred], color='red', alpha=0.4)
# Achsenbeschriftungen
ax.set_xlabel('RM')
ax.set_ylabel('LSTAT')
ax.set_zlabel('MEDV')
# Manuelle Legende mit Proxy-Objekten
from matplotlib.lines import Line2D
from matplotlib.patches import Rectangle
legend_elements = [
Line2D([0], [0], marker='o', color='w', markerfacecolor='blue', markersize=10, label='Beobachtungen'),
Line2D([0], [0], color='red', label='Residuen'),
Rectangle((0, 0), 1, 1, fc='green', alpha=0.3, label='Modellvorhersage')
]
ax.legend(handles=legend_elements, loc='upper center', bbox_to_anchor=(0.5, -0.05))
# Blickwinkel anpassen
ax.view_init(elev=30, azim=45)
plt.tight_layout()
plt.show()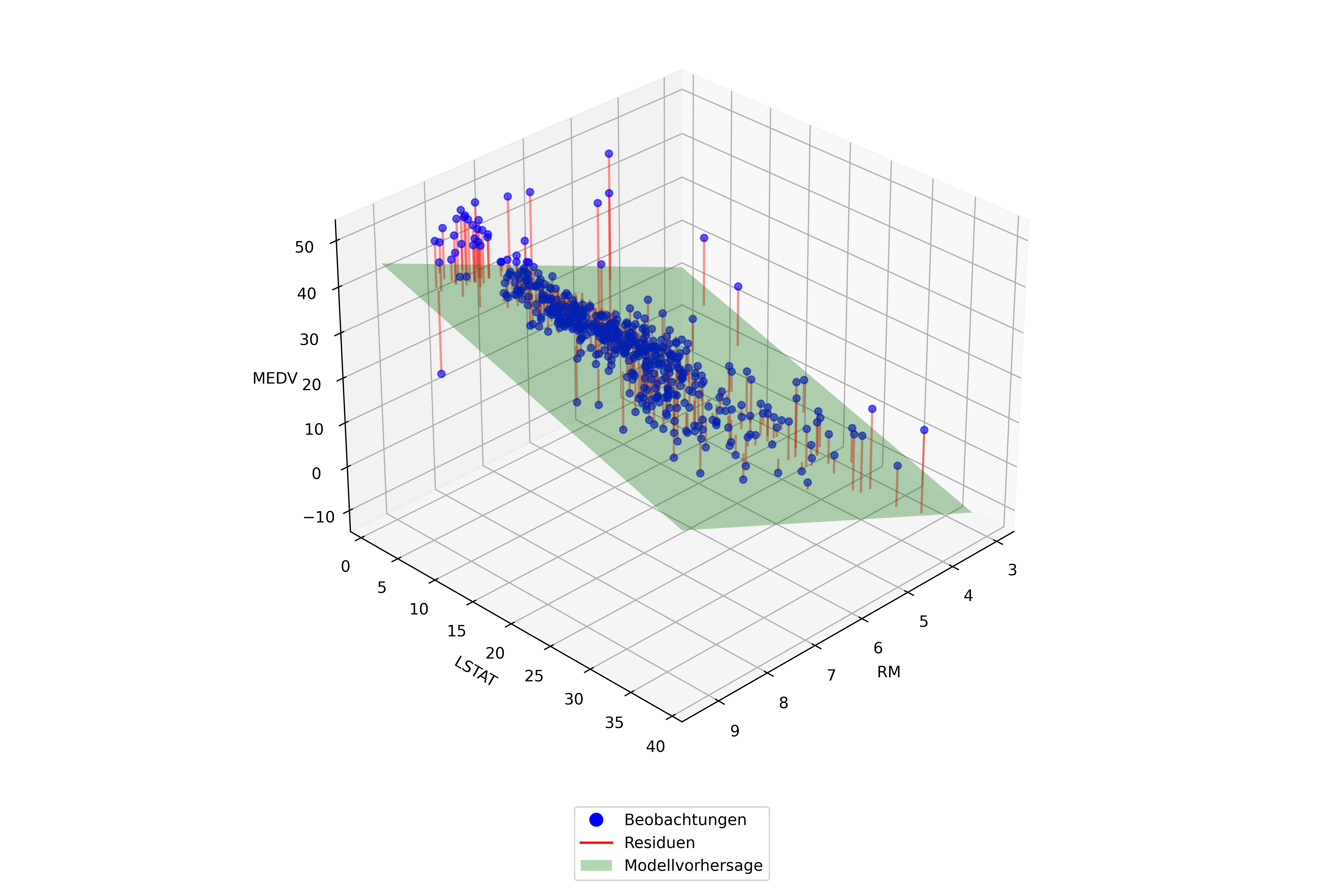
Was wir aber immer tun können ist, die tatsächlichen Werte der abhängigen Variable (MEDV) gegen die vorhergesagten Werte (pred_2var und pred_3var) zu plotten. Auch das gibt uns eine Vorstellung davon, wie gut unser Modell funktioniert.
# Streudiagramm der tatsächlichen vs. vorhergesagten Werte
fig, axs = plt.subplots(1, 2, figsize=(15, 6))
# Modell mit RM und LSTAT
axs[0].scatter(boston['MEDV'], boston['pred_2var'], alpha=0.6)
axs[0].plot([0, 50], [0, 50], 'r--') # Perfekte Vorhersage-Linie
axs[0].set_title('Modell mit RM und LSTAT')
axs[0].set_xlabel('Tatsächliche Werte')
axs[0].set_ylabel('Vorhergesagte Werte')
# Modell mit RM, LSTAT und PTRATIO
axs[1].scatter(boston['MEDV'], boston['pred_3var'], alpha=0.6)
axs[1].plot([0, 50], [0, 50], 'r--') # Perfekte Vorhersage-Linie
axs[1].set_title('Modell mit RM, LSTAT und PTRATIO')
axs[1].set_xlabel('Tatsächliche Werte')
axs[1].set_ylabel('Vorhergesagte Werte')
plt.tight_layout()
plt.show()
# RMSE berechnen
def rmse(y_true, y_pred):
return np.sqrt(np.mean((y_true - y_pred) ** 2))
print(f"RMSE für das Modell mit zwei Variablen: {rmse(boston['MEDV'], boston['pred_2var']):.4f}")
print(f"RMSE für das Modell mit drei Variablen: {rmse(boston['MEDV'], boston['pred_3var']):.4f}")
RMSE für das Modell mit zwei Variablen: 5.5238
RMSE für das Modell mit drei Variablen: 5.2087Die Streudiagramme und RMSE-Werte2 zeigen, dass das erweiterte Modell mit drei Prädiktoren etwas bessere Vorhersagen liefert als das einfache Modell mit zwei Prädiktoren. Dies bestätigt, was wir bereits durch den Vergleich der Informationskriterien festgestellt haben: Die Hinzufügung von PTRATIO als Prädiktor verbessert das Modell.
Zusammenfassung
In diesem Kapitel haben wir die multiple lineare Regression kennengelernt, die eine Erweiterung der einfachen linearen Regression auf mehrere unabhängige Variablen darstellt. Wir haben:
Das mathematische Modell hinter der multiplen Regression verstanden: \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \ldots + \beta_p x_p + \varepsilon\)
-
Die Interpretation von Koeffizienten in der multiplen Regression gelernt:
- Koeffizienten repräsentieren den Effekt einer Variablen, während alle anderen konstant gehalten werden
- Dies unterscheidet sich von der einfachen Regression, wo Effekte durch nicht berücksichtigte Faktoren verfälscht sein können
-
Modellselektion und Informationskriterien betrachtet:
- Einfaches R² kann bei Hinzufügen von Variablen nur steigen
- Adjustiertes R² berücksichtigt die Modellkomplexität
- AIC und BIC helfen bei der Wahl des besten Modells
-
Multikollinearität als spezifisches Problem der multiplen Regression verstanden:
- Entstehung durch starke Korrelationen zwischen Prädiktoren
- Erkennung durch Korrelationsmatrix und Variance Inflation Factor (VIF)
- Auswirkungen: instabile Koeffizienten, erhöhte Standardfehler, irreführende p-Werte
- Lösungsansätze: Variablenselektion, Regularisierung, Dimensionsreduktion
Die multiple Regression ist ein mächtiges Werkzeug, das komplexe Zusammenhänge zwischen mehreren Prädiktoren und einer Zielvariable modellieren kann. Sie bildet die Grundlage für viele fortgeschrittene statistische Verfahren und Machine-Learning-Techniken. Mit den in diesem Kapitel erworbenen Kenntnissen sind wir nun in der Lage, realistischere Modelle zu erstellen, die mehrere Einflussfaktoren berücksichtigen.
Übungen
Übung 1
Schreibe eine Funktion calculate_vifs, die den Variance Inflation Factor (VIF) für alle Spalten eines DataFrames berechnet und als übersichtliche Tabelle zurückgibt. Die Funktion sollte:
- Einen DataFrame mit den Prädiktoren als Input nehmen
- Automatisch die nötige Konstante hinzufügen (für statsmodels; siehe oben)
- Den VIF für jeden Prädiktor berechnen
- Die Ergebnisse als sortierten DataFrame zurückgeben (absteigend nach VIF-Wert)
from statsmodels.stats.outliers_influence import variance_inflation_factor
import statsmodels.api as sm
def calculate_vifs(X):
"""
Berechnet den Variance Inflation Factor für alle Spalten eines DataFrames
Parameters:
-----------
X : pandas.DataFrame
Der DataFrame mit den Prädiktoren
Returns:
--------
pandas.DataFrame
DataFrame mit den VIF-Werten für jeden Prädiktor, absteigend sortiert
"""
# Dein Code hier
return vif_df
# Teste deine Funktion
vif_results = calculate_vifs(boston[['RM', 'LSTAT', 'PTRATIO', 'TAX', 'RAD']])
print(vif_results)Übung 2
In dieser Übung wirst du mit dem bekannten Palmer Penguins Datensatz arbeiten, der Messungen von verschiedenen Pinguinarten enthält. Deine Aufgabe ist es, verschiedene lineare Regressionsmodelle zu erstellen, die die Körpermasse der Pinguine (body_mass_g) vorhersagen, und diese Modelle dann zu vergleichen.
- Lade den Datensatz mit folgendem Code:
import pandas as pd
import statsmodels.formula.api as smf
# Load data
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
df = pd.read_csv(csv_url)-
Erstelle alle möglichen Kombinationen von linearen Regressionsmodellen mit den Prädiktoren
bill_depth_mm,flipper_length_mmundbill_length_mm. Das bedeutet:- Drei Modelle mit jeweils einem Prädiktor
- Drei Modelle mit jeweils zwei Prädiktoren
- Ein Modell mit allen drei Prädiktoren
-
Vergleiche diese Modelle anhand von AIC, BIC und adjustiertem R². Erstelle dazu einen DataFrame, der die folgenden Spalten enthält:
- Die Modellformel
- AIC-Wert
- BIC-Wert
- Adjustiertes R²
Sortiere die Ergebnisse nach jeweils einem der drei Informationskriterien und interpretiere, welches Modell am besten geeignet scheint, die Körpermasse vorherzusagen.
Bonus: Kannst du einen eleganteren Weg finden, alle möglichen Modellkombinationen zu erstellen, anstatt jedes Modell manuell zu definieren? Tipp: Die
itertools-Bibliothek könnte hilfreich sein.
Hinweis: Achte auf die Interpretation der Ergebnisse. Ein höheres adjustiertes R² bedeutet eine bessere Anpassung des Modells an die Daten, während niedrigere AIC- und BIC-Werte auf sparsamere Modelle hindeuten, die dennoch gut erklären.
Fußnoten
Was die Likelihood-Funktion ist, wird in einem späteren Kapitel erklärt. Kurz gesagt, quantifiziert sie die Übereinstimmung zwischen Modell und Beobachtungen. Sie gibt die Wahrscheinlichkeit an, mit der das statistische Modell die beobachteten Daten generieren würde.↩︎
Siehe Loss-Funktionen im vorangegangenen Kapitel↩︎