import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.metrics import accuracy_score, classification_report
from sklearn.preprocessing import LabelEncoder
np.random.seed(42)Ensemble Methoden: Random Forest
In vorangegangenen Kapiteln haben wir Decision Trees kennengelernt - eine mächtige und interpretierbare Methode für Klassifikation und Regression. Aber wie wir gesehen haben, haben einzelne Decision Trees ein fundamentales Problem: Sie sind instabil und neigen zum Overfitting. Kleine Änderungen in den Daten können zu völlig unterschiedlichen Bäumen führen, und ohne Kontrolle können sie zu spezifische Regeln lernen, also welche, die zwar gut zum Trainings- aber eher nicht zum Testdatensatz passen.
Übrigens: Um Overfitting zu quantifizieren, vergleicht man typischerweise die Accuracy auf den Trainingsdaten mit der Accuracy auf den Testdaten. Die Logik dahinter ist intuitiv: Wenn ein Modell die Trainingsdaten deutlich besser vorhersagt als die Testdaten, dann hat es sich vermutlich zu stark an die spezifische Struktur der Trainingsdaten angepasst und generalisiert schlecht. Eine große Lücke zwischen Training- und Test-Accuracy ist also ein klares Warnsignal für Overfitting.
Die “Weisheit der Massen” besagt, dass die kollektive Meinung vieler oft besser ist als die Meinung eines einzelnen Experten - selbst wenn dieser Experte sehr gut ist. Genau dieses Prinzip nutzen Ensemble-Methoden: Anstatt sich auf einen einzelnen Decision Tree zu verlassen, kombinieren sie die Vorhersagen vieler Bäume zu einer robusteren Gesamtentscheidung.
Ein Ensemble kombiniert mehrere schwache Lerner (z.B. einfache Decision Trees) zu einem starken Lerner. Dabei können die einzelnen Modelle sogar schlechter sein als ein komplexer Einzelbaum - aber ihre Kombination ist oft deutlich besser und stabiler.
Die Daten: Adelie vs. Gentoo Pinguine
Für dieses Kapitel konzentrieren wir uns auf eine binäre Klassifikation zwischen Adelie und Gentoo Pinguinen aus dem Palmer Penguins Datensatz. Um den Unterschied zwischen Decision Tree und Random Forest deutlich zu demonstrieren, verwenden wir nur eine reduzierte Feature-Auswahl von body_mass_g und island - dies führt zu einer interessanteren Klassifikationssituation.
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
# Nur Adelie und Gentoo auswählen (beste Kombination für Random Forest Demonstration)
penguins_binary = penguins[penguins['species'].isin(['Adelie', 'Gentoo'])].copy()
# Bewusst reduzierte Feature-Auswahl für interessante Klassifikation
feature_cols = ['body_mass_g', 'island']
penguins_clean = penguins_binary[feature_cols + ['species']].dropna()
# One-Hot-Encoding für 'island' (kategorisch)
penguins_encoded = pd.get_dummies(penguins_clean, columns=['island'], drop_first=True)
# Finale Features (automatisch generierte Dummy-Variablen)
feature_cols_encoded = [col for col in penguins_encoded.columns if col != 'species']
X = penguins_encoded[feature_cols_encoded]
y = penguins_encoded['species']
print(f"Finale Daten: {len(X)} Pinguine mit {len(feature_cols_encoded)} Features")
print(f"Finale Features: {feature_cols_encoded}")Finale Daten: 274 Pinguine mit 3 Features
Finale Features: ['body_mass_g', 'island_Dream', 'island_Torgersen']# Train-Test Split mit Stratifikation
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
# Labels für sklearn-Kompatibilität kodieren
le_species = LabelEncoder()
y_train_encoded = le_species.fit_transform(y_train)
y_test_encoded = le_species.transform(y_test)
# Für einzelne Bäume: numpy arrays vorbereiten (verhindert sklearn warnings)
X_train_np = X_train.values
X_test_np = X_test.values
print(f"Training: {len(X_train)}, Test: {len(X_test)}")Training: 191, Test: 83Kurzer Datencheck: Wie gut trennen die Features?
Bevor wir irgendein Modell anpassen, können wir uns ja zumindest grob etwas mehr vergegenwärtigen wie vielversprechend die einzelnen Features beim Kategorisieren sind:
Code zeigen/verstecken
# Explorative Analyse: Wie gut trennen die Features die beiden Arten?
# Species für Plot kodieren (0 = Adelie, 1 = Gentoo)
species_encoded = y.map({'Adelie': 0, 'Gentoo': 1})
# Plot erstellen - 3 Features nebeneinander
fig, axes = plt.subplots(1, 3, figsize=(12, 4), layout='tight')
for i, x_var in enumerate(feature_cols_encoded):
ax = axes[i]
# Scatterplot mit species-Einfärbung
for species in ['Adelie', 'Gentoo']:
species_mask = y == species
data_x = X[x_var][species_mask]
data_y = species_encoded[species_mask] + np.random.normal(0, 0.05, len(data_x)) # Jitter für bessere Sichtbarkeit
ax.scatter(data_x, data_y,
color=colors[species], label=species, alpha=0.7, s=50)
ax.set_xlabel(x_var)
ax.set_ylabel('Art')
ax.set_yticks([0, 1])
ax.set_yticklabels(['Adelie', 'Gentoo'])
ax.grid(True, alpha=0.3)
# Eine einzige Legende
handles, labels = axes[0].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right', bbox_to_anchor=(0.95, 0.95))
plt.suptitle('Adelie vs Gentoo: Trennbarkeits-Analyse der Features', y=0.98)
plt.show()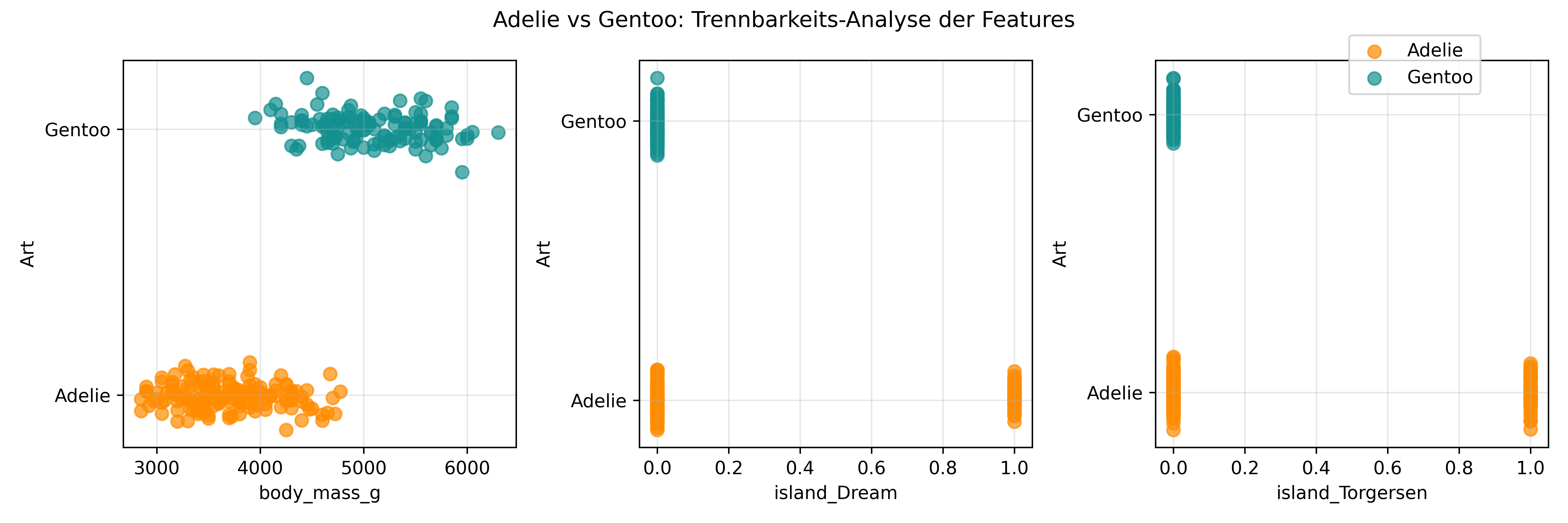
Mit nur wenigen Features sehen wir eine interessante Situation: body_mass_g zeigt eine gewisse Trennung zwischen Adelie und Gentoo Pinguinen, aber die Insel-Information allein ist weniger eindeutig.
Code zeigen/verstecken
# Artenverteilung nach Insel analysieren
island_species = penguins_clean.groupby(['island', 'species']).size().unstack(fill_value=0)
print("Artenverteilung nach Insel:")
print(island_species)
print()
# Prozentuale Verteilung
island_species_pct = island_species.div(island_species.sum(axis=1), axis=0) * 100
print("Prozentuale Verteilung:")
print(island_species_pct.round(1))
print()
# Visualisierung der Insel-Verteilung
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), layout='tight')
# Absolute Zahlen
island_species.plot(kind='bar', ax=ax1, color=[colors['Adelie'], colors['Gentoo']])
ax1.set_title('Absolute Anzahl pro Insel')
ax1.set_xlabel('Insel')
ax1.set_ylabel('Anzahl Pinguine')
ax1.legend(title='Art')
ax1.tick_params(axis='x', rotation=45)
# Prozentuale Verteilung
island_species_pct.plot(kind='bar', ax=ax2, color=[colors['Adelie'], colors['Gentoo']])
ax2.set_title('Prozentuale Verteilung pro Insel')
ax2.set_xlabel('Insel')
ax2.set_ylabel('Prozent')
ax2.legend(title='Art')
ax2.tick_params(axis='x', rotation=45)
plt.show()Artenverteilung nach Insel:
species Adelie Gentoo
island
Biscoe 44 123
Dream 56 0
Torgersen 51 0
Prozentuale Verteilung:
species Adelie Gentoo
island
Biscoe 26.3 73.7
Dream 100.0 0.0
Torgersen 100.0 0.0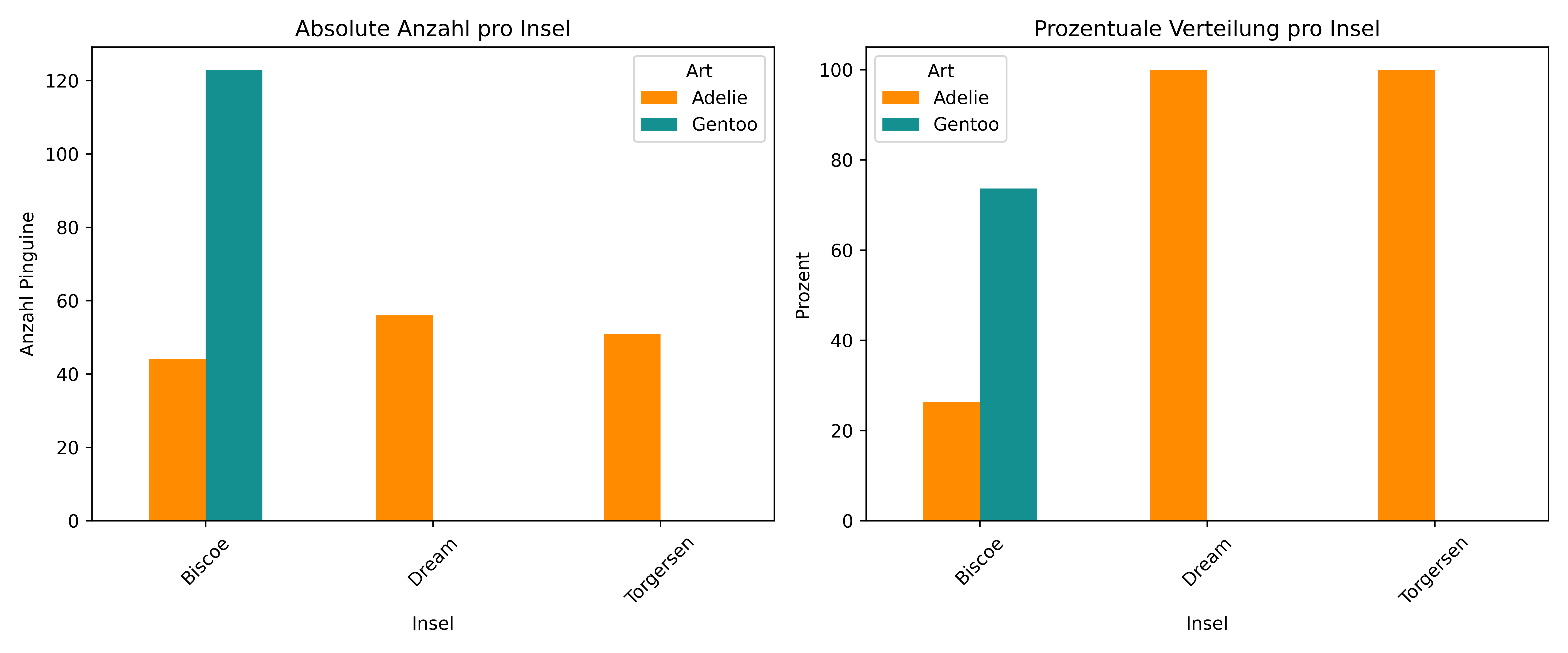
Diese Verteilung zeigt uns, warum die Kombination aus body_mass_g und island eine interessante Klassifikationsaufgabe darstellt - weder Feature allein ist perfekt trennend, aber zusammen können sie möglicherweise gute Ergebnisse liefern.
Übrigens hier eine Karte um wenigstens ein grobes Gefühl für die Lage der drei Orte/Insteln zu bekommen:
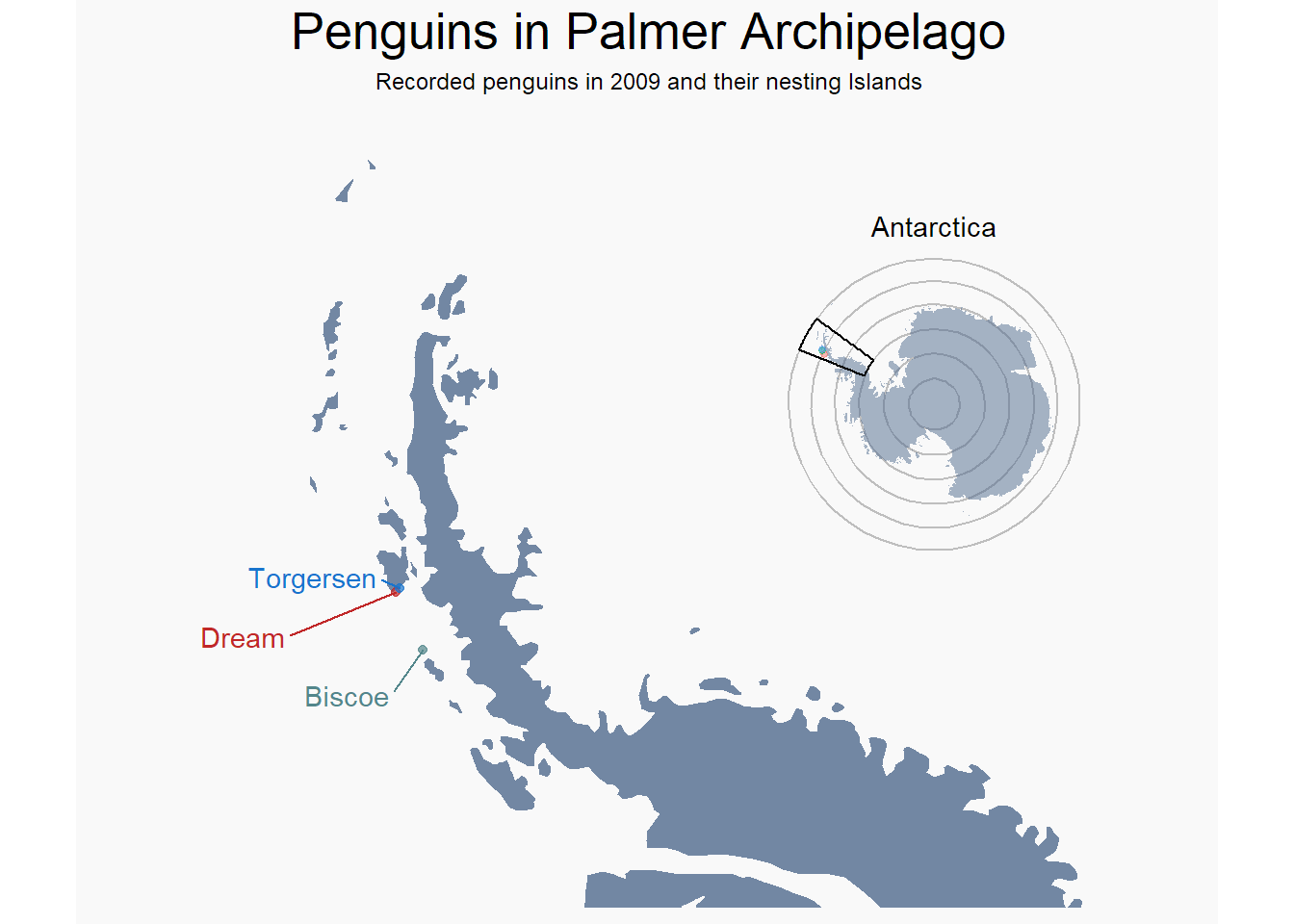
Quelle: Julian Avila-Jimenez
Baseline: Ein einzelner Decision Tree
Bevor wir zu den neuen Ensemble-Methoden übergehen, etablieren wir eine Baseline mit einem einzelnen Decision Tree wie wir ihn schon kennen. Der Übersichtlichkeit halber erlauben wir im gesamten Kapitel mal nur eine maximale Tiefe von 3.
# Einzelner Decision Tree als Baseline
tree_single = DecisionTreeClassifier(max_depth=3, random_state=42)
tree_single.fit(X_train, y_train_encoded);Mit den wenigen Features, einer begrenzten Tiefe und genau diesem Trainingsdatensatz erhalten wir folgenden Decision Tree für die Adelie vs. Gentoo Klassifikation:
Code zeigen/verstecken
# Decision Tree visualisieren
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
plot_tree(tree_single,
feature_names=feature_cols_encoded,
class_names=['Adelie', 'Gentoo'],
filled=True,
rounded=True,
fontsize=11,
ax=ax);
ax.set_title('Einfacher Decision Tree: Adelie vs Gentoo', fontsize=14, pad=20);
plt.show()
# Vorhersagen und Performance
y_pred_train_tree = tree_single.predict(X_train)
y_pred_test_tree = tree_single.predict(X_test)
train_acc_tree = accuracy_score(y_train_encoded, y_pred_train_tree)
test_acc_tree = accuracy_score(y_test_encoded, y_pred_test_tree)
print(f"Decision Tree Performance:")
print(f" Training Accuracy: {train_acc_tree:.4f}")
print(f" Test Accuracy: {test_acc_tree:.4f}")
print(f" Overfitting: {(train_acc_tree-test_acc_tree):.4f}")
# Feature Importance anzeigen
importances_tree = pd.DataFrame({
'Feature': feature_cols_encoded,
'Importance': tree_single.feature_importances_
}).sort_values('Importance', ascending=False)
print(f"\nFeature Importance:")
for _, row in importances_tree.iterrows():
print(f" {row['Feature']}: {row['Importance']:.4f}")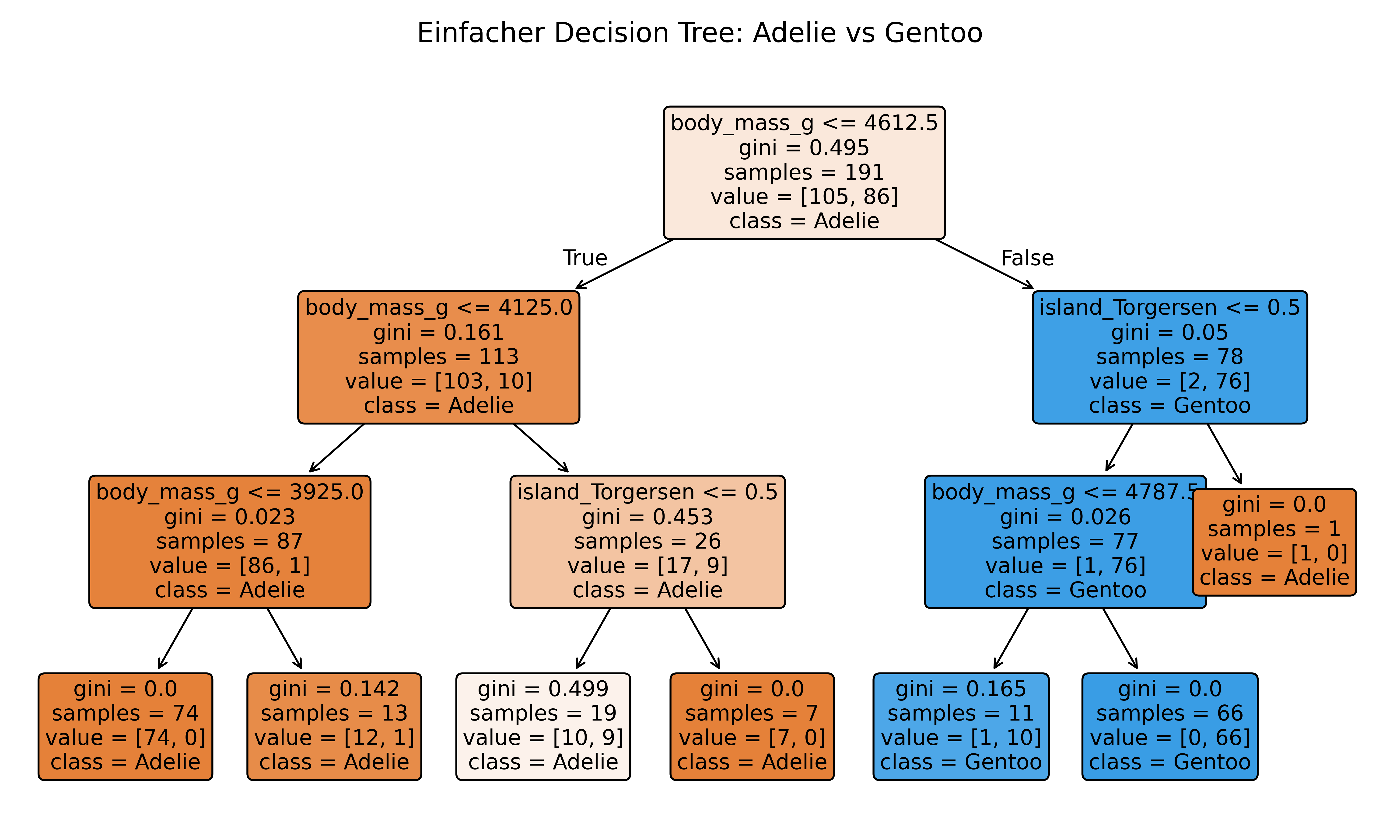
Decision Tree Performance:
Training Accuracy: 0.9424
Test Accuracy: 0.8313
Overfitting: 0.1111
Feature Importance:
body_mass_g: 0.9482
island_Torgersen: 0.0518
island_Dream: 0.0000Wie erwartet ist body_mass_g das wichtigste Feature. Die Trainings Accuracy beträgt ca. 94% (180/191), weil wie in der Visualisierung zu sehen in den Adelie-Blattknoten (=orange) insgesamt 10 Gentoo und in den Gentoo-Blattknoten (=blau) ein Adelie Pinguin gelandet ist. Die Accuracy für den Testdatensatz liegt bei 83%.
Random Forest
Random Forest kombiniert zwei wichtige Ideen, um aus identischen Trainingsdaten verschiedene Bäume zu erzeugen. Aber bevor wir die Theorie erklären, schauen wir uns auch hier erst ein konkretes Beispiel an.
Ein didaktisches Beispiel: Random Forest mit nur 3 Bäumen
Normalerweise verwendet man 50, 100 oder mehr Bäume in einem Random Forest. Für das Verständnis der Grundprinzipien beginnen wir jedoch mit nur 3 Bäumen, damit wir jeden einzelnen Baum komplett analysieren und das Voting-Verhalten genau verstehen können. Die Funktion, die wir benötigen heißt RandomForestClassifier() und das Argument n_estimators= lässt uns die Anzahl der Bäume wählen. Das Argument max_depth=3 gibt es hier genau wie vorher schon bei DecisionTreeClassifier() und es gilt auch eben genau so für jeden der vielen Bäume.
# Random Forest mit nur 3 Bäumen für didaktische Zwecke
rf_small = RandomForestClassifier(
n_estimators=3, # Nur 3 Bäume für vollständige Nachvollziehbarkeit
max_depth=3, # Gleiche Tiefe wie bei anderen Modellen
random_state=42, # Konsistent mit anderen Modellen für Reproduzierbarkeit
)
rf_small.fit(X_train, y_train_encoded);So erhalten wir tatsächlich drei verschiedene Bäume, die wir wie sonst auch visualisieren können. Ebenso können wir für jeden die Trainings- und Test-Accuracy usw. ausgeben lassen.
Code zeigen/verstecken
# Analyse der drei einzelnen Bäume
# print("Detailanalyse der 3 Bäume:\n")
tree_accuracies = []
tree_features = []
for i, tree in enumerate(rf_small.estimators_):
# Numpy arrays verwenden für einzelne Bäume (verhindert sklearn warnings)
train_acc = tree.score(X_train_np, y_train_encoded)
test_acc = tree.score(X_test_np, y_test_encoded)
# Ersten Split analysieren
root_feature_idx = tree.tree_.feature[0]
root_threshold = tree.tree_.threshold[0]
root_feature = feature_cols_encoded[root_feature_idx]
tree_accuracies.append(test_acc)
tree_features.append(root_feature)
#print(f"Random Forest Ensemble (3 Bäume): {rf_small.score(X_test, y_test_encoded):.4f} Test Accuracy")
#print(f"Vergleich mit Decision Tree: {tree_single.score(X_test, y_test_encoded):.4f} Test Accuracy")
#print(f"Verbesserung durch Ensemble: {(rf_small.score(X_test, y_test_encoded) - tree_single.score(X_test, y_test_encoded)):+.4f}")
# Alle drei Bäume in einem 2x2 Grid visualisieren
fig, axes = plt.subplots(2, 2, figsize=(11, 9), layout='tight')
# Dynamische tree_info basierend auf tatsächlichen Ergebnissen
tree_info = []
for i, (accuracy, feature) in enumerate(zip(tree_accuracies, tree_features)):
label = f"Baum {i+1}"
tree_info.append((label, feature, accuracy))
# Position im 2x2 Grid: (0,0), (0,1), (1,0)
positions = [(0, 0), (0, 1), (1, 0)]
for i, (tree, (title, first_feature, accuracy)) in enumerate(zip(rf_small.estimators_, tree_info)):
row, col = positions[i]
ax = axes[row, col]
plot_tree(tree,
feature_names=feature_cols_encoded,
class_names=['Adelie', 'Gentoo'],
filled=True,
rounded=True,
fontsize=8,
ax=ax);
full_title = f"{title}\n(Accuracy: {accuracy:.1%}, Start: {first_feature})";
ax.set_title(full_title, fontsize=12, pad=10);
# Das vierte Feld ausblenden
axes[1, 1].set_visible(False);
plt.show()
# Accuracies für jeden einzelnen Baum berechnen
for i, tree in enumerate(rf_small.estimators_):
# Für jeden Baum individuelle Accuracy berechnen
train_acc = tree.score(X_train_np, y_train_encoded)
test_acc = tree.score(X_test_np, y_test_encoded)
print(f"Baum {i+1}:")
print(f" Training Accuracy: {train_acc:.4f}")
print(f" Test Accuracy: {test_acc:.4f}")
print(f" Overfitting: {(train_acc-test_acc):.4f}")
print()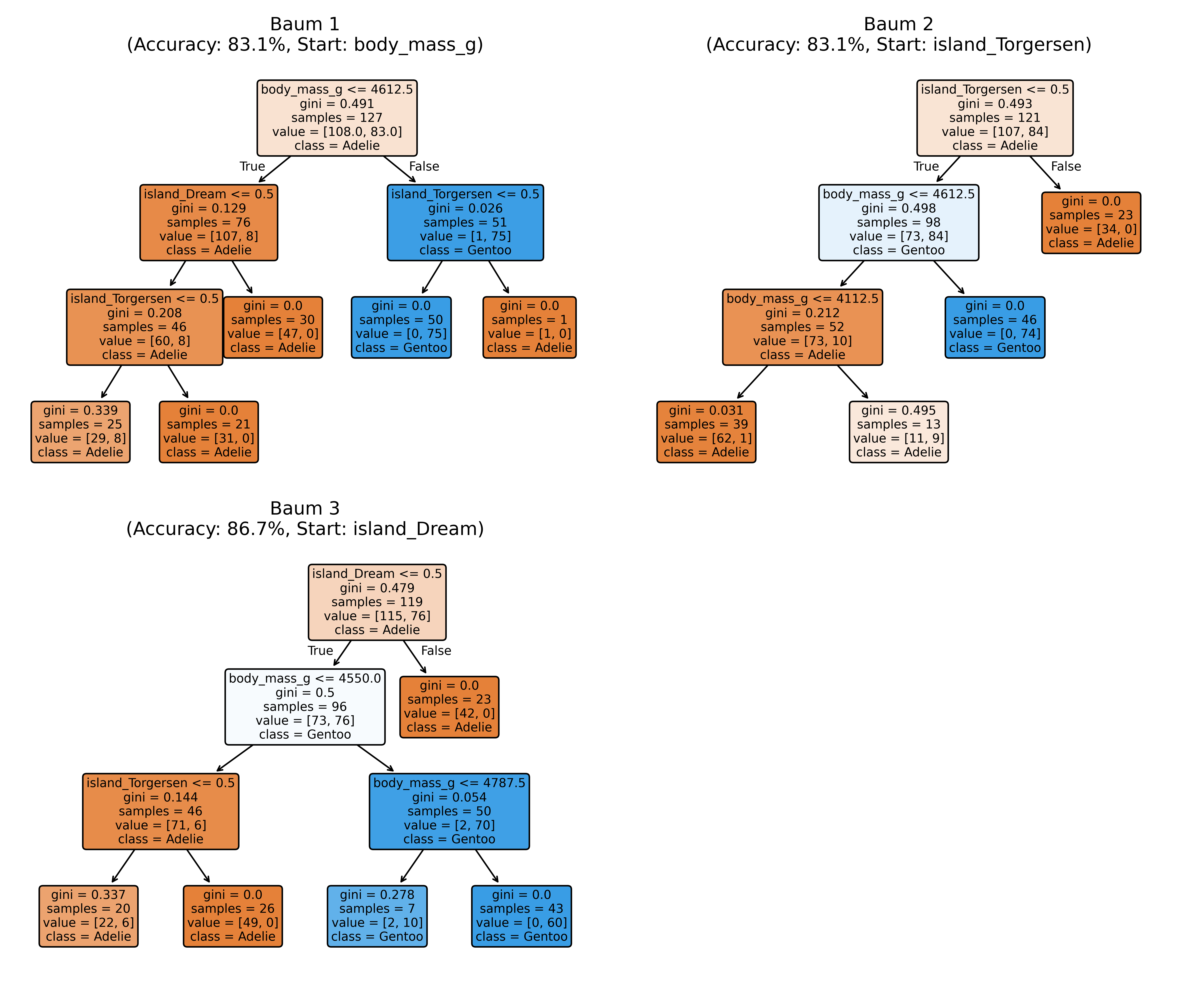
Baum 1:
Training Accuracy: 0.9424
Test Accuracy: 0.8313
Overfitting: 0.1111
Baum 2:
Training Accuracy: 0.9424
Test Accuracy: 0.8313
Overfitting: 0.1111
Baum 3:
Training Accuracy: 0.9372
Test Accuracy: 0.8675
Overfitting: 0.0697Bis hier hin ist also alles noch mehr oder weniger wie gewohnt. Und bzgl. der Test Accuracy erlangen die ersten zwei Bäume ja etwa dieselbe wie unser Einzelbaum von vorhin (83,1%), wobei der dritte Baum hier aber sogar eine leicht höhere (86,7%) hat. Es gilt nun aber zwei wichtige Dinge zu verstehen:
- Wie kann es überhaupt sein, dass verschiedene Bäume angepasst werden, wenn wir doch immer die gleichen Trainingsdaten zur Verfügung stellen?
- Wie bringen wir die verschiedenen Klassifizierungen pro Baum auf einen gemeinsamen Nenner?
Das wollen wir nun klären.
Wie entstehen verschiedene Bäume?
Versteht man einen Decision Tree, so weiß man: Wenn wir denselben Decision Tree Algorithmus mehrfach auf dieselben Daten anwenden, erhalten wir jedes Mal exakt denselben Baum. Das ist also keine Lösung. Stattdessen müssen wir ein wenig Zufall mit ins Spiel bringen.
Random Forest löst dieses Problem elegant durch zwei verschiedene Arten von Zufälligkeit:
Zufälligkeit 1: Bootstrap Sampling
Die erste Zufallskomponente liegt pro Baum in den Trainingsdaten selbst:
Jeder Baum wird eben nicht auf dem kompletten Trainingsdatensatz trainiert. Stattdessen wird für jeden Baum ein separater Datensatz mittels Bootstrapping erzeugt. Das bedeutet, dass so oft rein zufällig einzelne Zeilen des Trainingsdatensatz gezogen werden, bis ein Datensatz entstanden ist, der genau so viele Zeilen wie der ursprüngliche Trainingsdatensatz hat1. Der Trick ist, dass das zufällige Ziehen mit Zurücklegen ist, sodass einige Zeilen mehrfach und andere gar nicht gezogen werden. Tatsächlich ergibt sich dann mathematisch, dass immer etwa 37% aller ursprünglichen Datenzeilen außen vor bleiben (das wird nachher nochmal wichtig).
Der Begriff “Bootstrap” kommt aus dem Englischen und bezieht sich auf die Redewendung “sich an den eigenen Stiefelschlaufen [Bootstraps] aus dem Sumpf ziehen”. Das klingt paradox, aber es bedeutet im Grunde, dass man aus den vorhandenen Daten immer wieder neue Stichproben zieht und so versucht, möglichst viel Information aus diesen Daten herauszuholen.
Einigen ist vielleicht aufgefallen, dass in den jeweilige Root Nodes der drei Bäume unterschiedliche Anzahlen bei samples= steht, nämlich 127, 121 und 119. Das ist verwirrend, liegt aber nicht daran, dass tatsächlich eine unterschiedliche Anzahl Beobachtungen zum Trainieren genutzt wurde. Stattdessen zeigt sklearn hier die Anzahl der einzigartigen Beobachtungen im jeweiligen Bootstrap-Sample an, nicht die Gesamtanzahl der gezogenen Samples. Konkret bedeutet das: Obwohl für jeden Baum 191 Samples mit Zurücklegen gezogen wurden (genau so viele wie im Trainings-Datensatz), enthält das Bootstrap-Sample für Baum 1 nur 127 verschiedene, einzigartige Zeilen aus dem ursprünglichen Datensatz - die restlichen 64 Samples sind Duplikate von bereits gezogenen Zeilen (= entspricht den erwähnten 37%). Sklearn implementiert dies intern mit Sample-Gewichten anstatt die Zeilen physisch zu duplizieren, was speichereffizienter ist.
Für besonders interessierte ist hier ein weiterführendes, reproduzierbares Beispiel.
Zufälligkeit 2: Random Feature Selection
Die zweite Zufallskomponente greift sogar bei jedem einzelnen Split:
Bei jeder einzelnen Entscheidung eines jeden Baums werden dem Algorithmus zufällig nur einige Features angeboten. Es wird also zufällig nur eine Teilmenge der Features betrachtet. In scikit-learn ist die Standard-Anzahl: √(Anzahl aller Features).
Bei unseren 3 Features wird also pro Split nur √3 ≈ 1 Feature zufällig ausgewählt. Das ist nicht besonders optimal, wird aber für den Moment akzeptiert.
Das Abstimmen der Bäume
Da nun klar ist warum wir verschiedene Bäume erhalten, gilt es noch zu klären wie wir die unterschiedlichen Ergebnisse pro Baum zu einem gesamtheitlichen Ergebnis des Waldes machen können.
Tatsächlich befragt man sozusagen zu jedem einzelnen Datenpunkt wie jeder einzelne Baum diesen klassifizieren würde. Für uns heißt das, dass wir zu jedem der Pingiuine prüfen zu welcher Art sie laut welchem Baum gehören. Das wiederum bedeuet ja auch nur, dass wir für genau die Feature-Werte des Pinguins den einzelnen Baum von oben nach unten ablaufen, bis wir in einem Blattknoten gelandet sind.
Schauen wir uns das konkret für die ersten 5 Testpinguine an:
Code zeigen/verstecken
# Voting-Demonstration für erste 5 Testpinguine
print("Demokratische Abstimmung für erste 5 Testpinguine:\n")
for i in range(5):
# Einzelne Vorhersagen der drei Bäume (numpy arrays verwenden)
X_single = X_test_np[i:i+1] # Slice für 2D array
individual_preds = []
individual_probs = []
for tree in rf_small.estimators_:
pred = int(tree.predict(X_single)[0])
probs = tree.predict_proba(X_single)[0]
individual_preds.append(pred)
individual_probs.append(probs)
# Ensemble-Entscheidung (RF kann DataFrames verwenden)
ensemble_pred = int(rf_small.predict(X_test.iloc[[i]])[0])
ensemble_prob = rf_small.predict_proba(X_test.iloc[[i]])[0]
# Labels für Ausgabe
individual_labels = le_species.inverse_transform(individual_preds)
ensemble_label = le_species.inverse_transform([ensemble_pred])[0]
actual_label = y_test.iloc[i]
# Stimmenverteilung
adelie_votes = sum(1 for pred in individual_preds if pred == 0)
gentoo_votes = sum(1 for pred in individual_preds if pred == 1)
print(f"Pinguin {i+1:2d}:")
print(f" Baum 1: {individual_labels[0]:8s} (Conf: {max(individual_probs[0]):.3f})")
print(f" Baum 2: {individual_labels[1]:8s} (Conf: {max(individual_probs[1]):.3f})")
print(f" Baum 3: {individual_labels[2]:8s} (Conf: {max(individual_probs[2]):.3f})")
print(f" Abstimmung: {adelie_votes} x Adelie, {gentoo_votes} x Gentoo")
print(f" Ensemble: {ensemble_label:8s} (Conf: {max(ensemble_prob):.3f})")
print(f" Tatsächlich: {actual_label:8s} {'✓' if ensemble_label == actual_label else '✗'}")
print()
print()
print("...Pinguine 6 - 83...")Demokratische Abstimmung für erste 5 Testpinguine:
Pinguin 1:
Baum 1: Adelie (Conf: 0.784)
Baum 2: Adelie (Conf: 0.984)
Baum 3: Adelie (Conf: 0.786)
Abstimmung: 3 x Adelie, 0 x Gentoo
Ensemble: Adelie (Conf: 0.851)
Tatsächlich: Adelie ✓
Pinguin 2:
Baum 1: Adelie (Conf: 0.784)
Baum 2: Adelie (Conf: 0.550)
Baum 3: Gentoo (Conf: 0.833)
Abstimmung: 2 x Adelie, 1 x Gentoo
Ensemble: Adelie (Conf: 0.500)
Tatsächlich: Gentoo ✗
Pinguin 3:
Baum 1: Adelie (Conf: 0.784)
Baum 2: Adelie (Conf: 0.984)
Baum 3: Adelie (Conf: 0.786)
Abstimmung: 3 x Adelie, 0 x Gentoo
Ensemble: Adelie (Conf: 0.851)
Tatsächlich: Adelie ✓
Pinguin 4:
Baum 1: Gentoo (Conf: 1.000)
Baum 2: Gentoo (Conf: 1.000)
Baum 3: Gentoo (Conf: 0.833)
Abstimmung: 0 x Adelie, 3 x Gentoo
Ensemble: Gentoo (Conf: 0.944)
Tatsächlich: Adelie ✗
Pinguin 5:
Baum 1: Adelie (Conf: 0.784)
Baum 2: Adelie (Conf: 0.550)
Baum 3: Adelie (Conf: 0.786)
Abstimmung: 3 x Adelie, 0 x Gentoo
Ensemble: Adelie (Conf: 0.706)
Tatsächlich: Gentoo ✗
...Pinguine 6 - 83...So erhalten wir also eine Abstimmung. Interessanterweise wird diese Abstimmung in scikit-learn prinzipiell auf zwei verschiedene Arten ausgewertet und ausgegeben:
-
Entscheidung (
predict) - Hard Voting- Bei der eigentlichen Ja/Nein-Entscheidung zu welcher der beiden Klassen ein Pinguin nun laut Random Forest gehört, wird durch einfache Mehrheitswahl entschieden: jeder Baum gibt eine Stimme ab. Dies ist ein Hard Voting, weil eine Stimme immer gleich viel zählt - unabhängig davon wie sicher sich ein einzelner Baum ist2.
-
Wahrscheinlichkeit (
predict_proba) - Soft Voting- Bei der Wahrscheinlichkeit, die zur Ja/Nein-Entscheidung gehört, wird stattdessen der Mittelwert aller Wahrscheinlichkeiten der Einzelbäume gebildet. Das ist ein Soft Voting, da hier die Sicherheit jeder einzelnen Stimme ins Ergebnis eingeht3.
Die hier gesehene Vorgehensweise erst mittels Bootstrap mehrere Stichproben-Datensätze zu erzeugen und dann deren Ergebnisse zu aggregieren nennt man kurz auch Bagging. Tatsächlich könnte man ja auch nur genau das tun um diese Daten mittels Bagging auszuwerten. Ergänzt man dann aber eben noch die Random Feature Selection, so gilt erst das dann als Random Forest Ansatz.
Sowohl für Hard Voting als auch für Soft Voting lassen sich Argumente finden warum es geeignete Methoden zum Aggregieren der Einzelbaumergebnisse sind. Dadurch, dass hier in scikit-learn aber beide genutzt werden, kann es in seltenen Fällen vorkommen, dass eine Diskrepanz zwischen den Ergebnissen entsteht: Würden zwei Bäume mit einer Wahrscheinlichkeit von 0.51 für Klasse A stimmen, aber ein Baum mit einer Wahrscheinlichkeit von 0.98 für Klasse B (also 0.02 für Klasse A), so wäre das Hard Voting 2 zu 1 für Klasse A, aber die mittlere Wahrscheinlichkeit für Klasse A nur (0.51 + 0.51 + 0.02)/3 = 0.34.
Wie hat nun also unser Random Forest (mit nur 3 Bäumen!) abgeschnitten? Wir vergleichen:
Code zeigen/verstecken
print("Test Accuracy:")
print(f" Einzelner Decision Tree: {tree_single.score(X_test, y_test_encoded):.4f}")
individual_test_scores = [tree.score(X_test_np, y_test_encoded) for tree in rf_small.estimators_]
print(" Einzelne Bäume im Random Forest:")
for i, score in enumerate(individual_test_scores):
print(f" Baum {i+1}: {score:.4f}")
print(f" Random Forest Ensemble (3 Bäume): {rf_small.score(X_test, y_test_encoded):.4f}")Test Accuracy:
Einzelner Decision Tree: 0.8313
Einzelne Bäume im Random Forest:
Baum 1: 0.8313
Baum 2: 0.8313
Baum 3: 0.8675
Random Forest Ensemble (3 Bäume): 0.8313Antwort: Nicht so besonders - wir sehen noch keine Verbesserung. Das liegt aber vor allem daran, dass es bisher nur ein Wäldchen und wohl kaum ein Wald ist, wie wir gleich sehen werden.
Random Forest mit 100 Bäumen
Nachdem wir das Prinzip mit 3 Bäumen verstanden haben, verwenden wir nun eine üblichere Anzahl von 100 Bäumen für bessere Performance:
# Random Forest mit 100 Bäumen für produktiven Einsatz
rf = RandomForestClassifier(
n_estimators=100, # Jetzt 100 Bäume statt 3
max_depth=3, # Gleiche Tiefe wie bei anderen Modellen
oob_score=True, # Out-of-Bag Score berechnen (Info folgt gleich)
random_state=42 # Konsistent für Reproduzierbarkeit
);
rf.fit(X_train, y_train_encoded);
# Performance bewerten
y_pred_train_rf = rf.predict(X_train)
y_pred_test_rf = rf.predict(X_test)
train_acc_rf = accuracy_score(y_train_encoded, y_pred_train_rf)
test_acc_rf = accuracy_score(y_test_encoded, y_pred_test_rf)
print(f"Random Forest (100 Bäume) Performance:")
print(f" Training Accuracy: {train_acc_rf:.4f}")
print(f" Test Accuracy: {test_acc_rf:.4f}")
print(f" Overfitting: {(train_acc_rf-test_acc_rf):.4f}")
print(f" Out-of-Bag Score: {rf.oob_score_:.4f} (Info folgt gleich)")
print()
print(f"Vergleich mit Decision Tree:")
print(f" Decision Tree Test Accuracy: {test_acc_tree:.4f}")
print(f" Random Forest Test Accuracy: {test_acc_rf:.4f}")Random Forest (100 Bäume) Performance:
Training Accuracy: 0.9634
Test Accuracy: 0.9398
Overfitting: 0.0236
Out-of-Bag Score: 0.9529 (Info folgt gleich)
Vergleich mit Decision Tree:
Decision Tree Test Accuracy: 0.8313
Random Forest Test Accuracy: 0.9398Verbesserung: Der 100-Baum Random Forest erreicht 93.98% Accuracy verglichen mit 83.13% des einzelnen Decision Tree - eine Verbesserung von +10.84 Prozentpunkten! Dies demonstriert also hier die “Weisheit der Massen”.
Leider gibt es keine so schöne/intuitive Visualisierung für Random Forests. 100 Bäume nebeneinander abzubilden ist natürlich keine Lösung. Wir können aber z.B. die Feature Importance der bisherigen 3 Ansätze vergleichen:
Code zeigen/verstecken
# Feature Importance vergleichen: Decision Tree vs beide Random Forest Varianten
importances_comparison = pd.DataFrame({
'Feature': feature_cols_encoded,
'Decision_Tree': tree_single.feature_importances_,
'Random_Forest_3': rf_small.feature_importances_,
'Random_Forest_100': rf.feature_importances_
}).sort_values('Random_Forest_100', ascending=False)
# print("Feature Importance Vergleich:")
# print(importances_comparison.round(4))
# Feature Importance visualisieren
fig, ax = plt.subplots(figsize=(8, 5), layout='tight')
x_pos = np.arange(len(feature_cols_encoded))
width = 0.25
ax.bar(x_pos - width, importances_comparison['Decision_Tree'], width,
label='Decision Tree', alpha=0.8, color='skyblue');
ax.bar(x_pos, importances_comparison['Random_Forest_3'], width,
label='Random Forest (3 Bäume)', alpha=0.8, color='lightgreen');
ax.bar(x_pos + width, importances_comparison['Random_Forest_100'], width,
label='Random Forest (100 Bäume)', alpha=0.8, color='darkgreen');
ax.set_xlabel('Features');
ax.set_ylabel('Importance');
ax.set_title('Feature Importance: Decision Tree vs Random Forest Varianten');
ax.set_xticks(x_pos);
ax.set_xticklabels(importances_comparison['Feature'], rotation=45, ha='right');
ax.legend();
ax.grid(True, alpha=0.3);
plt.show()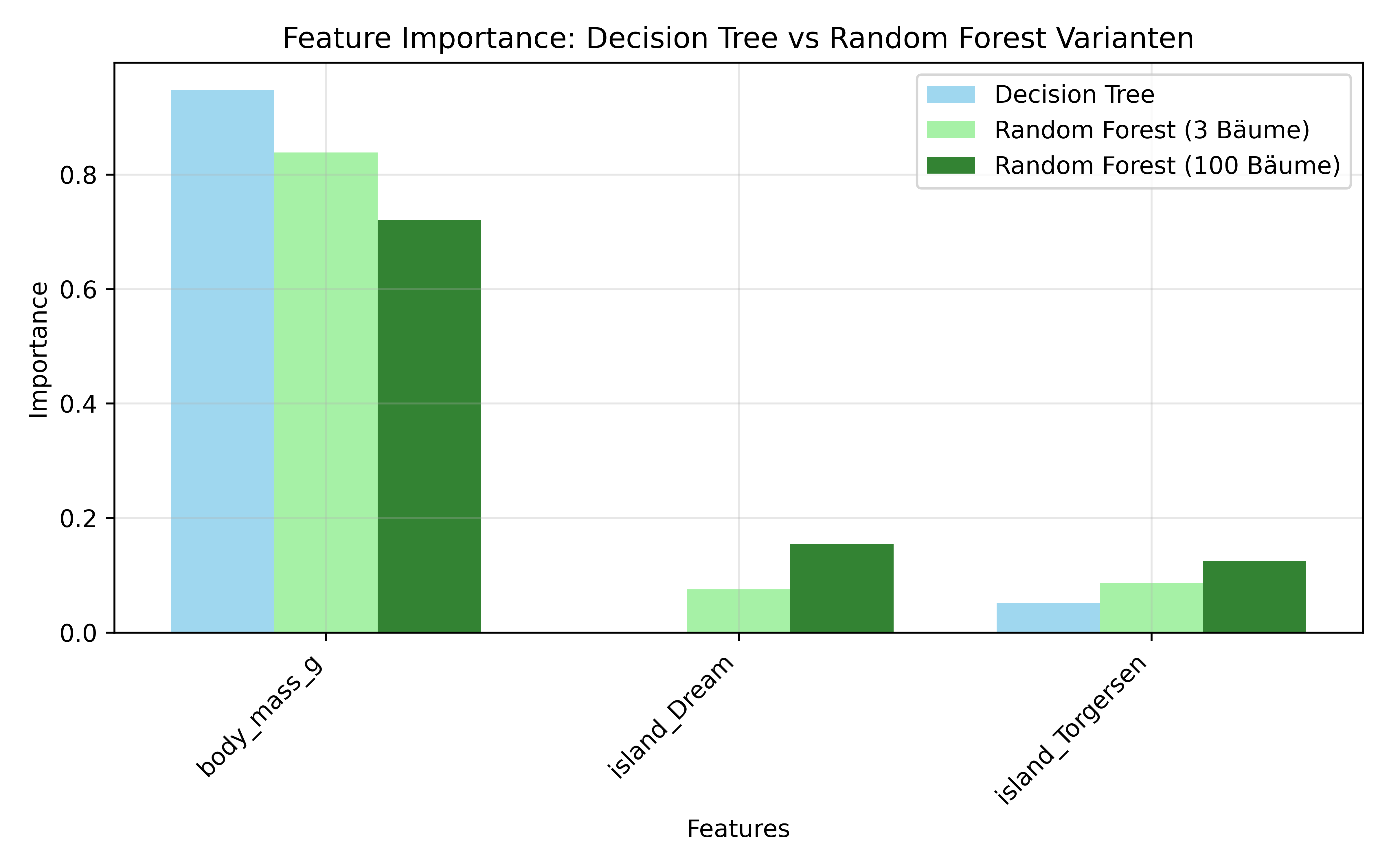
Random Forest nutzt die Features etwas ausgewogener als der einzelne Decision Tree - der Decision Tree fokussiert fast nur auf body_mass_g (94.8%), während Random Forest auch den Insel-Features mehr Gewicht gibt (15.5% + 12.4%).
Warum funktioniert das so gut?
Random Forest kombiniert gezielte Schwächung einzelner Bäume mit kollektiver Stärke des Ensembles – und das auf beeindruckend effektive Weise. Zwei zentrale Ideen machen das möglich:
Zufall schafft Vielfalt: Durch Bootstrapping (Zufall bei den Daten) und zufällige Feature-Auswahl (Zufall bei den Splits) entstehen viele unterschiedliche Bäume – auch wenn sie alle mit denselben Einstellungen auf denselben Trainings-Datensatz angewendet werden.
Vielfalt reduziert Überanpassung: Jeder einzelne Baum mag durch diese Einschränkungen etwas weniger leistungsfähig sein. Aber genau das ist erwünscht – denn wenn alle Bäume die gleichen Muster lernen, bringt das Ensemble keinen Vorteil. Die Stärke entsteht gerade durch die Unterschiede: Während der eine Baum ein bestimmtes Muster falsch interpretiert, erkennt es ein anderer richtig – und der Wald als Ganzes trifft dank Mehrheitsentscheid meist die richtige Wahl.
Ein Random Forest lebt also davon, dass viele unterschiedlich gute Bäume unterschiedliche Perspektiven einbringen. Das reduziert die Wahrscheinlichkeit, dass sich alle im selben Irrtum einig sind. In der Summe entsteht so ein robustes und stabiles Modell, das weniger anfällig für zufällige Schwankungen im Datensatz ist – und genau deshalb oft deutlich besser generalisiert als ein einzelner perfektionistisch überanpassender Baum.
Out-of-Bag Score: Ein Bonus des Random Forest
Wir haben weiter oben bereits gesagt, dass beim Random Forest für jeden einzelnen Baum ein eigenes Bootstrap-Sample aus den Trainingsdaten gezogen wird. Dadurch bleiben im Schnitt wie gesagt etwa 37% der Daten pro Baum unberücksichtigt. Diese Beobachtungen nennt man Out-of-Bag (OOB) – also „außerhalb des Beutels” und passend zum Term Bagging, d.h. nicht in den Trainingsdaten dieses Baumes enthalten.
Diese ungenutzten 37% Beobachtungen pro Baum muss man nicht ungenutzt lassen!
Die clevere Idee: Diese OOB-Beobachtungen können genutzt werden, um die Modellgüte abzuschätzen – und zwar ohne separaten Testdatensatz. Im Endeffekt ist es ja auch einfach nur sowas ein separater Testdatensatz, allerdings ist er zufällig als Nebenprodukt des Bootstrap-Sampling entstanden und das jeweils pro Baum. Wir lassen den einzelnen, auf den Bootstrap-Daten trainierten Baum die OOB-Beobachtungen klassifizieren und gleichen es mit ihrer tatsächlichen Klasse ab. Der OOB-Score ist dann der Anteil korrekt vorhergesagter Beobachtungen unter allen OOB-Vorhersagen - also auch wie Accuracy.
print(f"OOB Score des Random Forests: {rf.oob_score_:.4f}")OOB Score des Random Forests: 0.9529Der große Vorteil ist natürlich, dass wir keine Daten „weglegen” für ein Testset, sondern eine Abschätzung der Generalisierungsfähigkeit quasi nebenbei erhalten. Zudem basiert der Score auf echten Test-Situationen: Jeder Baum trifft Vorhersagen für Beobachtungen, die er nie gesehen hat.
Allerdings ist der OOB-Score nicht identisch mit einer echten k-fachen Kreuzvalidierung. Der Unterschied liegt darin, dass die Zuordnung zu Training und Test bei OOB zufällig und ungleichmäßig geschieht. Manche Beobachtungen sind in vielen Bäumen OOB, andere in nur wenigen. Dadurch kann der OOB-Score in manchen Fällen leicht optimistisch verzerrt sein – insbesondere bei kleineren Datensätzen oder wenn viele Hyperparameter getuned werden.
In der Praxis hat sich aber gezeigt: Für erste Einschätzungen ist der OOB-Score meist sehr zuverlässig – insbesondere bei großen Random Forests mit vielen Bäumen. Er ist schnell, dateneffizient und direkt integriert. Spätestens aber weil andere Klassifikationsalgorithmen keinen OOB-Score liefern, braucht es für den fairen Modellvergleich trotzdem wieder ein gemeinsames Maß – etwa einen klassischen Testdatensatz mit Cross-Validation.
Gradient Boosting (Ausblick)
Die zweite große Klasse von Ensemble-Methoden nach Random Forest heißt Gradient Boosting – und sie wäre eigentlich der nächste logische Schritt in unserer Reise durch fortgeschrittene Klassifikationsverfahren. Allerdings ist das Konzept nochmal komplexer, und seine volle Erklärung würde den Rahmen unseres Kurses sprengen. Wer sich für diese Technik interessiert, sollte sie sich bei Bedarf selbst anlesen. Dennoch wollen wir uns kurz ein grobes Gefühl dafür verschaffen, wie Gradient Boosting grundsätzlich funktioniert und wie es sich von Random Forest unterscheidet.
Während Random Forest viele Bäume parallel trainiert und dabei versucht, Überanpassung durch Variation der Modelle zu vermeiden, verfolgt Gradient Boosting eine ganz andere Strategie: Fehlerkorrektur in Serie. Es beginnt mit einem einfachen, schwachen Modell – z.B. einem sehr kleinen Decision Tree – und versucht dann, die Fehler dieses Modells durch einen zweiten kleinen Baum zu korrigieren. Danach wird der dritte Baum trainiert, um die noch verbleibenden Fehler zu korrigieren, und so weiter. Jeder Baum lernt also auf Basis der Fehler der vorherigen Bäume, was diesen Ansatz zu einem sequenziellen Verfahren macht.
Da jeder neue Baum nur noch kleine Verbesserungen liefern soll, ist es besonders wichtig, dass man nicht zu große Schritte macht. Dieser Schrittweiten-Regler nennt sich learning_rate – und bestimmt, wie stark ein Baum seine Korrektur beisteuert. Dadurch entsteht ein fein abgestimmtes Zusammenspiel vieler kleiner Modelle, was oft zu sehr guter Performance führt, aber auch eine erhöhte Gefahr von Overfitting mit sich bringt.
Gradient Boosting ist also ebenfalls ein Ensemble-Verfahren, aber im Gegensatz zum Random Forest gibt es kein Bootstrapping, kein Feature Sampling und auch kein Voting. Stattdessen wird eine Art “Fehler-Lernkette” gebildet, die am Ende ein starkes Modell ergibt – wenn man es richtig einstellt. Das macht Gradient Boosting potenziell leistungsfähiger, aber eben auch anfälliger für Fehlkonfiguration und schwerer zu interpretieren.
In vielen realen Projekten begegnet einem Gradient Boosting in Form von leistungsstarken spezialisierten Bibliotheken wie XGBoost, LightGBM oder CatBoost. Im Vergleich zu scikit-learn implementieren diese das Grundprinzip effizienter, erlauben umfangreicheres Tuning, und sind oft die erste Wahl bei Kaggle-Wettbewerben. Für uns genügt aber das Grundverständnis – wer tiefer einsteigen möchte, kann sich diese Tools später selbst anschauen.
Im Folgenden führen wir Gradient Boosting einmal exemplarisch durch – mit denselben Einstellungen wie beim Random Forest (100 Bäume, maximale Tiefe 3) – und vergleichen die Test-Performance:
# Gradient Boosting Klassifikator
gb = GradientBoostingClassifier(
n_estimators=100, # Anzahl Bäume (sequenziell trainiert)
max_depth=3, # Tiefe der Einzelbäume (weak learners)
learning_rate=0.1, # Lernrate: Schrittweite zur Fehlerkorrektur
random_state=42
)
gb.fit(X_train, y_train_encoded)
# Vorhersagen und Performance
y_pred_train_gb = gb.predict(X_train)
y_pred_test_gb = gb.predict(X_test)
train_acc_gb = accuracy_score(y_train_encoded, y_pred_train_gb)
test_acc_gb = accuracy_score(y_test_encoded, y_pred_test_gb)
print(f"Gradient Boosting Performance:")
print(f" Training Accuracy: {train_acc_gb:.4f}")
print(f" Test Accuracy: {test_acc_gb:.4f}")
print(f" Overfitting: {(train_acc_gb-test_acc_gb):.4f}")
print()GradientBoostingClassifier(random_state=42)
Gradient Boosting Performance:
Training Accuracy: 0.9843
Test Accuracy: 0.9518
Overfitting: 0.0325Gradient Boosting ist also ebenfalls ein Ensemble – aber ein ganz anderes als der Random Forest. Und auch wenn wir es hier nicht im Detail sezieren, sieht man: Es kann sich lohnen. Mit überschaubarem Code erreicht das Modell noch einmal eine höhere Testgenauigkeit – aber das Feintuning und das Verständnis der zugrundeliegenden Optimierung bleiben Themen für ein späteres Kapitel oder ein weiterführendes Projekt.
Methodenvergleich
Wir haben jetzt vier verschiedene Ansätze kennengelernt: einen einzelnen Decision Tree, einen Random Forest mit 3 Bäumen, einen Random Forest mit 100 Bäumen und Gradient Boosting. Zeit für einen systematischen Vergleich!
Übersicht: Test Accuracy und Feature Importance
Zunächst fassen wir die bereits berechneten Ergebnisse aus unserem einmaligen Train-Test Split zusammen:
Code zeigen/verstecken
# Test Accuracy aller Methoden sammeln
test_accuracies = {
'Decision Tree': test_acc_tree,
'Random Forest (3 Bäume)': rf_small.score(X_test, y_test_encoded),
'Random Forest (100 Bäume)': test_acc_rf,
'Gradient Boosting': test_acc_gb
}
# Ergebnisse anzeigen
print("Test Accuracy Vergleich (einmaliger Train-Test Split):")
for method, accuracy in test_accuracies.items():
print(f" {method}: {accuracy:.4f}")
print()
# Feature Importance aller Methoden vergleichen (alle Modelle sind bereits trainiert)
all_importances = pd.DataFrame({'Feature': feature_cols_encoded})
all_importances['Decision_Tree'] = tree_single.feature_importances_
all_importances['Random_Forest_3'] = rf_small.feature_importances_
all_importances['Random_Forest_100'] = rf.feature_importances_
all_importances['Gradient_Boosting'] = gb.feature_importances_
# Feature Importance visualisieren
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
x_pos = np.arange(len(feature_cols_encoded))
width = 0.2
ax.bar(x_pos - 1.5*width, all_importances['Decision_Tree'], width,
label='Decision Tree', alpha=0.8, color='skyblue');
ax.bar(x_pos - 0.5*width, all_importances['Random_Forest_3'], width,
label='Random Forest (3 Bäume)', alpha=0.8, color='lightgreen');
ax.bar(x_pos + 0.5*width, all_importances['Random_Forest_100'], width,
label='Random Forest (100 Bäume)', alpha=0.8, color='darkgreen');
ax.bar(x_pos + 1.5*width, all_importances['Gradient_Boosting'], width,
label='Gradient Boosting', alpha=0.8, color='orange');
ax.set_xlabel('Features');
ax.set_ylabel('Importance');
ax.set_title('Feature Importance: Alle Methoden im Vergleich');
ax.set_xticks(x_pos);
ax.set_xticklabels(all_importances['Feature'], rotation=45, ha='right');
ax.legend();
ax.grid(True, alpha=0.3);
plt.show()Test Accuracy Vergleich (einmaliger Train-Test Split):
Decision Tree: 0.8313
Random Forest (3 Bäume): 0.8313
Random Forest (100 Bäume): 0.9398
Gradient Boosting: 0.9518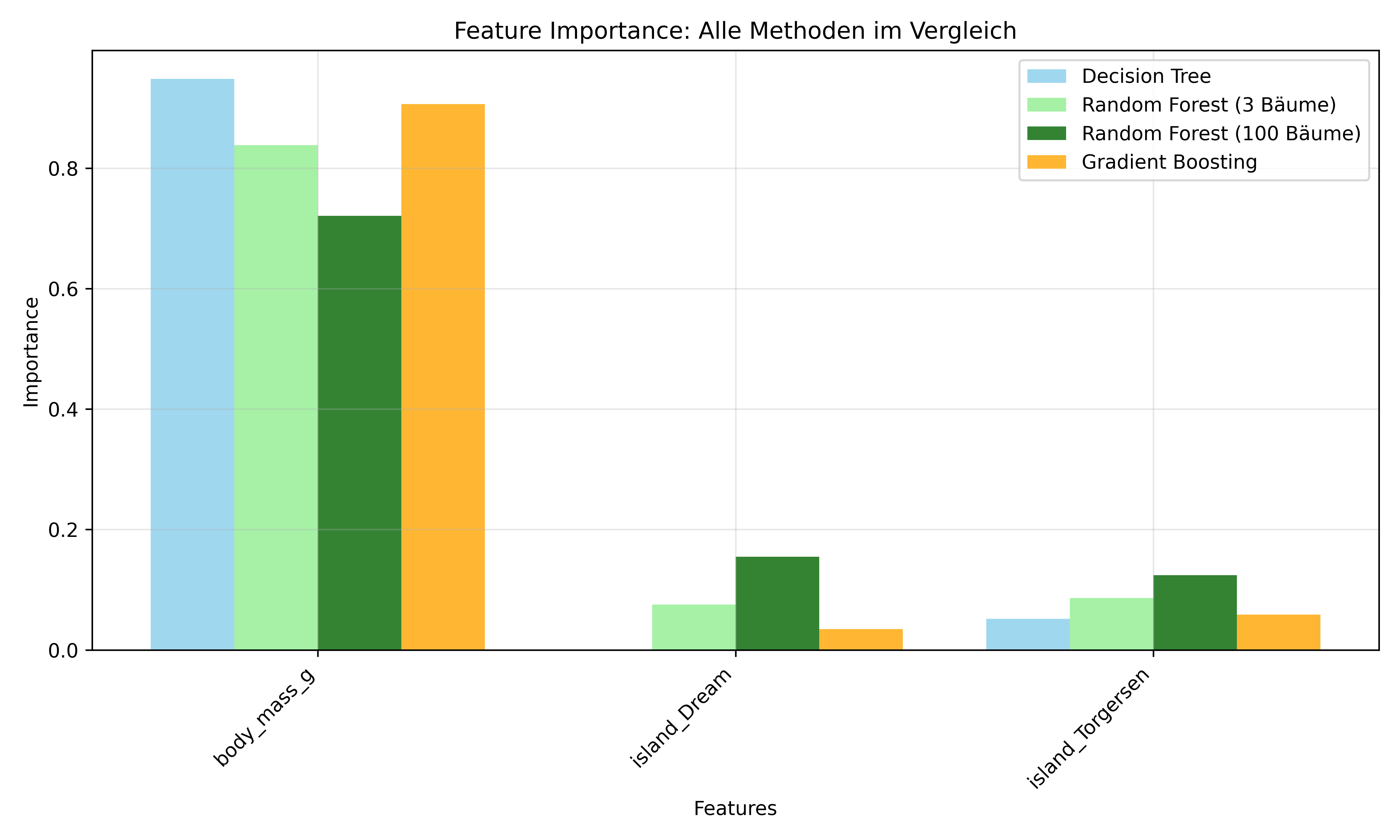
Wir können also festhalten, dass hier die Ensemble-Methoden durchaus besser klassifizieren konnten als der einzelne Decision Tree. Was wir jetzt allerdings die ganze Zeit nur betrachtet haben ist ein einzige Trainings-Test-Split. Um das ganze also noch auf fundiertere Füße zu stellen, sollten wir wie immer eine Kreuzvalidierung durchführen.
Robuste Bewertung mit Kreuzvalidierung
Für eine fundierte Methodenbewertung führen wir eine umfassende Kreuzvalidierung mit allen vier Ansätzen durch. Das folgende Code-Chunk ist vollständig isoliert und könnte eigenständig ausgeführt werden:
# Notwendige Module importieren
import pandas as pd
import numpy as np
from sklearn.model_selection import RepeatedStratifiedKFold, cross_validate
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.preprocessing import LabelEncoder
import matplotlib.pyplot as plt
np.random.seed(42)
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Daten für binäre Klassifikation vorbereiten (Adelie vs Gentoo)
penguins_binary = penguins[penguins['species'].isin(['Adelie', 'Gentoo'])].copy()
feature_cols = ['body_mass_g', 'island']
penguins_clean = penguins_binary[feature_cols + ['species']].dropna()
# One-Hot-Encoding für kategorische Variable
penguins_encoded = pd.get_dummies(penguins_clean, columns=['island'], drop_first=True)
feature_cols_encoded = [col for col in penguins_encoded.columns if col != 'species']
# Features und Target definieren
X = penguins_encoded[feature_cols_encoded]
y = penguins_encoded['species']
# Binäre Zielvariable erstellen (0 = Adelie, 1 = Gentoo)
y_binary = (y == 'Gentoo').astype(int)
# Alle vier Modelle definieren
models = {
'Decision Tree': DecisionTreeClassifier(max_depth=3, random_state=42),
'Random Forest (3 Bäume)': RandomForestClassifier(n_estimators=3, max_depth=3, random_state=42),
'Random Forest (100 Bäume)': RandomForestClassifier(n_estimators=100, max_depth=3, random_state=42),
'Gradient Boosting': GradientBoostingClassifier(n_estimators=100, max_depth=3, learning_rate=0.1, random_state=42)
}
# Repeated Stratified K-Fold für balancierte Test-Sets
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=10, random_state=42)
# Cross Validation für alle Modelle durchführen
cv_results = {}
feature_importance_results = {}
for name, model in models.items():
# Cross Validation mit mehreren Metriken
cv_result = cross_validate(
model, X, y_binary,
cv=cv,
scoring=['accuracy', 'precision', 'recall', 'f1', 'roc_auc'],
return_train_score=True
);
cv_results[name] = cv_result
# Feature Importance berechnen (Modell einmal auf allen Daten trainieren)
model.fit(X, y_binary);
feature_importance_results[name] = model.feature_importances_;
# Ergebnisse in übersichtlicher Tabelle organisieren
results_summary = []
metrics = ['accuracy', 'precision', 'recall', 'f1', 'roc_auc']
for metric in metrics:
metric_results = {'Metrik': metric.upper()}
for name in models.keys():
test_scores = cv_results[name][f'test_{metric}']
metric_results[name] = f"{test_scores.mean():.3f} (±{test_scores.std():.3f})"
results_summary.append(metric_results)
# Ergebnistabelle anzeigen
results_df = pd.DataFrame(results_summary)
print("Kreuzvalidierungs-Ergebnisse (50 Folds: 5×10 Wiederholungen):")
print(results_df.to_string(index=False))
print()
# Feature Importance Vergleich
feature_importance_df = pd.DataFrame(feature_importance_results, index=feature_cols_encoded)
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
x_pos = np.arange(len(feature_cols_encoded))
width = 0.2
colors_methods = ['skyblue', 'lightgreen', 'darkgreen', 'orange']
for i, (name, color) in enumerate(zip(models.keys(), colors_methods)):
ax.bar(x_pos + i*width - 1.5*width, feature_importance_df[name], width,
label=name, alpha=0.8, color=color);
ax.set_xlabel('Features');
ax.set_ylabel('Feature Importance');
ax.set_title('Feature Importance: Kreuzvalidierungs-Vergleich aller Methoden');
ax.set_xticks(x_pos);
ax.set_xticklabels(feature_cols_encoded);
ax.legend();
ax.grid(True, alpha=0.3);
plt.show()
# Beste Methode identifizieren
best_accuracy_scores = {}
for name in models.keys():
test_scores = cv_results[name]['test_accuracy']
best_accuracy_scores[name] = test_scores.mean()
best_method = max(best_accuracy_scores, key=best_accuracy_scores.get)
best_score = best_accuracy_scores[best_method]
print(f"Beste Methode: {best_method} mit {best_score:.3f} Accuracy")Kreuzvalidierungs-Ergebnisse (50 Folds: 5×10 Wiederholungen):
Metrik Decision Tree Random Forest (3 Bäume) Random Forest (100 Bäume) Gradient Boosting
ACCURACY 0.939 (±0.035) 0.946 (±0.034) 0.954 (±0.025) 0.961 (±0.024)
PRECISION 0.946 (±0.055) 0.954 (±0.038) 0.951 (±0.037) 0.951 (±0.036)
RECALL 0.921 (±0.068) 0.928 (±0.074) 0.950 (±0.049) 0.964 (±0.047)
F1 0.931 (±0.040) 0.938 (±0.041) 0.949 (±0.029) 0.956 (±0.027)
ROC_AUC 0.974 (±0.020) 0.984 (±0.015) 0.987 (±0.013) 0.986 (±0.012)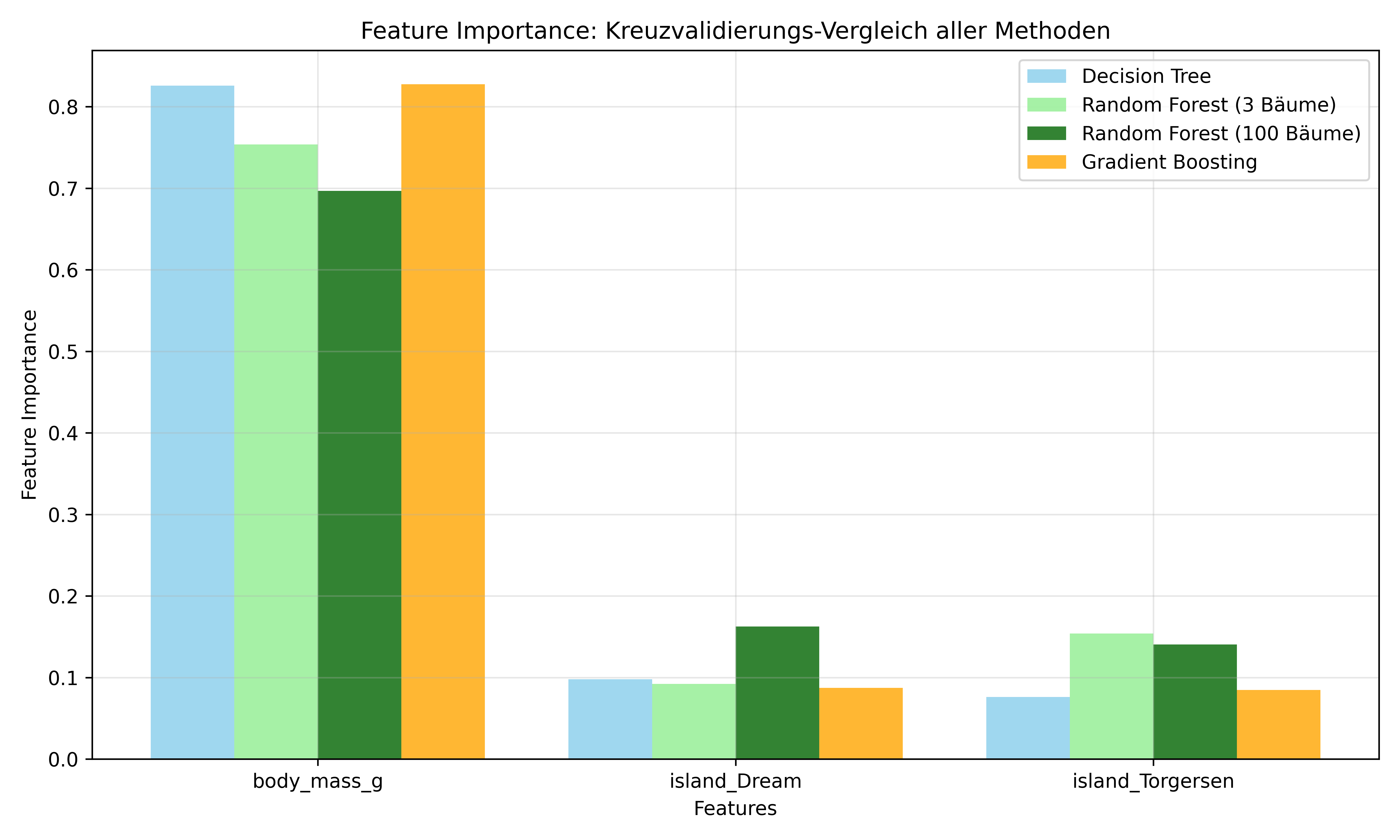
Beste Methode: Gradient Boosting mit 0.961 AccuracyDie Unterschiede zwischen den Methoden sind deutlich geringer als beim einmaligen Train-Test Split suggeriert. Während dort Random Forest (100 Bäume) und Gradient Boosting um 10+ Prozentpunkte besser abschnitten als der Decision Tree, zeigt die robustere Bewertung nur noch Unterschiede von etwa 2 Prozentpunkten (93.9% vs. 96.1%). Das ist an sich schon lehrreich - es zeigt, wie wichtig eine solide Validierungsmethodik ist, um Algorithmen fair zu bewerten. Dennoch bleibt die Rangfolge bestehen: Gradient Boosting führt knapp vor Random Forest (100 Bäume), gefolgt von Random Forest (3 Bäume) und dem einzelnen Decision Tree. Die Ensemble-Methoden zeigen also auch bei robuster Bewertung ihre Überlegenheit - wenn auch in moderaterem Ausmaß als zunächst vermutet.
Wann welche Methode verwenden?
Die Wahl zwischen den Ensemble-Methoden hängt von verschiedenen Faktoren ab:
Decision Trees bleiben wertvoll wenn:
- Maximale Interpretierbarkeit erforderlich ist
- Einfache, nachvollziehbare Regeln gebraucht werden
- Die Datenmenge klein ist
- Schnelle Vorhersagen wichtig sind
Random Forest ist ideal wenn:
- Robustheit und Stabilität wichtig sind
- Wenig Tuning-Aufwand gewünscht ist
- Out-of-Bag Evaluation nützlich ist
- Interpretierbarkeit durch Feature Importance ausreicht
- Parallelisierung möglich ist (Bäume unabhängig trainierbar)
Gradient Boosting eignet sich wenn:
- Maximale Vorhersagegenauigkeit angestrebt wird
- Zeit für Hyperparameter-Tuning vorhanden ist
- Learning Curves zur Optimierung genutzt werden können
- Overfitting durch Monitoring kontrolliert werden kann
- Sequenzielles Training akzeptabel ist
Übungen
Aufgabe 1: Random Forest Performance mit allen verfügbaren Features
In der Hauptanalyse dieses Kapitels haben wir bewusst nur wenige Features verwendet (body_mass_g und island), um die Unterschiede zwischen einzelnen Decision Trees und Random Forest deutlich zu demonstrieren. Jetzt soll untersucht werden, wie sich die Modelle verhalten, wenn alle verfügbaren numerischen und kategorialen Features zur Verfügung stehen.
Führe einen systematischen Vergleich von vier Modellen durch:
-
Decision Tree (mit
max_depth=3) -
Random Forest mit 3 Bäumen (mit
max_depth=3)
-
Random Forest mit 50 Bäumen (mit
max_depth=3) -
Random Forest mit 100 Bäumen (mit
max_depth=3)
Vorgehen:
- Verwende alle verfügbaren Features aus dem Palmer Penguins Datensatz (numerische und dummy-codierte kategorische)
- ABER: Schließe dabei
rowid(technischer Index) undflipper_length_mmaus - Führe eine Repeated Stratified K-Fold Cross Validation durch (
n_splits=5,n_repeats=10) - Berechne die Metriken:
accuracy,precision,recall,f1 - Erstelle eine Ergebnistabelle mit Durchschnitt und Standardabweichung für jede Metrik
- Visualisiere die Feature Importance aller vier Modelle in einem Balkendiagramm
- Identifiziere das beste Modell basierend auf der Test-Accuracy
Aufgabe 2: Visualisierung um Random Forest erweitern
Im Kapitel 055 “Klassifikationsgrenzen visualisieren” haben wir gelernt, wie man die Entscheidungsgrenzen von Klassifikationsalgorithmen für genau zwei numerische Features visualisiert. Am Ende wurde ein 2×2 Subplot erstellt, der logistische Regression und Decision Trees direkt vergleicht.
Erweitere diese Visualisierung um Random Forest als dritte Methode, sodass ein 3×2 Layout entsteht: Logistische Regression (oben), Decision Tree (mitte), Random Forest (unten).
Vorgaben:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
np.random.seed(42)
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
# Nur Gentoo und Adelie Pinguine auswählen (EXAKT wie in 055!)
penguins_binary = penguins[penguins['species'].isin(['Gentoo', 'Adelie'])].copy()
penguins_binary = penguins_binary.dropna(subset=['body_mass_g', 'flipper_length_mm'])
# Binäre Zielvariable erstellen (0 = Adelie, 1 = Gentoo)
penguins_binary['species_binary'] = (penguins_binary['species'] == 'Gentoo').astype(int)
# Features und Ziel definieren
X = penguins_binary[["body_mass_g", "flipper_length_mm"]].values
y = penguins_binary["species_binary"].values
# Train-Test Split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)Aufgabe:
-
Kopiere die
plot_classifier()Funktion aus Kapitel 055 (vollständig und unverändert) - Trainiere drei Modelle:
- Logistische Regression (
random_state=42) - Decision Tree (
max_depth=4,random_state=42) - Random Forest (
n_estimators=100,max_depth=4,random_state=42)
- Logistische Regression (
- Erstelle ein 3×2 Subplot-Layout mit
fig, axes = plt.subplots(3, 2, figsize=(14, 15), layout='tight', sharex=True, sharey=True) - Verwende für alle drei Modelle:
proba=True,xlabel="body_mass_g",ylabel="flipper_length_mm" - Setze den Gesamttitel:
"Logistische Regression (oben) vs. Decision Tree (mitte) vs. Random Forest (unten)"
Die ersten beiden Zeilen sollten identisch mit der Visualisierung aus Kapitel 055 sein - nur die dritte Zeile (Random Forest) kommt neu hinzu.
Fußnoten
Dass der gebootsrapte Datensatz genau so groß ist wie der Datensatz, aus dem gebootstrapt wurde, ist kein muss. Scikit-Learn macht es aber standardmäßig so.↩︎
Also vergleichbar mit dem System bei einer Präsidentschaftswahl in den USA - egal wie wie knapp das Ergebnis innerhalb eines Staates ist, der Staat (also alle seine Wahlmänner) geht nur an den Sieger.↩︎
Also (mit Auge zudrücken) vergleichbar mit dem Eurovision Song Contest, wo nicht nur gezählt wird welche Länder für einen Song stimmen, sondern auch wie viele Punkte sie vergeben (1-12 Punkte). Die finale Wertung berücksichtigt sowohl die Anzahl der Stimmen als auch deren Gewichtung.↩︎