import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split, cross_val_score, RepeatedStratifiedKFold
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler
np.random.seed(42)K-Nearest Neighbors
Nachdem wir mit Random Forest und Gradient Boosting einige der fortgeschrittensten Ensemble-Methoden kennengelernt haben, wollen wir nun einen Schritt zurück machen und uns einer überraschend einfachen, aber dennoch mächtigen Klassifikationsmethode zuwenden: K-Nearest Neighbors (kNN).
Im Gegensatz zu Decision Trees, die regelbasierte Entscheidungen treffen, oder zur logistischen Regression, die eine mathematische Funktion lernt, verfolgt kNN einen völlig anderen Ansatz: Es macht Vorhersagen basierend auf der “Nachbarschaft” von Datenpunkten. Die Grundidee ist verblüffend einfach - wenn man wissen möchte, zu welcher Klasse ein neuer Datenpunkt gehört, schaut man sich einfach eine bestimmte Anzahl (\(k\)) der nächstgelegenen bekannten Datenpunkte an und lässt sie “abstimmen”.
Diese intuitive Herangehensweise macht kNN zu einer der verständlichsten Machine Learning Methoden überhaupt. Gleichzeitig bringt sie aber auch ganz neue Herausforderungen mit sich, die wir bisher nicht hatten - z.B. beim Umgang mit unterschiedlich skalierten Features.
Die Daten: Adelie vs. Gentoo Pinguine
Für dieses Kapitel nutzen wir wieder unser bewährtes Setup mit Palmer Penguins. Wir konzentrieren uns auf die binäre Klassifikation zwischen Adelie und Gentoo Pinguinen und verwenden zunächst zwei numerische Features: body_mass_g und flipper_length_mm.
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
# Nur Adelie und Gentoo auswählen
penguins_binary = penguins[penguins['species'].isin(['Adelie', 'Gentoo'])].copy()
penguins_binary = penguins_binary.dropna(subset=['body_mass_g', 'flipper_length_mm'])
# Binäre Zielvariable erstellen (0 = Adelie, 1 = Gentoo)
penguins_binary['species_binary'] = (penguins_binary['species'] == 'Gentoo').astype(int)
# Features und Ziel definieren
X = penguins_binary[["body_mass_g", "flipper_length_mm"]].values
y = penguins_binary["species_binary"].values
# Train-Test Split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
print(f"Trainingsdaten: {len(X_train)} Pinguine")
print(f"Testdaten: {len(X_test)} Pinguine")
print(f"Features: body_mass_g und flipper_length_mm")Trainingsdaten: 205 Pinguine
Testdaten: 69 Pinguine
Features: body_mass_g und flipper_length_mmFeature Scaling: Ein neuer wichtiger Schritt
Bevor wir uns mit kNN beschäftigen können, müssen wir ein Problem lösen, das bei unseren bisherigen Algorithmen nie aufgetreten ist: unterschiedlich skalierte Features.
Schauen wir uns die Wertebereiche unserer Features an:
print("Wertebereiche unserer Features:")
print(f"body_mass_g: {X_train[:, 0].min():.1f} bis {X_train[:, 0].max():.1f} (Spannweite: {X_train[:, 0].max() - X_train[:, 0].min():.1f})")
print(f"flipper_length_mm: {X_train[:, 1].min():.1f} bis {X_train[:, 1].max():.1f} (Spannweite: {X_train[:, 1].max() - X_train[:, 1].min():.1f})")Wertebereiche unserer Features:
body_mass_g: 2850.0 bis 6300.0 (Spannweite: 3450.0)
flipper_length_mm: 172.0 bis 231.0 (Spannweite: 59.0)Das Problem wird sofort deutlich: body_mass_g bewegt sich im Bereich von etwa 2700-6300g (Spannweite ~3600), während flipper_length_mm nur zwischen 172-231mm liegt (Spannweite ~59).
Warum ist das bei kNN problematisch? Wir wissen zwar noch nicht wie, aber kNN basiert die Entscheidungen welche Datenpunkte dicht beieinander liegen auf den Distanzen zwischen Datenpunkten. Der Algorithmus versteht aber natürlich keine Einheiten. Ein Unterschied von 100g im Körpergewicht hat einen viel größeren Einfluss auf die Distanz als ein Unterschied von 10mm in der Flossenlänge - obwohl beide für die Klassifikation gleich wichtig sein könnten. Der kNN-Algorithmus nimmt also einfach rohe Zahlenwerte entgegen und kann nicht einordnen ob ein Unterschied von 1g mehr oder weniger relevant ist als ein Unterschied von 1mm - für ihn sind beide gleich.
Dieses Problem hatten wir bisher bei keiner der eingeführten Klassifikationsalgorithmen, sodass wir bisher auch nie etwas dagegen unternommen haben.
Standardisierung als Lösung
Die Lösung ist Feature Scaling - wir transformieren alle Features so, dass sie auf derselben Skala liegen. Eine häufig verwendete Methode ist die Standardisierung (auch Z-Score-Normalisierung genannt):
\[z = \frac{x - \mu}{\sigma}\]
Dabei wird jedes Feature so transformiert, dass es einen Mittelwert von 0 und eine Standardabweichung von 1 hat.
# Feature Scaling mit StandardScaler
scaler = StandardScaler()
# Wichtig: Scaler nur auf Trainingsdaten anpassen!
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test) # Transformation mit den Trainingsdaten-Parametern
print("Nach der Standardisierung:")
print(f"body_mass_g (scaled) - Mittelwert: {X_train_scaled[:, 0].mean():.3f}, Std: {X_train_scaled[:, 0].std():.3f}")
print(f"flipper_length_mm (scaled) - Mittelwert: {X_train_scaled[:, 1].mean():.3f}, Std: {X_train_scaled[:, 1].std():.3f}")Nach der Standardisierung:
body_mass_g (scaled) - Mittelwert: 0.000, Std: 1.000
flipper_length_mm (scaled) - Mittelwert: -0.000, Std: 1.000Jetzt haben beide Features Mittelwert 0 und Standardabweichung 1 - sie sind auf derselben Skala und können faire Beiträge zur Distanzberechnung leisten.
Wichtig: Der Scaler wird nur auf den Trainingsdaten angepasst (fit_transform()), die Testdaten werden dann aber mit den gleichen Parametern transformiert (transform()). Würde man den Scaler auf alle Daten anpassen, hätte man Information aus den Testdaten für die Transformation genutzt - ein klassischer Fall von Data Leakage!
K-Nearest Neighbors: Das Grundkonzept
Jetzt können wir uns dem eigentlichen kNN-Algorithmus zuwenden. Die Idee ist bestechend einfach:
- Distanzen berechnen: Für einen neuen Datenpunkt (Testdaten) berechne die Distanz zu allen Punkten im Trainingsdatensatz
- Nachbarn finden: Identifiziere die k nächsten Nachbarn, wobei k irgendeine Anzahl ist.
- Abstimmen lassen: Die Mehrheit dieser k Nachbarn bestimmt die vorhergesagte Klasse
Beginnen wir mit einem einfach mal mit k=3:
# K-Nearest Neighbors mit k=3 für didaktische Zwecke
knn_3 = KNeighborsClassifier(n_neighbors=3)
knn_3.fit(X_train_scaled, y_train);
# Performance bewerten
y_pred_train_3 = knn_3.predict(X_train_scaled)
y_pred_test_3 = knn_3.predict(X_test_scaled)
train_acc_3 = accuracy_score(y_train, y_pred_train_3)
test_acc_3 = accuracy_score(y_test, y_pred_test_3)
print(f"K-Nearest Neighbors (k=3) Performance:")
print(f" Training Accuracy: {train_acc_3:.4f}")
print(f" Test Accuracy: {test_acc_3:.4f}")
print(f" Overfitting: {(train_acc_3-test_acc_3):.4f}")K-Nearest Neighbors (k=3) Performance:
Training Accuracy: 0.9902
Test Accuracy: 1.0000
Overfitting: -0.0098Visualisierung der Nachbarschaftsbeziehungen
Um das Konzept zu verdeutlichen, schauen wir uns an, wie kNN Entscheidungen trifft. Wir definieren drei spezielle fiktive Testpunkte und visualisieren für jeden seine nächsten Nachbarn.
In der folgenden Abbildung bedeuten die verschiedenen Elemente:
-
Orange Punkte: Adelie Pinguine (Trainingsdaten)
- Türkisfarbene Punkte: Gentoo Pinguine (Trainingsdaten)
- Sterne mit schwarzem Rand: Die drei Testpunkte, gefärbt nach der kNN-Vorhersage
- Rote Kreise: Die jeweils 3 nächsten Nachbarn eines Testpunkts
- Gestrichelte rote Linien: Distanzen zwischen Testpunkt und seinen Nachbarn
- Rote Rechtecke: Zoom-Bereiche, die in den Detail-Plots vergrößert dargestellt werden
# Drei spezielle Testpunkte definieren
test_points_coords = [
(-1, -1), # Im Adelie-Bereich
(0.1, 0.2), # An der Grenze
(1, 0) # Im Gentoo-Bereich
]Code zeigen/verstecken
# 2×2 Layout: Übersicht + 3 Detail-Ansichten
fig, axes = plt.subplots(2, 2, figsize=(10, 6), layout='tight')
axes = axes.flatten()
# Masken für die beiden Klassen
adelie_mask = y_train == 0
gentoo_mask = y_train == 1
# Zuerst alle Zoom-Bereiche berechnen für die Übersicht
zoom_rectangles = []
test_points_data = []
for test_coords in test_points_coords:
test_point = np.array(test_coords).reshape(1, -1)
distances, indices = knn_3.kneighbors(test_point, n_neighbors=3)
nearest_neighbors = X_train_scaled[indices[0]]
neighbor_labels = y_train[indices[0]]
prediction = knn_3.predict(test_point)[0]
# Zoom-Bereich berechnen
all_points = np.vstack([test_point, nearest_neighbors])
margin = 0.1
x_min = all_points[:, 0].min() - margin
x_max = all_points[:, 0].max() + margin
y_min = all_points[:, 1].min() - margin
y_max = all_points[:, 1].max() + margin
zoom_rectangles.append((x_min, x_max, y_min, y_max))
test_points_data.append({
'coords': test_coords,
'point': test_point,
'distances': distances,
'indices': indices,
'neighbors': nearest_neighbors,
'neighbor_labels': neighbor_labels,
'prediction': prediction
})
# Subplot 1: Übersicht mit allen Testpunkten und Zoom-Bereichen
ax = axes[0]
ax.scatter(X_train_scaled[adelie_mask, 0], X_train_scaled[adelie_mask, 1],
c=colors['Adelie'], alpha=0.9, s=50, label='Adelie (Training)')
ax.scatter(X_train_scaled[gentoo_mask, 0], X_train_scaled[gentoo_mask, 1],
c=colors['Gentoo'], alpha=0.9, s=50, label='Gentoo (Training)')
# Alle drei Testpunkte in der Übersicht
for i, data in enumerate(test_points_data):
predicted_species = 'Gentoo' if data['prediction'] == 1 else 'Adelie'
point_color = colors[predicted_species]
ax.scatter(data['point'][0, 0], data['point'][0, 1],
c=point_color, s=150, marker='*', edgecolor='black', linewidth=2,
label=f'Testpunkt {i+1}: {data["coords"]}' if i < 3 else "")
# Zoom-Bereiche als rote Rechtecke einzeichnen
for i, (x_min, x_max, y_min, y_max) in enumerate(zoom_rectangles):
from matplotlib.patches import Rectangle
rect = Rectangle((x_min, y_min), x_max - x_min, y_max - y_min,
linewidth=2, edgecolor='red', facecolor='none', alpha=0.8)
ax.add_patch(rect)
# Nummer des Zoom-Bereichs
ax.text(x_min, y_max + 0.05, f'{i+1}', fontsize=12, color='red',
fontweight='bold', ha='left')
ax.set_ylabel('flipper_length_mm (standardisiert)');
ax.set_title('Übersicht');
ax.grid(True, alpha=0.3);
# Subplots 2-4: Detail-Ansichten für jeden Testpunkt
for i, (ax, data) in enumerate(zip(axes[1:], test_points_data)):
# Linien zu den nächsten Nachbarn zeichnen (ganz hinten)
for j, neighbor in enumerate(data['neighbors']):
ax.plot([data['point'][0, 0], neighbor[0]], [data['point'][0, 1], neighbor[1]],
'r--', alpha=0.7, linewidth=2, zorder=1)
# Alle Trainingspunkte (schwächer dargestellt)
ax.scatter(X_train_scaled[adelie_mask, 0], X_train_scaled[adelie_mask, 1],
c=colors['Adelie'], alpha=0.9, s=30, label='Adelie (Training)', zorder=2)
ax.scatter(X_train_scaled[gentoo_mask, 0], X_train_scaled[gentoo_mask, 1],
c=colors['Gentoo'], alpha=0.9, s=30, label='Gentoo (Training)', zorder=2)
# Nächste Nachbarn hervorheben
ax.scatter(data['neighbors'][:, 0], data['neighbors'][:, 1],
s=120, facecolors='none', edgecolors='red', linewidth=3,
label='3 nächste Nachbarn', zorder=3)
# Testpunkt hervorheben (ganz vorne)
predicted_species = 'Gentoo' if data['prediction'] == 1 else 'Adelie'
point_color = colors[predicted_species]
ax.scatter(data['point'][0, 0], data['point'][0, 1],
c=point_color, s=400, marker='*', edgecolor='black', linewidth=2,
label=f'Testpunkt (Vorhersage: {predicted_species})', zorder=4)
# Distanz als Text anzeigen (ganz vorne)
for j, neighbor in enumerate(data['neighbors']):
mid_x = (data['point'][0, 0] + neighbor[0]) / 2
mid_y = (data['point'][0, 1] + neighbor[1]) / 2
ax.text(mid_x, mid_y, f'{data["distances"][0][j]:.2f}',
bbox=dict(boxstyle="round,pad=0.3", facecolor="white", alpha=0.9),
fontsize=9, ha='center', zorder=5)
# Zoom-Bereich setzen
x_min, x_max, y_min, y_max = zoom_rectangles[i]
ax.set_xlim(x_min, x_max)
ax.set_ylim(y_min, y_max)
# Achsentitel nur für die äußeren Subplots
if i == 1: # unten links
ax.set_ylabel('flipper_length_mm (std.)')
ax.set_xlabel('body_mass_g (std.)')
elif i == 2: # unten rechts
ax.set_xlabel('body_mass_g (std.)')
ax.set_title(f'Detail {i+1}: Testpunkt {data["coords"]}')
ax.grid(True, alpha=0.3);
# Voting-Details ausgeben
neighbor_species = ['Gentoo' if label == 1 else 'Adelie' for label in data['neighbor_labels']]
adelie_votes = neighbor_species.count('Adelie')
gentoo_votes = neighbor_species.count('Gentoo')
print(f"\nTestpunkt {data['coords']}:")
print(f" Nächste Nachbarn: {neighbor_species}")
print(f" Abstimmung: {adelie_votes} × Adelie, {gentoo_votes} × Gentoo")
print(f" Vorhersage: {predicted_species}")
plt.show()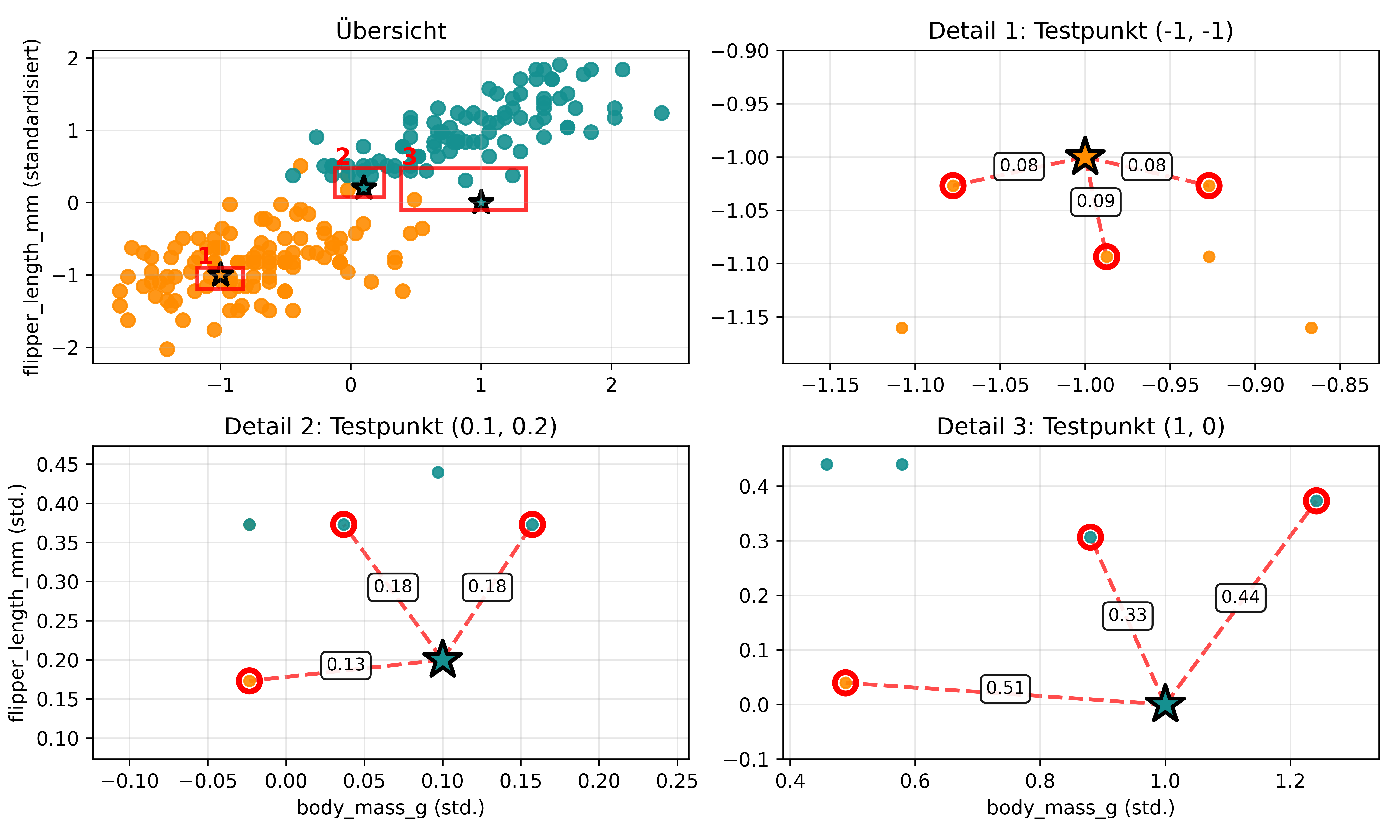
Diese Visualisierung macht das kNN-Prinzip sehr deutlich: Der Algorithmus “fragt” die dichtesten Nachbarn zu welcher Klasse sie gehören und entscheidet basierend auf der Mehrheit zu welcher Klasse dann der neue Punkt gehören sollte.
Klassifikationsgrenzen visualisieren
Nutzen wir nun unsere bewährte plot_classifier() Funktion (mit proba=True; siehe Kapitel 5.5), um zu sehen, wie kNN Klassifikationsgrenzen zieht. Die Hintergrundfarbe zeigt, wie der Algorithmus an jedem Punkt des Feature-Raums entscheiden würde - basierend auf der Abstimmung der 3 nächsten Nachbarn.
Da bei k=3 nur vier verschiedene Abstimmungsergebnisse möglich sind (3-0, 2-1, 1-2, 0-3), sehen wir im Hintergrund entsprechend vier verschiedene Farbintensitäten: Bei einstimmigen Entscheidungen erhalten wir die klaren Farben (orange für Adelie, türkis für Gentoo), während knappe 2-1 Entscheidungen in abgeschwächteren Farbtönen dargestellt werden.
Diese Farbabstufungen spiegeln auch die “Wahrscheinlichkeiten” wider, die durch proba=True ausgegeben werden. Allerdings sind das bei kNN - ähnlich wie bei Decision Trees - keine Wahrscheinlichkeiten im strengen statistischen Sinne, sondern vielmehr die empirischen Abstimmungsergebnisse der Nachbarn. Eine “Wahrscheinlichkeit” von 0.67 bedeutet bei k=3 beispielsweise, dass 2 von 3 Nachbarn für diese Klasse gestimmt haben.
Code zeigen/verstecken
def plot_classifier(model, X_train, y_train, X_test, y_test,
proba=False, xlabel=None, ylabel=None, title=None,
class_colors=None, figsize=(12, 5), axes=None):
"""
Visualisiert Klassifikationsgrenzen für ein trainiertes Modell
Parameter:
- model: Trainiertes sklearn Klassifikationsmodell
- X_train, y_train: Trainingsdaten (Features und Labels)
- X_test, y_test: Testdaten (Features und Labels)
- proba: Bool, ob Wahrscheinlichkeiten (True) oder Klassen (False) gezeigt werden
- xlabel, ylabel: Achsenbeschriftungen
- title: Titel der Abbildung
- class_colors: Dictionary mit Farben für die Klassen {0: 'farbe1', 1: 'farbe2'}
- figsize: Größe der Abbildung als Tuple (width, height)
- axes: Optionales Tupel oder Liste mit zwei matplotlib-Achsenobjekten – wenn angegeben, wird in diese gezeichnet
"""
# Subplot-Layout erstellen: 1 Zeile, 2 Spalten (nur falls keine Achsen übergeben wurden)
if axes is None:
fig, axes = plt.subplots(1, 2, figsize=figsize, sharex=True, sharey=True, layout='tight')
own_fig = True
else:
own_fig = False
# Standard-Farben (Rot & Blau) verwenden, falls keine angegeben
if class_colors is None:
class_colors = {0: 'red', 1: 'blue'}
# Custom Colormap für den Hintergrund erstellen
# Von Klasse 0 (z.B. orange) über weiß zu Klasse 1 (z.B. türkis)
gradient_colors = [class_colors[0], 'white', class_colors[1]]
custom_cmap = LinearSegmentedColormap.from_list("CustomDiverging", gradient_colors, N=256)
# Gemeinsame Grenzen für beide Plots berechnen
# Alle Daten (Training + Test) kombinieren um einheitliche Achsen zu haben
X_all = np.vstack([X_train, X_test])
x_margin = (X_all[:, 0].max() - X_all[:, 0].min()) * 0.05 # 5% Rand
y_margin = (X_all[:, 1].max() - X_all[:, 1].min()) * 0.05 # 5% Rand
x_min = X_all[:, 0].min() - x_margin
x_max = X_all[:, 0].max() + x_margin
y_min = X_all[:, 1].min() - y_margin
y_max = X_all[:, 1].max() + y_margin
# Meshgrid für Hintergrund-Vorhersagen erstellen
# 1000x1000 Grid für glatte Darstellung
xx, yy = np.meshgrid(
np.linspace(x_min, x_max, 1000),
np.linspace(y_min, y_max, 1000)
)
# Vorhersagen für jeden Punkt im Grid
if proba:
# Wahrscheinlichkeiten für Klasse 1
zz = model.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1].reshape(xx.shape)
else:
# Klassenlabels (0 oder 1)
zz = model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
# Beide Subplots (Training und Test) erstellen
for ax, X, y, subset in zip(axes, [X_train, X_test], [y_train, y_test],
["Trainingsdaten", "Testdaten"]):
# Vorhersagen für die aktuellen Daten
y_pred = model.predict(X)
# Hintergrund mit Klassifikationsgrenzen zeichnen
if proba:
# Kontinuierliche Wahrscheinlichkeiten als Heatmap
ax.imshow(zz, origin="lower", aspect="auto",
extent=(x_min, x_max, y_min, y_max),
vmin=0, vmax=1, alpha=0.25, cmap=custom_cmap)
else:
# Diskrete Klassengrenzen
ax.contourf(xx, yy, zz,
alpha=0.25,
vmin=0, vmax=1,
levels=[-0.5, 0.5, 1.5], # Grenzen für Klasse 0 und 1
colors=[class_colors[0], class_colors[1]])
# Datenpunkte zeichnen
# Gesichtsfarbe basiert auf wahrer Klasse
face_colors = [class_colors[int(label)] for label in y]
# Randfarbe zeigt richtige (schwarz) vs. falsche (rot) Vorhersagen
edge_colors = ['black' if true_label == pred_label else 'red'
for true_label, pred_label in zip(y, y_pred)]
ax.scatter(X[:, 0], X[:, 1],
c=face_colors,
edgecolor=edge_colors,
linewidth=1,
s=50)
# Subplot-Eigenschaften setzen
ax.set_title(subset)
ax.set_xlim(x_min, x_max)
ax.set_ylim(y_min, y_max)
if xlabel:
ax.set_xlabel(xlabel)
if ylabel:
ax.set_ylabel(ylabel)
# Gesamttitel und Anzeige nur, wenn eigene Figure erzeugt wurde
if own_fig:
if title:
fig.suptitle(title, fontsize=14)
plt.show()
# KNN Klassifikationsgrenzen visualisieren
plot_classifier(
model=knn_3,
X_train=X_train_scaled,
y_train=y_train,
X_test=X_test_scaled,
y_test=y_test,
proba=True,
title="K-Nearest Neighbors (k=3) - Klassifikationsgrenzen",
xlabel="body_mass_g (standardisiert)",
ylabel="flipper_length_mm (standardisiert)",
class_colors={0: colors['Adelie'], 1: colors['Gentoo']}
)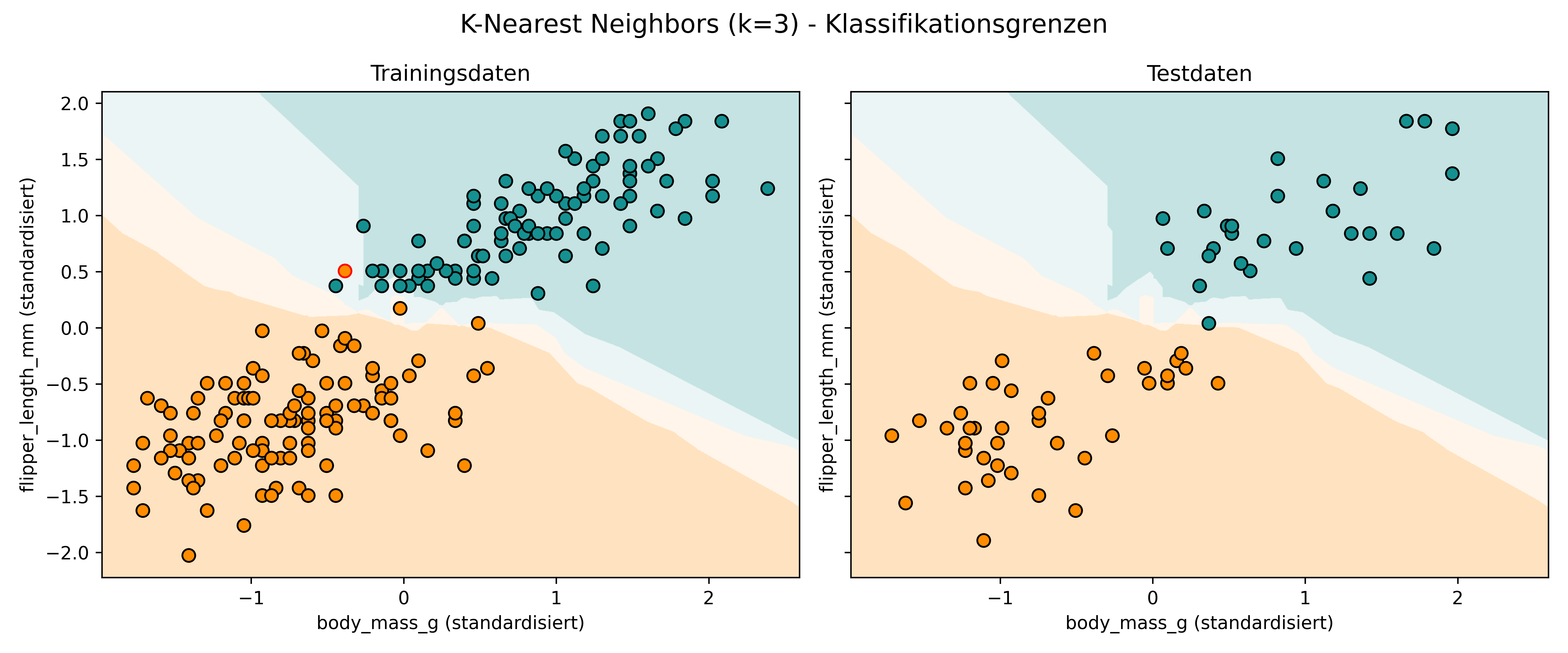
Die kNN-Klassifikationsgrenzen unterscheiden sich stark von dem, was wir bisher gesehen haben:
- Organische Formen: Im Gegensatz zu den geraden Linien der logistischen Regression oder den rechteckigen Bereichen der Decision Trees entstehen bei kNN natürlich wirkende, curved Klassifikationsgrenzen
- Lokale Anpassung: Die Grenzen passen sich sehr flexibel an die lokale Datenverteilung an
- Voronoi-ähnliche Struktur: Die Bereiche um die Datenpunkte erinnern an Voronoi-Diagramme
Die Wahl von k: Overfitting vs. Underfitting
Ein kritischer Parameter bei kNN ist die Wahl von k. Schauen wir uns an, wie sich verschiedene k-Werte auswirken:
# Verschiedene k-Werte testen
k_values = [1, 2, 3, 4, 5, 10, 25, 50, 75, 100, 125, 150, 175, len(X_train)] # Von sehr klein bis Datensatzgröße
results = []
for k in k_values:
if k > len(X_train):
continue
knn = KNeighborsClassifier(n_neighbors=k)
knn.fit(X_train_scaled, y_train);
train_acc = accuracy_score(y_train, knn.predict(X_train_scaled))
test_acc = accuracy_score(y_test, knn.predict(X_test_scaled))
results.append({
'k': k,
'Training Accuracy': train_acc,
'Test Accuracy': test_acc,
'Overfitting': train_acc - test_acc
})
# Ergebnisse anzeigen
results_df = pd.DataFrame(results)
print("Performance für verschiedene k-Werte:")
print(results_df.to_string(index=False, float_format='%.4f'))KNeighborsClassifier(n_neighbors=205)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| n_neighbors | 205 | |
| weights | 'uniform' | |
| algorithm | 'auto' | |
| leaf_size | 30 | |
| p | 2 | |
| metric | 'minkowski' | |
| metric_params | None | |
| n_jobs | None |
Performance für verschiedene k-Werte:
k Training Accuracy Test Accuracy Overfitting
1 0.9951 0.9855 0.0096
2 0.9902 0.9855 0.0047
3 0.9902 1.0000 -0.0098
4 0.9902 1.0000 -0.0098
5 0.9805 1.0000 -0.0195
10 0.9805 1.0000 -0.0195
25 0.9805 1.0000 -0.0195
50 0.9805 1.0000 -0.0195
75 0.9756 1.0000 -0.0244
100 0.9854 1.0000 -0.0146
125 0.9756 1.0000 -0.0244
150 0.9610 0.9855 -0.0245
175 0.9512 0.9855 -0.0343
205 0.5463 0.5652 -0.0189# Visualisierung der k-Wert Auswirkungen
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
ax.plot(results_df['k'], results_df['Training Accuracy'], 'o-', label='Training Accuracy', color='blue', alpha=0.7);
ax.plot(results_df['k'], results_df['Test Accuracy'], 'o-', label='Test Accuracy', color='red', alpha=0.7);
ax.set_xlabel('k (Anzahl Nachbarn)');
ax.set_ylabel('Accuracy');
ax.set_title('Auswirkung verschiedener k-Werte auf die Performance');
ax.legend();
ax.grid(True, alpha=0.3);
# Optimales k hervorheben
best_k = results_df.loc[results_df['Test Accuracy'].idxmax(), 'k']
best_test_acc = results_df.loc[results_df['Test Accuracy'].idxmax(), 'Test Accuracy']
ax.axvline(x=best_k, color='green', linestyle='--', alpha=0.7, label=f'Optimales k={best_k}');
plt.show()
print(f"\nOptimales k: {best_k} (Test Accuracy: {best_test_acc:.4f})")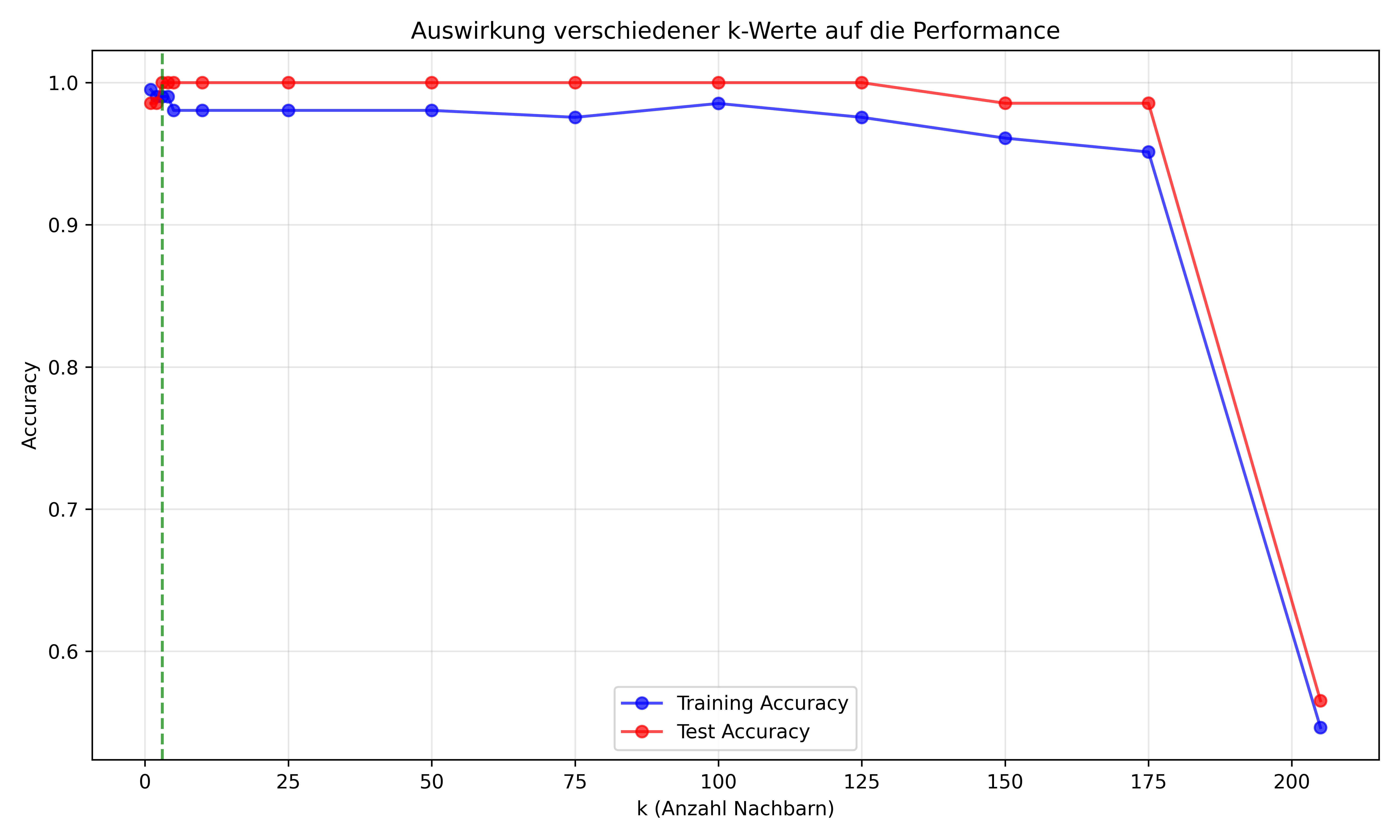
Optimales k: 3 (Test Accuracy: 1.0000)Die Ergebnisse zeigen ein bekanntes Muster zwischen Overfitting und Underfitting:
- Kleine k-Werte (z.B. k=1): Das Modell wird sehr flexibel und passt sich stark an die Trainingsdaten an → Overfitting
- Große k-Werte (z.B. k=Datensatzgröße): Das Modell wird zu starr und kann wichtige Muster nicht erfassen → Underfitting
- Optimales k: Balanciert zwischen diesen Extremen für beste Generalisierung auf neue Daten
Visualisierung verschiedener k-Werte
Um die Auswirkungen verschiedener k-Werte zu verdeutlichen, schauen wir uns die Klassifikationsgrenzen für vier repräsentative Werte an:
Code zeigen/verstecken
# Vier verschiedene kNN-Modelle mit unterschiedlichen k-Werten trainieren
k_comparison = [1, 5, 100, 205]
knn_models = {}
for k in k_comparison:
knn_models[k] = KNeighborsClassifier(n_neighbors=k)
knn_models[k].fit(X_train_scaled, y_train);
# 4×2 Visualisierung: Vier verschiedene k-Werte untereinander
fig, axes = plt.subplots(4, 2, figsize=(14, 20), layout='tight', sharex=True, sharey=True)
# Für jeden k-Wert eine Zeile erstellen
for i, k in enumerate(k_comparison):
plot_classifier(
model=knn_models[k],
X_train=X_train_scaled,
y_train=y_train,
X_test=X_test_scaled,
y_test=y_test,
proba=True,
xlabel="body_mass_g (standardisiert)" if i == 3 else "", # Nur bei unterster Zeile
ylabel="flipper_length_mm (standardisiert)" if i == 0 or i == 1 or i == 2 or i == 3 else "",
class_colors={0: colors['Adelie'], 1: colors['Gentoo']},
axes=axes[i, :] # i-te Zeile, beide Spalten
)
# Titel für jede Zeile hinzufügen
axes[i, 0].set_ylabel(f'k={k}\nflipper_length_mm (std.)', fontsize=12);
plt.show()
# Performance-Vergleich für diese vier k-Werte
print("Performance-Vergleich für die visualisierten k-Werte:")
for k in k_comparison:
train_acc = accuracy_score(y_train, knn_models[k].predict(X_train_scaled))
test_acc = accuracy_score(y_test, knn_models[k].predict(X_test_scaled))
print(f"k={k:3d}: Training Accuracy: {train_acc:.4f}, Test Accuracy: {test_acc:.4f}")
Performance-Vergleich für die visualisierten k-Werte:
k= 1: Training Accuracy: 0.9951, Test Accuracy: 0.9855
k= 5: Training Accuracy: 0.9805, Test Accuracy: 1.0000
k=100: Training Accuracy: 0.9854, Test Accuracy: 1.0000
k=205: Training Accuracy: 0.5463, Test Accuracy: 0.5652Die Visualisierung macht die konzeptionellen Unterschiede zwischen den k-Werten deutlich:
- k=1: Sehr komplexe, “zackige” Entscheidungsgrenzen mit vielen kleinen Regionen. Jeder Trainigspunkt hat seinen eigenen kleinen Einflussbereich. Es gibt nur die Ergebnisse 1-0 und 0-1. Perfekte Training Accuracy, aber schlechte Generalisierung.
- k=5: Etwas glattere Grenzen als vorhin bei k=3. Immerhin gibt es jetzt seches mögliche Ergebnisse: 5-0, 4-1, 3-2, 2-3, 1-4 und 0-5.
- k=100: Deutlich glattere Entscheidungsgrenzen.
- k=205: Unsinnige Anwednung. Da 205 der gesamten Datensatzgröße entspricht, ist der Hintergrund weiß, also die Vorhersage sehr unsicher. Tatsächlich werden so ja immer alle vorhandenen Punkte als dichteste Nachbarn angesehen, sodass kein Nachbar als nicht-dicht-genug gilt - egal wo der zu klassifizierende Punkt liegt. Die Accuracy ist einfach so genau, wie sie eben ist wenn man alle Punkte immer als die Klasse klassifiziert, die am häufigsten in den Trainingsdaten auftaucht.
Erweiterung auf den generellen Fall
Bisher haben wir nur genau zwei numerische Features verwendet, sodass sich alles super intuitiv visualisieren ließ und auch die Distanzen zwischen Punkten nicht wirklich erklärungsbedürftig waren (auch wenn wir noch immer nicht darüber gesprochen haben wie diese Distanzen eigentlich berechnet werden).
Es gilt demnach sowohl auf den Fall mit kategorialen Features, als auch generell mehr Features zu erweitern.
Kategoriale Variablen: Dummy-Codierung
Wie geht kNN also mit kategorialen Variablen um? Kurz gesagt: So wie z.B. Decision Trees auch, nämlich indem mittels Dummy-Codierung (1/0) eben doch quasi-metrische Werte erzeugt werden. Und auch diese werden dann noch vorher standardisiert, sodass sie nicht mehr 1 und 0 sind. Wir können sogar mal solch eine dummy-codierte Variable in unseren plot_classifier() nehmen:
# Datensatz mit kategoriale Variable erweitern
penguins_with_island = penguins[penguins['species'].isin(['Adelie', 'Gentoo'])].copy()
penguins_with_island = penguins_with_island.dropna(subset=['body_mass_g', 'island'])
# One-Hot-Encoding für island
penguins_encoded = pd.get_dummies(penguins_with_island, columns=['island'], prefix='island')
# Nur zwei Features für bessere Visualisierung
feature_cols_vis = ['island_Dream', 'body_mass_g']
X_cat_vis = penguins_encoded[feature_cols_vis]
y_cat_vis = (penguins_encoded['species'] == 'Gentoo').astype(int)
# Train-Test Split für Visualisierung
X_vis_train, X_vis_test, y_vis_train, y_vis_test = train_test_split(
X_cat_vis, y_cat_vis, test_size=0.25, random_state=42, stratify=y_cat_vis
)
print("Vor Standardisierung:")
print(X_vis_train.head())
# Scaling und Training
scaler_vis = StandardScaler()
X_vis_train_scaled = scaler_vis.fit_transform(X_vis_train)
X_vis_test_scaled = scaler_vis.transform(X_vis_test)
print("\nNach Standardisierung:")
print(pd.DataFrame(X_vis_train_scaled, columns=feature_cols_vis).head())
knn_vis = KNeighborsClassifier(n_neighbors=5)
knn_vis.fit(X_vis_train_scaled, y_vis_train);
# Visualisierung
plot_classifier(
model=knn_vis,
X_train=X_vis_train_scaled,
y_train=y_vis_train,
X_test=X_vis_test_scaled,
y_test=y_vis_test,
proba=True,
title="K-Nearest Neighbors mit island_Dream",
xlabel="island_Dream (standardisiert)",
ylabel="body_mass_g (standardisiert)",
class_colors={0: colors['Adelie'], 1: colors['Gentoo']}
)Vor Standardisierung:
island_Dream body_mass_g
44 True 3000.0
249 False 4875.0
231 False 5950.0
41 True 3900.0
137 True 3975.0
Nach Standardisierung:
island_Dream body_mass_g
0 1.940990 -1.599065
1 -0.515201 0.614460
2 -0.515201 1.883548
3 1.940990 -0.536573
4 1.940990 -0.448032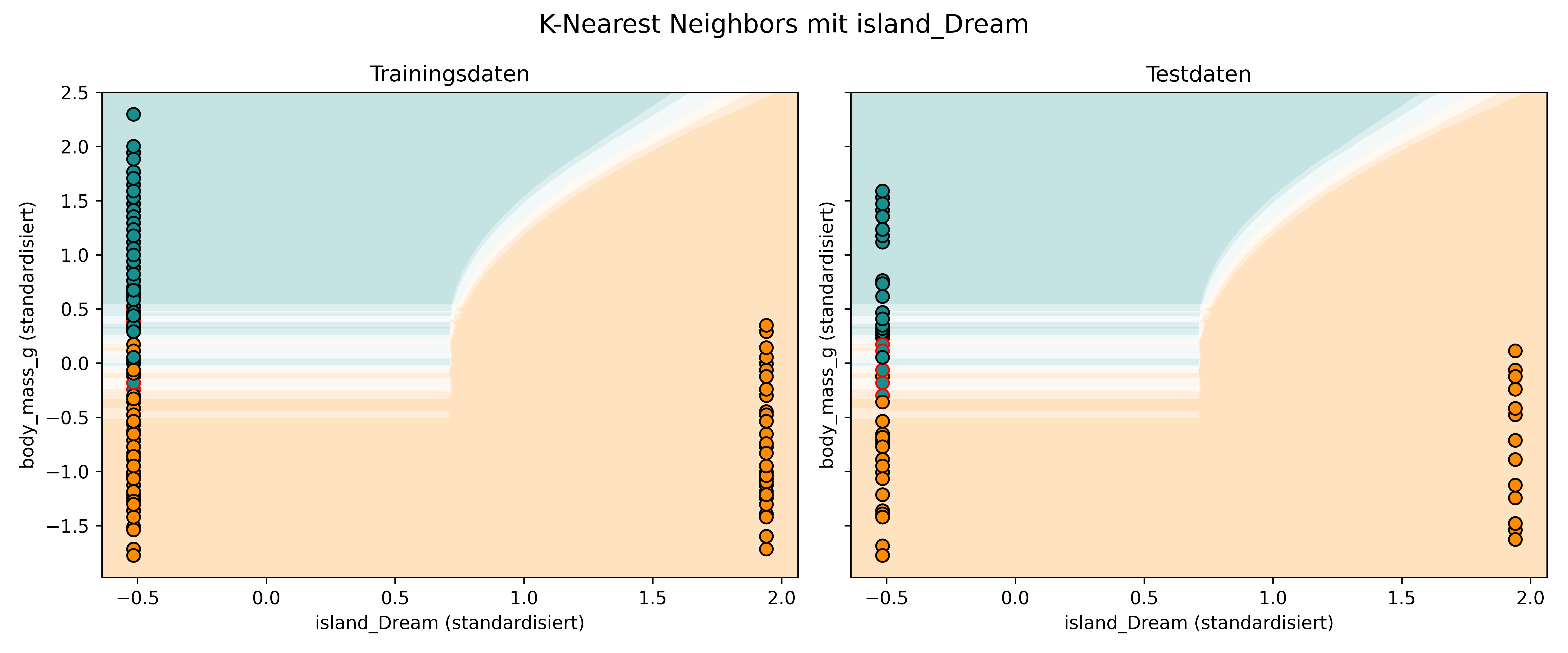
Also: Auf den ersten Blick mag es schwierig wirken, kategoriale Variablen in eine Distanzberechnung zu integrieren. Aber durch die Dummy-Codierung zu 0 und 1 funktioniert es am Ende doch ganz einfach - genau wie im obigen Beispiel zu sehen. Durch die Standardisierung sind die Distanzen zwischen 0 und 1 genauso zu werten wie Distanzen zwischen verschiedenen Gramm-Zahlen der Körpermasse.
Die Testdaten werden natürlich auch immer nur genau auf die 0 oder 1 (vor Standardisierung) fallen, aber dennoch kann mit exakt der gleichen Berechnungsmethode die Distanz zu allen anderen Punkten berechnet werden. Es ist also nur auf den ersten Blick kompliziert, aber im Endeffekt “dasselbe in Grün” wie wenn man mit metrischen Variablen arbeitet, auch wenn sich letztere natürlich viel intuitiver anfühlen.
Mehr Features - Höherdimensionale Räume
Das Schöne an kNN ist, dass das Grundprinzip auch bei mehr als 3 Features unverändert bleibt, auch wenn wir uns dann nicht mehr in einem 2- oder 3-dimensionalen Raum befinden. Ob wir 2, 3, oder 50 Features haben - die euklidische Distanzberechnung (die sklearn standardmäßig verwendet; andere folgen gleich) funktioniert mathematisch identisch:
2D: \(d = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}\)
3D: \(d = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2}\)
nD: \(d = \sqrt{\sum_{i=1}^{n}(f_{i1}-f_{i2})^2}\)
Wir können uns diese höherdimensionalen Räume zwar nicht mehr visuell vorstellen, aber das Konzept bleibt dasselbe: Finde die nächsten Nachbarn (bezogen auf alle Features gleichzeitig), lass sie abstimmen.
Distanzmetriken: Alternativen zur euklidischen Distanz
Nun sollten wir auch darüber sprechen wie denn eigentlich diese Distanz zwischen zwei Punkte berechnet wird. Standardmäßig (und in allen Beispielen dieses Kapitels) wird die euklidische Distanz verwendet. kNN unterstützt aber verschiedene Distanzmetriken für verschiedene Datentypen und Anwendungsfälle. Hier soll ein kurzer, nicht-erschöpfender Eindruck der verschiedenen Maße gegeben werden:
1. Euklidische Distanz (Standard; auch: L2-Distanz):
\[d_{euclidean} = \sqrt{\sum_{i=1}^{n}(x_i-y_i)^2}\]
- Wann nutzen: Kontinuierliche, numerische Daten
- Vorteil: Intuitiv, entspricht geometrischer Distanz
- Nachteil: Empfindlich gegenüber Ausreißern
2. Manhattan-Distanz (auch: L1-Distanz, Taxicab-Distanz):
\[d_{manhattan} = \sum_{i=1}^{n}|x_i-y_i|\]
- Wann nutzen: Bei vielen Ausreißern oder spärlichen Daten
- Vorteil: Robuster gegenüber Ausreißern
- Nachteil: Weniger intuitiv bei kontinuierlichen Daten
3. Cosinus-Distanz:
\[d_{cosine} = 1 - \frac{\sum_{i=1}^{n}x_i y_i}{\sqrt{\sum_{i=1}^{n}x_i^2} \sqrt{\sum_{i=1}^{n}y_i^2}}\]
- Wann nutzen: Hochdimensionale Daten, Textanalyse, Empfehlungssysteme
- Vorteil: Berücksichtigt nur Richtung, nicht Magnitude
- Nachteil: Nicht für alle Datentypen geeignet
4. Hamming-Distanz:
\[d_{hamming}(x, y) = \sum_{i=1}^{n} \mathbb{1}_{x_i \ne y_i}\]
- Wann nutzen: Binäre oder kategoriale Daten
- Vorteil: Optimal für diskrete Features
- Nachteil: Nur für kategoriale Daten
Der Vollständigkeit halber - und damit man die L1 und L2 Bezeichnung einordnen kann - sei gesagt: Die Minkowski-Distanz ist eine verallgemeinerte Distanzmetrik, die sowohl die euklidische als auch die Manhattan-Distanz als Spezialfälle umfasst:
\[d_{minkowski}(x, y) = \left( \sum_{i=1}^{n} |x_i - y_i|^p \right)^{1/p}\]
- Für \(p = 1\): Manhattan-Distanz (L1)
- Für \(p = 2\): Euklidische Distanz (L2)
Der Parameter \(p\) bestimmt, wie stark größere Abweichungen gewichtet werden. Viele Implementierungen von kNN erlauben die direkte Angabe von p, z.B. metric="minkowski", p=2.
Praktische Faustregeln
- Euklidische Distanz: Standard-Wahl für die meisten kontinuierlichen Daten
- Manhattan-Distanz: Bei vielen Ausreißern oder wenn Features unterschiedliche Bedeutung haben
- Cosinus-Distanz: Bei hochdimensionalen Daten (z.B. Textdaten, genetische Daten)
- Hamming-Distanz: Bei ausschließlich kategorialen Features
Hier wenden wir mal kurz alle vier an und sehen, dass es für unsere Beispieldaten keinen großen Unterschied macht - abgesehen von der Hamming Distanz, die wir hier eigentlich gar nicht hätten anwenden dürfen.
# Vergleich verschiedener Distanzmetriken
distance_metrics = ['euclidean', 'manhattan', 'cosine', 'hamming']
metric_results = []
for metric in distance_metrics:
knn_metric = KNeighborsClassifier(n_neighbors=3, metric=metric);
knn_metric.fit(X_train_scaled, y_train);
test_acc = accuracy_score(y_test, knn_metric.predict(X_test_scaled))
metric_results.append({'Metric': metric, 'Test Accuracy': test_acc})
metric_df = pd.DataFrame(metric_results)
print("Vergleich verschiedener Distanzmetriken:")
print(metric_df.to_string(index=False, float_format='%.4f'))KNeighborsClassifier(metric='hamming', n_neighbors=3)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| n_neighbors | 3 | |
| weights | 'uniform' | |
| algorithm | 'auto' | |
| leaf_size | 30 | |
| p | 2 | |
| metric | 'hamming' | |
| metric_params | None | |
| n_jobs | None |
Vergleich verschiedener Distanzmetriken:
Metric Test Accuracy
euclidean 1.0000
manhattan 1.0000
cosine 1.0000
hamming 0.9420Lazy Learning: Ein fundamentaler Unterschied
Mit kNN lernen wir zum ersten Mal einen Algorithmus kennen, der zu einer völlig anderen Kategorie gehört: Lazy Learning. Bisher kannten wir nur Eager Learning Algorithmen, deshalb ist es wichtig, diesen fundamentalen Unterschied zu verstehen.
Eager Learning (alle bisherigen Algorithmen): Bei der simplen linearen Regression beispielsweise können wir eine Million Datenpunkte haben, auf die das Modell angepasst wird. Dieser Learning/Trainings-prozess kann durchaus aufwändig und zeitintensiv sein - schließlich müssen die optimalen Parameter (Achsenabschnitt und Steigung) gefunden werden. Aber sobald das Training abgeschlossen ist, haben wir ein sehr kompaktes Modell mit nur zwei Parametern.
Jede neue Vorhersage ist dann blitzschnell: Wir setzen einfach den x-Wert in die Gleichung \(y = mx + b\) ein - fertig! Egal ob wir 1 oder 100.000 Vorhersagen machen, jede einzelne erfordert nur diese simple Berechnung mit zwei Zahlen.
Lazy Learning (kNN): Bei kNN ist alles genau umgekehrt. Das “Learning/Training” ist praktisch nicht existent - der Algorithmus speichert einfach alle Trainingsdaten ab, ohne irgendetwas zu berechnen oder zu lernen. Streng genommen gibt es nicht einmal ein “Modell” im klassischen Sinne.
Die eigentliche Arbeit passiert erst bei jeder einzelnen Vorhersage: Für jeden neuen Testpunkt müssen die Distanzen zu allen Trainingspunkten berechnet werden. Bei einer Million Trainingspunkte bedeutet das eine Million Distanzberechnungen pro Vorhersage. Erst danach können wir schauen, welche k Distanzen am kleinsten sind.
Das Entscheidende ist: Diese Berechnungen sind “weggeschmissen”, sobald wir den nächsten Testpunkt klassifizieren wollen. Keine einzige der eben berechneten Distanzen ist noch brauchbar - wir müssen für den neuen Punkt wieder alle Distanzen zu allen Trainingspunkten neu berechnen.
Deshalb heißt es “lazy” - der Algorithmus ist “faul” beim Training (macht praktisch nichts), muss aber bei jeder Vorhersage die volle Arbeit leisten. Bei eager learning ist es umgekehrt: harte Arbeit beim Training, aber dann sehr effiziente Vorhersagen.
Curse of Dimensionality
Ein wichtiges Problem von kNN zeigt sich erst bei vielen Features: der Curse of Dimensionality. In niedrigdimensionalen Räumen (2-3 Features) haben Datenpunkte klar unterscheidbare Nachbarn - manche sind nah, andere weit entfernt. Aber je mehr Features wir hinzufügen, desto mehr “verwischen” diese Distanzunterschiede.
Um diesen Effekt zu verstehen, können wir ihn mal völlig losgelöst von unseren Pinguindaten anhand eines kleinen Codebeispiels demonstrieren. Wir erzeugen einfach 100 Features mit immer 1000 zufälligen, normalverteilten Punkte. Diese 100 Features haben natürlich jeweils andere zufälle Werte, aber alle sind eben immer normalverteilt mit einem Mittelwert 0 und einer Standardabweichung 1.
Dann tun wir so also würden wir kNN auf nur 1 Feature loslassen, dann auf 2, dann auf 3 usw. Man kann zeigen, dass einfach aufgrund der zunehmenden Dimensionalität die Distanzen immer ähnlich werden, d.h. die maximale Distanz rückt dichter and die minimale Distanz. Die ersten 3 Dimensionen können wir ja sogar noch darstellen:
import numpy as np
import matplotlib.pyplot as plt
# Demonstration: Distanzen in verschiedenen Dimensionen
np.random.seed(1)
dimensions = [2, 3, 5, 10, 20, 50, 100]
n_points = 1000
print("Distanzverteilung in verschiedenen Dimensionen:")
ratios = []
for d in dimensions:
# Zufällige Punkte in d Dimensionen (alle gleichmäßig verteilt!)
points = np.random.normal(0, 1, (n_points, d))
# Distanz vom ersten Punkt zu allen anderen
distances = np.sqrt(np.sum((points[1:] - points[0])**2, axis=1))
min_dist = distances.min()
max_dist = distances.max()
mean_dist = distances.mean()
ratio = max_dist / min_dist
ratios.append(ratio)
print(f" {d:3d}D: Min {min_dist:.2f}, Max {max_dist:.2f}, Mittel {mean_dist:.2f} → Verhältnis Max/Min = {ratio:.2f}")Distanzverteilung in verschiedenen Dimensionen:
2D: Min 0.12, Max 5.61, Mittel 2.03 → Verhältnis Max/Min = 45.15
3D: Min 0.22, Max 4.97, Mittel 1.74 → Verhältnis Max/Min = 22.12
5D: Min 0.78, Max 5.91, Mittel 2.94 → Verhältnis Max/Min = 7.56
10D: Min 1.31, Max 6.14, Mittel 3.39 → Verhältnis Max/Min = 4.70
20D: Min 3.71, Max 8.42, Mittel 5.92 → Verhältnis Max/Min = 2.27
50D: Min 7.17, Max 12.91, Mittel 10.08 → Verhältnis Max/Min = 1.80
100D: Min 11.43, Max 16.28, Mittel 13.78 → Verhältnis Max/Min = 1.42Code zeigen/verstecken
import matplotlib.pyplot as plt
# Visualisierung für 1D, 2D und 3D
fig, axes = plt.subplots(1, 3, figsize=(14, 6), layout='tight')
# 1D Visualisierung
ax0 = axes[0]
points_1d = np.random.normal(0, 1, (200, 1))
reference_point_1d = 0 # Referenzpunkt bei 0
distances_1d = np.abs(points_1d[:, 0] - reference_point_1d)
min_idx_1d = np.argmin(distances_1d)
max_idx_1d = np.argmax(distances_1d)
# Alle Punkte auf y=0 plotten
ax0.scatter(points_1d[:, 0], np.zeros(len(points_1d)), alpha=0.6, color='lightblue', s=30)
ax0.scatter(reference_point_1d, 0, color='red', s=100, label='Referenzpunkt (0)')
ax0.scatter(points_1d[min_idx_1d, 0], 0, color='green', s=80,
label=f'Nächster Nachbar (d={distances_1d[min_idx_1d]:.2f})')
ax0.scatter(points_1d[max_idx_1d, 0], 0, color='orange', s=80,
label=f'Fernster Punkt (d={distances_1d[max_idx_1d]:.2f})')
# Linien zu min/max Distanz
ax0.plot([reference_point_1d, points_1d[min_idx_1d, 0]], [0, 0], 'g--', linewidth=4, alpha=0.8)
ax0.plot([reference_point_1d, points_1d[max_idx_1d, 0]], [0, 0], 'orange', linestyle='--', linewidth=4, alpha=0.8)
ax0.set_xlabel('Dimension 1')
ax0.set_ylim(-0.5, 0.5)
ax0.set_title(f'1D: Verhältnis {distances_1d.max()/distances_1d.min():.1f}')
ax0.legend(loc='lower left');
ax0.grid(True, alpha=0.3)
# 2D Visualisierung
ax1 = axes[1]
points_2d = np.random.normal(0, 1, (200, 2))
reference_point_2d = np.array([0, 0]) # Referenzpunkt bei (0,0)
distances_2d = np.sqrt(np.sum((points_2d - reference_point_2d)**2, axis=1))
min_idx_2d = np.argmin(distances_2d)
max_idx_2d = np.argmax(distances_2d)
# Punkte plotten
ax1.scatter(points_2d[:, 0], points_2d[:, 1], alpha=0.6, color='lightblue', s=30)
ax1.scatter(reference_point_2d[0], reference_point_2d[1], color='red', s=100, label='Referenzpunkt (0,0)')
ax1.scatter(points_2d[min_idx_2d, 0], points_2d[min_idx_2d, 1], color='green', s=80,
label=f'Nächster Nachbar (d={distances_2d[min_idx_2d]:.2f})')
ax1.scatter(points_2d[max_idx_2d, 0], points_2d[max_idx_2d, 1], color='orange', s=80,
label=f'Fernster Punkt (d={distances_2d[max_idx_2d]:.2f})')
# Linien zu min/max Distanz
ax1.plot([reference_point_2d[0], points_2d[min_idx_2d, 0]], [reference_point_2d[1], points_2d[min_idx_2d, 1]],
'g--', linewidth=2, alpha=0.8)
ax1.plot([reference_point_2d[0], points_2d[max_idx_2d, 0]], [reference_point_2d[1], points_2d[max_idx_2d, 1]],
'orange', linestyle='--', linewidth=2, alpha=0.8)
ax1.set_xlabel('Dimension 1')
ax1.set_ylabel('Dimension 2')
ax1.set_title(f'2D: Verhältnis {distances_2d.max()/distances_2d.min():.1f}')
ax1.legend(loc='lower left');
ax1.grid(True, alpha=0.3)
# 3D Visualisierung
ax2 = plt.subplot(1, 3, 3, projection='3d')
points_3d = np.random.normal(0, 1, (200, 3))
reference_point_3d = np.array([0, 0, 0]) # Referenzpunkt bei (0,0,0)
distances_3d = np.sqrt(np.sum((points_3d - reference_point_3d)**2, axis=1))
min_idx_3d = np.argmin(distances_3d)
max_idx_3d = np.argmax(distances_3d)
# Punkte plotten
ax2.scatter(points_3d[:, 0], points_3d[:, 1], points_3d[:, 2], alpha=0.6, color='lightblue', s=20)
ax2.scatter(reference_point_3d[0], reference_point_3d[1], reference_point_3d[2], color='red', s=100,
label='Referenzpunkt (0,0,0)')
ax2.scatter(points_3d[min_idx_3d, 0], points_3d[min_idx_3d, 1], points_3d[min_idx_3d, 2], color='green', s=80,
label=f'Nächster Nachbar (d={distances_3d[min_idx_3d]:.2f})')
ax2.scatter(points_3d[max_idx_3d, 0], points_3d[max_idx_3d, 1], points_3d[max_idx_3d, 2], color='orange', s=80,
label=f'Fernster Punkt (d={distances_3d[max_idx_3d]:.2f})')
# Linien zu min/max Distanz
ax2.plot([reference_point_3d[0], points_3d[min_idx_3d, 0]],
[reference_point_3d[1], points_3d[min_idx_3d, 1]],
[reference_point_3d[2], points_3d[min_idx_3d, 2]], 'g--', linewidth=2, alpha=0.8)
ax2.plot([reference_point_3d[0], points_3d[max_idx_3d, 0]],
[reference_point_3d[1], points_3d[max_idx_3d, 1]],
[reference_point_3d[2], points_3d[max_idx_3d, 2]], 'orange', linestyle='--', linewidth=2, alpha=0.8)
ax2.set_xlabel('Dimension 1')
ax2.set_ylabel('Dimension 2')
ax2.set_zlabel('Dimension 3')
ax2.set_title(f'3D: Verhältnis Max/Min = {distances_3d.max()/distances_3d.min():.1f}', pad=10)
ax2.legend(loc='lower left');
plt.show()(-0.5, 0.5)
Die Visualisierungen zeigen das Problem deutlich: Je mehr Dimensionen wir hinzufügen, desto ähnlicher werden sich alle Distanzen - obwohl die Punkte in jeder Dimension identisch verteilt sind!
Dimensionen höher als 3 können wir natürlich nicht mehr visualisieren, aber die Zahlen sprechen für sich: Ab etwa 10-20 Dimensionen sind praktisch alle Punkte “gleich weit” vom Referenzpunkt entfernt. Das Verhältnis zwischen maximaler und minimaler Distanz nähert sich immer mehr der 1 an.
Deshalb funktioniert kNN typischerweise nur gut bei wenigen, sorgfältig ausgewählten Features oder nach Dimensionsreduktion.
In der Praxis wird kNN häufig nach einer Principal Component Analysis (PCA) durchgeführt - einer Dimensionsreduktionsmethode, die wir in einem späteren Kapitel kennenlernen werden.
Die beiden Methoden ergänzen sich perfekt:
- kNN’s Problem: Bei vielen Features (hochdimensionale Daten) funktioniert kNN ggf. nicht mehr so gut.
- PCA’s Lösung: Reduziert die Anzahl der Features auf die wichtigsten Dimensionen und liefert automatisch standardisierte Werte
Das Resultat: Weniger Features, bessere kNN-Performance, und kein manuelles Feature Scaling mehr nötig. Ein Workflow wie PCA → kNN ist daher ein beliebter Klassiker im Machine Learning Toolkit.
Modellvergleich mit Kreuzvalidierung
Zum Abschluss führen wir einen fairen Vergleich zwischen kNN und unseren bisherigen Methoden durch:
# Systematischer Modellvergleich mit Kreuzvalidierung
models = {
'Logistic Regression': LogisticRegression(random_state=42),
'Decision Tree (max_depth=4)': DecisionTreeClassifier(max_depth=4, random_state=42),
'Random Forest (max_depth=4, 100 trees)': RandomForestClassifier(n_estimators=100, max_depth=4, random_state=42),
'K-Nearest Neighbors (k=3)': KNeighborsClassifier(n_neighbors=3),
'K-Nearest Neighbors (k=5)': KNeighborsClassifier(n_neighbors=5)
}
# Kreuzvalidierung Setup (wie in vorherigen Kapiteln)
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=10, random_state=42)
cv_results = {}
for name, model in models.items():
scores = cross_val_score(model, X_train_scaled, y_train, cv=cv, scoring='accuracy')
cv_results[name] = {
'scores': scores,
'mean': scores.mean(),
'std': scores.std()
}
# Ergebnisse zusammenfassen
results_summary = []
for name in models.keys():
results_summary.append({
'Methode': name,
'CV Accuracy (Mittel)': cv_results[name]['mean'],
'CV Accuracy (Std)': cv_results[name]['std']
})
results_df = pd.DataFrame(results_summary)
results_df = results_df.sort_values('CV Accuracy (Mittel)', ascending=False)
print("\nKreuzvalidierungs-Ergebnisse (50 Folds: 5×10 Wiederholungen):")
print(results_df.to_string(index=False, float_format='%.4f'))
# Beste Methode identifizieren
best_method = results_df.iloc[0]['Methode']
best_score = results_df.iloc[0]['CV Accuracy (Mittel)']
print(f"\nBeste Methode: {best_method} mit {best_score:.4f} Accuracy")
Kreuzvalidierungs-Ergebnisse (50 Folds: 5×10 Wiederholungen):
Methode CV Accuracy (Mittel) CV Accuracy (Std)
Random Forest (max_depth=4, 100 trees) 0.9824 0.0176
K-Nearest Neighbors (k=5) 0.9810 0.0191
K-Nearest Neighbors (k=3) 0.9805 0.0189
Logistic Regression 0.9771 0.0198
Decision Tree (max_depth=4) 0.9698 0.0199
Beste Methode: Random Forest (max_depth=4, 100 trees) mit 0.9824 AccuracyVor- und Nachteile von K-Nearest Neighbors
Vorteile:
- Einfach zu verstehen: Das Konzept ist sehr intuitiv
- Keine Annahmen über Datenverteilung: Non-parametrische Methode
- Flexibel: Kann komplexe, nichtlineare Entscheidungsgrenzen lernen
- Funktioniert für Klassifikation und Regression: Vielseitig einsetzbar
- Kein Training nötig: Neue Daten können sofort verwendet werden
Nachteile:
- Rechenaufwändig bei Vorhersagen: Jede Vorhersage erfordert Distanzberechnung zu allen Trainingspunkten
- Speicher-intensiv: Alle Trainingsdaten müssen gespeichert werden
- Empfindlich für irrelevante Features: Curse of Dimensionality
- Benötigt Feature Scaling: Ohne Skalierung dominieren Features mit großen Wertebereichen
- Schwierig bei unbalancierten Datensätzen: Minderheitsklassen werden oft überstimmt
Zusammenfassung
K-Nearest Neighbors zeigt uns einen völlig anderen Ansatz für maschinelles Lernen:
- Instance-based Learning: Entscheidungen basieren auf der Ähnlichkeit zu bekannten Beispielen
-
Lazy Learning: Keine aufwändige Trainingsphase, aber rechenintensive Vorhersagen
- Feature Scaling ist kritisch: Erste Methode in unserem Kurs, die zwingend Skalierung benötigt
- Intuitive Interpretation: Die “Nachbarschafts”-Logik ist leicht nachvollziehbar
- Flexibel aber teuer: Kann komplexe Muster lernen, aber mit hohen Rechenkosten
kNN erweitert unser Klassifikations-Werkzeugkasten um eine wichtige Kategorie von Algorithmen. In vielen praktischen Anwendungen - besonders bei kleineren Datensätzen oder als Baseline-Modell - ist kNN eine wertvolle Option.
- K-nächste Nachbarn (KNN) in 3 Minuten - am besten die Tonspur auf Englisch stellen, falls ihr die KI-generierte deutsche vorgesetzt bekommt.
Übungen
Übung: kNN Performance und der Einfluss von Feature Scaling
Verwende den Palmer Penguins Datensatz für eine Adelie vs. Chinstrap Klassifikation mit drei numerischen Features: bill_length_mm, bill_depth_mm und body_mass_g. Diese Kombination zeigt besonders deutlich, warum Feature Scaling bei kNN kritisch ist.
Datenvorbereitung (vorgegeben):
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split, RepeatedStratifiedKFold, cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
np.random.seed(42)
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Nur Adelie und Chinstrap auswählen
penguins_binary = penguins[penguins['species'].isin(['Adelie', 'Chinstrap'])].copy()
# Drei spezielle Features verwenden (zeigen starken Scaling-Effekt)
features = ['bill_length_mm', 'bill_depth_mm', 'body_mass_g']
penguins_clean = penguins_binary.dropna(subset=features + ['species'])
# Features und Ziel definieren
X = penguins_clean[features]
y = (penguins_clean['species'] == 'Chinstrap').astype(int) # 0=Adelie, 1=Chinstrap
print(f"Datensatz: {len(X)} Pinguine mit {len(features)} Features")
print(f"Klassen: Adelie (0): {sum(y==0)}, Chinstrap (1): {sum(y==1)}")Teil 1: Einfluss von Feature Scaling
- Erstelle einen 75/25 Train-Test Split (mit
stratify=y) - Trainiere zwei kNN-Modelle mit k=5:
- Modell A: Ohne Standardisierung der Features
-
Modell B: Mit Standardisierung der Features (verwende
StandardScaler)
- Berechne für beide Modelle die Test Accuracy
- Analysiere die Wertebereiche der Features und erkläre, warum Feature Scaling einen so großen Unterschied macht
Teil 2: Optimales k finden
- Verwende die standardisierten Features und teste verschiedene k-Werte:
[1, 3, 5, 7, 9, 20, 30, 40, 50] - Verwende Repeated Stratified K-Fold Cross Validation (5 Folds, 3 Wiederholungen) für jedes k
- Berechne für jedes k sowohl Training als auch Test Accuracy über die Cross Validation
- Erstelle eine Grafik die Training und Test Accuracy über die verschiedenen k-Werte zeigt
- Identifiziere das optimale k basierend auf der besten Test Performance