import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.stats.multicomp import pairwise_tukeyhsd
import itertools
np.random.seed(42) # für reproduzierbare ErgebnisseZweifaktorielle ANOVA und Interaktionseffekte
Im vorangegangenen Kapitel haben wir die einfaktorielle ANOVA kennengelernt, mit der wir die Mittelwerte mehrerer Gruppen bezüglich eines einzigen Faktors vergleichen konnten. In der Praxis gibt es jedoch auch Situationen, in denen wir den Einfluss mehrerer Faktoren gleichzeitig untersuchen möchten. Hier kommt die zweifaktorielle ANOVA (bzw. mehrfaktorielle ANOVA) ins Spiel, die es uns ermöglicht, den Effekt von mehrerene Faktoren und - noch wichtiger - deren Interaktion(en) zu analysieren.
Der Grund, warum wir erst jetzt zum ersten Mal über Wechselwirkungen/Interaktionen sprechen, liegt daran, dass wir bisher meist nur einen Term im Modell hatten: bei der linearen Regression einen Prädiktor, bei der Polynomregression Potenzen derselben Variable, oder bei der einfaktoriellen ANOVA einen Faktor. Gibt es nur einen Term, kann dieser mit nichts interagieren.
Eine Ausnahme war das Kapitel zur multiplen linearen Regression - dort hätten die verschiedenen Prädiktoren tatsächlich miteinander interagieren können. Aus didaktischen Gründen haben wir das aber erstmal ignoriert und nur additive Effekte betrachtet.
Nun erweitern wir unser Verständnis und betrachten Modelle mit mehreren Faktoren, die miteinander in Wechselwirkung stehen können.
Bevor wir in die praktische Anwendung einsteigen, müssen wir einige wichtige Begriffe klären bzw. wiederholen:
Faktor (auch: Faktoreffekt, engl. factor, treatment): Ein Faktor ist eine kategorielle Variable, deren Einfluss auf die Zielvariable untersucht wird. Ein Modell mit einem Faktor (z.B. Pinguinart) haben wir schon in der einfaktoriellen ANOVA gesehen haben.
Stufen oder Level (engl. levels, factor levels): Die verschiedenen Ausprägungen eines Faktors nennt man Stufen/Level. Der Faktor “Pinguinart” hatte die drei Stufen “Adelie”, “Chinstrap” und “Gentoo”. Ein Faktor “Behandlung” könnte beispielsweise die zwei Stufen “Normaldosis” und “Placebo” haben.
Haupteffekte (engl. main effects): Der Haupteffekt bezeichnet den durchschnittlichen Effekt eines Faktors über alle Stufen der (ggf. vorhandenen) anderen Faktoren hinweg. In der einfaktoriellen ANOVA hatten wir ein Modell mit einem Haupteffekt.
Interaktionseffekte oder Wechselwirkungseffekte (engl. interaction effects, interaction terms): Eine Interaktion zwischen zwei Faktoren liegt vor, wenn die Wirkung der Faktoren nicht einfach additiv ist, also nicht durch die Summe der beiden Haupteffekte erklärt werden kann. Mit anderen Worten: Eine Interaktion liegt vor, wenn die Wirkung eines Faktors davon abhängt, welche Ausprägung ein anderer Faktor hat. Die Effekte sind dann nicht mehr einfach additiv. Interaktionseffekte erlauben also (zusätzliche) Effekte für alle Faktorstufenkombinationen.
Ein landwirtschaftliches Experiment
Um das Konzept der Interaktionen zu verstehen, betrachten wir ein landwirtschaftliches Experiment. Ein Forschungsteam möchte herausfinden, welche Kombination aus Dünger und Pflanzensorte den höchsten Ertrag bringt. Sie testen dafür zwei verschiedene Dünger und 4 verschiedene Sorten. Die Faktoren und Stufen sind:
- Dünger (Faktor 1): 2 Stufen (Toad, Yoshi)
- Sorte (Faktor 2): 4 Stufen (Simba, Nala, Timon, Pumba)
Demnach gibt es 8 Kombinationen. Alle Kombinationen wurden in 3 Wiederholungen getestet, sodass wir 2*4*3 = 24 Beobachtungen haben:
# Experimentdaten laden
original_data = {
'duenger': ['Toad', 'Toad', 'Toad', 'Toad', 'Yoshi', 'Yoshi', 'Yoshi', 'Yoshi',
'Toad', 'Toad', 'Toad', 'Toad', 'Yoshi', 'Yoshi', 'Yoshi', 'Yoshi',
'Toad', 'Toad', 'Toad', 'Toad', 'Yoshi', 'Yoshi', 'Yoshi', 'Yoshi'],
'sorte': ['Simba', 'Nala', 'Timon', 'Pumba'] * 6,
'ertrag': [6192, 6269, 5522, 4504, 7470, 7862, 7260, 1594,
7146, 6872, 5970, 5126, 7578, 6324, 6392, 1690,
6860, 6444, 6550, 4218, 7642, 6666, 6410, 2856]
}
df = pd.DataFrame(original_data)
df duenger sorte ertrag
0 Toad Simba 6192
1 Toad Nala 6269
2 Toad Timon 5522
3 Toad Pumba 4504
4 Yoshi Simba 7470
5 Yoshi Nala 7862
6 Yoshi Timon 7260
7 Yoshi Pumba 1594
8 Toad Simba 7146
9 Toad Nala 6872
10 Toad Timon 5970
11 Toad Pumba 5126
12 Yoshi Simba 7578
13 Yoshi Nala 6324
14 Yoshi Timon 6392
15 Yoshi Pumba 1690
16 Toad Simba 6860
17 Toad Nala 6444
18 Toad Timon 6550
19 Toad Pumba 4218
20 Yoshi Simba 7642
21 Yoshi Nala 6666
22 Yoshi Timon 6410
23 Yoshi Pumba 2856Erste Datenexploration
Um ein Gefühl für die Daten zu bekommen können wir wie so oft z.B. einfache Mittelwerte und Standardabweichungen berechnen. Allerdings haben wir nun mehrere Optionen wofür wir das tun, also wonach wir gruppieren. Jeweils pro Faktor (Haupteffekte)…
(
df.groupby(['duenger'])['ertrag']
.agg(mean=lambda x: round(x.mean(), 1), sd=lambda x: round(x.std(), 1), n='count')
.reset_index()
.sort_values('mean', ascending=False)
) duenger mean sd n
0 Toad 5972.8 944.8 12
1 Yoshi 5812.0 2349.5 12(
df.groupby(['sorte'])['ertrag']
.agg(mean=lambda x: round(x.mean(), 1), sd=lambda x: round(x.std(), 1), n='count')
.reset_index()
.sort_values('mean', ascending=False)
) sorte mean sd n
2 Simba 7148.0 553.1 6
0 Nala 6739.5 594.0 6
3 Timon 6350.7 583.7 6
1 Pumba 3331.3 1504.7 6…oder eben für deren Kombinationen (Interaktionseffekte):
(
df.groupby(['duenger', 'sorte'])['ertrag']
.agg(mean=lambda x: round(x.mean(), 1), sd=lambda x: round(x.std(), 1), n='count')
.reset_index()
.sort_values('mean', ascending=False)
) duenger sorte mean sd n
6 Yoshi Simba 7563.3 86.9 3
4 Yoshi Nala 6950.7 807.6 3
2 Toad Simba 6732.7 489.6 3
7 Yoshi Timon 6687.3 496.0 3
0 Toad Nala 6528.3 310.2 3
3 Toad Timon 6014.0 515.4 3
1 Toad Pumba 4616.0 464.2 3
5 Yoshi Pumba 2046.7 702.5 3Hier verwenden wir zum ersten Mal Lambda-Funktionen - kleine, anonyme Funktionen für einfache Operationen. Mehr Details zu Lambda-Funktionen findest du im Kapitel “Verschiedenes”.
Diese Zahlen geben uns bereits erste Hinweise: Im Durchschnitt scheinen Dünger Toad, und Sorte Simba die beste Wahl zu sein. Gleichzeitig ist die Kombination aus Toad-Simba nur die drittbeste von allen 8. Das kann bereits als Hinweis für eine mögliche Interaktion zwischen den Faktoren Dünger und Sorte gewertet werden. Schauen wir uns das mit einer Visualisierung genauer an.
Visualisierung der Daten
Code zeigen/verstecken
def plot_two_way_data(data, factor1_col, factor2_col, outcome_col,
factor1_name, factor2_name, outcome_name,
factor1_colors=['#FF6B6B', '#4ECDC4'], title=None,
ax=None, show_legend=True, ylim=None):
"""
Erstellt einen Scatterplot für zweifaktorielle Daten mit Jitter und Gruppenmittelwerten.
"""
# Gruppenmittelwerte berechnen
group_means = data.groupby([factor2_col, factor1_col])[outcome_col].mean().reset_index()
# Farben zuweisen
factor2_levels = sorted(data[factor2_col].unique())
colors = {factor2_levels[0]: factor1_colors[0], factor2_levels[1]: factor1_colors[1]}
# Figure/Axis handling
if ax is None:
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
show_plot = True
else:
show_plot = False
# x-Positionen für factor1 Stufen
factor1_levels = sorted(data[factor1_col].unique())
x_positions = {level: i for i, level in enumerate(factor1_levels)}
# Scatterplot mit Jitter
np.random.seed(42) # für reproduzierbare Jitter-Werte
for factor2_level in factor2_levels:
factor2_data = data[data[factor2_col] == factor2_level]
for factor1_level in factor1_levels:
level_data = factor2_data[factor2_data[factor1_col] == factor1_level][outcome_col]
# Jitter hinzufügen um Überlappungen zu vermeiden
if factor2_level == factor2_levels[0]:
x_jitter = np.random.normal(x_positions[factor1_level] - 0.15, 0.05, len(level_data))
else:
x_jitter = np.random.normal(x_positions[factor1_level] + 0.15, 0.05, len(level_data))
ax.scatter(x_jitter, level_data,
color=colors[factor2_level], alpha=0.7, s=60,
label=f'{factor2_name} {factor2_level}' if factor1_level == factor1_levels[0] else '')
# Gruppenmittelwerte als horizontale Linien hinzufügen
for factor1_level in factor1_levels:
for factor2_level in factor2_levels:
mean_value = group_means[(group_means[factor2_col] == factor2_level) &
(group_means[factor1_col] == factor1_level)][outcome_col].iloc[0]
if factor2_level == factor2_levels[0]:
ax.hlines(y=mean_value, xmin=x_positions[factor1_level] - 0.25,
xmax=x_positions[factor1_level] - 0.05,
colors=colors[factor2_level], linestyles='--', linewidth=2)
else:
ax.hlines(y=mean_value, xmin=x_positions[factor1_level] + 0.05,
xmax=x_positions[factor1_level] + 0.25,
colors=colors[factor2_level], linestyles='--', linewidth=2)
ax.set_xlabel(factor1_name)
ax.set_ylabel(outcome_name)
ax.set_title(title if title else f'{outcome_name} nach {factor2_name} und {factor1_name}')
ax.set_xticks(list(x_positions.values()))
ax.set_xticklabels(factor1_levels)
if ylim is not None:
ax.set_ylim(ylim)
if show_legend:
ax.legend()
ax.grid(True, alpha=0.3)
if show_plot:
plt.show()# Farben für die echten Daten definieren
real_data_colors = ['#e91c04', '#74bb35']
# Plot für echte Daten erstellen
plot_two_way_data(df, 'sorte', 'duenger', 'ertrag',
'Pflanzensorte', 'Dünger', 'Ertrag (kg/ha)',
factor1_colors=real_data_colors,
title='Ertrag nach Dünger und Sorte')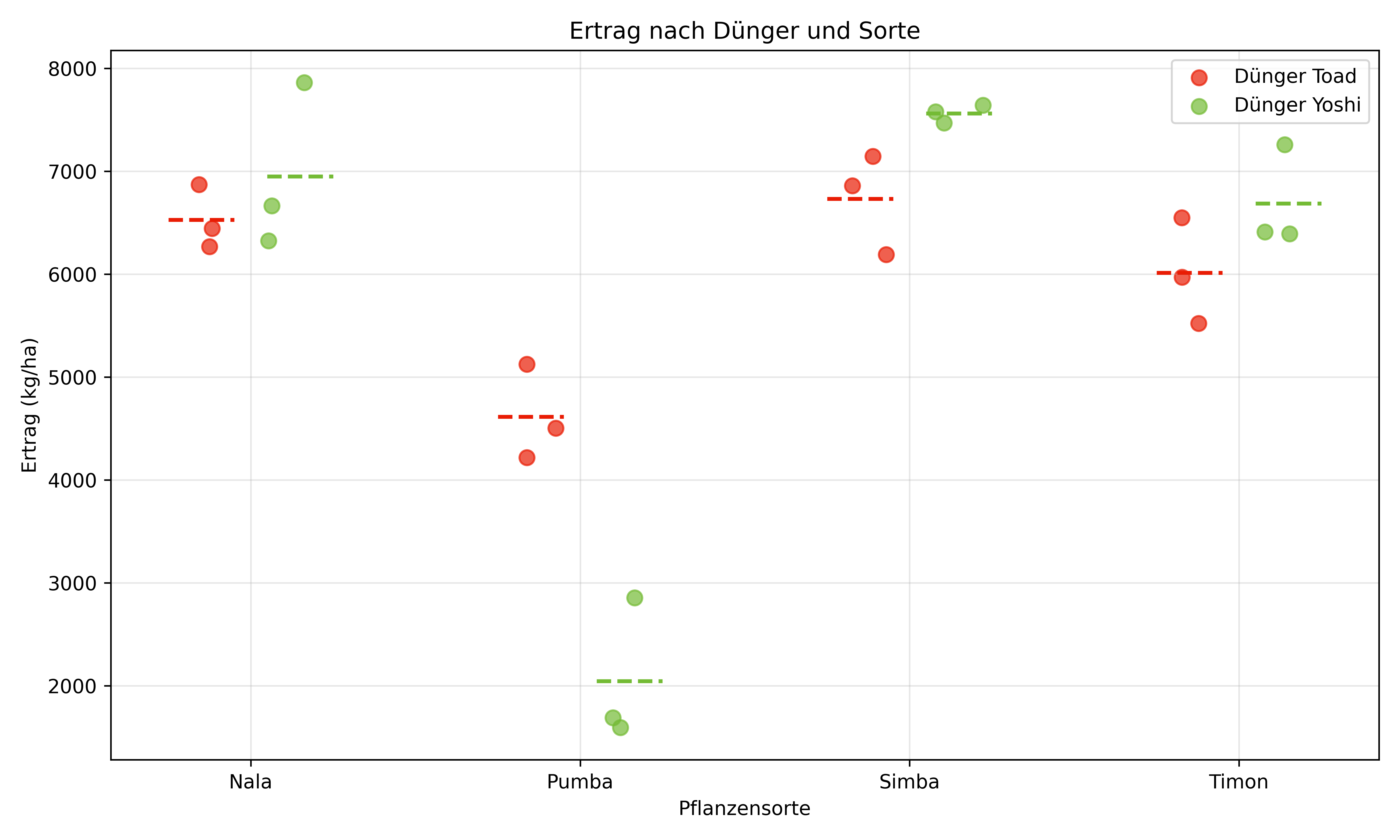
Diese Visualisierung zeigt ein auffälliges Muster: Erstmal fällt auf, dass die Sorten Nala, Simba und Timon alle generell höhere Erträge liefern als Pumba. Auch gilt für diese drei Sorten, dass Dünger Yoshi tendenziell bessere Erträge liefert als Toad.
Bei Sorte Pumba ist es jedoch genau umgekehrt: Hier liefert Toad deutlich bessere Erträge als Yoshi.
Das ist ein klares Anzeichen für eine Interaktion zwischen den beiden Faktoren. Der Effekt des Düngers hängt von der gewählten Sorte ab.
Die fünf Grundszenarien verstehen
Um das Konzept der Interaktionen besser zu verstehen, simulieren wir verschiedene Szenarien mit einem vereinfachten 2×2-Design (2 Sorten, 2 Dünger). Dies hilft uns, die verschiedenen Möglichkeiten zu verstehen, wie Faktoren miteinander wirken können:
Code zeigen/verstecken
def create_scenario_data(scenario_type):
"""Erstelle Daten für verschiedene ANOVA-Szenarien mit exakten Mittelwerten"""
np.random.seed(42)
# Basis-Setup: 2 Faktoren mit je 2 Stufen, 8 Wiederholungen pro Kombination
n_per_group = 10
# Definiere Mittelwerte für verschiedene Szenarien
if scenario_type == "nur_intercept":
means = {'A_X': 100, 'A_Y': 100, 'B_X': 100, 'B_Y': 100}
elif scenario_type == "nur_faktor1":
means = {'A_X': 120, 'A_Y': 120, 'B_X': 80, 'B_Y': 80}
elif scenario_type == "nur_faktor2":
means = {'A_X': 80, 'A_Y': 120, 'B_X': 80, 'B_Y': 120}
elif scenario_type == "beide_haupteffekte":
means = {'A_X': 90, 'A_Y': 130, 'B_X': 70, 'B_Y': 110}
elif scenario_type == "mit_interaktion":
means = {'A_X': 90, 'A_Y': 130, 'B_X': 110, 'B_Y': 70}
# Daten generieren mit exakten Mittelwerten
data = []
for sorte in ['A', 'B']:
for duenger in ['X', 'Y']:
key = f"{sorte}_{duenger}"
target_mean = means[key]
# Erzeuge exakt n_per_group Werte mit dem gewünschten Mittelwert
# Methode: Erzeuge symmetrische Abweichungen um den Mittelwert
deviations = np.random.normal(0, 8, n_per_group)
# Zentriere die Abweichungen so, dass ihr Mittelwert exakt 0 ist
deviations = deviations - np.mean(deviations)
# Addiere den gewünschten Mittelwert
values = target_mean + deviations
for value in values:
data.append({'sorte': sorte, 'duenger': duenger, 'ertrag': value})
return pd.DataFrame(data)
# Alle fünf Szenarien erstellen
scenarios = {
"Nur Intercept": create_scenario_data("nur_intercept"),
"Nur Sorte-Effekt": create_scenario_data("nur_faktor1"),
"Nur Dünger-Effekt": create_scenario_data("nur_faktor2"),
"Beide Haupteffekte": create_scenario_data("beide_haupteffekte"),
"Mit Interaktion": create_scenario_data("mit_interaktion")
}
# Farben für die Szenarien
scenario_colors = ['#2a9d8f', '#e76f51']
# Visualisierung der fünf Szenarien
fig, axes = plt.subplots(2, 3, figsize=(12, 8), layout='tight')
axes = axes.flatten()
for idx, (title, data) in enumerate(scenarios.items()):
if idx >= 5: # Nur 5 Szenarien
axes[idx].set_visible(False)
continue
# Funktion für jedes Szenario verwenden mit dem entsprechenden Axis
plot_two_way_data(data, 'sorte', 'duenger', 'ertrag',
'Sorte', 'Dünger', 'Ertrag',
factor1_colors=scenario_colors,
title=title,
ax=axes[idx],
show_legend=False,
ylim=(50, 150))
# Letzten Plot ausblenden
# Legende im letzten Panel hinzufügen
axes[5].set_visible(True)
axes[5].axis('off') # Achsen ausblenden
# Manuelle Legende erstellen
from matplotlib.patches import Patch
legend_elements = [Patch(facecolor=scenario_colors[0], label='Dünger X'),
Patch(facecolor=scenario_colors[1], label='Dünger Y')]
axes[5].legend(handles=legend_elements, loc='center', fontsize=12, frameon=False)
plt.show()(np.float64(0.0), np.float64(1.0), np.float64(0.0), np.float64(1.0))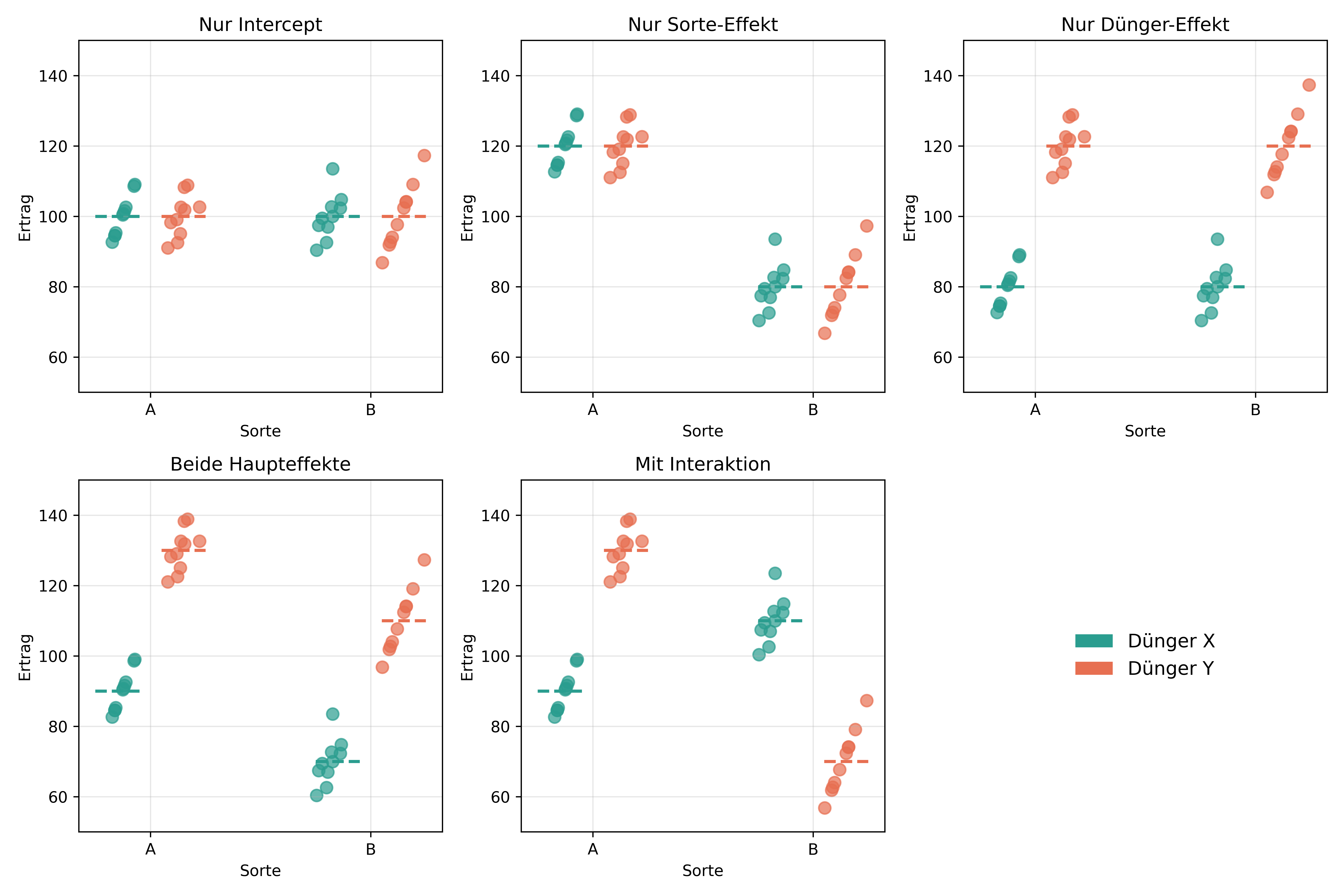
Diese fünf Szenarien veranschaulichen die verschiedenen Möglichkeiten:
- Nur Intercept: Kein Faktor hat einen Effekt - alle Mittelwerte sind gleich
- Nur Sorte-Effekt: Sorte A erzielt höhere Erträge als B, unabhängig vom Dünger
- Nur Dünger-Effekt: Dünger Y führt zu höheren Erträgen, unabhängig von der Sorte
- Beide Haupteffekte: Sowohl Sorte als auch Dünger haben additive Effekte
- Mit Interaktion: Die Dünger-Wirkung hängt von der Sorte ab
Der entscheidende Unterschied zwischen Szenario 4 und 5 ist, dass bei einer Interaktion die Effekte nicht einfach addiert werden können. In Szenario 5 ist Dünger Y besser für Sorte A, aber Dünger X besser für Sorte B.
Das mathematische Modell
Das vollständige Modell für die zweifaktorielle ANOVA mit Interaktion lautet:
\[\text{Ertrag}_{ijk} = \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij} + \varepsilon_{ijk}\]
Dabei ist:
- \(\mu\) der Gesamtmittelwert (Intercept)
- \(\alpha_i\) der Haupteffekt des Düngerfaktors (Stufe i)
-
\(\beta_j\) der Haupteffekt des Sortenfaktors (Stufe j)
- \((\alpha\beta)_{ij}\) der Interaktionseffekt zwischen Dünger und Sorte
- \(\varepsilon_{ijk}\) der Fehlerterm für Beobachtung k in Kombination ij
Anders ausgedrückt: Zusätzlich zu den beiden Haupteffekten haben wir nun Interaktionsterme, die beschreiben, wie sich die Faktoren gegenseitig beeinflussen. In gewisser Hinsicht beschreibt jeder Interaktionsterm die Abweichung von dem, was man bei additiven Effekten erwarten würde.
Matrix-Darstellung des Modells
Wie schon im Kapitel zur Matrix-Notation können wir dieses Modell auch in Matrix-Form darstellen. Dabei wird deutlich, wie schnell die Design-Matrix anwächst, wenn wir Interaktionsterme hinzufügen. Betrachten wir die ersten sechs Beobachtungen unseres Datensatzes:
\[\begin{bmatrix} \text{Ertrag}_1 \\ \text{Ertrag}_2 \\ \text{Ertrag}_3 \\ \text{Ertrag}_4 \\ \text{Ertrag}_5 \\ \text{Ertrag}_6 \\ \vdots \\ \text{Ertrag}_{24} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & 1 & 1 & 0 & 0 & 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} \beta_0 \\ \beta_{\text{Yoshi}} \\ \beta_{\text{Pumba}} \\ \beta_{\text{Simba}} \\ \beta_{\text{Timon}} \\ \beta_{\text{Yoshi:Pumba}} \\ \beta_{\text{Yoshi:Simba}} \\ \beta_{\text{Yoshi:Timon}} \end{bmatrix} + \begin{bmatrix} \varepsilon_1 \\ \varepsilon_2 \\ \varepsilon_3 \\ \varepsilon_4 \\ \varepsilon_5 \\ \varepsilon_6 \\ \vdots \\ \varepsilon_{24} \end{bmatrix}\]
Die ersten sechs Beobachtungen sind:
- Toad + Simba (Zeile 1: Referenz-Dünger + Simba)
- Toad + Nala (Zeile 2: Referenz-Dünger + Referenz-Sorte → alle Koeffizienten = 0)
- Toad + Timon (Zeile 3: Referenz-Dünger + Timon)
- Toad + Pumba (Zeile 4: Referenz-Dünger + Pumba)
- Yoshi + Simba (Zeile 5: Yoshi + Simba + deren Interaktion)
- Yoshi + Nala (Zeile 6: Yoshi + Referenz-Sorte)
Hier wird deutlich sichtbar:
- Die Design-Matrix \(\mathbf{X}\) hat 24 Zeilen (eine pro Beobachtung) und 8 Spalten (eine pro Parameter)
- Der Parameter-Vektor \(\mathbf{\beta}\) hat entsprechend 8 Elemente
- Referenzkategorien: Toad (Dünger) und Nala (Sorte) werden nicht explizit geschätzt
- Interaktionsreferenz: Alle Interaktionseffekte, die mindestens eine Referenzkategorie enthalten, werden automatisch auf 0 gesetzt nicht geschätzt
Bei 2 Dünger & 4 Sorten ergeben sich:
- 1 Intercept
- 1 Haupteffekt für Dünger (Yoshi [vs. Toad])
- 3 Haupteffekte für Sorte (Pumba, Simba, Timon [jeweils vs. Nala])
- 3 Interaktionseffekte (Yoshi×Pumba, Yoshi×Simba, Yoshi×Timon)
Insgesamt also 8 Parameter zu schätzen. Bei größeren Designs wächst diese Zahl sehr schnell an!
Implementierung der zweifaktoriellen ANOVA
Nun haben wir verstanden was Interaktionen sind und wie sie sich auf unsere Daten auswirken können. Die Betonung liegt aber auf können, da wir ja vor der Auswertung nicht wissen ob unsere Faktoren tatsächlich interagieren. Ob sie es tun könnte der Hauptfokus der gesamten Studie sein. Daher müssen wollen wir also die Interaktion prüfen bzw. statistisch testen. Das geht mit einer zweifaktoriellen ANOVA.
Wie wir die Haupteffekte ins Modell aufnehmen, haben wir bereits in der einfaktoriellen ANOVA gesehen. Wir würden also hier die Formel ertrag ~ C(duenger) + C(sorte) verwenden. Um zusätzlich noch einen Interaktionsterm hinzuzufügen, kann man einen Doppelpunkt verwenden: C(duenger):C(sorte), sodass das volle Modell wäre: ertrag ~ C(duenger) + C(sorte) + C(duenger):C(sorte)
Wir können das aber auch kürzer schreiben als C(duenger) * C(sorte). Das Sternchen bedeutet, dass wir sowohl alle Haupteffekte als auch Interaktionseffekte einbeziehen wollen. Das mag in diesem Fall noch nicht allzu nützlich erscheinen, aber wenn man sich klar macht, dass es ja auch mehr als zwei Faktoren geben kann, wird es schnell unübersichtlich. Daher ist die Kurzschreibweise sehr praktisch.
-
A*BentsprichtA + B + A:B -
A*B*CentsprichtA + B + C + A:B + A:C + B:C + A:B:C -
A*B*C*DentsprichtA + B + C + D + A:B + A:C + A:D + B:C + B:D + C:D + A:B:C + A:B:D + A:C:D + B:C:D + A:B:C:D - usw.
mod_voll = smf.ols('ertrag ~ C(duenger) + C(sorte) + C(duenger):C(sorte)', data=df).fit()
sm.stats.anova_lm(mod_voll, typ=3) sum_sq df F PR(>F)
Intercept 1.278574e+08 1.0 461.495164 3.168652e-13
C(duenger) 2.675482e+05 1.0 0.965702 3.403818e-01
C(sorte) 8.185855e+06 3.0 9.848817 6.418724e-04
C(duenger):C(sorte) 1.172979e+07 3.0 14.112708 9.292665e-05
Residual 4.432806e+06 16.0 NaN NaNDie ANOVA-Tabelle zeigt uns drei wichtige F-Tests:
- Haupteffekt Dünger: Unterscheiden sich die Düngerarten im Durchschnitt?
- Haupteffekt Sorte: Unterscheiden sich die Sorten im Durchschnitt?
- Interaktionseffekt: Hängt die Wirkung des Düngers von der Sorte ab?
Das Wichtigste: Die Ergebnisse zeigen eine signifikante Interaktion (p < 0.001), was bestätigt, was wir bereits in der Visualisierung gesehen haben: Es gibt mindestens eine Kombination von Dünger und Sorte, bei der die Effekte nicht additiv sind (weil sich deren Wechselwirkungseffekt von den anderen unterscheidet).
Wie bei der einfaktoriellen ANOVA gelten auch hier die üblichen Modellannahmen (Normalverteilung der Residuen, Varianzhomogenität, Unabhängigkeit).
Interaktionsplots zur Veranschaulichung
Ein Interaktionsplot ist eine sehr gute Methode, um Wechselwirkungen zu visualisieren. Er zeigt die Mittelwerte der Kombinationen und verbindet sie mit Linien:
# Interaktionsplot erstellen
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
# Daten für den Plot vorbereiten
sorten = ['Simba', 'Nala', 'Timon', 'Pumba']
duenger_arten = ['Toad', 'Yoshi']
# Mittelwerte für jede Kombination berechnen
for duenger in duenger_arten:
means = []
for sorte in sorten:
mean_val = df[(df['duenger'] == duenger) & (df['sorte'] == sorte)]['ertrag'].mean()
means.append(mean_val)
ax.plot(range(len(sorten)), means, marker='o', linewidth=2, markersize=8,
label=f'Dünger {duenger}', color=real_data_colors[duenger_arten.index(duenger)])
ax.set_xlabel('Pflanzensorte')
ax.set_ylabel('Mittlerer Ertrag (kg/ha)')
ax.set_title('Interaktionsplot: Dünger × Sorte')
ax.set_xticks(range(len(sorten)))
ax.set_xticklabels(sorten)
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()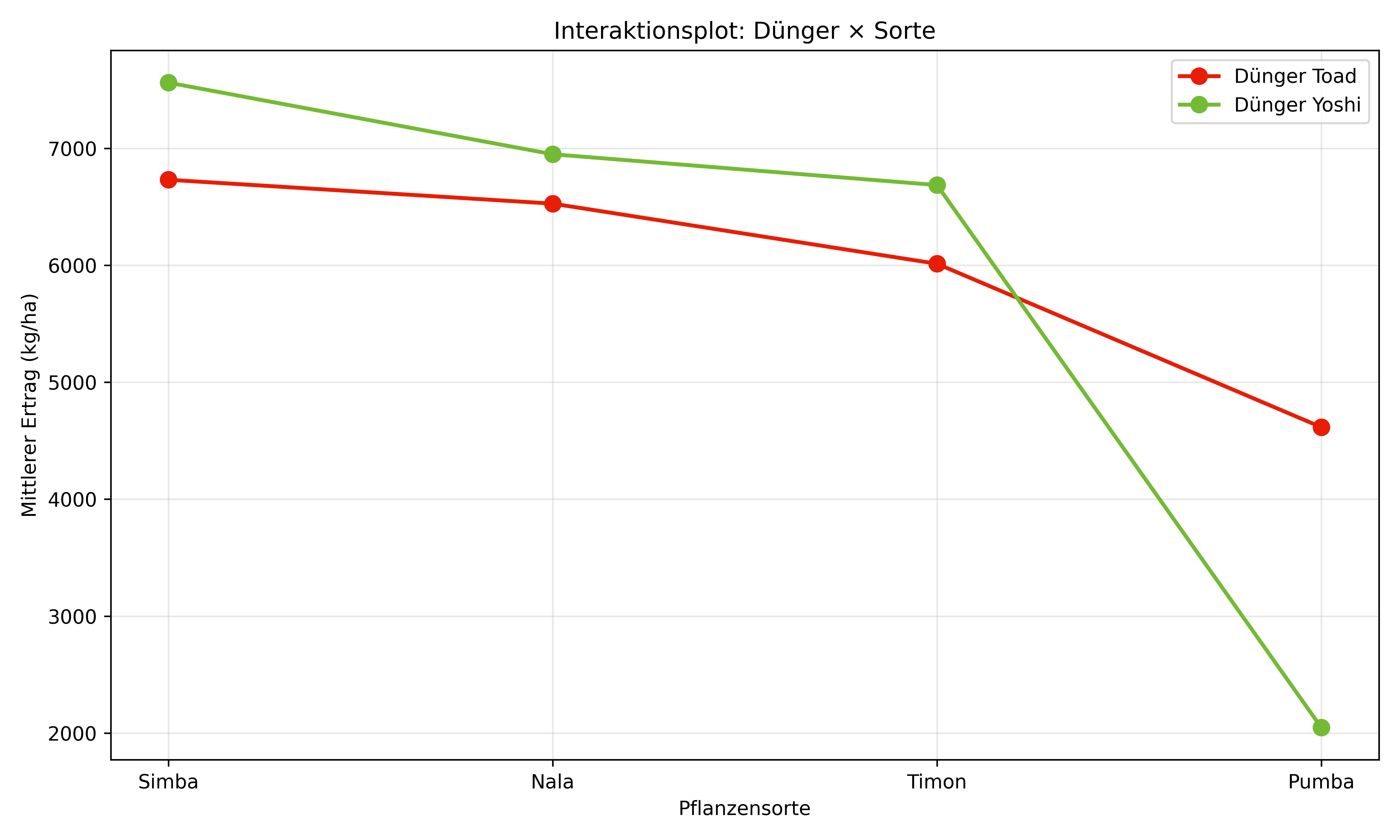
Interpretation des Interaktionsplots:
- Parallele Linien: Keine Interaktion - die Dünger-Effekte sind für alle Sorten gleich
- Sich kreuzende oder divergierende Linien: Sich kreuzende oder deutlich divergierende Linien deuten auf eine Interaktion hin. Ob diese statistisch signifikant ist, muss jedoch durch die ANOVA getestet werden.
In unserem Plot sehen wir deutlich, dass die Linien nicht parallel verlaufen und sich sogar bei Sorte Pumba kreuzen. Dies bestätigt die signifikante Interaktion aus unserer ANOVA.
Post-hoc-Tests bei signifikanter Interaktion
Da unsere ANOVA eine signifikante Interaktion zeigt, ist es nicht sinnvoll, die Haupteffekte isoliert zu interpretieren. Stattdessen sollten wir alle Kombinationen miteinander vergleichen. Um das klarer zu machen sollten wir nochmal zurück zur ursprünglichen Fragestellung: Ein Landwirt möchte wissen, welchen Dünger er kaufen soll.
In einem Szenario ohne Interaktionen könnte man relativ einfach antworten: “Nimm Dünger Y, der führt zu höheren Erträgen.” und “Nimm Sorte A, die hat den höchsten Ertrag.”
In unserem Fall mit signifikanter Interaktion gibt es keine einfachen Antworten. Stattdessen müssen wir differenzieren.
Das ist die Kernbotschaft bei Interaktionseffekten: Der Effekt eines Faktors hängt von der Ausprägung des anderen Faktors ab. Dies macht die Interpretation komplexer, aber auch realitätsnäher, da viele biologische, technische und soziale Prozesse tatsächlich solche Wechselwirkungen aufweisen.
Konkret auf den post-hoc-Test (z.B. wieder Tukey) bezogen bedeutet das, dass wir alle Kombinationen von Dünger und Sorte vergleichen müssen, um herauszufinden, welche sich signifikant voneinander unterscheiden. Wir vergleichen also nicht die zwei Dünger miteinander (= 1 Test) und nicht die vier Sorten miteinander (= 6 Tests), sondern müssen die 8 Kombinationen miteinander vergleichen (= 28 Tests).
# Neue Variable für Kombination erstellen
df['kombination'] = df['duenger'] + '_' + df['sorte']
print("Verfügbare Kombinationen:")
print(sorted(df['kombination'].unique()))
# Tukey-Test für alle paarweisen Vergleiche der Kombinationen
tukey_results = pairwise_tukeyhsd(
endog=df['ertrag'],
groups=df['kombination'],
alpha=0.05
)
print(tukey_results)Verfügbare Kombinationen:
['Toad_Nala', 'Toad_Pumba', 'Toad_Simba', 'Toad_Timon', 'Yoshi_Nala', 'Yoshi_Pumba', 'Yoshi_Simba', 'Yoshi_Timon']
Multiple Comparison of Means - Tukey HSD, FWER=0.05
======================================================================
group1 group2 meandiff p-adj lower upper reject
----------------------------------------------------------------------
Toad_Nala Toad_Pumba -1912.3333 0.0074 -3400.2538 -424.4129 True
Toad_Nala Toad_Simba 204.3333 0.9996 -1283.5871 1692.2538 False
Toad_Nala Toad_Timon -514.3333 0.9215 -2002.2538 973.5871 False
Toad_Nala Yoshi_Nala 422.3333 0.9706 -1065.5871 1910.2538 False
Toad_Nala Yoshi_Pumba -4481.6667 0.0 -5969.5871 -2993.7462 True
Toad_Nala Yoshi_Simba 1035.0 0.3005 -452.9204 2522.9204 False
Toad_Nala Yoshi_Timon 159.0 0.9999 -1328.9204 1646.9204 False
Toad_Pumba Toad_Simba 2116.6667 0.003 628.7462 3604.5871 True
Toad_Pumba Toad_Timon 1398.0 0.0736 -89.9204 2885.9204 False
Toad_Pumba Yoshi_Nala 2334.6667 0.0011 846.7462 3822.5871 True
Toad_Pumba Yoshi_Pumba -2569.3333 0.0004 -4057.2538 -1081.4129 True
Toad_Pumba Yoshi_Simba 2947.3333 0.0001 1459.4129 4435.2538 True
Toad_Pumba Yoshi_Timon 2071.3333 0.0036 583.4129 3559.2538 True
Toad_Simba Toad_Timon -718.6667 0.7035 -2206.5871 769.2538 False
Toad_Simba Yoshi_Nala 218.0 0.9994 -1269.9204 1705.9204 False
Toad_Simba Yoshi_Pumba -4686.0 0.0 -6173.9204 -3198.0796 True
Toad_Simba Yoshi_Simba 830.6667 0.55 -657.2538 2318.5871 False
Toad_Simba Yoshi_Timon -45.3333 1.0 -1533.2538 1442.5871 False
Toad_Timon Yoshi_Nala 936.6667 0.411 -551.2538 2424.5871 False
Toad_Timon Yoshi_Pumba -3967.3333 0.0 -5455.2538 -2479.4129 True
Toad_Timon Yoshi_Simba 1549.3333 0.0382 61.4129 3037.2538 True
Toad_Timon Yoshi_Timon 673.3333 0.7622 -814.5871 2161.2538 False
Yoshi_Nala Yoshi_Pumba -4904.0 0.0 -6391.9204 -3416.0796 True
Yoshi_Nala Yoshi_Simba 612.6667 0.8331 -875.2538 2100.5871 False
Yoshi_Nala Yoshi_Timon -263.3333 0.9981 -1751.2538 1224.5871 False
Yoshi_Pumba Yoshi_Simba 5516.6667 0.0 4028.7462 7004.5871 True
Yoshi_Pumba Yoshi_Timon 4640.6667 0.0 3152.7462 6128.5871 True
Yoshi_Simba Yoshi_Timon -876.0 0.4887 -2363.9204 611.9204 False
----------------------------------------------------------------------Diese Ergebnisse zeigen uns, welche Kombinationen sich signifikant voneinander unterscheiden. Bei 8 Kombinationen erhalten wir 28 paarweise Vergleiche - deutlich mehr als bei den einfachen Haupteffekten.
Modellreduktion bei nicht-signifikanten Interaktionen
In unserem landwirtschaftlichen Beispiel haben wir eine signifikante Interaktion gefunden. Natürlich kann es aber auch vorkommen, dass die Interaktion nicht signifikant ist. In solchen Fällen wollen wir die Ergebnisse natürlich auch möglichst gut aufbereiten. Eine gängige Herangehensweise ist es das Modell zu vereinfachen, indem wir den Interaktionsterm entfernen. Schauen wir uns dazu ein Beispiel mit dem Palmer Penguins Datensatz an.
Palmer Penguins: Geschlecht und Art
Untersuchen wir den Einfluss von Pinguinart und Geschlecht auf die Schnabellänge:
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Daten vorbereiten
penguins_clean = penguins[['species', 'sex', 'bill_length_mm']].dropna()
penguins_clean species sex bill_length_mm
0 Adelie male 39.1
1 Adelie female 39.5
2 Adelie female 40.3
4 Adelie female 36.7
5 Adelie male 39.3
.. ... ... ...
339 Chinstrap male 55.8
340 Chinstrap female 43.5
341 Chinstrap male 49.6
342 Chinstrap male 50.8
343 Chinstrap female 50.2
[333 rows x 3 columns]
Schauen wir uns wieder einige Kennzahlen an:
(
penguins_clean.groupby(['species', 'sex'])['bill_length_mm']
.agg(mean=lambda x: round(x.mean(), 1), sd=lambda x: round(x.std(), 1), n='count')
.reset_index()
.sort_values('mean', ascending=False)
) species sex mean sd n
3 Chinstrap male 51.1 1.6 34
5 Gentoo male 49.5 2.7 61
2 Chinstrap female 46.6 3.1 34
4 Gentoo female 45.6 2.1 58
1 Adelie male 40.4 2.3 73
0 Adelie female 37.3 2.0 73Und visualisieren die Daten:
# Visualisierung der Pinguin-Daten
plot_two_way_data(penguins_clean, 'species', 'sex', 'bill_length_mm',
'Pinguinart', 'Geschlecht', 'Schnabellänge (mm)',
factor1_colors=['#9b5de5', '#00bbf9'],
title='Schnabellänge nach Geschlecht und Pinguinart')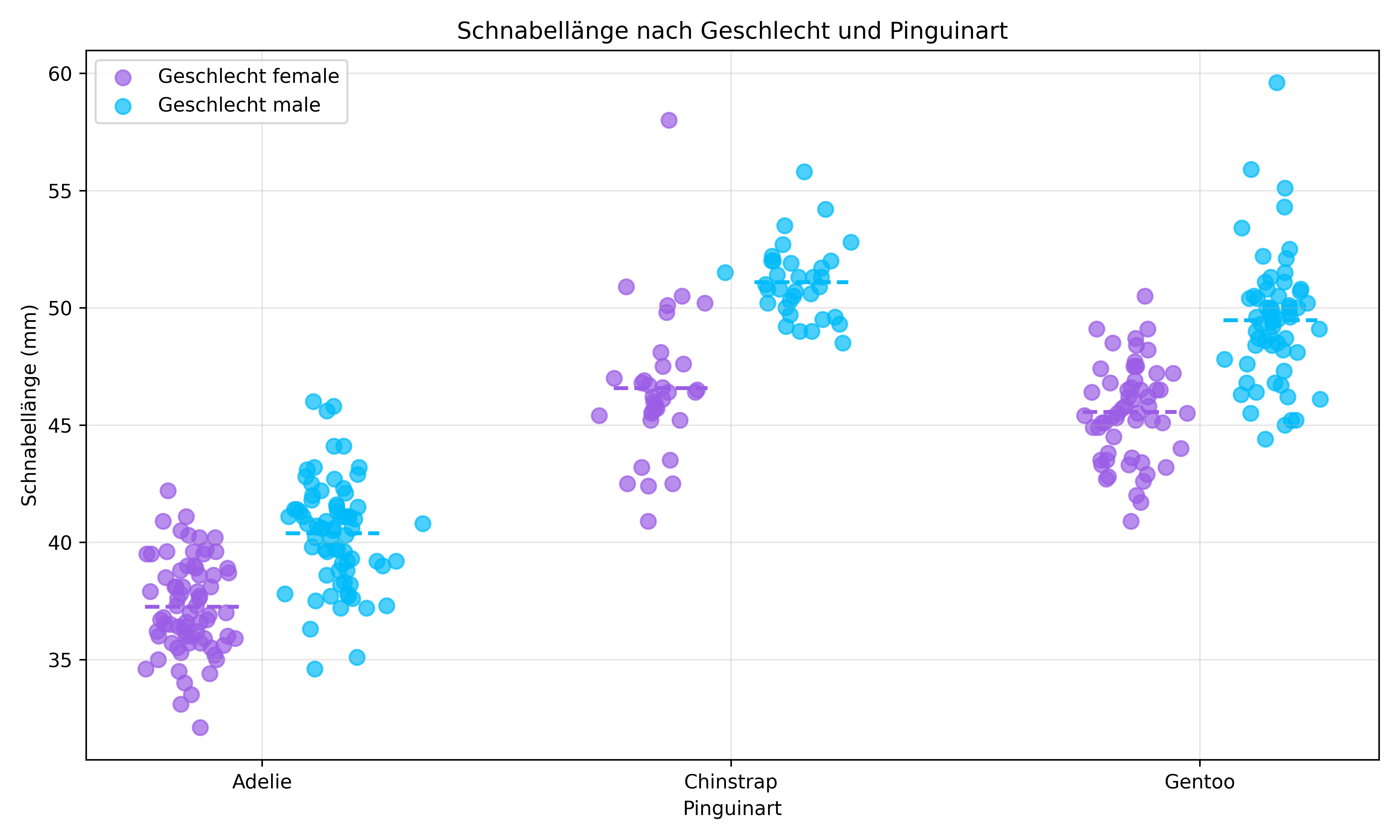
Vollständige ANOVA mit Interaktion
Führen wir zunächst die vollständige ANOVA mit Interaktionsterm durch:
# Modell mit Interaktion
model_full = smf.ols('bill_length_mm ~ C(species) * C(sex)', data=penguins_clean).fit()
anova_full = sm.stats.anova_lm(model_full, typ=3)
print("ANOVA mit Interaktion:")
print(anova_full)ANOVA mit Interaktion:
sum_sq df F PR(>F)
Intercept 101333.041644 1.0 18898.747693 2.299770e-291
C(species) 3088.109987 2.0 287.968320 7.561238e-73
C(sex) 358.244452 1.0 66.813069 6.636406e-15
C(species):C(sex) 24.494427 2.0 2.284122 1.034865e-01
Residual 1753.338642 327.0 NaN NaNDie Ergebnisse zeigen:
- Haupteffekt Species: Hochsignifikant (p < 0.001) - die Pinguinarten unterscheiden sich deutlich in der Schnabellänge
- Haupteffekt Sex: Hochsignifikant (p < 0.001) - Männchen und Weibchen haben unterschiedliche Schnabellängen
- Interaktionseffekt: Nicht signifikant (p > 0.05) - der Geschlechtsunterschied ist in allen Arten ähnlich
Da die Interaktion nicht signifikant ist, können wir das Modell vereinfachen. Dies entspricht einem der fünf Grundszenarien, die wir zu Beginn des Kapitels kennengelernt haben: Beide Haupteffekte sind vorhanden, aber keine Interaktion.
Modellreduktion: Entfernung der Interaktion
Wenn die Interaktion nicht signifikant ist, passt ein additives Modell besser zu den Daten. Wir entfernen den Interaktionsterm:
# Reduziertes Modell ohne Interaktion
model_reduced = smf.ols('bill_length_mm ~ C(species) + C(sex)', data=penguins_clean).fit()
anova_reduced = sm.stats.anova_lm(model_reduced, typ=3)
print("ANOVA ohne Interaktion:")
print(anova_reduced)ANOVA ohne Interaktion:
sum_sq df F PR(>F)
Intercept 138769.908899 1.0 25680.307577 2.727713e-314
C(species) 6975.591607 2.0 645.440137 1.314575e-114
C(sex) 1135.683888 1.0 210.165963 3.597005e-37
Residual 1777.833069 329.0 NaN NaNDas reduzierte Modell ist einfacher zu interpretieren. Beide Haupteffekte bleiben hochsignifikant, was bedeutet:
- Die drei Pinguinarten haben unterschiedliche Schnabellängen
- Männchen haben andere Schnabellängen als Weibchen
- Wichtig: Der Geschlechtsunterschied ist für alle Arten etwa gleich groß (additive Effekte)
Interaktionsplot für die Pinguin-Daten
Schauen wir uns den Interaktionsplot an, um zu verstehen, warum keine Interaktion vorliegt:
# Interaktionsplot für Pinguin-Daten
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
arten = ['Adelie', 'Chinstrap', 'Gentoo']
geschlechter = ['female', 'male']
colors = ['#9b5de5', '#00bbf9']
for i, sex in enumerate(geschlechter):
means = []
for species in arten:
mean_val = penguins_clean[(penguins_clean['sex'] == sex) &
(penguins_clean['species'] == species)]['bill_length_mm'].mean()
means.append(mean_val)
ax.plot(range(len(arten)), means, marker='o', linewidth=2, markersize=8,
label=f'{sex.capitalize()}', color=colors[i])
ax.set_xlabel('Pinguinart')
ax.set_ylabel('Mittlere Schnabellänge (mm)')
ax.set_title('Interaktionsplot: Geschlecht × Pinguinart')
ax.set_xticks(range(len(arten)))
ax.set_xticklabels(arten)
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()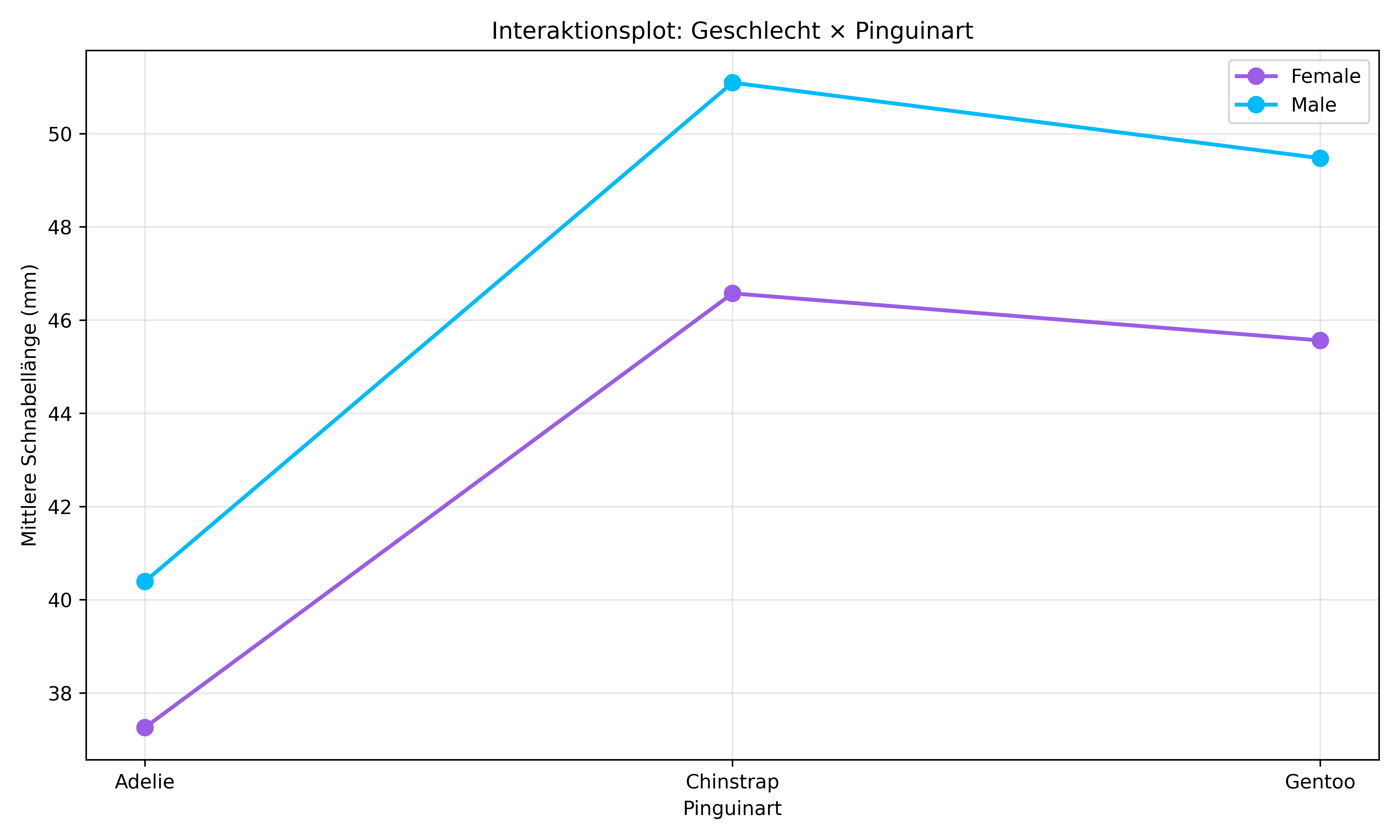
Die Linien verlaufen nahezu parallel, was die fehlende Interaktion bestätigt. Der Geschlechtsunterschied ist bei allen drei Arten etwa gleich groß - Männchen haben durchweg längere Schnäbel als Weibchen, und dieser Unterschied ist konstant über alle Arten hinweg.
Post-hoc-Tests für die Haupteffekte
Da beide Haupteffekte signifikant sind, können wir nun separate Post-hoc-Tests für jeden Faktor durchführen:
# Post-hoc-Test für Pinguinarten
print("Tukey-Test für Pinguinarten:")
tukey_species = pairwise_tukeyhsd(
endog=penguins_clean['bill_length_mm'],
groups=penguins_clean['species'],
alpha=0.05
)
print(tukey_species)Tukey-Test für Pinguinarten:
Multiple Comparison of Means - Tukey HSD, FWER=0.05
==========================================================
group1 group2 meandiff p-adj lower upper reject
----------------------------------------------------------
Adelie Chinstrap 10.0099 0.0 8.9828 11.0369 True
Adelie Gentoo 8.7441 0.0 7.8801 9.6081 True
Chinstrap Gentoo -1.2658 0.0148 -2.3292 -0.2023 True
----------------------------------------------------------# Post-hoc-Test für Geschlecht
print("Tukey-Test für Geschlecht:")
tukey_sex = pairwise_tukeyhsd(
endog=penguins_clean['bill_length_mm'],
groups=penguins_clean['sex'],
alpha=0.05
)
print(tukey_sex)Tukey-Test für Geschlecht:
Multiple Comparison of Means - Tukey HSD, FWER=0.05
================================================
group1 group2 meandiff p-adj lower upper reject
------------------------------------------------
female male 3.7578 0.0 2.649 4.8666 True
------------------------------------------------Interpretation der Ergebnisse
Die Post-hoc-Tests zeigen:
Für Pinguinarten:
- Alle drei Arten unterscheiden sich signifikant voneinander in der Schnabellänge
- Chinstrap-Pinguine haben die längsten Schnäbel, gefolgt von Gentoo, dann Adelie
Für Geschlecht:
- Männchen haben signifikant längere Schnäbel als Weibchen
- Der Unterschied beträgt etwa 3-4 mm im Durchschnitt
Praktische Interpretation:
Da keine Interaktion vorliegt, können wir einfache Aussagen treffen:
- “Chinstrap-Pinguine haben die längsten Schnäbel, unabhängig vom Geschlecht”
- “Männchen haben längere Schnäbel als Weibchen, unabhängig von der Art”
Diese einfache Interpretation wäre bei einer signifikanten Interaktion nicht möglich gewesen.
Fazit
Zusammenfassend haben wir in diesem Kapitel zwei verschiedene Szenarien gesehen:
Landwirtschaftliches Experiment (signifikante Interaktion):
- Vollständiges Modell beibehalten:
y ~ A + B + A:B - Post-hoc-Test für alle Kombinationen durchführen
- Komplexere Interpretation erforderlich: “Es kommt darauf an…”
Palmer Penguins (keine signifikante Interaktion):
- Modell reduzieren:
y ~ A + B - Separate Post-hoc-Tests für jeden signifikanten Haupteffekt
- Einfachere Interpretation möglich: additive Effekte
Diese Flexibilität im Modellierungsansatz ist ein wichtiger Vorteil der zweifaktoriellen ANOVA. Je nach Datenlage können wir das am besten passende Modell wählen und entsprechend interpretieren. Im Fall der Palmer Penguins haben wir gesehen, dass sowohl Pinguinart als auch Geschlecht einen signifikanten Einfluss auf die Schnabellänge haben, diese Effekte aber additiv und nicht interaktiv sind.
Bisher haben wir in allen ANOVA-Beispielen typ=3 verwendet, ohne zu erklären warum. Tatsächlich gibt es drei verschiedene Arten von ANOVAs, welche man auch wirklich I, II und III nennt. Sie unterscheiden sich darin wie genau man die Summe der Quadrate berechnet, was wiederum eine Auswirkung darauf hat wie man mit unbalancierten Designs/Daten umgeht. “Unbalanciert” meint Situationen, in denen nicht alle Faktor-Kombinationen gleich viele Beobachtungen haben.
Das Problem unbalancierter Daten
In einem balancierten Design haben alle Gruppen/Kombinationen die gleiche Anzahl an Beobachtungen. In unserem landwirtschaftlichen Beispiel hatten wir eben das: genau 3 Beobachtungen pro Kombination (2×4×3 = 24 total). In der Praxis sind Designs jedoch oft unbalanciert - manche Gruppen haben mehr Beobachtungen als andere, oder es fehlen sogar ganze Kombinationen. Beim Pinguinbeispiel war es ja auch so, dass nicht alle Kombinationen von Pinguinart und Geschlecht gleich viele Beobachtungen hatten.
Bei unbalancierten Designs überlappen sich die Effekte der Faktoren, und es entstehen verschiedene Möglichkeiten, die Varianz aufzuteilen.
Die drei Typen
Typ I (Sequential/Hierarchical SS):
- Testet jeden Term in der Reihenfolge, wie er ins Modell eingegeben wurde
- Jeder Term wird nur für die vorhergehenden Terme kontrolliert
- Problem: Die Ergebnisse hängen von der Reihenfolge der Terme ab
- Verwendung: Nur bei spezifischen hierarchischen Hypothesen
Typ II (Marginal SS ohne höhere Ordnung):
- Jeder Term wird für alle anderen Terme derselben oder niedrigerer Ordnung kontrolliert
- Haupteffekte werden für andere Haupteffekte kontrolliert, aber nicht für Interaktionen
- Annahme: Keine Interaktionen höherer Ordnung
- Verwendung: Wenn keine signifikanten Interaktionen erwartet werden
Typ III (Marginal SS mit höherer Ordnung):
- Jeder Term wird für alle anderen Terme im Modell kontrolliert
- Auch Haupteffekte werden für alle Interaktionen kontrolliert
- Vorteil: Ergebnisse sind unabhängig von der Reihenfolge der Terme
- Nachteil: Hat weniger Power, wenn keine Interaktionen vorliegen
- Verwendung: Standard in vielen Statistikprogrammen (SPSS, SAS)
Praktische Empfehlungen
Für balancierte Designs:
- Alle drei Typen liefern identische Ergebnisse
- Die Wahl spielt keine Rolle
Für unbalancierte Designs:
- Typ II: Empfohlen, wenn keine Interaktionen im Modell sind oder diese nachweislich nicht signifikant sind
- Typ III: Empfohlen, wenn Interaktionen im Modell sind oder vermutet werden
- Typ I: Nur bei spezifischen hierarchischen Fragestellungen
Implementation in Python
# Beispiel mit unbalancierten Daten (entferne einige Beobachtungen)
df_unbalanced = df.drop([0, 5, 10, 15]) # Entferne 4 Beobachtungen
# Modell anpassen
model = smf.ols('ertrag ~ C(duenger) * C(sorte)', data=df_unbalanced).fit()
# Verschiedene ANOVA-Typen vergleichen
print("Typ I (Sequential):")
print(sm.stats.anova_lm(model, typ=1))
print("\nTyp II (Marginal ohne höhere Ordnung):")
print(sm.stats.anova_lm(model, typ=2))
print("\nTyp III (Marginal mit höherer Ordnung):")
print(sm.stats.anova_lm(model, typ=3))Fazit: Für die meisten praktischen Anwendungen ist Typ II ausreichend. Wenn ihr unsicher seid oder Interaktionen im Modell habt, verwendet Typ III. Typ I sollte nur bei sehr spezifischen theoretischen Überlegungen zur Reihenfolge der Effekte verwendet werden.
Übungen
Übung 1
Importiere den Vision-Datensatz und führe eine zweifaktorielle ANOVA durch, um den Einfluss von Profession und Geschlecht auf die Körpergröße zu untersuchen.
# Vision Datensatz laden
pfad = "https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/vision/vision_fixed.csv"
vision = pd.read_csv(pfad, sep=';')Datenexploration: Entferne fehlende Werte für die Variablen Height, Profession und Gender. Berechne Gruppenmittelwerte und Standardabweichungen für Height pro Kombinationen der Faktoren. Erstelle auch eine Visualisierung der Daten (z.B. Jitter-Plot).
-
Zweifaktorielle ANOVA: Führe eine zweifaktorielle ANOVA mit dem Modell durch. Interpretiere die Ergebnisse:
- Ist der Haupteffekt von Profession signifikant?
- Ist der Haupteffekt von Gender signifikant?
- Liegt eine signifikante Interaktion vor?
Post-hoc-Tests: Basierend auf den ANOVA-Ergebnissen, entscheide ob das Modell vereinfacht werden sollte und welche Post-hoc-Tests angemessen sind.
-
Interpretation: Fasse die praktischen Schlussfolgerungen zusammen. Gibt es Unterschiede in der Körpergröße zwischen:
- Students und Professionals?
- Männern und Frauen?
- Hängen diese Effekte voneinander ab?