import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
np.random.seed(1) # damit die Zufallszahlen reproduzierbar sindKorrelation
Jeder hat zumindest eine intuitive Vorstellung davon, was Korrelation ist: Zwei Dinge hängen irgendwie zusammen oder bewegen sich gemeinsam. Der Begriff “Korrelation” wird im Alltag oft verwendet, manchmal jedoch unpräzise. Als Data Scientists müssen wir ein klares Verständnis davon haben, was Korrelation statistisch bedeutet, wie sie berechnet wird und - besonders wichtig - was sie uns sagt und was sie uns nicht sagt.
In diesem Kapitel werden wir zunächst den klassischen Pearson-Korrelationskoeffizienten betrachten und sehen, wie wir ihn in Python berechnen können. Wir werden auch die statistische Signifikanz von Korrelationen untersuchen und alternative Korrelationsmaße wie die Spearman-Rangkorrelation kennenlernen. Schließlich werden wir uns damit beschäftigen, wie man Korrelationsmatrizen erstellt und visualisiert, was ein wichtiges Werkzeug in der explorativen Datenanalyse ist.
Grundkonzepte der Korrelation
Ein quantitatives Maß für den Zusammenhang zwischen zwei Variablen ist der Korrelationskoeffizient. Wenn von Korrelation (\(\rho\) oder \(r\)) in der Statistik die Rede ist, bezieht man sich meistens auf den Korrelationskoeffizient nach Bravais-Pearson, der ein Maß für den linearen Zusammenhang zwischen zwei numerischen Variablen darstellt.
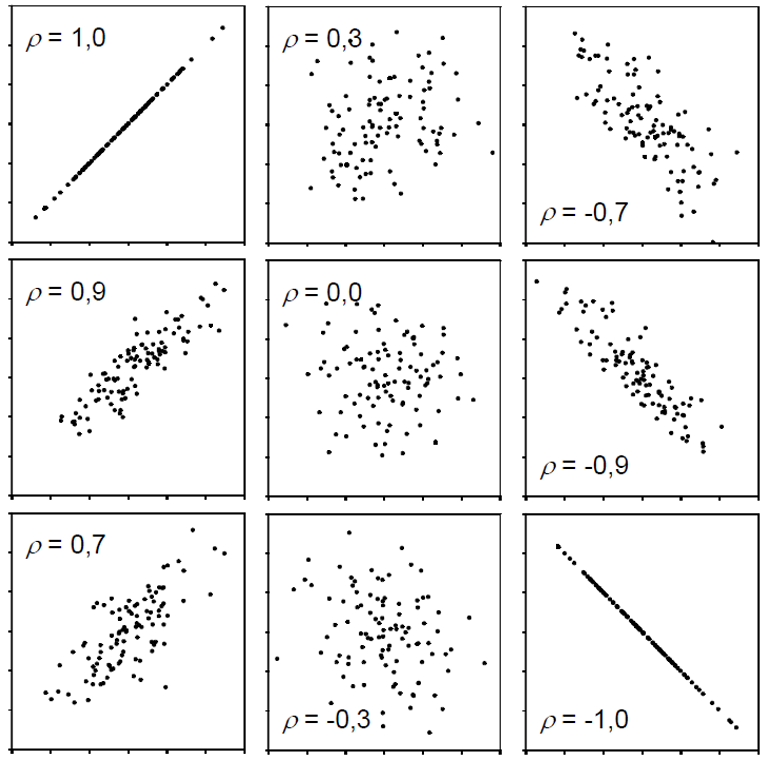
Der Korrelationskoeffizient kann nur Werte zwischen -1 und 1 annehmen:
- \(\rho = -1\) - Perfekte negative Korrelation
- \(\rho = 0\) - Keine Korrelation
- \(\rho = 1\) - Perfekte positive Korrelation
Je weiter der Koeffizient von 0 entfernt ist, desto stärker ist der Zusammenhang. Hier ein paar Beispiele:
Vereinfacht ausgedrückt bedeutet eine positive Korrelation: “Wenn eine Variable größer wird, wird die andere tendenziell auch größer”. Eine negative Korrelation bedeutet: “Wenn eine Variable größer wird, wird die andere tendenziell kleiner”. Wichtig zu verstehen ist, dass die Reihenfolge der beiden Variablen keine Rolle spielt. Die Korrelation zwischen X und Y ist dieselbe wie die Korrelation zwischen Y und X. Eine Korrelation ist also kein Modell1 und kann nicht für Vorhersagen verwendet werden.
Korrelation ≠ Kausalität
Ein kritisch wichtiger Grundsatz in der Statistik lautet: “Korrelation impliziert nicht Kausalität”: Nur weil zwei Variablen X und Y korreliert sind, bedeutet das nicht automatisch, dass eine die andere verursacht. Es könnte z.B. sein, dass:
- \(X\) verursacht \(Y\)
- \(Y\) verursacht \(X\)
- Ein dritter Faktor \(Z\) verursacht sowohl \(X\) als auch \(Y\)
- Die Korrelation ist rein zufällig
Die Website Spurious Correlations zeigt humorvolle Beispiele von starken Korrelationen zwischen völlig unzusammenhängenden Dingen.
Ja, gleich kommen mathematische Formeln, aber keine Sorge, man darf diese Formeln auch einfach nur überfliegen. Der Punkt ist aber, dass Berechnungen wie die folgenden im Endeffekt natürlich keine Magie sind, sondern etwas, das man auch einfach mit Stift, Papier und etwas Zeit berechnen könnte.
Pearson-Korrelationskoeffizient
Wie gesagt wird in der Regel diese Methode verwendet, wenn schlichtweg davon die Rede ist was die Korrelation ist. Die Formel für den Pearson-Korrelationskoeffizienten ist:
\[r = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i - \bar{x})^2 \sum_{i=1}^{n} (y_i - \bar{y})^2}}\]
Wobei \(\bar{x}\) und \(\bar{y}\) die Mittelwerte der Variablen \(x\) und \(y\) sind. Eine alternative Formulierung ist, dass der Pearson-Korrelationskoeffizient die Kovarianz der beiden Variablen geteilt durch das Produkt ihrer Standardabweichungen ist:
\[r = \frac{cov(X,Y)}{\sigma_X \sigma_Y}\]
Berechnung der Korrelation in Python
Zunächst erzeugen wir Beispieldaten. Der resultierende DataFrame hat je 100 Werte für die Variablen x, y1, y2, y3 und y4, wobei jede y-Variable unterschiedlich stark mit x korreliert ist:
# Erzeugen korrelierter Daten
n = 100
x = np.random.normal(0, 1, n) # 100 Zufallszahlen aus Normalverteilung
y1 = x + np.random.normal(0, 0.5, n) # Starke positive Korrelation
y2 = x + np.random.normal(0, 2, n) # Schwache positive Korrelation
y3 = -x + np.random.normal(0, 0.5, n) # Starke negative Korrelation
y4 = np.random.normal(0, 1, n) # Keine Korrelation
# In DataFrame speichern
df = pd.DataFrame({'x': x, 'y1': y1, 'y2': y2, 'y3': y3, 'y4': y4})
# Ersten Zeilen anzeigen
df.head() x y1 y2 y3 y4
0 1.624345 1.400781 0.822589 -0.591454 -1.306534
1 -0.611756 0.000497 1.036255 -0.123822 0.076380
2 -0.528172 -0.326426 -1.652783 0.113086 0.367232
3 -1.072969 -0.776179 2.836788 0.632680 1.232899
4 0.865408 0.317952 -1.798496 -1.004956 -0.422857Die eben verwendete Funktion np.random.normal(mean, std, size) erzeugt Zufallszahlen, die einer Normalverteilung folgen. Die Parameter sind:
-
mean: Mittelwert der Normalverteilung (hier 0) -
std: Standardabweichung der Normalverteilung (variiert je nach Zeile) -
size: Anzahl der zu erzeugenden Zufallszahlen (hier 100)
Je kleiner die Standardabweichung, desto “näher” liegen die erzeugten Zufallswerte am Originalwert.
Außerdem haben wir ganz oben beim Import von Modulen np.random.seed(42) verwendet, um sicherzustellen, dass die Zufallszahlen reproduzierbar sind. Das bedeutet, dass jeder, der diesen Code ausführt, die gleichen Zufallszahlen erhält, da alle mit demselben “Seed” beginnen.
fig, axs = plt.subplots(2, 2, layout="tight")
fig.set_size_inches(8,8)
axs[0, 0].scatter(x, y1)
axs[0, 0].set_title('Starke positive Korrelation')
axs[0, 1].scatter(x, y2)
axs[0, 1].set_title('Schwache positive Korrelation')
axs[1, 0].scatter(x, y3)
axs[1, 0].set_title('Starke negative Korrelation')
axs[1, 1].scatter(x, y4)
axs[1, 1].set_title('Keine Korrelation')
plt.show()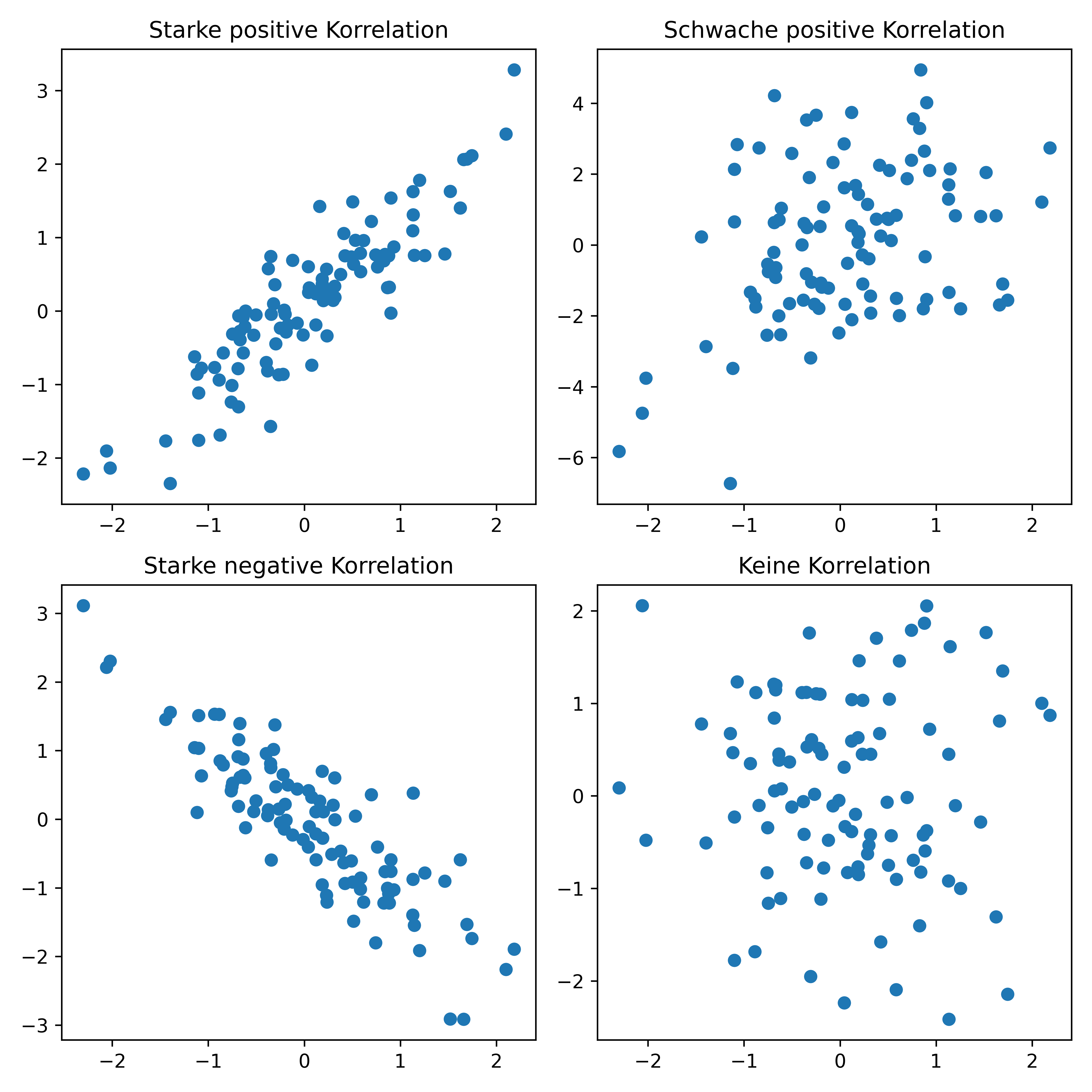
In Python gibt es mehrere Möglichkeiten, Korrelationen zu berechnen - selbst mit den Modulen, die wir bisher kennengelernt haben. Hier sind ein paar Beispiele wie wir die Korrelation erstmal nur zwischen unserer Variable x und der stark positiv korrelierten Variable y1 berechnen könnten:
# NumPy-Methode
np.corrcoef(x, y1)[0, 1]np.float64(0.8942788270367769)# Pandas-Methode
df['x'].corr(df['y1'])np.float64(0.8942788270367769)# SciPy-Methode (mit p-Wert)
stats.pearsonr(x, y1)PearsonRResult(statistic=np.float64(0.8942788270367766), pvalue=np.float64(5.387077880064751e-36))Wie wir sehen, liefern alle drei Methoden das gleiche Ergebnis für den Korrelationskoeffizienten, nämlich, dass x und x1 eine Korrelation von 0,87 aufweisen. Der Vorteil der SciPy-Methode liegt darin, dass sie zusätzlich einen p-Wert zurückgibt, der angibt, ob die beobachtete Korrelation statistisch signifikant ist. Was der p-Wert genau ist besprechen wir im nächsten Kapitel. Die Kurzfassung ist, dass er angibt ob eine Korrelation zufällig entstanden sein könnte oder nicht - falls der p-Wert sehr klein ist, dann ist die Antwort “eher nicht” und die Korrelation gilt als “statistisch signifikant”.
Da die SciPy-Methode uns sowohl den Korrelationskoeffizienten als auch den p-Wert liefert, werden wir uns im Folgenden auf diese Methode konzentrieren.
Hier berechnen wir die Korrelationen für alle unsere Beispieldaten:
# Berechnung aller Korrelationen mit SciPy
corr_y1, p_y1 = stats.pearsonr(x, y1)
corr_y2, p_y2 = stats.pearsonr(x, y2)
corr_y3, p_y3 = stats.pearsonr(x, y3)
corr_y4, p_y4 = stats.pearsonr(x, y4)
print(f"x-y1: r={corr_y1:.4f}, p={p_y1:.4e} - Starke positive Korrelation:")
print(f"x-y2: r={corr_y2:.4f}, p={p_y2:.4e} - Schwache positive Korrelation")
print(f"x-y3: r={corr_y3:.4f}, p={p_y3:.4e} - Starke negative Korrelation")
print(f"x-y4: r={corr_y4:.4f}, p={p_y4:.4f} - Keine Korrelation")x-y1: r=0.8943, p=5.3871e-36 - Starke positive Korrelation:
x-y2: r=0.3750, p=1.2106e-04 - Schwache positive Korrelation
x-y3: r=-0.8692, p=9.7771e-32 - Starke negative Korrelation
x-y4: r=-0.0462, p=0.6481 - Keine KorrelationNatürlich ist die Korrelation zwischen x und y4 nicht exakt 0, aber eben mehr oder weniger. Der p-Wert ist hier auch relativ hoch, was darauf hindeutet, dass die Korrelation durchaus zufällig entstanden sein könnte. Mehr dazu wie gesagt demnächst.
Korrelationsmatrizen
In der Praxis haben wir es oft mit mehreren Variablen zu tun und möchten alle paarweisen Korrelationen auf einmal berechnen. Dafür sind Korrelationsmatrizen ideal.
Eine Korrelationsmatrix ist eine quadratische Matrix, die die Korrelationskoeffizienten zwischen allen Paaren von Variablen enthält. Pandas macht es sehr einfach, eine Korrelationsmatrix zu berechnen:
# Berechne Korrelationsmatrix
correlation_matrix = df.corr()
print(correlation_matrix) x y1 y2 y3 y4
x 1.000000 0.894279 0.374987 -0.869196 -0.046202
y1 0.894279 1.000000 0.419069 -0.788530 -0.073340
y2 0.374987 0.419069 1.000000 -0.351640 0.014928
y3 -0.869196 -0.788530 -0.351640 1.000000 -0.095802
y4 -0.046202 -0.073340 0.014928 -0.095802 1.000000Die Diagonale enthält immer den Wert 1, da jede Variable perfekt mit sich selbst korreliert ist. Das obere und untere Dreieck der Matrix sind Spiegelbilder voneinander, da die Korrelation zwischen x und y dieselbe ist wie die zwischen y und x.
Visualisierung von Korrelationsmatrizen
Eine Korrelationsmatrix lässt sich am besten visuell als Heatmap darstellen.
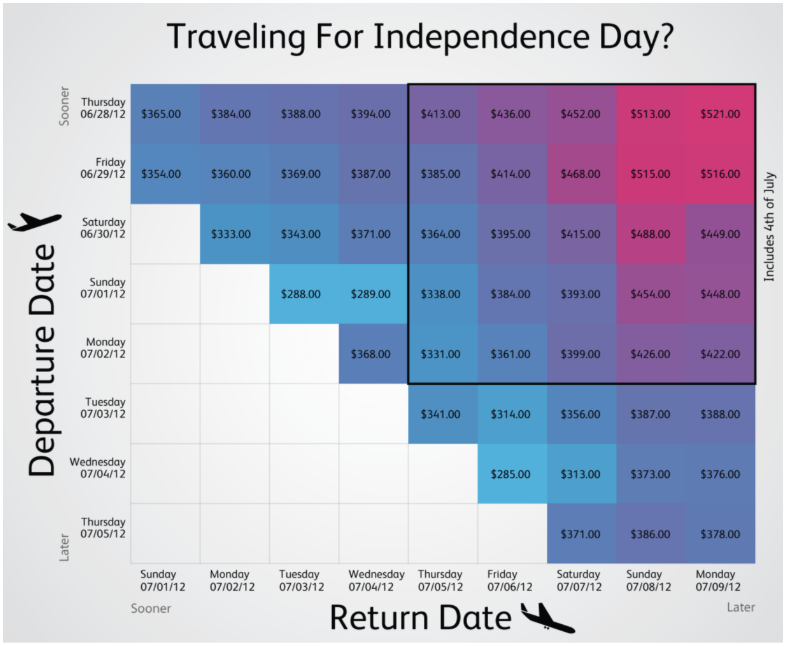
Eine Heatmap ist eine grafische Darstellung von Daten, bei der Werte durch Farben repräsentiert werden. Je intensiver die Farbe, desto höher (oder niedriger) der Datenwert. Bei Heatmaps werden die einzelnen farbigen Rechtecke, die jeweils einen Datenpunkt darstellen als Tiles (oder Zellen) bezeichnet. Heatmaps werden häufig verwendet für: (i) Korrelationsmatrizen (wie hier gezeigt), (ii) Darstellung von Mustern in großen Datensätzen (iii) Darstellung von zeitlichen oder räumlichen Verteilungen.
Zur Erweiterung einer Heatmap kann ein Dendrogramm hinzugefügt werden – eine baumartige Struktur, die hierarchische Cluster visualisiert und damit verwandte Variablen durch Umordnung der Zeilen und Spalten nebeneinander gruppiert, sodass ähnliche Datenpunkte in der Heatmap näher beieinander liegen.
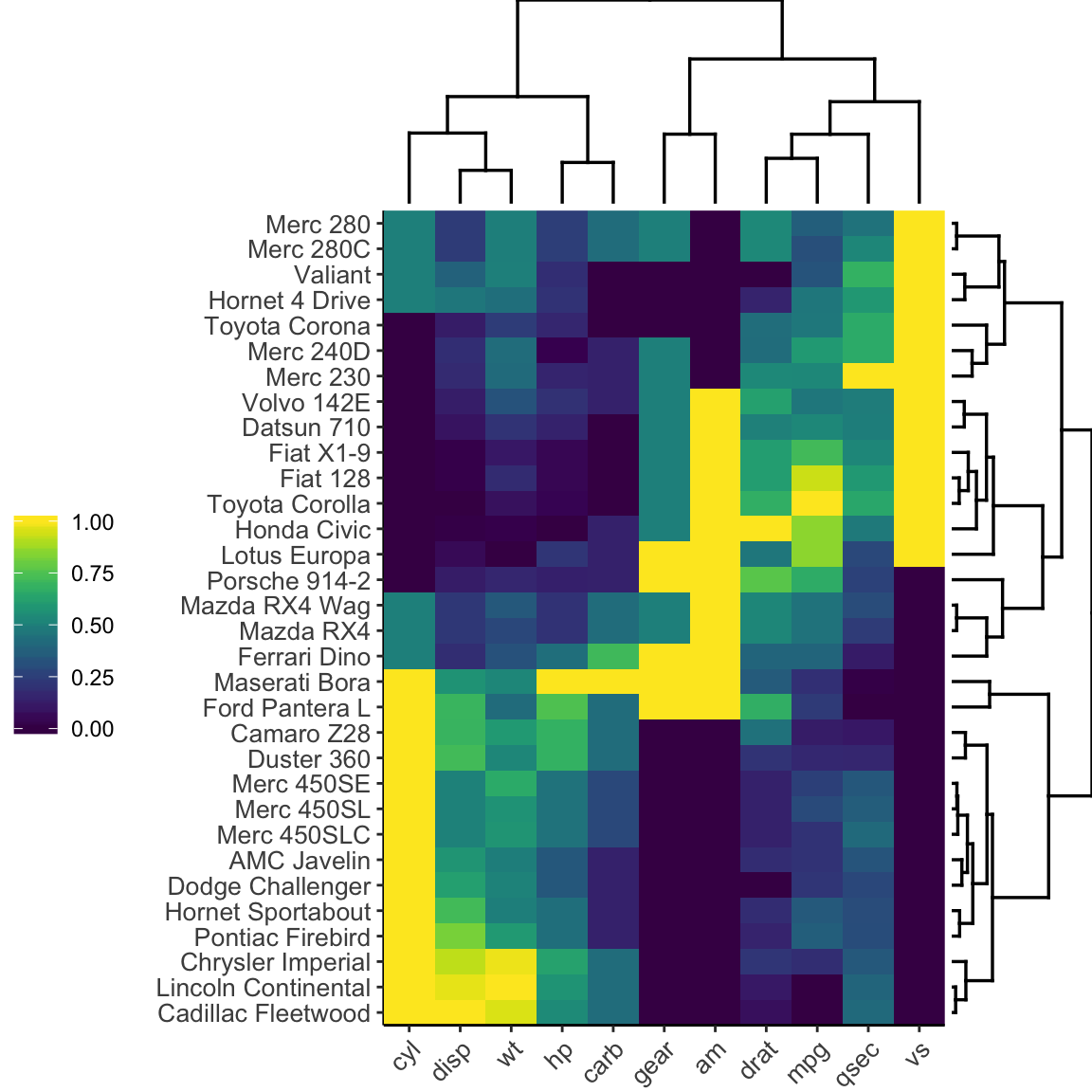
Eine Heatmap für correlation_matrix zu erzeugen ist sehr komfortabel möglich mit sns.heatap(). (Wir werden aber direkt im nächsten Kapitel die folgende Abbildung auch ohne seaborn und nur mit matplotlib nachbauen.)
# Erstellen einer Heatmap mit Seaborn
fig, ax = plt.subplots()
sns.heatmap(
data=correlation_matrix,
square=True, # forciert eine quadratische Form der Tiles
annot=True, # Schreibt Wert auf jedes Tile
cmap='coolwarm', # Name einer der Farbpaletten
vmin=-1, # Legende Start - Standard: Kleinster Wert in Daten
vmax=1, # Legende Ende - Standard: Größter Wert in Daten
center=0, # Legende Mitte
ax=ax # Explizit angeben, dass wir unsere ax verwenden wollen
)
plt.show()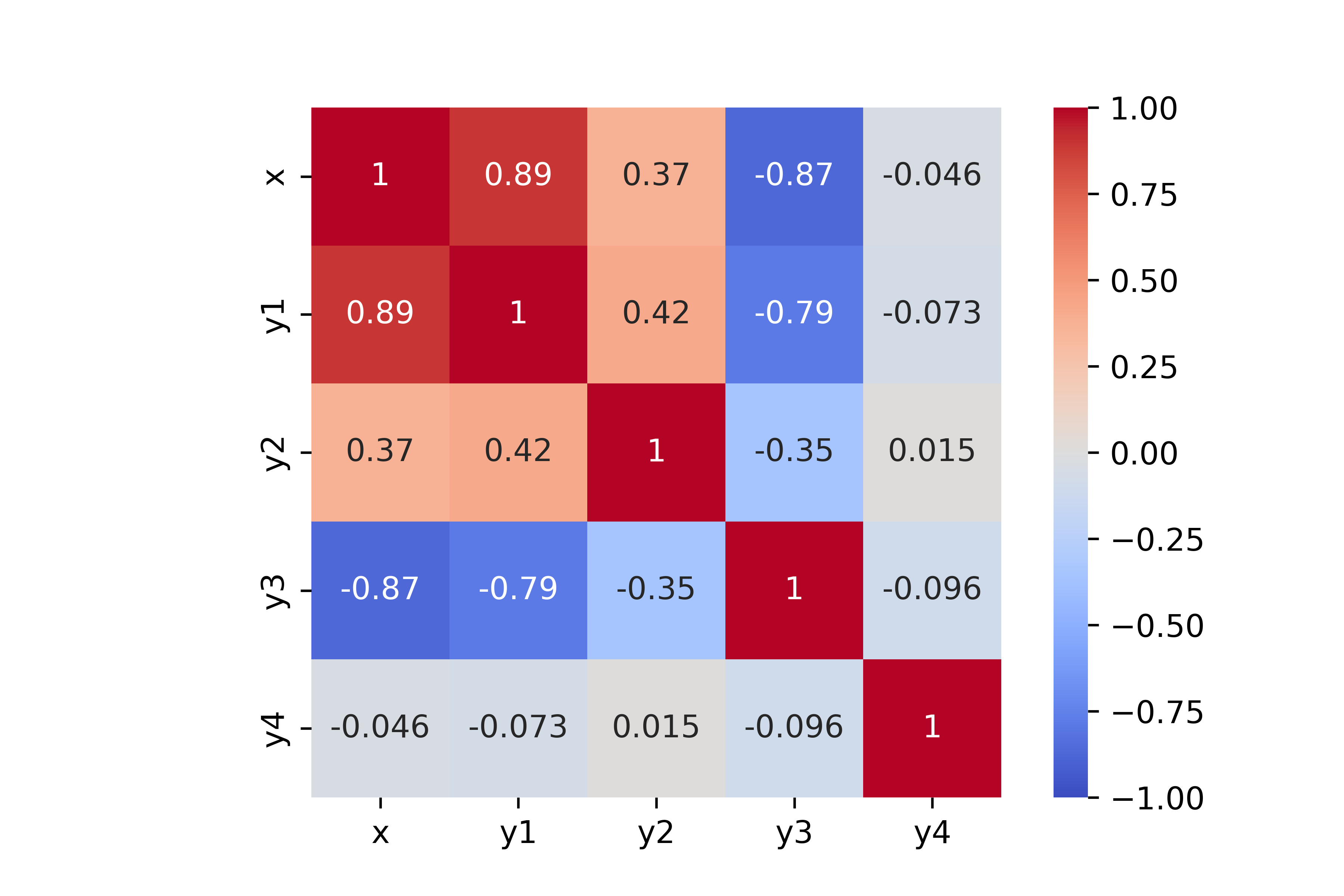
In dieser Heatmap:
- Dunkelblaue Felder repräsentieren starke negative Korrelationen
- Dunkelrote Felder repräsentieren starke positive Korrelationen
- Weiße Felder repräsentieren keine Korrelation
- Die Zahlen in den Feldern sind die genauen Korrelationskoeffizienten
Abgesehen davon, dass man also auf einen Blick alle paarweisen Korrelationen mit solch einer Heatmap schnell erfassen kann, sieht man ggf. zusätzlich auch Muster, also Cluster/Gruppen von Variablen die z.B. stärker miteinander korrelieren als andere.
Alternative Korrelationsmethoden
Der Pearson-Korrelationskoeffizient ist nicht immer die beste Wahl. Er setzt nämlich voraus, dass:
- Die Beziehung zwischen den Variablen linear ist
- Die Variablen kontinuierlich und normalverteilt sind
- Die Daten keine bedeutenden Ausreißer enthalten
Wenn diese Voraussetzungen nicht erfüllt sind, können alternative Korrelationsmethoden besser geeignet sein. Hier erzeugen wir y5 und y6 so, dass eben solch ein Fall eintritt:
y5 = np.exp(x) + np.random.normal(0, 0.1, n)
underlying = x + np.random.normal(0, 0.3, n)
y6 = pd.cut(underlying, bins=5, labels=[1, 2, 3, 4, 5]).astype(int)fig, axs = plt.subplots(1, 3, figsize=(8, 4), layout="tight")
axs[0].scatter(x, y1)
axs[0].set_title('Lineare Beziehung (y1)')
axs[1].scatter(x, y5, color='orange')
axs[1].set_title('Nichtlineare Beziehung (y5)')
axs[2].scatter(x, y6, color='orange')
axs[2].set_title('Ordinale Daten (y6)')
plt.show()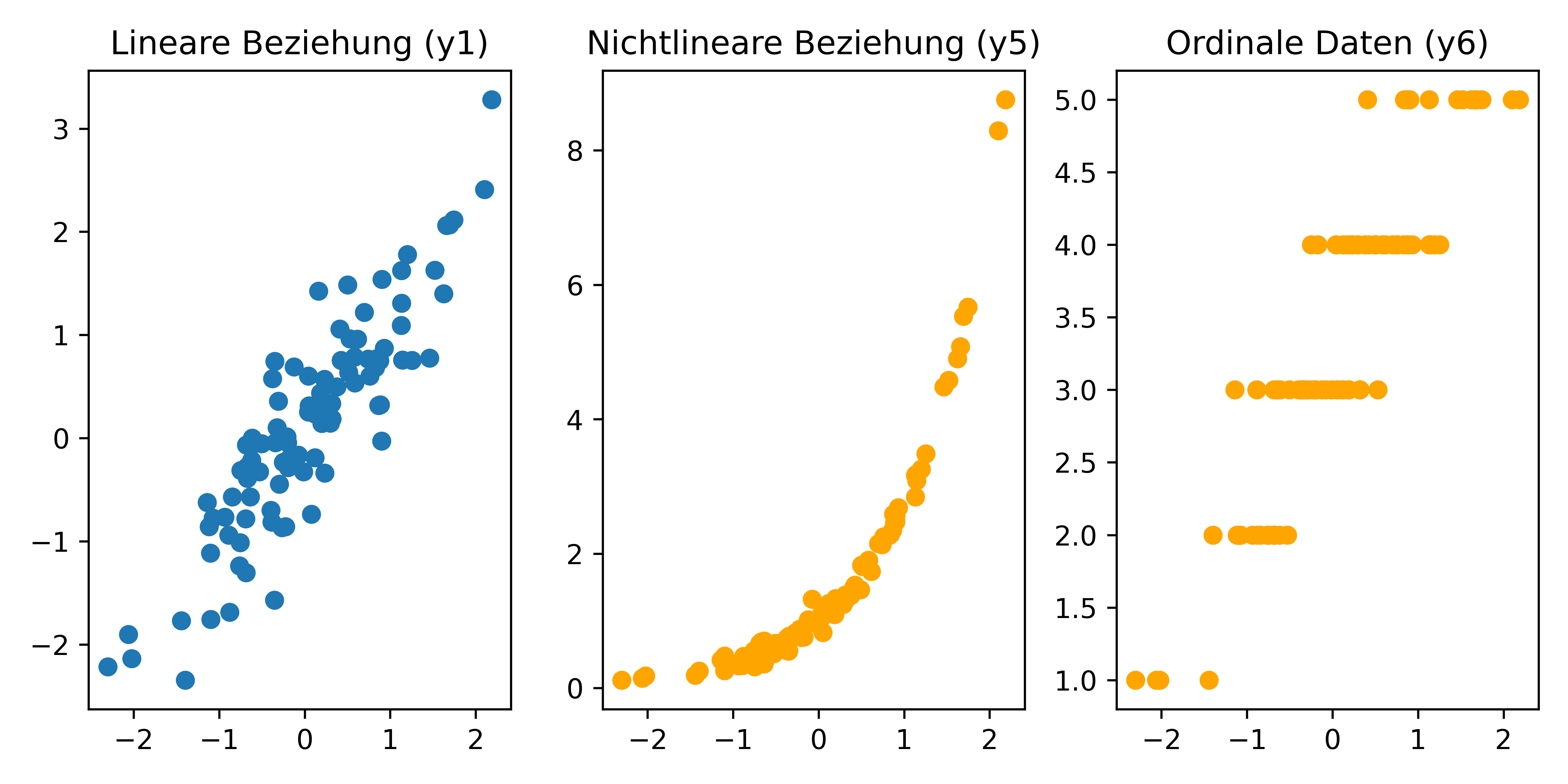
Wie man sieht handelt es sich bei der Beziehung von x und y5 eben nicht um eine lineare, aber dennoch monotone Beziehung. Das bedeutet, dass die Werte von x und y5 zwar stets gemeinsam steigen (=monoton), aber nicht in einem konstanten Verhältnis (=nicht linear). Die Beziehung zwischen x und y6 ist ordinal, da die Werte von y6 zwar Zahlen sind, aber nur die Reihenfolge und nicht die Differenz zwischen den Werten eine Bedeutung hat. Solche Ergebnisse kommen beispielsweise von einer Likert-Skala, bei der die Werte 1-5 z.B. für “stimme gar nicht zu” bis “stimme voll zu” stehen.
Spearman-Rangkorrelation
Die Spearman-Rangkorrelation ist eine nicht-parametrische Version der Pearson-Korrelation, die auf Rängen statt auf den tatsächlichen Werten basiert. Sie ist daher weniger anfällig für Ausreißer und kann auch monotone, nicht-lineare Beziehungen erfassen.
Die Spearman-Korrelation sollte verwendet werden, wenn:
- Die Beziehung zwischen den Variablen monoton, aber nicht linear ist (wie bei
y5) - Die Daten ordinalskaliert sind (wie bei
y6) - Die Daten Ausreißer enthalten
- Die Daten nicht normalverteilt sind
Die Spearman-Rangkorrelation, oft als \(r_s\) bezeichnet, basiert auf dem Prinzip, zuerst die tatsächlichen Datenwerte in Ränge umzuwandeln und dann den Pearson-Korrelationskoeffizienten auf diese Ränge anzuwenden. Die Formel für den Spearman-Korrelationskoeffizienten lautet:
\[r_s = \frac{\sum_{i=1}^{n} (R(x_i) - \overline{R(x)})(R(y_i) - \overline{R(y)})}{\sqrt{\sum_{i=1}^{n} (R(x_i) - \overline{R(x)})^2 \sum_{i=1}^{n} (R(y_i) - \overline{R(y)})^2}}\]
Wobei:
- \(R(x_i)\) und \(R(y_i)\) die Ränge der Beobachtungen \(x_i\) und \(y_i\) sind
- \(\overline{R(x)}\) und \(\overline{R(y)}\) die Mittelwerte der Ränge sind
Wenn wir hier von Rängen sprechen, dann sind tatsächlich einfach die Positionen der Werte in einer sortierten Liste gemeint. So hätten die Werte 10.5, 13.1, 12, 9.8 die Ränge 2, 4, 3, 1. Wenn es zwei gleiche Werte gibt, dann erhalten sie auch den gleichen Rang, der dann der Durchschnitt der Ränge ist, die sie sonst eingenommen hätten. Ränge können z.B. mit scipy.stats.rankdata() berechnet werden.
Wir können die Spearman-Korrelation mit der Funktion stats.spearmanr() oder mit der Pandas-Methode .corr(method='spearman') berechnen. Hier wollen wir die Korrelationen mit beiden Methoden berechnen, obwohl die Pearson-Korrelation für y5 und y6 nicht geeignet ist:
# Variablen in einer Liste speichern
variables = [
('y1', y1, 'linear'),
('y5', y5, 'nichtlinear'),
('y6', y6, 'ordinal')
]
# Leere Listen für Ergebnisse
results_data = []
# Schleife über alle Variablen
for var_name, var_data, var_type in variables:
# Berechne beide Korrelationstypen
pearson_r, _ = stats.pearsonr(x, var_data)
spearman_r, _ = stats.spearmanr(x, var_data)
# Füge Ergebnisse zur Liste hinzu
results_data.append({
'Variable': f"{var_name} ({var_type})",
'Pearson r': round(pearson_r, 4),
'Spearman r': round(spearman_r, 4)
})
# Erstelle DataFrame aus den Ergebnissen
results = pd.DataFrame(results_data)
results Variable Pearson r Spearman r
0 y1 (linear) 0.8943 0.8843
1 y5 (nichtlinear) 0.8602 0.9884
2 y6 (ordinal) 0.9009 0.8994Die Ergebnisse zeigen:
- Für lineare Beziehungen (x-y1): Beide Methoden liefern ähnliche Werte. Bei Verwendung von Spearman in Fällen, in denen Pearson angebracht gewesen wäre, verliert man etwas an statistischer Power2, da die Rangbildung einen gewissen Informationsverlust bedeutet.
Für nichtlineare Beziehungen (x-y5): Hier sehen wir den größten Unterschied. Die Spearman-Korrelation ist deutlich höher als die Pearson-Korrelation. Der höhere Wert entspricht ja aber auch der tatsächlichen Beziehung zwischen den Variablen. Schaut man sich die Punkte an, so streuen sie sehr wenig, sondern folgen einem klaren Trend - nur eben keinem linearen. Dies zeigt die Stärke von Spearman: Der Zusammenhang wird erfasst - unabhängig der genauen Form der Beziehung.
Für ordinale Daten (x-y6): Beide Korrelationen sind ähnlich. Dies könnte überraschen, da man für ordinale Daten eigentlich einen Vorteil von Spearman erwarten würde. In diesem Fall liegen die Werte jedoch auf unserer 5-Punkt-Skala relativ gleichmäßig verteilt und approximieren daher eine lineare Beziehung ausreichend gut. In der Praxis kann das aber natürlich auch ganz anders aussehen.
Diese Ergebnisse unterstreichen die wichtige Faustregel: Wenn die Daten einen klaren monotonen, aber nicht-linearen Zusammenhang aufweisen, kann Spearman deutlich aussagekräftiger sein als Pearson. Bei linearen Beziehungen sind beide Methoden ähnlich effektiv, wobei Pearson bei normalverteilten Daten theoretisch etwas effizienter ist.
Weitere Korrelationsmethoden
Der Vollständigkeit halber sei erwähnt, dass es noch einige weitere Korrelationsmethoden gibt, die in speziellen Fällen nützlich sein können. Wir nenne hier aber lediglich ein paar und gehen hier nicht weiter auf sie ein:
-
Kendall’s Tau-Korrelation
- Verwenden Sie diese Methode für ordinale Daten und monotone Beziehungen, besonders bei kleineren Stichprobengrößen oder wenn die Daten Ausreißer enthalten. Sie ist robuster als die Spearman-Korrelation und eignet sich gut, wenn die Annahmen für die Pearson-Korrelation nicht erfüllt sind.
scipy.stats.kendalltau(x, y)- Wikipedia: Kendall rank correlation coefficient
-
Point-Biserial-Korrelation
- Ideal für Zusammenhänge zwischen kontinuierlichen und dichotomen Variablen (z.B. Geschlecht vs. Einkommen). Eine Spezialform der Pearson-Korrelation für binäre Zielvariablen.
scipy.stats.pointbiserialr(x, y)- Wikipedia: Point-biserial correlation
-
Distance-Korrelation
- Erkennt lineare UND nicht-lineare Zusammenhänge (0 bei Unabhängigkeit). Besonders nützlich für komplexe Datensätze mit nicht-monotonen Beziehungen.
scipy.spatial.distance.correlation(u, v)- Wikipedia: Distance correlation
Zusammenfassung
Korrelation misst die Stärke und Richtung des statistischen Zusammenhangs zwischen zwei Variablen. Der Pearson-Korrelationskoeffizient quantifiziert lineare Beziehungen und nimmt Werte zwischen -1 und 1 an, wobei Werte nahe ±1 starke Zusammenhänge anzeigen. Wichtig ist, dass Korrelation nicht automatisch Kausalität impliziert - ein fundamentales Konzept in der Datenanalyse. Für die Berechnung in Python stehen verschiedene Methoden zur Verfügung, darunter Funktionen in NumPy, Pandas und SciPy. Korrelationsmatrizen und deren Visualisierung als Heatmaps ermöglichen die gleichzeitige Darstellung vieler paarweiser Beziehungen. Bei z.B. nicht-linearen Beziehungen oder ordinalen Daten ist der Spearman-Rangkorrelationskoeffizient oft geeigneter, da er auf Rängen statt auf Absolutwerten basiert und so auch monotone, nicht-lineare Zusammenhänge erfassen kann. Die Wahl der richtigen Korrelationsmethode hängt von der Datenbeschaffenheit und der Fragestellung ab.
- Correlation Doesn’t Equal Causation: Crash Course Statistics #8
- Korrelation KANN Kausalität implizieren | Statistik Missverständnisse
- Covariance, Clearly Explained!!!
- Pearson’s Correlation, Clearly Explained!!!
- Kendall’s Tau Easily explained
- Point-biserial Correlation Simply explained
- Interpreting Correlations
- Guess the correlation
Übungen
Übung 1
Der “Datasaurus Dozen” ist ein Datensatz, der die Wichtigkeit der Datenvisualisierung und die Limitierungen von Korrelation demonstriert. Importiere die Daten von der angegebenen URL und führe folgende Schritte durch:
- Lade den Datensatz
- Erstelle einen Scatterplot pro Eintrag in der Spalte “dataset”
- Berechne die Korrelation zwischen x und y für jeden Eintrag in “dataset”
- Speichere die Korrelationen in einem DataFrame
Hinweis: Die Ergebnisse sind möglicherweise überraschend. Betrachte die Scatterplots und vergleiche sie mit den berechneten Korrelationen!
# Importiere die Daten
pfad = "https://raw.githubusercontent.com/SchmidtPaul/ExampleData/main/datasaurus_dozen/datasaurus_dozen.csv"Übung 2
Erstelle eine Korrelationsmatrix correlation_matrix_neu für einen DataFrame df_neu mit den Variablen x und y1-y6 aus dem Kapitel. Erstelle die Korrelationsmatrix manuell und nicht mit der .corr()-Methode. Verwende dabei für die Korrelationen mit y5 und/oder y6 die Spearman-Methode, und für alle anderen Korrelationen die Pearson-Methode.
Zeige die Matrix als Heatmap an und füge eine Anmerkung unter der Abbildung hinzu, die erklärt, welche Korrelationsmethode für welche Variablenpaare verwendet wurde, z.B. so:
fig.text(0.01, 0.01, 'hier der text', fontsize=10)
plt.subplots_adjust(bottom=0.15)Übung 3
Analysiere den Boston Housing Dataset, der wichtige Faktoren für Immobilienpreise in verschiedenen Vororten von Boston enthält. Führe folgende Schritte durch:
- Lade den Datensatz
- Erstelle eine Korrelationsmatrix für alle numerischen Variablen
- Visualisiere die Korrelationsmatrix als Heatmap
- Identifiziere die drei Variablen, die am stärksten mit dem Immobilienwert (MEDV) korrelieren
- Erstelle Scatterplots für diese drei Variablenpaare
Hinweis: Diese csv-Datei hat eine kleine Macke. Sowas kommt in der Praxis oft vor. Du solltest das Problem schnell bemerken, wenn du ihn einfach mit dem Code hierunter importierst. Um den Datensatz zu sehen, kannst du auch einfach der URL im Browser folgen und du wirst auch ohne scrollen die Macke sehen können. Jedenfalls kannst du mit einem einzigen zusätzlichen Argument in pd.read() das Problem umgehen.
# Importiere die Daten
pfad="https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/boston_housing/boston_house_prices.csv"
boston=pd.read(pfad)Variablenbeschreibung:
- CRIM: Kriminalitätsrate pro Kopf
- ZN: Anteil der Wohngrundstücke über 25.000 sq.ft.
- INDUS: Anteil der Nicht-Einzelhandelsflächen pro Stadt
- CHAS: Charles River Dummy-Variable (1 wenn Grundstück am Fluss liegt, sonst 0)
- NOX: Stickoxid-Konzentration
- RM: Durchschnittliche Anzahl der Räume pro Wohnung
- AGE: Anteil der Eigentumswohnungen, die vor 1940 gebaut wurden
- DIS: Gewichtete Entfernungen zu fünf Bostoner Beschäftigungszentren
- RAD: Index der Erreichbarkeit von Schnellstraßen
- TAX: Grundsteuersatz pro 10.000$
- PTRATIO: Schüler-Lehrer-Verhältnis
- B: 1000(Bk - 0.63)², wobei Bk der Anteil der Schwarzen pro Stadt ist
- LSTAT: Prozentsatz der Bevölkerung mit niedrigem Status
- MEDV: Mittlerer Wert der Eigenheime in 1000$
Hinweis: Lösungen zu den meisten Übungsaufgaben findet ihr, indem ihr ganz oben rechts im Kapitel auf den </> Code Button klickt und dann entsprechend nach ganz unten scrollt. Es ist Absicht, dass dies etwas umständlich ist.
Fußnoten
Im Gegensatz zu beispielsweise einer einfachen linearen Regression, welche wir in einem späteren Kapitel behandeln.↩︎
Statistische Power (auch: Güte, Macht, Trennschärfe) ist ein Konzept, dass eng mit p-Werte und statistischer Signifikanz zusammenhängt, sodass auch hier wieder für den Moment auf ein folgendes Kapitel verwiesen wird. Sie gibt die Fähigkeit eines Tests an, Unterschiede (Effekte) zu erkennen, wenn sie in Wirklichkeit vorhanden sind.↩︎