import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split, cross_val_score, RepeatedStratifiedKFold
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler
np.random.seed(42)Support Vector Machines
Als letzte Klassifikationsmethode in diesem Kurs schauen wir uns nun Support Vector Machines (SVM) an. Wie kNN verfolgt auch SVM einen geometrischen Ansatz – beide Methoden arbeiten mit Distanzen und räumlichen Beziehungen zwischen Datenpunkten. Während kNN jedoch Entscheidungen auf Basis der nächsten Nachbarn trifft, sucht SVM die (Position der) optimale(n) Trennebene zwischen verschiedenen Klassen. Aber was macht eine Trennlinie “optimal”?
Einfaches Beispiel: Eindimensionale Trennung
Beginnen wir mit dem einfachsten Fall: der Trennung einer binären Klasse (= zweier Pinguinarten) anhand nur eines metrischen Features (= body_mass_g). Wir konzentrieren uns wie so oft auf die Gruppen Adelie und Gentoo, erstellen aber zunächst ein “idealisiertes” Beispiel, bei dem die Gruppen klar getrennt sind.
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
# Fokus auf Adelie vs. Gentoo (die sind am besten trennbar)
penguins_filtered = penguins[penguins['species'].isin(['Adelie', 'Gentoo'])].copy()
penguins_filtered = penguins_filtered.dropna(subset=['body_mass_g'])
# Für die Demonstration: entferne Punkte im Grenzbereich für perfekte Trennung
adelie_clean = penguins_filtered[
(penguins_filtered['species'] == 'Adelie') &
(penguins_filtered['body_mass_g'] <= 3900)
]['body_mass_g']
gentoo_clean = penguins_filtered[
(penguins_filtered['species'] == 'Gentoo') &
(penguins_filtered['body_mass_g'] >= 4300)
]['body_mass_g']
print(f"Gefilterte Adelie: {adelie_clean.min():.0f} - {adelie_clean.max():.0f}g (n={len(adelie_clean)})")
print(f"Gefilterte Gentoo: {gentoo_clean.min():.0f} - {gentoo_clean.max():.0f}g (n={len(gentoo_clean)})")
print(f"Keine Überlappung! Gap: {gentoo_clean.min() - adelie_clean.max():.0f}g")Gefilterte Adelie: 2850 - 3900g (n=106)
Gefilterte Gentoo: 4300 - 6300g (n=117)
Keine Überlappung! Gap: 400gJetzt visualisieren wir diese eindimensionale Trennung:
Code zeigen/verstecken
# Eindimensionale Datenvisualisierung - alle Punkte auf y=0
fig, ax = plt.subplots(figsize=(12, 6), layout='tight')
# Alle Punkte auf y=0 platzieren
ax.scatter(adelie_clean, np.zeros(len(adelie_clean)), alpha=0.7, s=60,
color=colors['Adelie'], label='Adelie (gefiltert)', edgecolor='black', linewidth=0.5)
ax.scatter(gentoo_clean, np.zeros(len(gentoo_clean)), alpha=0.7, s=60,
color=colors['Gentoo'], label='Gentoo (gefiltert)', edgecolor='black', linewidth=0.5)
# Optimale Trennlinie: Mitte zwischen den Gruppen
trennpunkt = (adelie_clean.max() + gentoo_clean.min()) / 2
ax.axvline(trennpunkt, color='red', linestyle='-', linewidth=3,
label=f'Optimale Trennung ({trennpunkt:.0f}g)')
# Margin visualisieren
margin_links = adelie_clean.max() # Nächster Adelie-Punkt
margin_rechts = gentoo_clean.min() # Nächster Gentoo-Punkt
ax.axvline(margin_links, color='red', linestyle='--', alpha=0.7, linewidth=2)
ax.axvline(margin_rechts, color='red', linestyle='--', alpha=0.7, linewidth=2)
ax.axvspan(margin_links, margin_rechts, alpha=0.2, color='yellow',
label=f'Margin ({margin_rechts - margin_links:.0f}g)')
# Support Vectors hervorheben
ax.scatter([margin_links], [0], s=300, facecolors='none',
edgecolors=colors['Adelie'], linewidth=4, label='Support Vector')
ax.scatter([margin_rechts], [0], s=300, facecolors='none',
edgecolors=colors['Gentoo'], linewidth=4)
ax.set_xlabel('Körpergewicht (g)');
ax.set_ylabel('');
ax.set_title('1D SVM: Perfekte Trennung mit maximaler Margin');
ax.legend();
ax.grid(True, alpha=0.3);
ax.set_ylim(-0.3, 0.3);
ax.set_yticks([]);
plt.show()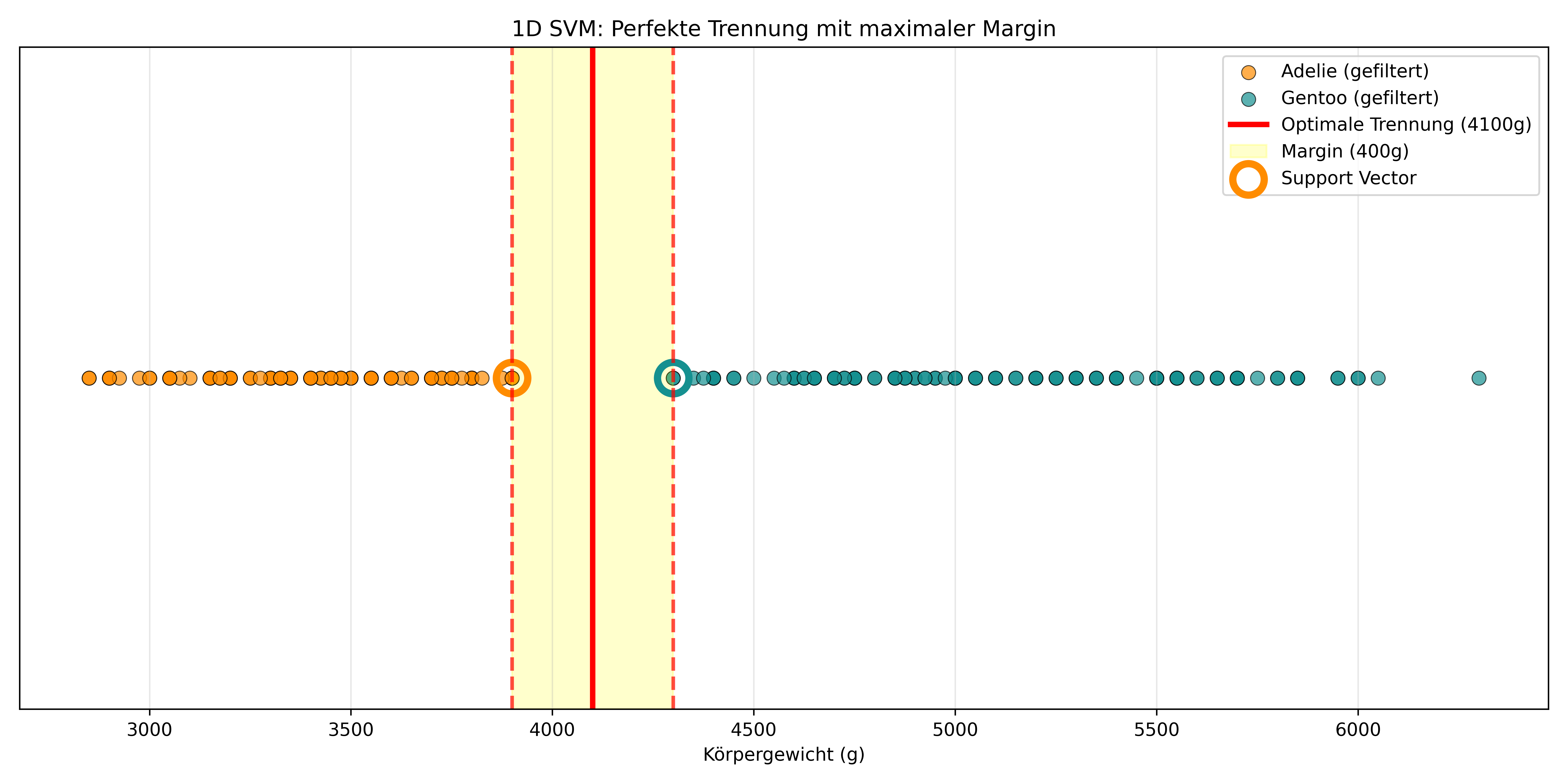
In dieser Visualisierung sehen wir bereits die Trenngrenze (rote Linie), die Margin (gelber Bereich) und die Support Vectors (umkreist) – Konzepte, die wir jetzt Schritt für Schritt erklären werden.
Das ist der Kern von SVM: Die Methode sucht die beste Trennlinie zwischen den Gruppen, sodass die Margin maximiert wird. Die Margin ist der Abstand zwischen der Trennlinie und den nächstgelegenen Punkten beider Klassen. In unserem gefilterten eindimensionalen Beispiel ist die Margin durch den größten Wert der Adelie-Gruppe (3900g) und den kleinsten Wert der Gentoo-Gruppe (4300g) vorgegeben. Die optimale Trenngrenze liegt dann genau in der Mitte bei 4100g.
In diesem idealisierten Beispiel ging das jetzt so einfach, dass es sich gar nicht wie ein Machine Learning Algorithmus anfühlt. Wir tasten uns nun aber an komplexere Fälle, sodass klarer wird, dass es nicht immer so simpel ist.
Wir können allerdings jetzt schon klären, warum es “Support Vector Machine” heißt: Der Name kommt daher, dass nur wenige spezielle Datenpunkte – die Support Vectors – die Position der Trennlinie bestimmen. In unserem idealisierten Beispiel sind das genau die beiden Randpunkte: der schwerste Adelie-Pinguin (3900g) und der leichteste Gentoo-Pinguin (4300g).
Auch wenn wir 1000 weitere Datenpunkte hinzufügen würden, solange sie nicht näher an die Trennlinie herankommen als unsere aktuellen Support Vectors, ändert sich die optimale Trennlinie nicht! SVM ist also robust gegenüber “irrelevanten” Datenpunkten – nur die Grenzfälle bestimmen die Entscheidungsgrenze.
In Szenarien mit mehr als einem Feature sind es dann eben Vektoren und nicht Punkte, da sie ja z.B. nicht nur das Körpergewicht, sondern eben Werte aller übergebenen Feature enthalten.
Der C-Parameter: Fehlertoleranz einführen
In der Realität gibt es natürlich selten so perfekt trennbare Daten wie oben. Und sobald wir die nicht-idealisierte Version unserer Pinguin-Körpergewichte betrachten, überlappen diese ja auch. Aber: wenn Gruppen überlappen, gibt es keine perfekte Trenngrenze in der Mitte und auch welche Werte eigentlich die Support Vektoren sind ist nicht ohne Weiteres klar. Um trotzdem eine Trennlinie finden zu können, müssen wir den Kompromiss eingehen und Fehlklassifikationen zulassen. So sind wir also selbst in diesem eindimensionalen Raum schon in einer etwas kniffligeren Situation bei der ein Kompromiss bei der Optimierung getroffen werden muss.
Schauen wir uns an, was passiert, wenn wir alle Daten verwenden – also auch die überlappenden:
# Alle Daten anzeigen - mit Überlappung
all_adelie = penguins_filtered[penguins_filtered['species'] == 'Adelie']['body_mass_g']
all_gentoo = penguins_filtered[penguins_filtered['species'] == 'Gentoo']['body_mass_g']
print(f"Alle Adelie: {all_adelie.min():.0f} - {all_adelie.max():.0f}g (n={len(all_adelie)})")
print(f"Alle Gentoo: {all_gentoo.min():.0f} - {all_gentoo.max():.0f}g (n={len(all_gentoo)})")
overlap_start = max(all_adelie.min(), all_gentoo.min())
overlap_end = min(all_adelie.max(), all_gentoo.max())
print(f"Überlappung: {overlap_start:.0f} - {overlap_end:.0f}g")Alle Adelie: 2850 - 4775g (n=151)
Alle Gentoo: 3950 - 6300g (n=123)
Überlappung: 3950 - 4775gDer C-Parameter (standardmäßig auf 1.0 gesetzt) kontrolliert den Kompromiss zwischen:
- Große Margin (weite Trennlinie, weniger Overfitting)
- Weniger Fehlklassifikationen (engere Trennlinie, mehr Anpassung an Trainingsdaten)
Code zeigen/verstecken
# Demonstration des C-Parameters mit realen überlappenden Daten
X_1d = penguins_filtered[['body_mass_g']].values
y_1d = (penguins_filtered['species'] == 'Gentoo').astype(int).values
# SVM mit verschiedenen C-Werten trainieren
c_values = [0.1, 10.0]
fig, axes = plt.subplots(2, 1, figsize=(15, 8), layout='tight')
for i, C in enumerate(c_values):
svm = SVC(kernel='linear', C=C, random_state=42);
svm.fit(X_1d, y_1d);
# Entscheidungsgrenze (in 1D ist das ein Punkt)
decision_boundary = -svm.intercept_[0] / svm.coef_[0][0]
# Support Vectors finden (in ursprünglichen Einheiten)
support_indices = svm.support_
support_vectors = X_1d[support_indices].flatten()
# Plot erstellen
ax = axes[i]
adelie_mask = y_1d == 0
gentoo_mask = y_1d == 1
ax.scatter(X_1d[adelie_mask], np.zeros(np.sum(adelie_mask)),
alpha=0.6, color=colors['Adelie'], s=40, label='Adelie');
ax.scatter(X_1d[gentoo_mask], np.zeros(np.sum(gentoo_mask)),
alpha=0.6, color=colors['Gentoo'], s=40, label='Gentoo');
# Support Vectors hervorheben
ax.scatter(support_vectors, np.zeros(len(support_vectors)),
s=200, facecolors='none', edgecolors='red', linewidth=3,
label='Support Vectors');
# Entscheidungsgrenze
ax.axvline(decision_boundary, color='red', linestyle='-', linewidth=3,
label=f'Grenze ({decision_boundary:.0f}g)');
ax.set_xlabel('Körpergewicht (g)');
ax.set_title(f'C = {C}\n{len(support_vectors)} Support Vectors');
ax.legend();
ax.grid(True, alpha=0.3);
ax.set_ylim(-0.1, 0.1);
ax.set_yticks([]);
plt.show()
- Kleines C (C=0.1): Mehr Fehlertoleranz, größerer Margin, mehr Support Vectors
- Großes C (C=10): Weniger Fehlertoleranz, kleinerer Margin, weniger Support Vectors
SVM optimiert also nicht nur eine Trenngrenze mit maximaler Margin, sondern findet gleichzeitig den optimalen Kompromiss zwischen Margin-Größe und der Anzahl der nötigen Fehlklassifikationen.
Wie funktioniert die Optimierung?
Ein interessanter Aspekt von SVM ist, dass der Optimierungsprozess nicht iterativ funktioniert. SVM löst ein quadratisches Optimierungsproblem mit einer mathematisch eindeutigen Lösung.
Konkret minimiert SVM diese Zielfunktion:
\(\text{Minimiere: } \frac{1}{2}||w||^2 + C \sum_{i=1}^n \xi_i\)
Diese Formel zeigt den Kompromiss deutlich – sie besteht aus zwei Komponenten:
- \(\frac{1}{2}||w||^2\): Margin-Maximierung (kleinerer Wert bedeutet größerer Margin)
- \(C \sum_{i=1}^n \xi_i\): Fehlklassifikations-Minimierung (ξᵢ sind die “Slack-Variablen” für Fehlklassifikationen)
Der C-Parameter gewichtet direkt zwischen diesen beiden Zielen: Ein großes C legt mehr Gewicht auf die Fehlklassifikations-Vermeidung, ein kleines C bevorzugt einen größeren Margin.
Das bedeutet konkret: SVM “probiert” nicht verschiedene Kombinationen von Support Vectors aus, um die beste zu finden. Stattdessen ergibt sich aus der mathematischen Lösung automatisch, welche Punkte Support Vectors werden und welche nicht. Dies geschieht durch die sogenannten Karush-Kuhn-Tucker (KKT) Bedingungen, die bestimmen:
- Punkte weit von der Grenze: Sind irrelevant für die Lösung (keine Support Vectors)
-
Punkte auf der Margin: Werden automatisch zu Support Vectors
- Punkte innerhalb der Margin: Werden ebenfalls zu Support Vectors (oft fehlklassifiziert)
Deshalb sehen wir im überlappenden Fall plötzlich mehr Support Vectors als im perfekt trennbaren Fall – es ist eine direkte Konsequenz der mathematischen Optimierung, nicht eine Designentscheidung des Algorithmus.
Erweiterung auf höhere Dimensionen
Wie auch schon in vorigen Kapiteln, lässt sich das Konzept elegant auf höhere Dimensionen übertragen:
- In 1D suchen wir einen Trennpunkt,
- in 2D eine Trennlinie,
- in 3D eine Trennebene und
- in höheren Dimensionen eine Hyperebene.
Das mathematische Prinzip der Margin-Maximierung und gleichzeitiger Berücksichtigung der Fehlklassifikationen bleibt dabei gleich.
Aber: Sobald wir mit mehr als einem Feature arbeiten, wird Feature Scaling kritisch wichtig! Genau wie bei k-Nearest Neighbors beruht SVM auf Distanzberechnungen zwischen Datenpunkten. Wenn ein Feature (z.B. Körpergewicht in Gramm) viel größere Werte hat als ein anderes (z.B. Flossenlänge in Millimetern), dominiert es die gesamte Optimierung.
Im eindimensionalen Beispiel oben war Scaling noch nicht nötig – wir hatten nur ein Feature in seiner natürlichen Skalierung. Aber jetzt, wo wir zu höheren Dimensionen übergehen, müssen wir standardisieren, damit alle Features fair zur Margin-Berechnung beitragen können.
SVM in 2D: Das bekannte Pinguin-Beispiel
Wir können uns nun also SVM mit unserem bewährten zweidimensionalen Pinguin-Beispiel und der bewährten plot_classifier() Funktion anschauen:
Code zeigen/verstecken
# Daten vorbereiten wie in den vorangegangenen Kapiteln
penguins_binary = penguins[penguins['species'].isin(['Adelie', 'Gentoo'])].copy()
penguins_binary = penguins_binary.dropna(subset=['body_mass_g', 'flipper_length_mm'])
# Binäre Zielvariable erstellen (0 = Adelie, 1 = Gentoo)
penguins_binary['species_binary'] = (penguins_binary['species'] == 'Gentoo').astype(int)
# Features und Ziel definieren
X = penguins_binary[["body_mass_g", "flipper_length_mm"]].values
y = penguins_binary["species_binary"].values
# Train-Test Split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
print(f"Trainingsdaten: {len(X_train)} Pinguine")
print(f"Testdaten: {len(X_test)} Pinguine")
#####
def plot_classifier(model, X_train, y_train, X_test, y_test,
proba=False, xlabel=None, ylabel=None, title=None,
class_colors=None, figsize=(12, 5), axes=None):
"""
Visualisiert Klassifikationsgrenzen für ein trainiertes Modell
Parameter:
- model: Trainiertes sklearn Klassifikationsmodell
- X_train, y_train: Trainingsdaten (Features und Labels)
- X_test, y_test: Testdaten (Features und Labels)
- proba: Bool, ob Wahrscheinlichkeiten (True) oder Klassen (False) gezeigt werden
- xlabel, ylabel: Achsenbeschriftungen
- title: Titel der Abbildung
- class_colors: Dictionary mit Farben für die Klassen {0: 'farbe1', 1: 'farbe2'}
- figsize: Größe der Abbildung als Tuple (width, height)
- axes: Optionales Tupel oder Liste mit zwei matplotlib-Achsenobjekten – wenn angegeben, wird in diese gezeichnet
"""
# Subplot-Layout erstellen: 1 Zeile, 2 Spalten (nur falls keine Achsen übergeben wurden)
if axes is None:
fig, axes = plt.subplots(1, 2, figsize=figsize, sharex=True, sharey=True, layout='tight')
own_fig = True
else:
own_fig = False
# Standard-Farben (Rot & Blau) verwenden, falls keine angegeben
if class_colors is None:
class_colors = {0: 'red', 1: 'blue'}
# Custom Colormap für den Hintergrund erstellen
# Von Klasse 0 (z.B. orange) über weiß zu Klasse 1 (z.B. türkis)
gradient_colors = [class_colors[0], 'white', class_colors[1]]
custom_cmap = LinearSegmentedColormap.from_list("CustomDiverging", gradient_colors, N=256)
# Gemeinsame Grenzen für beide Plots berechnen
# Alle Daten (Training + Test) kombinieren um einheitliche Achsen zu haben
X_all = np.vstack([X_train, X_test])
x_margin = (X_all[:, 0].max() - X_all[:, 0].min()) * 0.05 # 5% Rand
y_margin = (X_all[:, 1].max() - X_all[:, 1].min()) * 0.05 # 5% Rand
x_min = X_all[:, 0].min() - x_margin
x_max = X_all[:, 0].max() + x_margin
y_min = X_all[:, 1].min() - y_margin
y_max = X_all[:, 1].max() + y_margin
# Meshgrid für Hintergrund-Vorhersagen erstellen
# 1000x1000 Grid für glatte Darstellung
xx, yy = np.meshgrid(
np.linspace(x_min, x_max, 1000),
np.linspace(y_min, y_max, 1000)
)
# Vorhersagen für jeden Punkt im Grid
if proba:
# Wahrscheinlichkeiten für Klasse 1
zz = model.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1].reshape(xx.shape)
else:
# Klassenlabels (0 oder 1)
zz = model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
# Beide Subplots (Training und Test) erstellen
for ax, X, y, subset in zip(axes, [X_train, X_test], [y_train, y_test],
["Trainingsdaten", "Testdaten"]):
# Vorhersagen für die aktuellen Daten
y_pred = model.predict(X)
# Hintergrund mit Klassifikationsgrenzen zeichnen
if proba:
# Kontinuierliche Wahrscheinlichkeiten als Heatmap
ax.imshow(zz, origin="lower", aspect="auto",
extent=(x_min, x_max, y_min, y_max),
vmin=0, vmax=1, alpha=0.25, cmap=custom_cmap);
else:
# Diskrete Klassengrenzen
ax.contourf(xx, yy, zz,
alpha=0.25,
vmin=0, vmax=1,
levels=[-0.5, 0.5, 1.5], # Grenzen für Klasse 0 und 1
colors=[class_colors[0], class_colors[1]]);
# Datenpunkte zeichnen
# Gesichtsfarbe basiert auf wahrer Klasse
face_colors = [class_colors[int(label)] for label in y]
# Randfarbe zeigt richtige (schwarz) vs. falsche (rot) Vorhersagen
edge_colors = ['black' if true_label == pred_label else 'red'
for true_label, pred_label in zip(y, y_pred)]
ax.scatter(X[:, 0], X[:, 1],
c=face_colors,
edgecolor=edge_colors,
linewidth=1,
s=50);
# Subplot-Eigenschaften setzen
ax.set_title(subset);
ax.set_xlim(x_min, x_max);
ax.set_ylim(y_min, y_max);
if xlabel:
ax.set_xlabel(xlabel);
if ylabel:
ax.set_ylabel(ylabel);
# Gesamttitel und Anzeige nur, wenn eigene Figure erzeugt wurde
if own_fig:
if title:
fig.suptitle(title, fontsize=14);
plt.show()Trainingsdaten: 205 Pinguine
Testdaten: 69 PinguineNun trainieren wir unser SVM. Da wir jetzt zwei Features haben, ist die Standardisierung unerlässlich:
# Standardisierung (wichtig für SVM!)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
print("Feature-Bereiche nach Standardisierung:")
print(f" Feature 1: {X_train_scaled[:, 0].min():.2f} bis {X_train_scaled[:, 0].max():.2f}")
print(f" Feature 2: {X_train_scaled[:, 1].min():.2f} bis {X_train_scaled[:, 1].max():.2f}")
# Linearen SVM trainieren
svm_linear = SVC(kernel='linear', random_state=42)
svm_linear.fit(X_train_scaled, y_train);
# Performance bewerten
train_accuracy = svm_linear.score(X_train_scaled, y_train)
test_accuracy = svm_linear.score(X_test_scaled, y_test)
print(f"\nLinearer SVM Performance:")
print(f" Training Accuracy: {train_accuracy:.3f}")
print(f" Test Accuracy: {test_accuracy:.3f}")
# Visualisierung mit skalierten Daten
# (Die Achsenwerte sind jetzt standardisiert, d.h. Mittelwert=0, Standardabweichung=1)
plot_classifier(svm_linear, X_train_scaled, y_train, X_test_scaled, y_test,
proba=False,
xlabel='Körpergewicht (standardisiert)',
ylabel='Flossenlänge (standardisiert)',
title='Linearer SVM: Adelie vs Gentoo',
class_colors={0: colors['Adelie'], 1: colors['Gentoo']})Feature-Bereiche nach Standardisierung:
Feature 1: -1.77 bis 2.39
Feature 2: -2.03 bis 1.91
Linearer SVM Performance:
Training Accuracy: 0.980
Test Accuracy: 1.000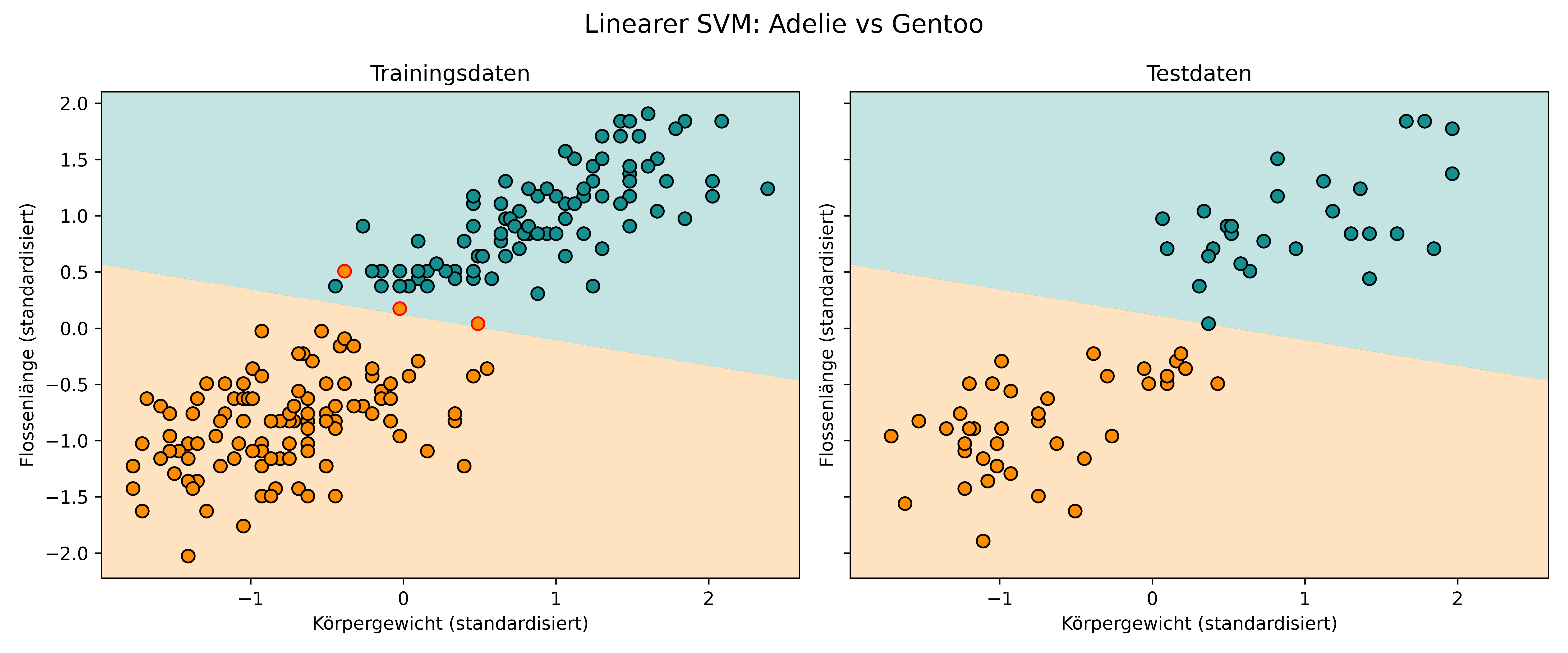
Wir sehen, dass der unser SVM hier - wie die logistische Regression - eine gerade Linie durch den zweidimensionalen Raum legt. Dies ist die optimale lineare Trenngrenze mit gleichzeitig maximaler Margin zwischen den beiden Klassen und möglichst wenig Fehlklassifikationen.
Man könnte also meinen, dass wir nun mit dem Kapitel fertig sind. Tatsächlich haben wir uns aber bis jetzt nur auf eine Art von SVM fokussiert: Die mit einem linearen Kernel - was man auch daran erkennt, dass wir SVC(kernel='linear') geschrieben haben.
SVM kann mehr: Nicht-lineare Klassifikationsgrenzen
Tatsächlich kann SVM nicht nur lineare Klassifikationsgrenzen erstellen, sondern auch komplexere Kurven usw. Das funktioniert, indem andere Kernel zugrunde gelegt werden. Schauen wir uns an, was passiert, wenn wir einen Polynomial-Kernel verwenden:
# Polynomial SVM trainieren (Grad 2)
svm_poly = SVC(kernel='poly', degree=2, random_state=42)
svm_poly.fit(X_train_scaled, y_train);
# Visualisierung mit skalierten Daten
plot_classifier(svm_poly, X_train_scaled, y_train, X_test_scaled, y_test,
proba=False,
xlabel='Körpergewicht (standardisiert)',
ylabel='Flossenlänge (standardisiert)',
title='Polynomial SVM (Grad 2): Adelie vs Gentoo',
class_colors={0: colors['Adelie'], 1: colors['Gentoo']})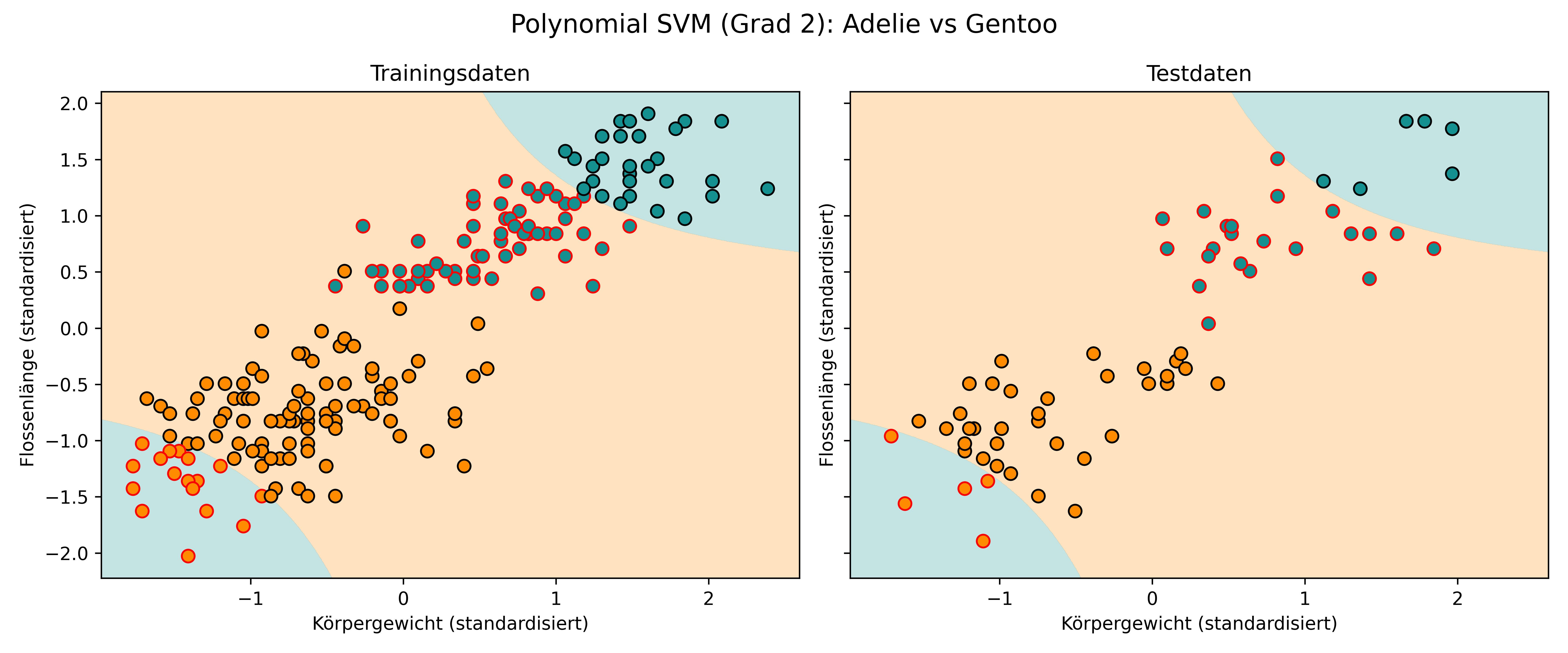
Plötzlich sehen wir zwei gekrümmte Entscheidungsgrenzen anstatt einer geraden Linie. Der Polynomial-Kernel ermöglicht es SVM, komplexere, nicht-lineare Muster in den Daten zu erkennen. Tatsächlich funktioniert diese Trennung hier nicht besonders gut, wie man sieht. Viel wichtiger ist aber: Wie ist das möglich und was sind Kernels?
Von linearer Trennung zu nicht-linearer Trennung
Bisher haben wir wie gesagt nur lineare SVM betrachtet. Aber natürlich sind Daten nicht immer linear trennbar. In solchen Fällen können wir zu nicht-linearen Trennmethoden übergehen.
Polynomial Transformationen
Eine Möglichkeit, nicht-lineare Trennmethoden zu erstellen, ist die Transformation der Daten in einen höherdimensionalen Raum. Leider gibt es in unserem Palmer Penguins Datensatz kein besonders gutes Beispiel für dieses Konzept, aber natürlich könnten Daten auch mal so verteilt sein, dass eine Art sowohl die kleinsten als auch die größten Werte eines Features hat, aber eben nicht die mittleren Werte. Damit wären wir noch immer im eindimensionalen Raum (also mit einem einzigen numerischen Feature), aber wir können ja solche Daten mal simulieren und das sähe dann so aus:
# 10 Pinguine mit gleichmäßig verteilten Gewichten
n_penguins = 10
weights = np.linspace(-2, 2, n_penguins) # Gleichmäßig verteilt von -2 bis 2
# Labels zuweisen: mittlere 4 → Klasse 0 (Adelie), äußere 6 → Klasse 1 (Gentoo)
labels = np.array([1, 1, 1, 0, 0, 0, 0, 1, 1, 1]) # U-förmiges MusterCode zeigen/verstecken
# Daten vorbereiten
X_sim = weights.reshape(-1, 1)
y_sim = labels
# Standardisierung
scaler_sim = StandardScaler()
X_sim_scaled = scaler_sim.fit_transform(X_sim)
# Visualisierung der 1D Daten
fig, ax = plt.subplots(figsize=(12, 5), layout='tight')
# 1D Visualisierung - alle Punkte auf y=0
ax.scatter(X_sim_scaled[y_sim==0], np.zeros(np.sum(y_sim==0)),
alpha=0.8, s=120, color=colors['Adelie'], label='Klasse 0 (mittlere)',
edgecolor='black', linewidth=1)
ax.scatter(X_sim_scaled[y_sim==1], np.zeros(np.sum(y_sim==1)),
alpha=0.8, s=120, color=colors['Gentoo'], label='Klasse 1 (äußere)',
edgecolor='black', linewidth=1)
ax.set_xlabel('Gewicht (standardisiert)');
ax.set_ylabel('');
ax.set_title('1D: Simulierte Daten');
ax.legend();
ax.grid(True, alpha=0.3);
ax.set_ylim(-0.4, 0.4);
ax.set_yticks([]);
plt.show()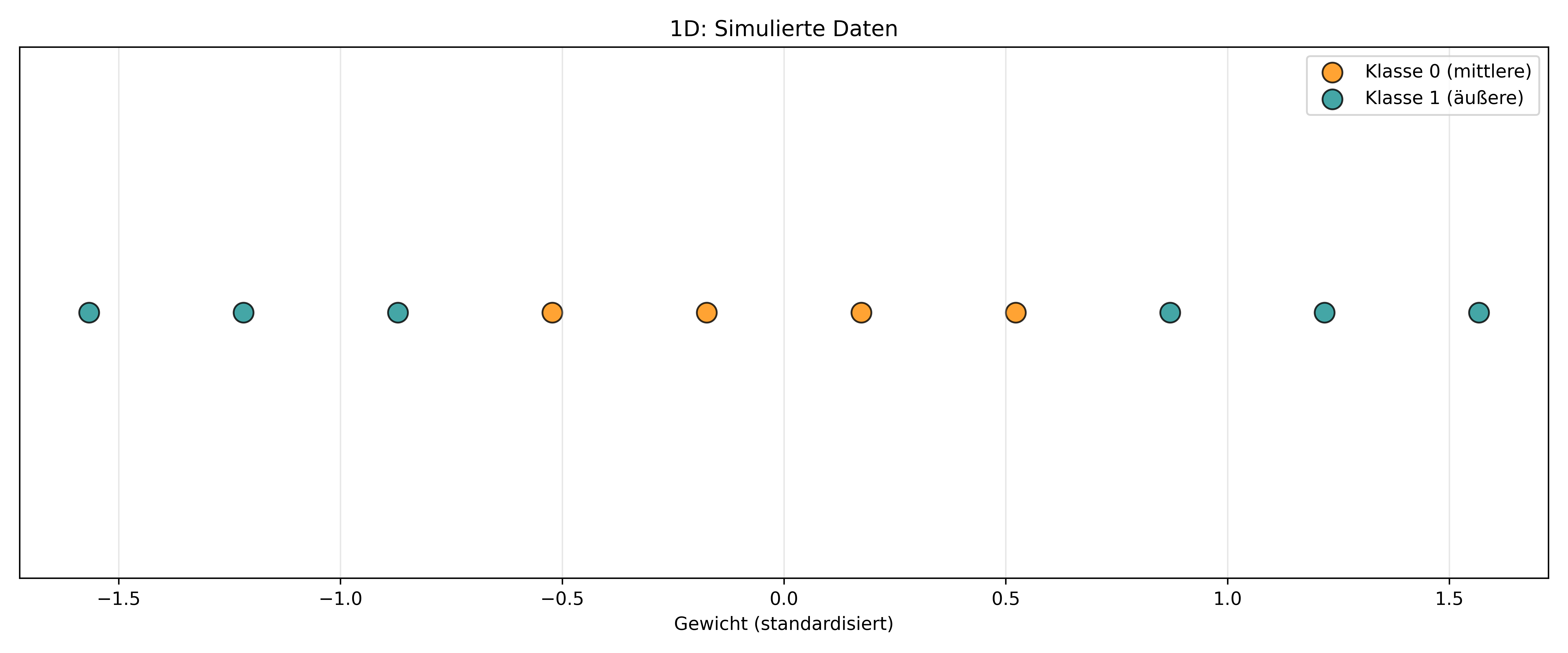
Man sieht sofort: Solche Daten kann man natürlich nicht wirklich mit einer einzigen Trenngeraden (genauer: einem Trennpunkt) trennen. Es gibt schlichtweg keinen einzelnen x-Wert, bei dem links nur die eine Klasse und rechts nur die andere Klasse steht.
Hier könnte man aber den Trick anwenden, der beim Polynomial Kernel verwendet wird: Prinzipiell werden die Daten so transformiert, dass sie eine zweite Dimension erhalten, die aber eben nur die transformierte erste Dimension ist - also hier alles quadriert. Zum Beispiel wird aus einem 1D-Feature x der 2D-Raum [x, x²]. Für speziell dieses simulierte Datenbeispiel wird offensichtlich, dass genau das tatsächlich hilft, um die Trennung durchzuführen:
# SVM Modell trainieren
svm_poly_sim = SVC(kernel='poly', degree=2, C=1000, random_state=42)
svm_poly_sim.fit(X_sim_scaled, y_sim);Code zeigen/verstecken
# Performance berechnen
poly_accuracy = svm_poly_sim.score(X_sim_scaled, y_sim)
# Visualisierung der Polynomial-Transformation
fig, axes = plt.subplots(1, 2, figsize=(15, 6), layout='tight')
# Plot 1: Original 1D Daten mit tatsächlichen Entscheidungsgrenzen
ax1 = axes[0]
# 1D Visualisierung
ax1.scatter(X_sim_scaled[y_sim==0], np.zeros(np.sum(y_sim==0)),
alpha=0.8, s=120, color=colors['Adelie'], label='Klasse 0 (mittlere)',
edgecolor='black', linewidth=1)
ax1.scatter(X_sim_scaled[y_sim==1], np.zeros(np.sum(y_sim==1)),
alpha=0.8, s=120, color=colors['Gentoo'], label='Klasse 1 (äußere)',
edgecolor='black', linewidth=1)
# Tatsächliche Entscheidungsgrenzen berechnen
x_range = np.linspace(X_sim_scaled.min()-0.5, X_sim_scaled.max()+0.5, 1000)
x_range_2d = x_range.reshape(-1, 1)
# Polynomial SVM Entscheidungsgrenze
poly_decisions = svm_poly_sim.decision_function(x_range_2d)
poly_boundary_indices = np.where(np.diff(np.sign(poly_decisions)))[0]
if len(poly_boundary_indices) > 0:
for idx in poly_boundary_indices:
ax1.axvline(x_range[idx], color='red', linestyle='-', linewidth=3, alpha=0.8)
ax1.axvline(x_range[poly_boundary_indices[0]], color='red', linestyle='-',
linewidth=3, label=f'Polynomial SVM ({len(poly_boundary_indices)} Grenzen)', alpha=0.8)
ax1.set_xlabel('Gewicht (standardisiert)');
ax1.set_ylabel('');
ax1.set_title('1D: Original Feature\nU-förmiges Muster → Linear unmöglich!');
ax1.legend();
ax1.grid(True, alpha=0.3);
ax1.set_ylim(-0.4, 0.4);
ax1.set_yticks([]);
# Plot 2: Nach Polynomial-Transformation (x, x²)
ax2 = axes[1]
# Transformierte Features: [x, x²]
X_transformed = X_sim_scaled.flatten() # x-Werte
X_squared = X_transformed**2 # x²-Werte
ax2.scatter(X_transformed[y_sim==0], X_squared[y_sim==0],
alpha=0.8, s=120, color=colors['Adelie'], label='Klasse 0 (transformiert)',
edgecolor='black', linewidth=1)
ax2.scatter(X_transformed[y_sim==1], X_squared[y_sim==1],
alpha=0.8, s=120, color=colors['Gentoo'], label='Klasse 1 (transformiert)',
edgecolor='black', linewidth=1)
# Echte Entscheidungsgrenze im transformierten Raum
x_fine = np.linspace(X_transformed.min()-0.5, X_transformed.max()+0.5, 500)
poly_decisions_fine = svm_poly_sim.decision_function(x_fine.reshape(-1, 1))
# Finde Nullstellen (Entscheidungsgrenzen)
decision_curve_x = []
decision_curve_x2 = []
tolerance = 0.02
for x_val in x_fine:
decision_val = svm_poly_sim.decision_function([[x_val]])[0]
if abs(decision_val) < tolerance:
decision_curve_x.append(x_val)
decision_curve_x2.append(x_val**2)
if len(decision_curve_x) > 1:
ax2.plot(decision_curve_x, decision_curve_x2, 'r-', linewidth=4, alpha=0.9,
label='Polynomial SVM Grenze', zorder=10)
ax2.set_xlabel('Gewicht (standardisiert)')
ax2.set_ylabel('Gewicht² (transformiert)')
ax2.set_title('2D: Nach Polynomial-Transformation\nLineare Trennung jetzt möglich!')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.suptitle('Polynomial SVM: Transformation macht lineare Trennung möglich',
fontsize=14)
plt.show()
Im rechten Plot sehen wir den nun zweidimensionalen Raum, weil auf der x-Achse weiterhin das Gewicht, aber auf der y-Achse nun auch noch das quadrierte Gewicht abgetragen ist. Nun ist es tatsächlich möglich eine Trenngerade, wie im Bild in rot dargestellt, durch die Punkt zu legen und die Klassen perfekt zu trennen. Links ist dann das Resultat - also die Trenngrenzen - wieder im eindimensionalen Raum dargestellt, wobei dort eigentlich mal wieder nur zwei Trennpunkte und nicht Trenngeraden zu sehen sein sollten.
Anhand dieses Beispiels wird klar, dass man also durch solche Transformationen doch funktionierende Trennungen schaffen - durch quasi “Pseudo-Dimensionen”. Das ursprünglich eindimensionale Problem wird zu einem zweidimensionalen Problem, in dem eine einfache horizontale Linie (im transformierten Raum) zur Trennung ausreicht.
Und dann gibt es eben nicht nur den Polynomial Kernel zweiten Grades. Polynomial Kernel können beliebige Grade haben (3, 4, 5, …), und es gibt auch ganz andere Kernel-Funktionen. Der RBF (Radial Basis Function) Kernel, den wir gleich kennenlernen werden, ist sogar noch flexibler und kann beliebig komplexe, nicht-lineare Entscheidungsgrenzen erstellen.
Der Kernel-Trick
Aber unabhängig davon ob linear, polynomial, RBF usw. kommt hier der eigentliche Clou des SVM Algorithmus, der als Kernel-Trick bezeichnet wird. Das Geniale hinter den Kulissen ist, dass die Transformation in der Praxis nie explizit durchgeführt wird. SVM berechnet nur die Skalarprodukte zwischen Datenpunkten, und diese können direkt im höherdimensionalen Raum berechnet werden, ohne die transformierten Features jemals zu erstellen.
Schauen wir uns das konkret für den Polynomial-Kernel 2. Grades an. Nehmen wir zwei Pinguine mit den Merkmalen P1 = (Körpergewicht, Schnabellänge) und P2 = (Körpergewicht, Schnabellänge) im ursprünglichen 2D-Raum:
Naiver Ansatz (explizite Transformation):
- Transformiere beide Pinguin-Datenpunkte in den höherdimensionalen Raum:
- P1 → (Körpergewicht, Schnabellänge, Körpergewicht², Schnabellänge², √2·Körpergewicht·Schnabellänge)
- P2 → (Körpergewicht, Schnabellänge, Körpergewicht², Schnabellänge², √2·Körpergewicht·Schnabellänge)
- Berechne das Skalarprodukt der transformierten 5-dimensionalen Vektoren
Kernel-Trick Ansatz: Berechne direkt: K(P1, P2) = (P1 · P2 + 1)²
Vereinfacht ausgedrückt bedeutet das, dass man nicht wirklich die Pinguin-Daten nimmt, sie dann in diese 5 neuen Dimensionen transformiert und dann die Distanzberechnungen im transformierten Raum durchführt um die bestmögliche Trenngrenze zu ermitteln. Stattdessen nimmt man eine Abkürzung, die enorm Speicher und Rechenzeit einspart: Die jeweilige Kernel-Funktion kann für zwei Pinguine direkt das Skalarprodukt im transformierten Raum berechnen.
Warum ist das so viel effizienter?
- Speicher: Wir müssen nie die transformierten Features (Körpergewicht², Schnabellänge², usw.) speichern
- Rechenzeit: Statt 5 Multiplikationen und Additionen (für die 5D-Transformation) brauchen wir nur 3 einfache Operationen
- Skalierung: Bei höheren Polynomgraden wird der Unterschied dramatisch – ein Polynomial 10. Grades in 100 Dimensionen würde Milliarden transformierte Features erzeugen, aber der Kernel braucht weiterhin nur eine einzige Berechnung
RBF Kernel: Maximum Flexibility
Der Radial Basis Function (RBF) Kernel ist der flexibelste und meist verwendete Kernel in SVM. Er ist auch die Standard-Einstellung in scikit-learn: SVC(kernel='rbf'). Man kann argumentieren, dass er die Weiterführung der Transformation in einen höherdimensionalen Raum ist:
- Linearer Kernel: Arbeitet im ursprünglichen Merkmalsraum und kann nur gerade Trennlinien erstellen
- Polynomial Kernel: Transformiert in einen höherdimensionalen Raum mit fester Dimensionszahl (abhängig vom Polynomgrad)
- RBF Kernel: entspricht einer impliziten Transformation in einen unendlich-dimensionalen Hilbert-Raum und kann dadurch beliebig komplexe, gekrümmte Entscheidungsgrenzen erstellen
Der RBF-Kernel berechnet die Ähnlichkeit zwischen zwei Datenpunkten x₁ und x₂ über:
K(x₁, x₂) = exp(-γ ||x₁ - x₂||²)
- ||x₁ - x₂||²: Die quadrierte euklidische Distanz zwischen den Punkten
- γ (Gamma): Parameter, der die “Reichweite” des Einflusses steuert
- exp(): Die Exponentialfunktion, die eine Gauß’sche Glockenkurve erzeugt
Praktisch bedeutet das im Prinzip, dass jeder Support Vector von einer “Einflusssphäre” umgeben ist. Der RBF-Kernel bestimmt, wie stark ein Punkt die Klassifikation in seiner Umgebung beeinflusst:
- Identische Punkte (Distanz = 0): Maximaler Einfluss = 1
- Entfernte Punkte (große Distanz): Minimaler Einfluss ≈ 0
-
Gamma-Parameter: Steuert die Größe der “Einflusssphäre”
- Hohe γ-Werte → kleine “Sphären”, komplexere lokale Entscheidungsgrenzen
- Niedrige γ-Werte → große “Sphären”, glattere, globalere Entscheidungsgrenzen
Der RBF-Kernel ist deshalb so flexibel, weil er lokale Entscheidungen treffen kann: Verschiedene Bereiche des Merkmalsraums können völlig unterschiedliche Klassifikationsmuster haben, und der RBF-Kernel passt sich an jede Region individuell an.
Die mathematische Transformation, die der RBF-Kernel implizit durchführt, würde in einem Raum mit unendlich vielen Features resultieren. Aber genau wie bei den anderen Kernels wird durch den Kernel-Trick diese Transformation nie explizit berechnet – wir bekommen nur das Endergebnis: eine extrem flexible Entscheidungsgrenze.
Schauen wir uns das in Aktion an! Beim Betrachten von Adelie vs. Chinstrap mit den Features Körpergewicht und Flossenlänge zeigt sich eine Überlegenheit des RBF-Kernels gegenüber einem linearen Kernel:
# Bestes Szenario: Adelie vs Chinstrap mit body_mass_g + flipper_length_mm
adelie_chinstrap = penguins[penguins['species'].isin(['Adelie', 'Chinstrap'])].copy()
adelie_chinstrap = adelie_chinstrap.dropna(subset=['body_mass_g', 'flipper_length_mm'])
X_ac = adelie_chinstrap[['body_mass_g', 'flipper_length_mm']].values
y_ac = (adelie_chinstrap['species'] == 'Chinstrap').astype(int).values
# Train-Test Split
X_train_ac, X_test_ac, y_train_ac, y_test_ac = train_test_split(
X_ac, y_ac, test_size=0.3, random_state=42, stratify=y_ac
)
# Standardisierung
scaler_ac = StandardScaler()
X_train_ac_scaled = scaler_ac.fit_transform(X_train_ac)
X_test_ac_scaled = scaler_ac.transform(X_test_ac)
# Beide Kernel trainieren
svm_linear_ac = SVC(kernel='linear', random_state=42)
svm_rbf_ac = SVC(kernel='rbf', random_state=42)
svm_linear_ac.fit(X_train_ac_scaled, y_train_ac);
svm_rbf_ac.fit(X_train_ac_scaled, y_train_ac);
# Performance vergleichen
linear_train_acc = svm_linear_ac.score(X_train_ac_scaled, y_train_ac)
linear_test_acc = svm_linear_ac.score(X_test_ac_scaled, y_test_ac)
rbf_train_acc = svm_rbf_ac.score(X_train_ac_scaled, y_train_ac)
rbf_test_acc = svm_rbf_ac.score(X_test_ac_scaled, y_test_ac)
print(f"Performance Vergleich:")
print(f"Linear SVM - Training: {linear_train_acc:.3f}, Test: {linear_test_acc:.3f}")
print(f"RBF SVM - Training: {rbf_train_acc:.3f}, Test: {rbf_test_acc:.3f}")
print(f"RBF Vorteil im Test: {rbf_test_acc - linear_test_acc:.3f}")Performance Vergleich:
Linear SVM - Training: 0.771, Test: 0.682
RBF SVM - Training: 0.771, Test: 0.727
RBF Vorteil im Test: 0.045Code zeigen/verstecken
# Visualisierung beider Kernel
fig, axes = plt.subplots(2, 2, figsize=(15, 12), layout='tight')
# Linear SVM - obere Zeile
plot_classifier(
model=svm_linear_ac,
X_train=X_train_ac_scaled,
y_train=y_train_ac,
X_test=X_test_ac_scaled,
y_test=y_test_ac,
proba=False,
xlabel='Körpergewicht (standardisiert)',
ylabel='Flossenlänge (standardisiert)',
class_colors={0: colors['Adelie'], 1: colors['Chinstrap']},
axes=axes[0, :]
)
# RBF SVM - untere Zeile
plot_classifier(
model=svm_rbf_ac,
X_train=X_train_ac_scaled,
y_train=y_train_ac,
X_test=X_test_ac_scaled,
y_test=y_test_ac,
proba=False,
xlabel='Körpergewicht (standardisiert)',
ylabel='Flossenlänge (standardisiert)',
class_colors={0: colors['Adelie'], 1: colors['Chinstrap']},
axes=axes[1, :]
)
# Titel anpassen
axes[0, 0].set_title(f'Linear SVM - Trainingsdaten\nAccuracy: {linear_train_acc:.3f}')
axes[0, 1].set_title(f'Linear SVM - Testdaten\nAccuracy: {linear_test_acc:.3f}')
axes[1, 0].set_title(f'RBF SVM - Trainingsdaten\nAccuracy: {rbf_train_acc:.3f}')
axes[1, 1].set_title(f'RBF SVM - Testdaten\nAccuracy: {rbf_test_acc:.3f}')
fig.suptitle('Linear vs RBF SVM: Adelie vs Chinstrap\nKörpergewicht + Flossenlänge', fontsize=16)
plt.show()
Der Unterschied ist deutlich sichtbar: Während der lineare SVM eine gerade Trennlinie zieht, erstellt der RBF-Kernel komplexe, gekrümmte Entscheidungsgrenzen. Diese “Inseln” und “Buchten” in der Klassifikationsgrenze entstehen durch die lokalen “Einflusssphären” der Support Vectors.
In diesem Adelie-vs-Chinstrap-Szenario sind die Daten nicht linear trennbar – es gibt Bereiche, wo beide Arten ähnliche Kombinationen von Körpergewicht und Flossenlänge haben. Der lineare SVM kann nur eine gerade Linie ziehen und muss daher globale Kompromisse eingehen.
Der RBF-Kernel hingegen kann lokale Entscheidungen treffen: In manchen Bereichen des Merkmalsraums sind Adelie-Pinguine häufiger, in anderen Chinstrap-Pinguine. Der RBF-Kernel “lernt” diese lokalen Muster und erstellt entsprechend angepasste Entscheidungsgrenzen für jede Region.
SVM und Wahrscheinlichkeiten: Platt-Scaling
Es gilt übrigens auch hier mal wieder: SVM gibt von Haus aus keine echten Wahrscheinlichkeiten aus. Im Gegensatz zur logistischen Regression, die direkt mit Wahrscheinlichkeiten arbeitet, berechnet SVM nur eine Entscheidungsgrenze und klassifiziert Punkte als “links” oder “rechts” dieser Grenze. Dass es keine echten Wahrscheinlichkeiten gibt, kennen wir ja nun aber auch schon von Decision Trees, Random Forest und kNN. Dennoch konnte auch da mittels predict_proba() stets ein entsprechender Wert ausgegeben werden.
Das geht auch hier bei SVM, allerdings passiert das nun noch nochmal anders als bei den gerade genannten drei Methoden. Dort war es ja so, dass dann die empirische Verteilung zugrundegelegt wurde – also z.B. bei Random Forest: “Von 100 Bäumen haben 73 für Klasse A gestimmt, also ist die Wahrscheinlichkeit 0.73”. Hier gibt es nun nicht mal das, aber stattdessen kann eine nachgelagerte Berechnung durchgeführt werden, die nämlich auf dem Abstand zur Entscheidungsgrenze beruht.
Die Logik dahinter ist intuitiv: Ein Pinguin, der weit entfernt von der Grenze liegt, sollte mit hoher Sicherheit klassifiziert werden, während Grenzfälle niedrige Sicherheit haben. Scikit-learn verwendet Platt Scaling: Eine sigmoidale Funktion wandelt die rohen Abstände (Decision Scores) in Wahrscheinlichkeiten um. Große Abstände werden zu Wahrscheinlichkeiten nahe 0 oder 1, kleine Abstände zu Werten um 0.5. Was ein “großer Abstand” ist, hängt nicht von einem allgemeingültigen Wert ab, sondern vom Trainingsdatensatz und ist also einfach relativ zu dem Punkt, der am weitesten von einer Grenze entfernt ist.
Dieses Platt-Scaling funktioniert unabhängig vom gewählten Kernel (linear, polynomial, RBF).
# SVM mit Wahrscheinlichkeiten trainieren
svm_with_proba = SVC(kernel='rbf', random_state=42, probability=True)
svm_with_proba.fit(X_train_ac_scaled, y_train_ac);
# Decision Scores vs. Wahrscheinlichkeiten vergleichen
decision_scores = svm_with_proba.decision_function(X_test_ac_scaled)
probabilities = svm_with_proba.predict_proba(X_test_ac_scaled)[:, 1]
print("Decision Scores vs. Wahrscheinlichkeiten:")
print("Score\t→\tWahrscheinlichkeit")
for i in range(5):
print(f"{decision_scores[i]:6.3f}\t→\t{probabilities[i]:6.3f}")Decision Scores vs. Wahrscheinlichkeiten:
Score → Wahrscheinlichkeit
0.124 → 0.500
0.041 → 0.477
-1.132 → 0.172
0.732 → 0.686
-1.006 → 0.196Code zeigen/verstecken
# Vergleich: Harte Grenzen vs. Wahrscheinlichkeiten
fig, axes = plt.subplots(2, 2, figsize=(15, 12), layout='tight')
# Harte Klassifikationsgrenzen (oben)
plot_classifier(
model=svm_with_proba,
X_train=X_train_ac_scaled,
y_train=y_train_ac,
X_test=X_test_ac_scaled,
y_test=y_test_ac,
proba=False, # Harte Grenzen
xlabel='Körpergewicht (standardisiert)',
ylabel='Flossenlänge (standardisiert)',
class_colors={0: colors['Adelie'], 1: colors['Chinstrap']},
axes=axes[0, :]
)
# Wahrscheinlichkeits-Heatmap (unten)
plot_classifier(
model=svm_with_proba,
X_train=X_train_ac_scaled,
y_train=y_train_ac,
X_test=X_test_ac_scaled,
y_test=y_test_ac,
proba=True, # Wahrscheinlichkeiten
xlabel='Körpergewicht (standardisiert)',
ylabel='Flossenlänge (standardisiert)',
class_colors={0: colors['Adelie'], 1: colors['Chinstrap']},
axes=axes[1, :]
)
# Titel anpassen
axes[0, 0].set_title('Harte Klassifikation - Trainingsdaten')
axes[0, 1].set_title('Harte Klassifikation - Testdaten')
axes[1, 0].set_title('Wahrscheinlichkeiten - Trainingsdaten')
axes[1, 1].set_title('Wahrscheinlichkeiten - Testdaten')
fig.suptitle('RBF SVM: Harte Grenzen vs. Wahrscheinlichkeits-Heatmap\nAdelie vs Chinstrap', fontsize=16)
plt.show()
Und Achtung: probability=True muss schon beim Training gesetzt werden – man kann Wahrscheinlichkeiten nicht nachträglich “einschalten”. Das Training wird dadurch langsamer.
Methodenvergleich
Zum Abschluss führen wir einen fairen Vergleich zwischen SVM und unseren bisherigen Methoden durch:
Code zeigen/verstecken
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split, cross_val_score, RepeatedStratifiedKFold
from sklearn.preprocessing import StandardScaler
import warnings
warnings.filterwarnings('ignore')
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
# plot_classifier Funktion
def plot_classifier(model, X_train, y_train, X_test, y_test,
proba=False, xlabel=None, ylabel=None, title=None,
class_colors=None, figsize=(12, 5), axes=None):
"""
Visualisiert Klassifikationsgrenzen für ein trainiertes Modell
"""
# Subplot-Layout erstellen: 1 Zeile, 2 Spalten (nur falls keine Achsen übergeben wurden)
if axes is None:
fig, axes = plt.subplots(1, 2, figsize=figsize, sharex=True, sharey=True, layout='tight')
own_fig = True
else:
own_fig = False
# Standard-Farben (Rot & Blau) verwenden, falls keine angegeben
if class_colors is None:
class_colors = {0: 'red', 1: 'blue'}
# Custom Colormap für den Hintergrund erstellen
gradient_colors = [class_colors[0], 'white', class_colors[1]]
custom_cmap = LinearSegmentedColormap.from_list("CustomDiverging", gradient_colors, N=256)
# Gemeinsame Grenzen für beide Plots berechnen
X_all = np.vstack([X_train, X_test])
x_margin = (X_all[:, 0].max() - X_all[:, 0].min()) * 0.05
y_margin = (X_all[:, 1].max() - X_all[:, 1].min()) * 0.05
x_min = X_all[:, 0].min() - x_margin
x_max = X_all[:, 0].max() + x_margin
y_min = X_all[:, 1].min() - y_margin
y_max = X_all[:, 1].max() + y_margin
# Meshgrid für Hintergrund-Vorhersagen erstellen
xx, yy = np.meshgrid(
np.linspace(x_min, x_max, 1000),
np.linspace(y_min, y_max, 1000)
)
# Vorhersagen für jeden Punkt im Grid
if proba:
# Wahrscheinlichkeiten für Klasse 1
zz = model.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1].reshape(xx.shape)
else:
# Klassenlabels (0 oder 1)
zz = model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
# Beide Subplots (Training und Test) erstellen
for ax, X, y, subset in zip(axes, [X_train, X_test], [y_train, y_test],
["Trainingsdaten", "Testdaten"]):
# Vorhersagen für die aktuellen Daten
y_pred = model.predict(X)
# Hintergrund mit Klassifikationsgrenzen zeichnen
if proba:
# Kontinuierliche Wahrscheinlichkeiten als Heatmap
ax.imshow(zz, origin="lower", aspect="auto",
extent=(x_min, x_max, y_min, y_max),
vmin=0, vmax=1, alpha=0.25, cmap=custom_cmap);
else:
# Diskrete Klassengrenzen
ax.contourf(xx, yy, zz,
alpha=0.25,
vmin=0, vmax=1,
levels=[-0.5, 0.5, 1.5],
colors=[class_colors[0], class_colors[1]]);
# Datenpunkte zeichnen
face_colors = [class_colors[int(label)] for label in y]
edge_colors = ['black' if true_label == pred_label else 'red'
for true_label, pred_label in zip(y, y_pred)]
ax.scatter(X[:, 0], X[:, 1],
c=face_colors,
edgecolor=edge_colors,
linewidth=1,
s=50);
# Subplot-Eigenschaften setzen
ax.set_title(subset);
ax.set_xlim(x_min, x_max);
ax.set_ylim(y_min, y_max);
if xlabel:
ax.set_xlabel(xlabel);
if ylabel:
ax.set_ylabel(ylabel);
# Daten vorbereiten: Adelie vs Gentoo mit Schnabellänge + Schnabeltiefe
penguins_2d = penguins[penguins['species'].isin(['Adelie', 'Gentoo'])].copy()
penguins_2d = penguins_2d.dropna(subset=['bill_length_mm', 'bill_depth_mm'])
X_2d = penguins_2d[['bill_length_mm', 'bill_depth_mm']].values
y_2d = (penguins_2d['species'] == 'Gentoo').astype(int).values
# Train-Test Split
X_train_2d, X_test_2d, y_train_2d, y_test_2d = train_test_split(
X_2d, y_2d, test_size=0.3, random_state=42, stratify=y_2d
)
# Standardisierung (wichtig für SVM und kNN!)
scaler_2d = StandardScaler()
X_train_2d_scaled = scaler_2d.fit_transform(X_train_2d)
X_test_2d_scaled = scaler_2d.transform(X_test_2d)
# Systematischer Modellvergleich mit Kreuzvalidierung
models = {
'Logistic Regression': LogisticRegression(random_state=42),
'Decision Tree': DecisionTreeClassifier(max_depth=4, random_state=42),
'Random Forest': RandomForestClassifier(n_estimators=100, max_depth=4, random_state=42),
'K-Nearest Neighbors': KNeighborsClassifier(n_neighbors=5),
'Linear SVM': SVC(kernel='linear', random_state=42, probability=True),
'RBF SVM': SVC(kernel='rbf', random_state=42, probability=True)
}
# Verwende die gut trennbaren Adelie vs Gentoo Daten
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=10, random_state=42)
cv_results = {}
for name, model in models.items():
scores = cross_val_score(model, X_train_2d_scaled, y_train_2d, cv=cv, scoring='accuracy')
cv_results[name] = {
'scores': scores,
'mean': scores.mean(),
'std': scores.std()
}
# Ergebnisse zusammenfassen
results_summary = []
for name in models.keys():
results_summary.append({
'Methode': name,
'CV Accuracy (Mittel)': cv_results[name]['mean'],
'CV Accuracy (Std)': cv_results[name]['std']
})
results_df = pd.DataFrame(results_summary)
results_df = results_df.sort_values('CV Accuracy (Mittel)', ascending=False)
# Alle Modelle trainieren für Visualisierung
trained_models = {}
for name, model in models.items():
model.fit(X_train_2d_scaled, y_train_2d);
trained_models[name] = model
# Kombinierte Visualisierung: 6 Zeilen, 2 Spalten (eine Zeile pro Methode)
fig, axes = plt.subplots(6, 2, figsize=(15, 24), layout='tight', sharex=True, sharey=True)
method_order = ['Logistic Regression', 'Decision Tree', 'Random Forest',
'K-Nearest Neighbors', 'Linear SVM', 'RBF SVM']
for i, method_name in enumerate(method_order):
model = trained_models[method_name]
cv_score = results_df[results_df['Methode'] == method_name]['CV Accuracy (Mittel)'].iloc[0]
# Verwende plot_classifier für diese Zeile
plot_classifier(
model=model,
X_train=X_train_2d_scaled,
y_train=y_train_2d,
X_test=X_test_2d_scaled,
y_test=y_test_2d,
proba=True,
xlabel='Schnabellänge (standardisiert)',
ylabel='Schnabeltiefe (standardisiert)',
class_colors={0: colors['Adelie'], 1: colors['Gentoo']},
axes=axes[i, :]
)
# Titel anpassen mit CV-Score
axes[i, 0].set_title(f'{method_name} - Trainingsdaten\nCV Accuracy: {cv_score:.4f}')
axes[i, 1].set_title(f'{method_name} - Testdaten\nCV Accuracy: {cv_score:.4f}')
plt.show()
# Ergebnisse anzeigen
results_dfSVC(probability=True, random_state=42)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| C | 1.0 | |
| kernel | 'rbf' | |
| degree | 3 | |
| gamma | 'scale' | |
| coef0 | 0.0 | |
| shrinking | True | |
| probability | True | |
| tol | 0.001 | |
| cache_size | 200 | |
| class_weight | None | |
| verbose | False | |
| max_iter | -1 | |
| decision_function_shape | 'ovr' | |
| break_ties | False | |
| random_state | 42 |
Methode CV Accuracy (Mittel) CV Accuracy (Std)
0 Logistic Regression 0.994750 0.010500
2 Random Forest 0.994750 0.010500
4 Linear SVM 0.994750 0.010500
3 K-Nearest Neighbors 0.994750 0.010500
5 RBF SVM 0.994750 0.010500
1 Decision Tree 0.990567 0.013635Zusammenfassung: Support Vector Machines
Support Vector Machines verfolgen einen geometrischen Ansatz: Sie suchen die optimale Trenngrenze zwischen Klassen, die gleichzeitig die Margin maximiert und Fehlklassifikationen minimiert. Der C-Parameter kontrolliert diesen Kompromiss. Die drei wichtigsten Kernel:
- Linear: Gerade Trennlinien, schnell, gut interpretierbar
-
Polynomial: Komplexere Kurven durch Transformation in höhere Dimensionen
- RBF (Radial Basis Function): Maximum Flexibilität durch lokale “Einflusssphären”, kann beliebig komplexe Entscheidungsgrenzen erstellen
Der Kernel-Trick ermöglicht komplexe Transformationen ohne explizite Berechnung der höherdimensionalen Features – eine elegante mathematische Abkürzung.
Wahrscheinlichkeiten sind via Platt Scaling verfügbar (probability=True): Abstände zur Entscheidungsgrenze werden durch eine sigmoidale Funktion in approximative Wahrscheinlichkeiten umgewandelt.
Stärken: Effektiv bei vielen Features, speichereffizient (nur Support Vectors), vielseitig durch verschiedene Kernel, mathematisch fundiert.
Schwächen: Zwingend Feature-Scaling erforderlich, langsam bei großen Datensätzen (>10.000 Samples), Hyperparameter-Tuning für C und Kernel-Parameter nötig, approximative Wahrscheinlichkeiten.