import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
import seaborn as sns
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split, cross_validate, RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.metrics import classification_report
np.random.seed(42)Principal Component Analysis (PCA)
Bisher haben wir in diesem Kurs ausschließlich Methoden des überwachten Lernens (supervised learning) kennengelernt. Mit der Principal Component Analysis (PCA) lernen wir nun unsere erste Methode des unüberwachten Lernens (unsupervised learning) kennen. Beim unüberwachten Lernen haben wir nur die Inputs (X), aber kein bekanntes Ergebnis - das Verfahren muss selbst Muster oder Strukturen in den Daten finden.
Beim überwachten Lernen haben wir Beispieldaten, wo wir bereits wissen, was “herausgekommen” ist - wir haben Input (X) und das dazugehörige Ergebnis (y). Das Modell lernt anhand dieser Beispiele, für neue Inputs das Ergebnis vorherzusagen.
Beim unüberwachten Lernen haben wir nur die Inputs, aber kein bekanntes Ergebnis - das Modell muss selbst Muster oder Strukturen in den Daten finden.
Zur weiteren Einordnung: “The term unsupervised learning refers to statistical methods that extract meaning from data without training a model on labeled data (data where an outcome of interest is known). […] the goal [of supervised learning] is to build a model (set of rules) to predict a response variable from a set of predictor variables. This is supervised learning. In contrast, unsupervised learning also constructs a model of the data, but it does not distinguish between a response variable and predictor variables.” (Gedeck, Bruce & Bruce, 2020)
PCA ist eine Methode zur Dimensionsreduktion, die hochdimensionale Daten in einen niedrigdimensionalen Raum transformiert, während sie dabei die wichtigsten Informationen erhält. Sie kann sowohl als eigenständige Explorationstechnik als auch als Preprocessing-Schritt für nachgelagerte Machine Learning-Methoden verwendet werden.
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
Motivation: Warum Dimensionsreduktion?
Die Motivation für Dimensionsreduktion ergibt sich aus mehreren praktischen Problemen:
1. Visualisierung: Mehr als 3 Dimensionen können wir Menschen nicht mehr direkt visualisieren. PCA hilft uns, hochdimensionale Daten in 2D oder 3D darzustellen.
2. Curse of Dimensionality: Wie wir bereits bei k-Nearest Neighbors gesehen haben, können zu viele Features die Performance von ML-Algorithmen verschlechtern. In hochdimensionalen Räumen werden Distanzen weniger aussagekräftig.
3. Redundante Features: Oft sind Features miteinander korreliert und enthalten ähnliche Informationen. PCA kann diese Redundanz reduzieren.
4. Effizienz: Weniger Dimensionen bedeuten schnellere Berechnungen und weniger Speicherbedarf.
5. Rauschen: PCA kann helfen, das wichtige Signal vom unwichtigen Rauschen zu trennen.
Bei unseren Palmer Penguins haben wir beispielsweise 4 numerische Features. Anstatt alle 4 zu verwenden, könnten wir sie auf 2 Hauptkomponenten reduzieren, die den Großteil der Information beibehalten, aber einfacher zu handhaben sind.
Eins muss von Anfang an klar sein: Wenn wir hier von Dimensionsreduktion sprechen und davon, dass wir erst viele und dann weniger Features haben, dann ist nicht gemeint, dass wir einfach nur die wichtigsten Features behalten. Stattdessen werden bei der PCA neue Features erzeugt, die im Grunde Kombinationen aus den originalen Features sind, aber letztendlich trotzdem einheitslose, schwer greifbare Werte.
Intuition am 2D-Beispiel
Um die Grundidee von PCA zu verstehen, beginnen wir mit einem einfachen 2D-Beispiel. Wir verwenden nur Adelie-Pinguine und betrachten nur zwei Features: flipper_length_mm und body_mass_g.
Bei der PCA müssen wir auch unbedingt wieder alle Features standardisieren, da sonst beispielsweise hier body_mass_g automatisch domieren würde. Nach kNN und SVM ist PCA also nun die dritte Methode in diesem Kurs, die standardisierte Daten benötigt.
# Nur Adelie Pinguine für einfachen Einstieg
adelie_data = penguins[penguins['species'] == 'Adelie'].dropna(subset=['flipper_length_mm', 'body_mass_g'])
# Daten für 2D PCA vorbereiten
X_2d = adelie_data[['flipper_length_mm', 'body_mass_g']].values
feature_names_2d = ['flipper_length_mm', 'body_mass_g']
# Daten standardisieren
scaler = StandardScaler()
X_2d_scaled = scaler.fit_transform(X_2d)Jetzt führen wir PCA auf die standardisierten Daten durch. Dazu nutzen wir die Funktion PCA() - mal wieder aus dem scikit-learn Modul. Ohne zu wissen was genau passiert ist, lassen wir uns direkt auch mal die explained_variance_ratio_ mit ausgeben:
pca_std = PCA()
X_pca_std = pca_std.fit_transform(X_2d_scaled)
print(f"Explained variance ratio: {pca_std.explained_variance_ratio_}")Explained variance ratio: [0.73410085 0.26589915]Wir sehen, dass es bei der explained variance ratio zwei Werte gibt: 73,4% und 26,6%. Das liegt daran, dass eine PCA grundlegend genau so viele Principal Components (=Hauptkomponenten) erzeugt, wie es Dimensionen in den Daten gibt - also sprich so viele wie wir Features haben.
Am meisten hilft es wohl dem Verständnis, wenn wir uns erstmal folgende Abbildungen anschauen:
Code zeigen/verstecken
# 2x2 Grid: Komplette Transformation visualisieren
fig, axes = plt.subplots(2, 2, figsize=(14, 12), layout='tight')
# OBEN LINKS: Nicht-standardisierte Daten (reiner Scatterplot)
ax = axes[0, 0]
ax.scatter(X_2d[:, 0], X_2d[:, 1], color=colors['Adelie'], alpha=0.6, s=50)
ax.set_xlabel('Flipper Length (mm)')
ax.set_ylabel('Body Mass (g)')
ax.set_title('Original Features (nicht standardisiert)')
ax.grid(True, alpha=0.3)
# OBEN RECHTS: Standardisierte Features mit Eigenvektoren als Pfeile
ax = axes[0, 1]
ax.scatter(X_2d_scaled[:, 0], X_2d_scaled[:, 1], color=colors['Adelie'], alpha=0.6, s=50)
# Mittelpunkt der standardisierten Daten
center_x, center_y = X_2d_scaled.mean(axis=0)
# Bereiche der standardisierten Daten für Skalierung
x_range = X_2d_scaled[:, 0].max() - X_2d_scaled[:, 0].min()
y_range = X_2d_scaled[:, 1].max() - X_2d_scaled[:, 1].min()
max_range = max(x_range, y_range)
# Pfeillängen proportional zu explained variance ratio
base_length = max_range * 0.4
pc1_length = base_length * np.sqrt(pca_std.explained_variance_ratio_[0])
pc2_length = base_length * np.sqrt(pca_std.explained_variance_ratio_[1])
# PC1 Pfeil (rot)
pc1_vector = pca_std.components_[0]
pc1_dx = pc1_vector[0] * pc1_length
pc1_dy = pc1_vector[1] * pc1_length
ax.arrow(center_x, center_y, pc1_dx, pc1_dy,
color='red', linewidth=3, head_width=max_range*0.03,
head_length=max_range*0.04, alpha=0.8, length_includes_head=True)
ax.text(center_x + pc1_dx * 1.15, center_y + pc1_dy * 1.15, 'PC1',
fontsize=12, fontweight='bold', color='red', ha='center', va='center')
# PC2 Pfeil (blau)
pc2_vector = pca_std.components_[1]
pc2_dx = pc2_vector[0] * pc2_length
pc2_dy = pc2_vector[1] * pc2_length
ax.arrow(center_x, center_y, pc2_dx, pc2_dy,
color='blue', linewidth=3, head_width=max_range*0.03,
head_length=max_range*0.04, alpha=0.8, length_includes_head=True)
ax.text(center_x + pc2_dx * 1.15, center_y + pc2_dy * 1.15, 'PC2',
fontsize=12, fontweight='bold', color='blue', ha='center', va='center')
ax.set_xlabel('Flipper Length (standardized)')
ax.set_ylabel('Body Mass (standardized)')
ax.set_title('Standardized Features')
ax.grid(True, alpha=0.3)
# UNTEN LINKS: PCA-transformierte Daten
ax = axes[1, 0]
ax.scatter(X_pca_std[:, 0], X_pca_std[:, 1], color=colors['Adelie'], alpha=0.6, s=50)
# In transformierten Koordinaten sind PC1 und PC2 die Achsen
pc_x_range = X_pca_std[:, 0].max() - X_pca_std[:, 0].min()
pc_y_range = X_pca_std[:, 1].max() - X_pca_std[:, 1].min()
pc_max_range = max(pc_x_range, pc_y_range)
# Pfeile entlang der transformierten Achsen (proportional zu explained variance)
pc1_transformed_length = pc_max_range * 0.4 * np.sqrt(pca_std.explained_variance_ratio_[0])
pc2_transformed_length = pc_max_range * 0.4 * np.sqrt(pca_std.explained_variance_ratio_[1])
# PC1 entlang x-Achse (rot)
ax.arrow(0, 0, pc1_transformed_length, 0,
color='red', linewidth=3, head_width=pc_max_range*0.04,
head_length=pc_max_range*0.05, alpha=0.8, length_includes_head=True)
ax.text(pc1_transformed_length * 1.1, 0, 'PC1',
fontsize=12, fontweight='bold', color='red', ha='center', va='center')
# PC2 entlang y-Achse (blau)
ax.arrow(0, 0, 0, pc2_transformed_length,
color='blue', linewidth=3, head_width=pc_max_range*0.04,
head_length=pc_max_range*0.05, alpha=0.8, length_includes_head=True)
ax.text(0, pc2_transformed_length * 1.1, 'PC2',
fontsize=12, fontweight='bold', color='blue', ha='center', va='center')
ax.set_xlabel('Size (PC1)')
ax.set_ylabel('Shape (PC2)')
ax.set_title('Principal Components')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='black', linestyle='--', alpha=0.5)
ax.axvline(x=0, color='black', linestyle='--', alpha=0.5)
# UNTEN RECHTS: Leer lassen
ax = axes[1, 1]
ax.set_visible(False)
plt.suptitle('PCA Transformation: Von Original zu Principal Components', fontsize=16)
plt.show()
Oben links ist einfach nur der einfache Scatter-Plot aller Datenpunkte unserer zwei Features auf ihrer originalen Skala.
Oben rechts ist prinzipiell derselbe Plot zu sehen, allerdings erkennt man an den Achsen, dass es nun die standardisierte Skala ist. Auf diesen Werten wurde die PCA durchgeführt und wir erkennen auch zwei Pfeile, die deutlich machen sollen wie die Hauptkomponenten (Principal Components) nun berechnet wurden.
Einfach ausgedrückt versucht eine PCA nämlich im gesamten Datenraum (hier 2D) die “Richtung” zu finden, in der die meiste Varianz vorhanden ist. Diese Richtung wird dann der ersten Hauptkomponente zugeordnet (=PC1). Betrachtet man die Verteilung der Punkte des Scatterplots, so entspricht die Richtung des roten Pfeils genau der Linie durch die Punktewolke, “wo am meisten Musik drin ist”, also wo die Punkte am meisten streuen.
Die zweite Hauptkomponente muss immer orthogonal/senkrecht zur ersten stehen, also in dieser 2D-Ebene im 90 Grad Winkel zu ihr. Prinzipiell bildet die zweite Hauptkomponente eben immer die “Richtung” ab, wo nach PC1 eben am zweitmeisten Varianz vorhanden ist - aber eben unbedingt orthogonal zu PC1. Da es hier aber nur zwei Dimensionen und somit auch nur zwei Hauptkomponenten gibt, ist PC2 hier auch schlichtweg “alles was PC1 nicht fassen konnte”, also die gesamte Restvarianz. Übrigens bedeutet das auch ganz konkret: Hauptkomponenten sind immer orthogonal, also unkorreliert zueinander. Jede neue Komponente erfasst ausschließlich Varianz, die von den vorherigen noch nicht erklärt wurde.
Unten links sehen wir quasi die Abbildung von oben rechts, aber so rotiert, dass die beiden Hauptkomponenten nun die Achsen sind. Die Idee ist also: Anstatt die Daten mit den ursprünglichen Features flipper_length_mm und body_mass_g zu beschreiben, beschreiben wir sie mit den neuen Features PC1 und PC2, die die Richtungen maximaler Varianz repräsentieren. Die so durch die PCA transformierten Datenpunkte bezeichnet man als Scores.
Und genau das passiert immer bei einer PCA, wird aber erst so richtig nützlich wenn wir davor mehr Dimensionen hatten als danach - nicht wie hier vorher zwei und nachher zwei.
Die Mathematik dahinter
Das ganze jetzt visuell verstanden zu haben ist gut: Wir suchen immer genau die “Richtungen/Pfeile”, die die meiste Varianz im Datenraum erfassen. Funktionieren tut das Ganze aber mittels recht abstrakter Mathematik: Eigenwerten und Eigenvektoren der Kovarianzmatrix und in Python z.B. via np.linalg.eig(np.cov(X_2d_scaled.T)). Schauen wir uns an, wie das funktioniert - mit den standardisierten Daten:
# Kovarianzmatrix berechnen
cov_matrix = np.cov(X_2d_scaled.T)
print("\nKovarianzmatrix (standardisierte Daten):")
print(cov_matrix)
# Eigenwerte und Eigenvektoren berechnen
eigenvalues, eigenvectors = np.linalg.eig(cov_matrix)
# Nach Eigenwerten sortieren (absteigend)
idx = eigenvalues.argsort()[::-1]
eigenvalues = eigenvalues[idx]
eigenvectors = eigenvectors[:, idx]
print("\nEigenwerte (manuell berechnet):")
print(eigenvalues)
print("\nEigenvektoren (manuell berechnet):")
print(eigenvectors)
# Vergleich mit sklearn
print("\nVergleich mit sklearn:")
print(f"Eigenwerte sklearn: {pca_std.explained_variance_}")
print(f"Eigenvektoren sklearn:\n{pca_std.components_}")
Kovarianzmatrix (standardisierte Daten):
[[1.00666667 0.47132304]
[0.47132304 1.00666667]]
Eigenwerte (manuell berechnet):
[1.47798971 0.53534363]
Eigenvektoren (manuell berechnet):
[[ 0.70710678 -0.70710678]
[ 0.70710678 0.70710678]]
Vergleich mit sklearn:
Eigenwerte sklearn: [1.47798971 0.53534363]
Eigenvektoren sklearn:
[[ 0.70710678 0.70710678]
[-0.70710678 0.70710678]]- Kovarianzmatrix berechnen: \(\mathbf{C} = \frac{1}{n-1}\mathbf{X}^T\mathbf{X}\)
-
Eigenwerte und Eigenvektoren finden: \(\mathbf{C}\mathbf{v} = \lambda\mathbf{v}\)
- \(\mathbf{v}\) sind die Eigenvektoren (Richtungen der Hauptkomponenten)
- \(\lambda\) sind die Eigenwerte (Varianz in diese Richtungen)
- Nach Eigenwerten sortieren: Die Hauptkomponenten werden nach der Wichtigkeit (Eigenwert) geordnet
Es sind also die Eigenvektoren der Kovarianzmatrix, die die die Richtungen anzeigen, in denen die Daten am meisten variieren. Der erste Eigenvektor zeigt die Richtung der maximalen Varianz, der zweite die der zweitgrößten Varianz (orthogonal zum ersten), und so weiter.
Akzeptiert man also, dass auf diese Weise die Kovarianzmatrix und dann die Eigenwerte und Eigenvektoren berechnet werden können, sind es schlichtweg diese Schritte, die nötig sind. Möchte man allerdings genau verstehen warum und wie das tatsächlich mathematisch funktioniert, hilft ggf. dieses Video. Wenn nicht, kann man wohl nachvollziehen wie es zu diesem Meme kam:

Beispiel mit mehr Features
Nachdem wir die Grundidee mit 2 Features verstanden haben, wenden wir PCA nun auf alle verfügbaren numerischen Features aller Palmer Penguins an:
# Alle numerischen Features verwenden
numeric_features = ['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']
penguins_clean = penguins.dropna(subset=numeric_features + ['species'])
print(f"Vollständiger Datensatz nach Bereinigung: {len(penguins_clean)} Pinguine")
print(f"Verwendet Features: {numeric_features}")
# Daten vorbereiten
X_full = penguins_clean[numeric_features].values
y_species = penguins_clean['species'].values
# Standardisierung
scaler_full = StandardScaler()
X_full_scaled = scaler_full.fit_transform(X_full)
# PCA
pca_full = PCA()
X_pca_full = pca_full.fit_transform(X_full_scaled)
print("\nPCA mit allen Features:")
print(f"Explained variance ratio: {pca_full.explained_variance_ratio_}")
print(f"Cumulative explained variance: {pca_full.explained_variance_ratio_.cumsum()}")Vollständiger Datensatz nach Bereinigung: 342 Pinguine
Verwendet Features: ['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']
PCA mit allen Features:
Explained variance ratio: [0.68843878 0.19312919 0.09130898 0.02712305]
Cumulative explained variance: [0.68843878 0.88156797 0.97287695 1. ]Es wurde jetzt also in einem 4-Dimensionalen Raum erstmal die Richtung gefunden, die am meisten Varianz erklärt und diese wurde PC1 zugeordnet. Orthogonal zu PC1 wurde dann die Richtung gefunden, die im verbleibenden Raum eben am zweitemeisten erklärt und das ist PC2. Und dann eben weiter mit PC3 und PC4. Dabei kam heraus:
- PC1: Erklärt 68,8% der Gesamtvarianz
- PC2: Erklärt weitere 19,3% (zusammen 88,2%)
- PC3: Erklärt weitere 9,1% (zusammen 97,3%)
- PC4: Erklärt die restlichen 2,7%
Mit nur den ersten zwei Hauptkomponenten zusammen können wir also mit 2 Features bereits 88% der Varianz erklären! Falls uns das noch nicht reicht, können wir auch noch PC3 dazuholen und so mit 3 Features 97,3% der Varianz erklären. In beiden Fällen haben wir die Anzahl der Features reduziert ohne allzu viel Information zu verlieren.
Also Faustregel gilt, dass man so viele Hauptkomponenten berücksichtigen sollte bis die kumulative Summe der erklärten Varianz bei 80-95% liegt.
Scree Plot
Die erklärte Varianz je Hauptkomponente stellt man üblicherweise in einem sogenannten Scree-Plot1 und deren kumulative Summe wie folgt dar:
# Scree Plot
fig, axes = plt.subplots(1, 2, figsize=(14, 5), layout='tight')
# Scree Plot
ax = axes[0]
ax.plot(range(1, len(pca_full.explained_variance_ratio_) + 1),
pca_full.explained_variance_ratio_, 'bo-', linewidth=2, markersize=8)
ax.set_ylim(0, 1);
ax.xaxis.set_major_locator(MaxNLocator(integer=True))
ax.set_xlabel('Principal Component')
ax.set_ylabel('Explained Variance Ratio')
ax.set_title('Scree Plot')
ax.grid(True, alpha=0.3)
# Cumulative explained variance
ax = axes[1]
ax.plot(range(1, len(pca_full.explained_variance_ratio_) + 1),
pca_full.explained_variance_ratio_.cumsum(), 'ro-', linewidth=2, markersize=8)
ax.axhline(y=0.95, color='gray', linestyle='--', alpha=0.7, label='95% Varianz')
ax.set_ylim(0, 1);
ax.xaxis.set_major_locator(MaxNLocator(integer=True))
ax.set_xlabel('Principal Component')
ax.set_ylabel('Cumulative Explained Variance')
ax.set_title('Cumulative Explained Variance')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
Die beiden Plots mit idealerweise gut sichtbaren Knicks helfen bei der Entscheidung, wie viele Komponenten man behalten sollte. Hier wären vermutlich zwei Hauptkomponenten genug.
Anstatt manuell im Scree-Plot nach einem „Knick“ zu suchen, kann man den Parameter n_components auch als Anteil der zu erklärenden Varianz angeben (z. B. 0.95).
from sklearn.decomposition import PCA
# Behalte so viele Hauptkomponenten, dass mind. 95% der Varianz erklärt sind
pca = PCA(n_components=0.95, svd_solver="full")
X_pca = pca.fit_transform(X_full_scaled)Das ist besonders praktisch, wenn man keinen bestimmten Plot (z. B. 2D/3D) im Kopf hat, sondern einfach möglichst viele Informationen bei möglichst geringer Dimension erhalten möchte.
Scores
Wie schon beim 2D-Beispiel können wir auch hier die Scores, also die transformierten Datenpunkte, visualisieren. Ursprünglich lagen die Daten ja in einem 4-Dimensionalen Raum vor, da wir uns aber entschieden haben diese Informationen nun nur noch durch die 2 Hauptkomponenten abzubilden, können wir also wieder einen einfachen Scatter-Plot mit PC1 auf der x-Achse und PC2 auf der y-Achse zeichnen:
# PCA mit 2 Komponenten für Visualisierung
pca_2comp = PCA()
X_pca_2comp = pca_2comp.fit_transform(X_full_scaled)
var_sum = pca_2comp.explained_variance_ratio_[:2].sum()
# Biplot mit allen drei Arten
fig, ax = plt.subplots(figsize=(10, 8), layout='tight')
# Datenpunkte nach Art färben
for species in colors.keys():
mask = y_species == species
ax.scatter(X_pca_2comp[mask, 0], X_pca_2comp[mask, 1],
c=colors[species], label=species, alpha=0.6, s=50)
ax.set_xlabel(f'PC1 ({pca_2comp.explained_variance_ratio_[0]:.1%} Varianz)')
ax.set_ylabel(f'PC2 ({pca_2comp.explained_variance_ratio_[1]:.1%} Varianz)')
ax.set_title(f'PCA (PC1+PC2 = {var_sum:.1%} Varianz)')
ax.legend()
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='black', linestyle='-', alpha=0.3)
ax.axvline(x=0, color='black', linestyle='-', alpha=0.3)
ax.set_aspect('equal', adjustable='box')
plt.show()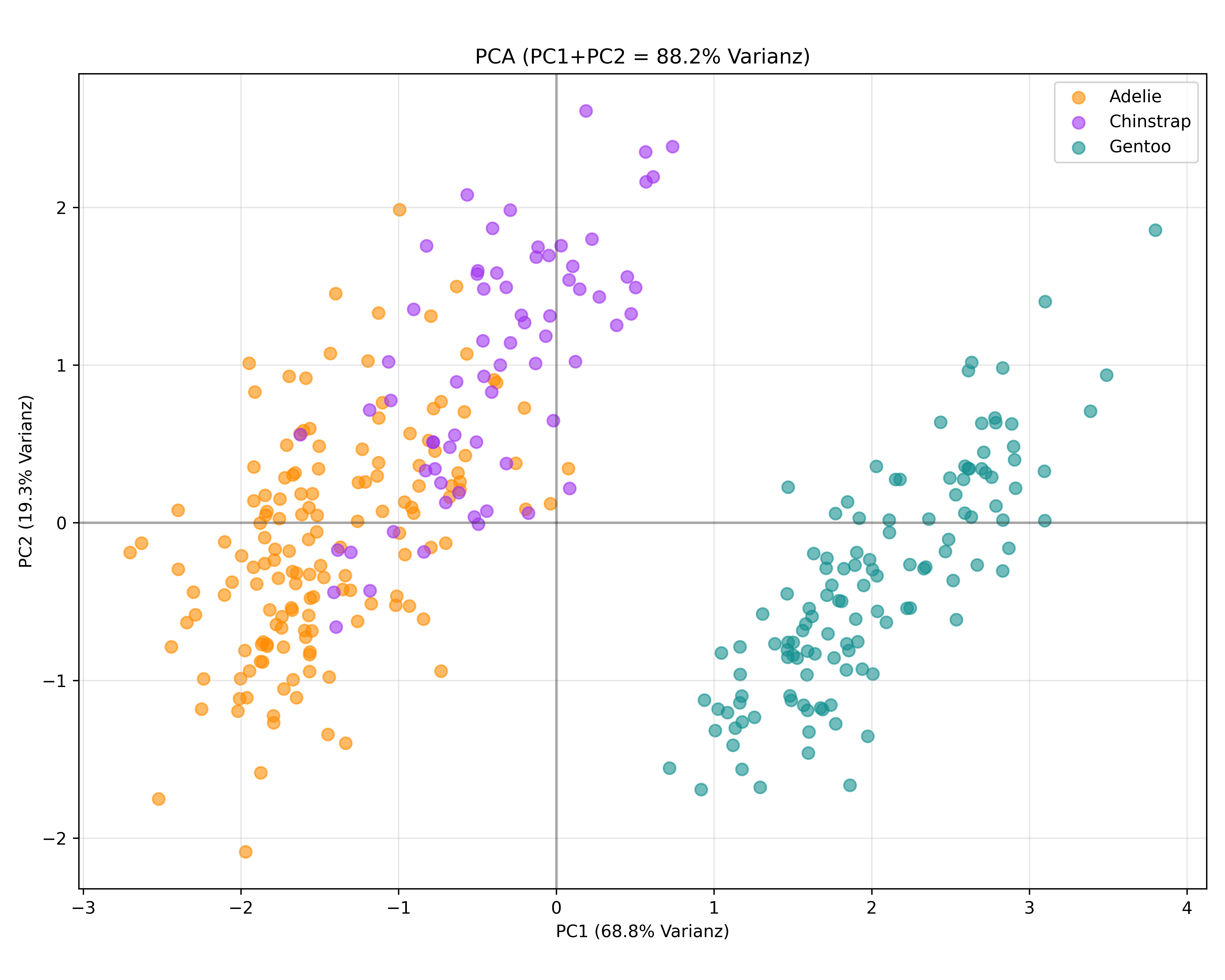
Wir sehen also einen Scatter-Plot. In diesem Plot haben wir sogar jeden Punkt entsprechend der Art eingefärbt - es muss aber klar sein, dass die Information der Pinguinart bei der PCA überhaupt nicht berücksichtigt, sondern einfach jetzt nachträglich wieder herangezogen wurde.
Und spätestens hier wird also deutlich, dass der Plot zwar recht informativ aussieht - im Sinne von Punkten, die relativ viel streuen bzw. Muster zeigen - aber eben “nur” Hauptkomponenten auf den Achsen hat und demnach keine greifbaren, echten Merkmale von Pinguinen.
Wir können zum Vergleich ja mal schauen wie alle 2D-Scatter-Plots basierend auf den originalen Features im Vergleich ausehen würden:
Code zeigen/verstecken
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from itertools import combinations
# Alle x- und y-Werte für globale Limits sammeln
all_x_values = []
all_y_values = []
# PCA-Daten hinzufügen
all_x_values.extend(X_pca_2comp[:, 0])
all_y_values.extend(X_pca_2comp[:, 1])
# Varianz jedes Features berechnen für Reihenfolge-Entscheidung
feature_variances = {feature: penguins_clean[feature].var() for feature in numeric_features}
# Alle 2er-Kombinationen generieren und nach Varianz sortieren
feature_combinations_raw = list(combinations(numeric_features, 2))
feature_combinations = []
for f1, f2 in feature_combinations_raw:
# Feature mit höherer Varianz auf x-Achse
if feature_variances[f1] >= feature_variances[f2]:
feature_combinations.append((f1, f2)) # f1 auf x-Achse
else:
feature_combinations.append((f2, f1)) # f2 auf x-Achse
# Standardisierte Feature-Kombinationen zu globalen Limits hinzufügen
penguins_scaled = penguins_clean.copy()
penguins_scaled[numeric_features] = X_full_scaled
for feature_x, feature_y in feature_combinations:
all_x_values.extend(penguins_scaled[feature_x])
all_y_values.extend(penguins_scaled[feature_y])
# Globale Limits berechnen
global_x_min, global_x_max = min(all_x_values), max(all_x_values)
global_y_min, global_y_max = min(all_y_values), max(all_y_values)
# Etwas Padding hinzufügen
x_lim = [global_x_min - 0.3, global_x_max + 0.3]
y_lim = [global_y_min - 0.3, global_y_max + 0.2]
# PCA-spezifische Limits für Referenz-Rechteck
pca_x_min, pca_x_max = X_pca_2comp[:, 0].min(), X_pca_2comp[:, 0].max()
pca_y_min, pca_y_max = X_pca_2comp[:, 1].min(), X_pca_2comp[:, 1].max()
# Figure mit komplexem Grid Layout (3 Spalten, 4 Zeilen)
fig = plt.figure(figsize=(15, 12))
# PCA Plot: nimmt die ersten 2 Zeilen komplett ein (rowspan=2, colspan=3)
ax_pca = plt.subplot2grid((4, 3), (0, 0), rowspan=2, colspan=3)
# Referenz-Rechteck (transparent grün, hinter den Punkten)
rect_width = pca_x_max - pca_x_min
rect_height = pca_y_max - pca_y_min
rect = plt.Rectangle((pca_x_min, pca_y_min), rect_width, rect_height,
facecolor='green', alpha=0.2, zorder=0)
ax_pca.add_patch(rect)
# PCA Datenpunkte nach Art färben
for species in colors.keys():
mask = y_species == species
ax_pca.scatter(X_pca_2comp[mask, 0], X_pca_2comp[mask, 1],
c=colors[species], label=species, alpha=0.6, s=50, zorder=2)
ax_pca.set_xlabel(f'PC1 ({pca_2comp.explained_variance_ratio_[0]:.1%} Varianz)')
ax_pca.set_ylabel(f'PC2 ({pca_2comp.explained_variance_ratio_[1]:.1%} Varianz)')
ax_pca.set_title('PCA (PC1 vs PC2)')
ax_pca.grid(True, alpha=0.3)
ax_pca.set_aspect('equal', adjustable='box')
ax_pca.set_xlim(x_lim);
ax_pca.set_ylim(y_lim);
ax_pca.axhline(y=0, color='black', linestyle='-', alpha=0.3)
ax_pca.axvline(x=0, color='black', linestyle='-', alpha=0.3)
ax_pca.legend()
# Subplots 1-6: Feature-Kombinationen in den unteren 2 Zeilen (2x3 Grid)
for i, (feature_x, feature_y) in enumerate(feature_combinations):
# Berechne Position im 2x3 Grid (Zeilen 2-3, Spalten 0-2)
row = 2 + (i // 3) # Zeile 2 oder 3
col = i % 3 # Spalte 0, 1, oder 2
ax = plt.subplot2grid((4, 3), (row, col))
# Referenz-Rechteck (transparent grün, hinter den Punkten)
rect = plt.Rectangle((pca_x_min, pca_y_min), rect_width, rect_height,
facecolor='green', alpha=0.2, zorder=0)
ax.add_patch(rect)
# Datenpunkte nach Art färben
for species in colors.keys():
mask = penguins_scaled['species'] == species
data_subset = penguins_scaled[mask]
ax.scatter(data_subset[feature_x], data_subset[feature_y],
c=colors[species], label=species, alpha=0.6, s=50, zorder=2)
# Achsenbeschriftung
ax.set_xlabel(f'{feature_x.replace("_", " ").title()} (standardized)')
ax.set_ylabel(f'{feature_y.replace("_", " ").title()} (standardized)')
ax.set_title(f'{feature_x.replace("_", " ").title()} vs {feature_y.replace("_", " ").title()}')
ax.grid(True, alpha=0.3)
ax.set_aspect('equal', adjustable='box')
ax.set_xlim(x_lim)
ax.set_ylim(y_lim)
ax.axhline(y=0, color='black', linestyle='-', alpha=0.3)
ax.axvline(x=0, color='black', linestyle='-', alpha=0.3)
# Layout anpassen
plt.tight_layout()
plt.show()
Diese Darstellung soll folgendes zeigen: Der große PCA-Plot oben zeigt PC1 vs. PC2, während die sechs kleineren Plots darunter alle möglichen Zweierkombinationen der vier ursprünglichen Features darstellen. Alle Plots verwenden dieselbe Achsenskalierung, wodurch ein direkterer Vergleich möglich wird.
Das grüne Rechteck in jedem Plot markiert genau den Datenbereich, den die PCA-Transformation ausnutzt - also von den minimalen zu den maximalen Werten im PC1-PC2-Plot. Betrachtet man nun die Datenpunkte in den sechs Original-Feature-Plots, fällt auf, dass diese meist insgesamt dichter beieinanderliegen und nicht den gesamten verfügbaren Raum des grünen Rechtecks ausnutzen.
Dies visualisiert eindrucksvoll das Grundprinzip der PCA: Während jede der Original-Feature-Kombinationen nur einen Teil der möglichen Varianz erfasst, schaffen es die beiden Hauptkomponenten, die maximale Streuung aus dem vierdimensionalen Originalraum in zwei Dimensionen zu komprimieren. Die PCA “presst” sozusagen die wichtigsten Informationen aus allen vier Features in nur zwei neue Features zusammen, wodurch 88% der ursprünglichen Varianz erhalten bleiben.
Loadings
Nachdem eine PCA neue Features (die Hauptkomponenten) erzeugt hat, könnte man ja nachträglich fragen wollen wie genau diese neuen Features aus den ursprünglichen entstanden sind? Die Antwort liefern die sogenannten Loadings - sie sind sozusagen die “Rezepte”, die uns verraten, welche Zutaten (ursprüngliche Features) in welchen Mengen in jede Hauptkomponente hineinfließen.
Nochmal anders ausgedrückt: Da eine Hauptkomponente ja durch die optimale “Richtung” des Pfeils/Eigenvektors im gesamten Datenraum abgedbildet wird, ist die Frage ob und wie sehr dieser Pfeil in die Richtung der verschiedenen Achsen/Features zeigt. In einem 3-Dimensionalen Raum kann man sich ja durchaus vorstellen, dass ein Pfeil eher nur in den x-y-Raum zeigt und kaum tief in den z-Raum eindringt. Eben diese Verteilung würde dann durch die Loadings ausgedrückt werden.
print("PCA Loadings:")
loadings_df = pd.DataFrame(
pca_2comp.components_.T,
columns=['PC1', 'PC2', 'PC3', 'PC4'],
index=numeric_features
)
print(loadings_df.round(3))PCA Loadings:
PC1 PC2 PC3 PC4
bill_length_mm 0.455 0.597 0.644 -0.146
bill_depth_mm -0.400 0.798 -0.418 0.168
flipper_length_mm 0.576 0.002 -0.232 0.784
body_mass_g 0.548 0.084 -0.597 -0.580Loadings sind die Gewichte, mit denen die ursprünglichen (standardisierten) Features zu den Hauptkomponenten kombiniert werden. Man kann sie als Linearkombinationskoeffizienten verstehen:
PC1 = 0.45×bill_length_mm + (-0.40)×bill_depth_mm + 0.57×flipper_length_mm + 0.54×body_mass_g PC2 = 0.59×bill_length_mm + 0.79×bill_depth_mm + (-0.17)×flipper_length_mm + (-0.07)×body_mass_g
Interpretation der Vorzeichen und Beträge:
- Große positive Werte (z.B. +0.798): Das ursprüngliche Feature trägt stark und in gleicher Richtung zur Hauptkomponente bei
- Große negative Werte (z.B. -0.400): Das ursprüngliche Feature trägt stark, aber in entgegengesetzter Richtung bei
- Kleine Werte (z.B. -0.075): Das ursprüngliche Feature hat wenig Einfluss auf diese Hauptkomponente
Inhaltliche Interpretation unseres Beispiels:
PC1 hat hohe positive Loadings für
flipper_length_mm(+0.576),body_mass_g(+0.548) undbill_length_mm(+0.455), aber ein negatives Loading fürbill_depth_mm(-0.400). Das deutet auf einen “Größen-Faktor” hin: Große Pinguine haben längere Flossen, mehr Gewicht und längere Schnäbel, aber tendenziell schmälere Schnäbel.PC2 hat die höchsten Loadings für
bill_depth_mm(+0.798) undbill_length_mm(+0.597), während Flossenlänge und Gewicht wenig beitragen. Das könnte einen “Schnabelform-Faktor” repräsentieren.
# Loadings Heatmap
fig, axes = plt.subplots(1, 2, figsize=(16, 6), layout='tight')
# Heatmap
ax = axes[0]
sns.heatmap(loadings_df.T, annot=True, cmap='RdBu_r', center=0,
cbar_kws={'label': 'Loading'}, ax=ax, fmt='.3f')
ax.set_title('PCA Loadings Heatmap')
# Barplot für bessere Übersicht
ax = axes[1]
x_pos = np.arange(len(numeric_features))
width = 0.35
bars1 = ax.bar(x_pos - width/2, loadings_df['PC1'], width,
label='PC1', alpha=0.8, color='darkblue')
bars2 = ax.bar(x_pos + width/2, loadings_df['PC2'], width,
label='PC2', alpha=0.8, color='darkred')
ax.set_xlabel('Features')
ax.set_ylabel('Loading')
ax.set_title('PCA Loadings (Barplot)')
ax.set_xticks(x_pos)
ax.set_xticklabels([f.replace('_mm', '').replace('_g', '') for f in numeric_features],
rotation=45, ha='right')
ax.legend()
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='black', linewidth=0.8)
plt.show()
Biplot: Loadings und Scores zusammen
# Biplot mit detaillierter Erklärung
fig, ax = plt.subplots(figsize=(12, 10), layout='tight')
# Datenpunkte (Scores) nach Art färben
for species in colors.keys():
mask = y_species == species
ax.scatter(X_pca_2comp[mask, 0], X_pca_2comp[mask, 1],
c=colors[species], label=species, alpha=0.6, s=50, zorder=2)
# Loadings als Pfeile (skaliert für bessere Sichtbarkeit)
scale_factor = 3
for i, feature in enumerate(numeric_features):
# Pfeil von Ursprung zu Loading-Position
dx = loadings_df.loc[feature, 'PC1'] * scale_factor
dy = loadings_df.loc[feature, 'PC2'] * scale_factor
ax.arrow(0, 0, dx, dy, head_width=0.15, head_length=0.15,
fc='red', ec='red', alpha=0.8, linewidth=2, zorder=3)
# Label positionieren
label_x = dx * 1.1
label_y = dy * 1.1
ax.text(label_x, label_y, feature.replace('_mm', '').replace('_g', ''),
fontsize=11, ha='center', va='center', fontweight='bold',
bbox=dict(boxstyle="round,pad=0.3", facecolor="white", alpha=0.9),
zorder=4)
ax.set_xlabel(f'PC1 ({pca_2comp.explained_variance_ratio_[0]:.1%} Varianz)')
ax.set_ylabel(f'PC2 ({pca_2comp.explained_variance_ratio_[1]:.1%} Varianz)')
ax.set_title('PCA Biplot: Scores (Punkte) und Loadings (Pfeile)\nPfeilrichtung zeigt Korrelation, Pfeillänge zeigt Einfluss')
ax.legend(title='Species')
ax.grid(True, alpha=0.3)
ax.axhline(y=0, color='black', linestyle='-', alpha=0.5)
ax.axvline(x=0, color='black', linestyle='-', alpha=0.5)
plt.show()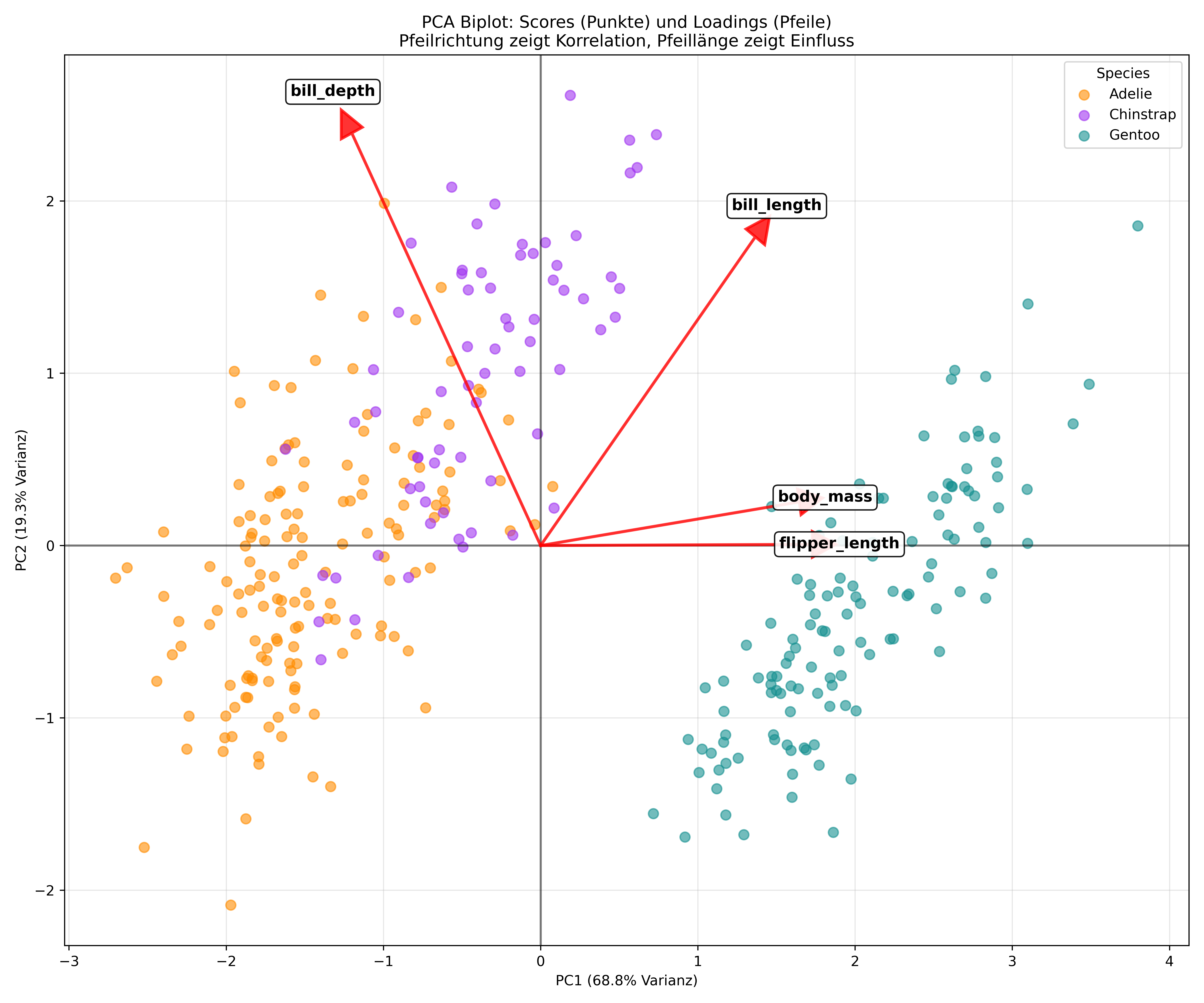
Ein Biplot ist auch eine häufige Visualisierungen in der PCA, da er zwei zentrale Informationen in einer einzigen Grafik kombiniert: die Scores (transformierte Datenpunkte) und die Loadings (ursprüngliche Features). Demnach ermöglicht sie, gleichzeitig zu sehen, wo sich die Datenpunkte im neuen PCA-Raum befinden und wie sie sich zu den ursprünglichen Messungen verhalten.
Der Name “Biplot” kommt daher, dass hier zwei verschiedene Arten von Informationen in einem Plot dargestellt werden. Während ein normaler Scatter-Plot nur die Position der Datenpunkte zeigt, fügt der Biplot die Richtungsvektoren der ursprünglichen Features hinzu. So können wir beispielsweise erkennen, dass Gentoo-Pinguine (orange Punkte) hauptsächlich im rechten Bereich des Plots liegen - genau in der Richtung, in die die Pfeile für flipper_length, body_mass und bill_length zeigen. Das bestätigt unsere Interpretation von PC1 als “Körpergröße”.
Interpretation des Biplots:
- Pfeile (Loadings): Zeigen die Richtung und Stärke des Einflusses jedes ursprünglichen Features
- Pfeillänge: Je länger, desto mehr trägt das Feature zu den dargestellten PCs bei
- Pfeilrichtung: Zeigt die Korrelationsrichtung zwischen Feature und PCs
- Winkel zwischen Pfeilen: Kleine Winkel = Features sind positiv korreliert, große Winkel (nahe 180°) = negativ korreliert
Praktische Anwendung: Feature-Interpretation
# Systematische Interpretation der Loadings
for pc in ['PC1', 'PC2']:
# Sortiere Features nach absolutem Loading-Wert
pc_loadings = loadings_df[pc].abs().sort_values(ascending=False)
print(f"{pc} ({pca_2comp.explained_variance_ratio_[['PC1', 'PC2'].index(pc)]:.1%} der Varianz):")
print(" Wichtigste Beiträge:")
for feature in pc_loadings.index[:3]: # Top 3
loading_val = loadings_df.loc[feature, pc]
direction = "positiv" if loading_val > 0 else "negativ"
print(f" • {feature}: {loading_val:.3f} ({direction})")
print()PC1 (68.8% der Varianz):
Wichtigste Beiträge:
• flipper_length_mm: 0.576 (positiv)
• body_mass_g: 0.548 (positiv)
• bill_length_mm: 0.455 (positiv)
PC2 (19.3% der Varianz):
Wichtigste Beiträge:
• bill_depth_mm: 0.798 (positiv)
• bill_length_mm: 0.597 (positiv)
• body_mass_g: 0.084 (positiv)Betrachtet man die Loadings der beiden Hauptkomponenten, wird deutlich, dass PC1 hauptsächlich von flipper_length_mm (+0.576), body_mass_g (+0.548) und bill_length_mm (+0.455) bestimmt wird, während bill_depth_mm einen negativen Beitrag (-0.400) leistet. Diese Kombination deutet darauf hin, dass PC1 eine Art “Körpergröße” repräsentiert: Pinguine mit hohen PC1-Werten haben längere Flossen, mehr Gewicht und längere Schnäbel, aber tendenziell schmalere Schnäbel.
PC2 hingegen wird hauptsächlich von bill_depth_mm (+0.798) und bill_length_mm (+0.597) dominiert, während Flossenlänge und Gewicht kaum eine Rolle spielen. Dies lässt sich als “Schnabelform” interpretieren - PC2 erfasst primär die Variation in den Schnabelabmessungen.
Diese Interpretation ist ein wichtiger Schritt in der praktischen Anwendung von PCA: Anstatt mit abstrakten mathematischen Konstrukten wie “PC1” und “PC2” zu arbeiten, können wir durch die Kombination von Fachwissen über Pinguine und den quantitativen Loading-Ergebnissen den Hauptkomponenten inhaltlich sinnvolle Namen geben. Natürlich bleiben auch “Körpergröße” und “Schnabelform” immer noch abstrakte Konzepte, da sie mathematisch gesehen nur Linearkombinationen der ursprünglichen Messungen sind. Dennoch machen solche Benennungen die Arbeit mit den transformierten Daten deutlich intuitiver und erleichtern die Kommunikation der Ergebnisse.
Grenzen und Interpretation
PCA hat sowohl Stärken als auch wichtige Limitationen:
Stärken:
- Effektive Dimensionsreduktion
- Entfernung von korrelierten Features2
- Gute Visualisierungsmöglichkeiten
- Mathematisch fundiert und stabil
Limitationen:
- Verlust der Interpretierbarkeit: PC1 ist keine direkte Messung mehr, sondern eine Linearkombination aller ursprünglichen Features
- Linearität: PCA findet nur lineare Zusammenhänge
- Standardisierung erforderlich: Features müssen meist standardisiert werden
- Alle Features einbezogen: Jede PC ist eine Kombination aller ursprünglichen Features
- Informationsverlust: Dimensionsreduktion bedeutet immer Informationsverlust
- PCA ist anfällig gegenüber Ausreißern
Wann PCA verwenden?
- Bei vielen korrelierten Features
- Für Visualisierung hochdimensionaler Daten
- Als Preprocessing bei “curse of dimensionality”
- Zur Datenexploration und Mustererkennung
Wann PCA vermeiden?
- Wenn Interpretierbarkeit einzelner Features wichtig ist
- Bei wenigen, bereits gut verständlichen Features
- Wenn nicht-lineare Beziehungen vermutet werden
Prinzipiell kann man auch kategoriale Variablen in eine PCA einbringen – indem man sie per One-Hot-Encoding (Dummy-Codierung) in numerische Spalten umwandelt. In der Praxis funktioniert das oft auch ganz gut – aber man sollte die Grenzen kennen.
Das Problem liegt darin, dass PCA Varianz im euklidischen Raum maximiert. Dummy-Variablen sind jedoch nur 0/1-Indikatoren. Ihre Varianz hängt allein von der Häufigkeit der Kategorie ab (seltene Kategorien tragen wenig, häufige dominieren). Zudem erzeugt One-Hot fast immer starke lineare Abhängigkeiten (z. B. „wenn Kategorie A=1, dann B=0“). Dadurch werden die PCs schwer interpretierbar – sie repräsentieren eher Kontraste zwischen Kategorien als wirklich sinnvolle Muster.
Um dieses Problem zu umgehen, hat man eigene Verfahren entwickelt:
MCA (Multiple Correspondence Analysis): Kann man sich als „PCA für kategoriale Variablen“ vorstellen. Statt euklidischer Distanzen arbeitet MCA mit der Chi-Quadrat-Distanz auf einer Kontingenztafel. Damit wird erfasst, wie häufig Kategorien gemeinsam auftreten, was für kategoriale Daten wesentlich sinnvoller ist.
→ In Python z. B. mitprince.MCA.FAMD (Factor Analysis of Mixed Data): Eine Erweiterung, die gemischte Datensätze (numerisch + kategorial) verarbeitet. Numerische Variablen werden wie bei PCA behandelt, kategoriale wie bei MCA. So erhält man Hauptkomponenten, die beide Datentypen integrieren.
→ In Python:prince.FAMD.
Scikit-Learn selbst bietet nur die klassische PCA (für numerische Daten) an. Wer MCA oder FAMD nutzen möchte, braucht Zusatzmodule wie prince.
Kurz gesagt: One-Hot + PCA ist möglich und kann im Alltag nützlich sein, für ausschließlich kategoriale Daten ist jedoch MCA die passendere Wahl, und für gemischte Datensätze lohnt es sich ggf. zu FAMD zu wechseln.
Zusammenfassung
Principal Component Analysis ist eine mächtige Methode für:
- Dimensionsreduktion: Reduzierung der Anzahl Features bei Erhalt der wichtigsten Information
- Datenexploration: Verstehen der Hauptvariationsrichtungen in den Daten
- Visualisierung: Darstellung hochdimensionaler Daten in 2D oder 3D
- Preprocessing: Vorbereitung für nachgelagerte ML-Algorithmen
Die wichtigsten Takeaways:
- PCA ist unüberwachtes Lernen - wir brauchen keine Zielvariable
- Standardisierung ist notwendig
- Hauptkomponenten sind orthogonal und nach Wichtigkeit sortiert
- Interpretation über Loadings (Gewichte der ursprünglichen Features)
- Trade-off zwischen Dimensionsreduktion und Informationsverlust
Übungen
In dieser Übung wirst du eine Principal Component Analysis (PCA) und anschließend eine kNN-Klassifikation mit dem Bodyfat-Datensatz durchführen. Der Datensatz enthält Körperfettmessungen und anthropometrische Daten von 252 Männern.
Der folgende Code lädt den Datensatz:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split, GridSearchCV, cross_val_score, RepeatedStratifiedKFold
from sklearn.neighbors import KNeighborsClassifier
from matplotlib.ticker import MaxNLocator
import warnings
warnings.filterwarnings('ignore')
# Datensatz laden
url = "https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/bodyfat/bodyfat.csv"
df = pd.read_csv(url)
df.head() Density BodyFat Age Weight Height ... Knee Ankle Biceps Forearm Wrist
0 1.0708 12.3 23 154.25 67.75 ... 37.3 21.9 32.0 27.4 17.1
1 1.0853 6.1 22 173.25 72.25 ... 37.3 23.4 30.5 28.9 18.2
2 1.0414 25.3 22 154.00 66.25 ... 38.9 24.0 28.8 25.2 16.6
3 1.0751 10.4 26 184.75 72.25 ... 37.3 22.8 32.4 29.4 18.2
4 1.0340 28.7 24 184.25 71.25 ... 42.2 24.0 32.2 27.7 17.7
[5 rows x 15 columns]Aufgabenteil 1: Datenaufbereitung
Erstelle eine binäre Zielvariable
'Overweight': Diese soll den Wert1haben, wenn derBodyFatgrößer als 25 ist, sonst0.Definiere die Features: Verwende alle numerischen Spalten außer der neu erstellten
Overweight-Variable und der ursprünglichenBodyFat-Variable als Features für die PCA.
Aufgabenteil 2: Principal Component Analysis
Führe eine vollständige PCA auf den standardisierten Features durch und erstelle folgende Visualisierungen:
- Scree Plot: Zeigt die erklärte Varianz pro Hauptkomponente
- Cumulative Explained Variance Plot: Zeigt die kumulative erklärte Varianz mit Linien bei 80% und 95%
- Biplot: Kombiniert Scores (Datenpunkte nach Overweight-Status eingefärbt) und Loadings (als Pfeile) für PC1 vs. PC2
Interpretationsfragen:
- Wie viel Prozent der Gesamtvarianz erklären die ersten 4 Hauptkomponenten zusammen?
- Welche ursprünglichen Features tragen am stärksten zu PC1 bei?
Aufgabenteil 3: kNN-Klassifikation
Vergleiche die Performance von kNN zur Vorhersage des Overweight-Status mit zwei verschiedenen Feature-Sets:
- Original Features: Alle ursprünglichen numerischen Features (standardisiert; außer BodyFat)
- 4 Hauptkomponenten: Die ersten 4 Hauptkomponenten aus der PCA
Experimenteller Aufbau:
- Verwende einen Train-Test Split von 70%/30% mit
random_state=42und Stratifizierung - Verwende Repeated Stratified Cross-Validation mit 5 Folds und 3 Wiederholungen (
random_state=42) - Führe eine Grid Search über folgende k-Werte durch:
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21]
Visualisierung: - Erstelle einen Line Plot, der die Cross-Validation Accuracy für beide Feature-Sets über alle k-Werte zeigt
Zusammenfassung: - Gib eine Übersichtstabelle aus, die für beide Methoden den besten k-Wert, die beste CV-Accuracy und die Test-Accuracy zeigt
Fußnoten
Der Begriff „Scree Plot“ stammt aus der Geologie, wo „scree“ das Geröll am Fuß eines Berges bezeichnet. Raymond Cattell, der diesen Plot 1966 einführte, beschrieb die Abfolge der Eigenwerte als eine Kurve, die zunächst steil abfällt wie ein Berg und dann in eine flachere Phase übergeht, die an ein Geröllfeld erinnert. Die Stelle, an der die Kurve vom steilen Abfall in den flachen Teil übergeht, markiert die Trennung zwischen den wenigen wichtigen Hauptkomponenten und den vielen eher unwichtigen.↩︎
Hauptkomponenten sind immer unkorreliert zueinander – ein großer Vorteil, da wir aus stark korrelierten Features ein neues, sauberes Set an unabhängigen Variablen erhalten.↩︎