import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import LinearSegmentedColormap
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
np.random.seed(42)Klassifikationsgrenzen visualisieren
Wir haben nun zwei verschiedene Klassifikationsmethoden kennengelernt: die logistische Regression und Decision Trees und mit beiden haben wir binäre Klassifikationsprobleme gelöst. Prinzipiell haben wir auch durchgearbeitet wie die beiden Methoden funktionieren, sodass uns auch Unterschiede zwischen Ihnen klar sind.
In diesem Kapitel wollen wir die Gegenüberstellung von Klassifikationsmethoden allerdings noch stärker beleuchten, indem wir für ein ganz spezifisches Datenbeispiel die jeweiligen Klassifikationsergebnisse auf eine nützliche Art und Weise visualisieren.
Das Ergebnis soll prinzipiell etwa so (aber noch besser!) aussehen:
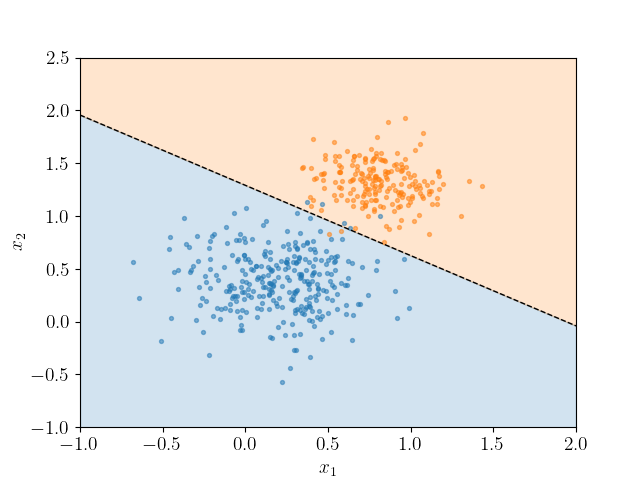
Die Farbe der Punkte gibt an zu welche Klasse sie tatsächlich gehören. Die farbigen Bereiche zeigen, welche Vorhersage das Modell für jeden Punkt treffen würde. Die Grenze zwischen den Farben ist die Klassifikationsgrenze - dort ändert sich die Vorhersage von einer Klasse zur anderen. Diese Art der Visualisierung funktioniert leider nicht für alle Klassifikationsprobleme, auf die ihr jemals stoßen werdet. Tatsächlich funktioniert sie hier nur mit genau zwei numerischen Features - das eine ist auf der x-Achse, das andere auf der y-Achse und die Farbe wird genutzt um die Klassen der zu klassifizierenden Variable (=Label) darzustellen.
Für unser Beispiel verwenden wir wieder die Palmer Penguins, konzentrieren uns nur auf Adelie und Gentoo Pinguine (eine binäre Klassifikation) und nutzen nur zwei numerische Features: body_mass_g und flipper_length_mm.
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
# Nur Gentoo und Adelie Pinguine auswählen
penguins_binary = penguins[penguins['species'].isin(['Gentoo', 'Adelie'])].copy()
penguins_binary = penguins_binary.dropna(subset=['body_mass_g', 'flipper_length_mm'])
print(f"Arten nach Filterung: {penguins_binary['species'].value_counts().to_dict()}")
# Binäre Zielvariable erstellen (0 = Adelie, 1 = Gentoo)
penguins_binary['species_binary'] = (penguins_binary['species'] == 'Gentoo').astype(int)
# Features und Ziel definieren
X = penguins_binary[["body_mass_g", "flipper_length_mm"]].values
y = penguins_binary["species_binary"].values
print(f"Feature-Bereiche:")
print(f" body_mass_g: {X[:, 0].min():.0f} - {X[:, 0].max():.0f} g")
print(f" flipper_length_mm: {X[:, 1].min():.0f} - {X[:, 1].max():.0f} mm")
# Train-Test-Split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)
print(f"Trainingsdaten: {X_train.shape[0]}, Testdaten: {X_test.shape[0]} Pinguine")Arten nach Filterung: {'Adelie': 151, 'Gentoo': 123}
Feature-Bereiche:
body_mass_g: 2850 - 6300 g
flipper_length_mm: 172 - 231 mm
Trainingsdaten: 205, Testdaten: 69 PinguineWir haben also 274 Pinguine (151 Adelie, 123 Gentoo) mit Körpergewichten zwischen 2.850g und 6.300g sowie Flügelspannweiten zwischen 172mm und 231mm.
Die Visualisierungsfunktion
Für die Visualisierung der Klassifikationsgrenzen erstellen wir eine flexible Funktion, die wir für verschiedene Modelle verwenden können. Das Ziel ist nämlich diese Funktion nicht nur in diesem, sondern auch in zukünftigen Kapiteln zu nutzen:
def plot_classifier(model, X_train, y_train, X_test, y_test,
proba=False, xlabel=None, ylabel=None, title=None,
class_colors=None, figsize=(12, 5), axes=None):
"""
Visualisiert Klassifikationsgrenzen für ein trainiertes Modell
Parameter:
- model: Trainiertes sklearn Klassifikationsmodell
- X_train, y_train: Trainingsdaten (Features und Labels)
- X_test, y_test: Testdaten (Features und Labels)
- proba: Bool, ob Wahrscheinlichkeiten (True) oder Klassen (False) gezeigt werden
- xlabel, ylabel: Achsenbeschriftungen
- title: Titel der Abbildung
- class_colors: Dictionary mit Farben für die Klassen {0: 'farbe1', 1: 'farbe2'}
- figsize: Größe der Abbildung als Tuple (width, height)
- axes: Optionales Tupel oder Liste mit zwei matplotlib-Achsenobjekten – wenn angegeben, wird in diese gezeichnet
"""
# Subplot-Layout erstellen: 1 Zeile, 2 Spalten (nur falls keine Achsen übergeben wurden)
if axes is None:
fig, axes = plt.subplots(1, 2, figsize=figsize, sharex=True, sharey=True, layout='tight')
own_fig = True
else:
own_fig = False
# Standard-Farben (Rot & Blau) verwenden, falls keine angegeben
if class_colors is None:
class_colors = {0: 'red', 1: 'blue'}
# Custom Colormap für den Hintergrund erstellen
# Von Klasse 0 (z.B. orange) über weiß zu Klasse 1 (z.B. türkis)
gradient_colors = [class_colors[0], 'white', class_colors[1]]
custom_cmap = LinearSegmentedColormap.from_list("CustomDiverging", gradient_colors, N=256)
# Gemeinsame Grenzen für beide Plots berechnen
# Alle Daten (Training + Test) kombinieren um einheitliche Achsen zu haben
X_all = np.vstack([X_train, X_test])
x_margin = (X_all[:, 0].max() - X_all[:, 0].min()) * 0.05 # 5% Rand
y_margin = (X_all[:, 1].max() - X_all[:, 1].min()) * 0.05 # 5% Rand
x_min = X_all[:, 0].min() - x_margin
x_max = X_all[:, 0].max() + x_margin
y_min = X_all[:, 1].min() - y_margin
y_max = X_all[:, 1].max() + y_margin
# Meshgrid für Hintergrund-Vorhersagen erstellen
# 1000x1000 Grid für glatte Darstellung
xx, yy = np.meshgrid(
np.linspace(x_min, x_max, 1000),
np.linspace(y_min, y_max, 1000)
)
# Vorhersagen für jeden Punkt im Grid
if proba:
# Wahrscheinlichkeiten für Klasse 1
zz = model.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:, 1].reshape(xx.shape)
else:
# Klassenlabels (0 oder 1)
zz = model.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
# Beide Subplots (Training und Test) erstellen
for ax, X, y, subset in zip(axes, [X_train, X_test], [y_train, y_test],
["Trainingsdaten", "Testdaten"]):
# Vorhersagen für die aktuellen Daten
y_pred = model.predict(X)
# Hintergrund mit Klassifikationsgrenzen zeichnen
if proba:
# Kontinuierliche Wahrscheinlichkeiten als Heatmap
ax.imshow(zz, origin="lower", aspect="auto",
extent=(x_min, x_max, y_min, y_max),
vmin=0, vmax=1, alpha=0.25, cmap=custom_cmap);
else:
# Diskrete Klassengrenzen
ax.contourf(xx, yy, zz,
alpha=0.25,
vmin=0, vmax=1,
levels=[-0.5, 0.5, 1.5], # Grenzen für Klasse 0 und 1
colors=[class_colors[0], class_colors[1]]);
# Datenpunkte zeichnen
# Gesichtsfarbe basiert auf wahrer Klasse
face_colors = [class_colors[int(label)] for label in y]
# Randfarbe zeigt richtige (schwarz) vs. falsche (rot) Vorhersagen
edge_colors = ['black' if true_label == pred_label else 'red'
for true_label, pred_label in zip(y, y_pred)]
ax.scatter(X[:, 0], X[:, 1],
c=face_colors,
edgecolor=edge_colors,
linewidth=1,
s=50);
# Subplot-Eigenschaften setzen
ax.set_title(subset);
ax.set_xlim(x_min, x_max);
ax.set_ylim(y_min, y_max);
if xlabel:
ax.set_xlabel(xlabel);
if ylabel:
ax.set_ylabel(ylabel);
# Gesamttitel und Anzeige nur, wenn eigene Figure erzeugt wurde
if own_fig:
if title:
fig.suptitle(title, fontsize=14);
plt.show()Etwas mehr Erläuterungen zur Funktion folgen gleich unten, nachdem wir sie erstmals angewendet haben.
Logistische Regression visualisieren
Beginnen wir mit der logistischen Regression. Wie wir in Kapitel 5.1 gelernt haben, nutzt sie eine sigmoidale Funktion, um Wahrscheinlichkeiten zu berechnen.
# Logistische Regression trainieren
logreg = LogisticRegression(random_state=42)
logreg.fit(X_train, y_train);
# Parameter der logistischen Regression ausgeben
print(f"Intercept: {logreg.intercept_[0]:.4f}")
print(f"Koeffizient body_mass_g: {logreg.coef_[0][0]:.4f}")
print(f"Koeffizient flipper_length_mm: {logreg.coef_[0][1]:.4f}")
# Performance checken
y_pred_train = logreg.predict(X_train)
y_pred_test = logreg.predict(X_test)
print(f"Logistische Regression:")
print(f" Training Accuracy: {accuracy_score(y_train, y_pred_train):.3f}")
print(f" Test Accuracy: {accuracy_score(y_test, y_pred_test):.3f}")Intercept: -204.8625
Koeffizient body_mass_g: 0.0045
Koeffizient flipper_length_mm: 0.8971
Logistische Regression:
Training Accuracy: 0.985
Test Accuracy: 0.986Erstaunlich: 98,5% Accuracy auf den Trainingsdaten und 98,6% auf den Testdaten! Das zeigt, dass unsere beiden Features sehr gut zwischen Adelie und Gentoo Pinguinen unterscheiden können.
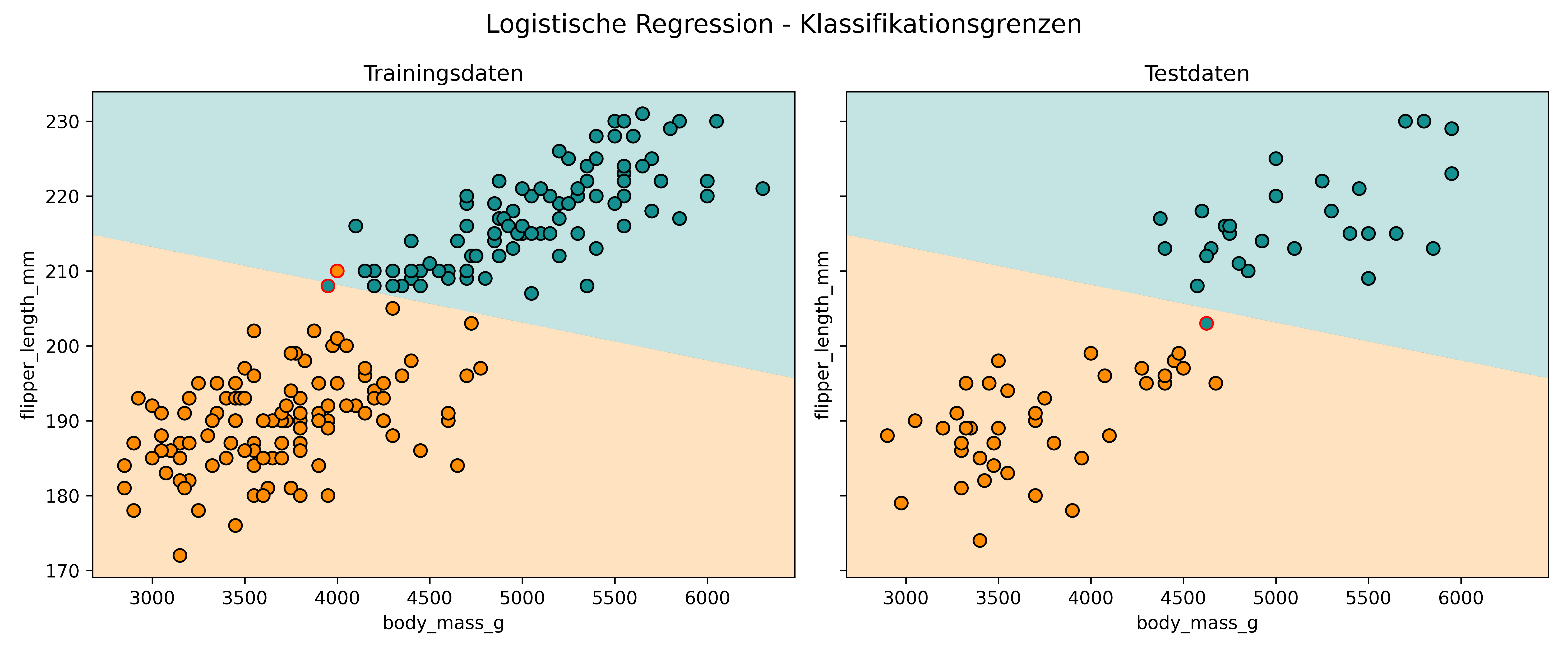
Schauen wir uns zuerst die scharfen Klassifikationsgrenzen an:
# Klassifikationsgrenzen visualisieren
plot_classifier(
model=logreg,
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
proba=False,
title="Logistische Regression - Klassifikationsgrenzen",
xlabel="body_mass_g",
ylabel="flipper_length_mm",
class_colors={0: colors['Adelie'], 1: colors['Gentoo']}
)
Diese Funktion plot_classifier() braucht also mindestens 5 Dinge:
- Ein trainiertes sklearn-Modell (
model) - mit genau zwei numerischen Features und einem binären Label. - Trainingsdaten (
X_train,y_train) - Testdaten (
X_test,y_test)
All diese Dinge hat man sowieso, wenn man ein Klassifikationsproblem mit sklearn angeht. Darüber hinaus hat die Funktion außerdem optionale Parameter:
-
proba: Ein boolescher Wert, der angibt, ob die Vorhersagen als Wahrscheinlichkeiten (True) oder als Klassenlabels (False) dargestellt werden sollen. -
xlabel,ylabel: Beschriftungen für die Achsen -
title: Titel der Abbildung -
class_colors: Dictionary mit Farben für die Klassen{0: 'farbe1', 1: 'farbe2'} -
figsize: Größe der Abbildung als Tuple(width, height) -
axes: Wird benötigt, falls man mehrere solcher Abbildungen kombinieren will - siehe Abschnitt Methodenvergleich unten.
In jedem Fall erzeugt die Funktion ein Gitter über den gesamten Merkmalsraum - also systematisch verteilte Punkte für alle Kombinationen der relevanten x- und y-Werte. Für all diese Punkte wird dann vom Modell eine Vorhersage zur Klassifikation getroffen, sodass damit die gesamte Fläche des Plots entsprechend eingefärbt werden kann.
Die Datenpunkte werden schließlich darüber gezeichnet. Die Füllfarbe eines jeden Punkts entspricht der tatsächlichen Klasse, wobei jeder Punkt, der laut Modell falsch klassifiziert wurde, einen roten Rand erhält.
Besonders praktisch ist der Parameter proba: Bei False sehen wir scharfe Klassifikationsgrenzen, bei True kontinuierliche Wahrscheinlichkeitsübergänge.
Schließlich sehen wir das ganze direkt zwei Mal: Einmal für die Trainingsdaten und einmal für die Testdaten.
Die Idee eine solche Funktion zu nutzen um über verschiedene Klassifikationsmethoden zu visualisieren stammt aus dem Udemy Kurs Machine Learning von A-Z: Lerne Python & R für Data Science! von Jannis Seemann. Die Funktion hier ist also eine Erweiterung der dort gezeigten Funktion.
Die logistische Regression zieht eine glatte zwischen den beiden Klassen. Alles oberhalb/rechts der Linie wird als Gentoo klassifiziert (türkis), alles unterhalb/links als Adelie (orange).
Jetzt setzen wir mal proba=True und schauen uns die Wahrscheinlichkeiten, also eine kontinuierliche Klassifikationsgrenze an:
plot_classifier(
model=logreg,
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
proba=True,
title="Logistische Regression - Wahrscheinlichkeiten",
xlabel="body_mass_g",
ylabel="flipper_length_mm",
class_colors={0: colors['Adelie'], 1: colors['Gentoo']}
)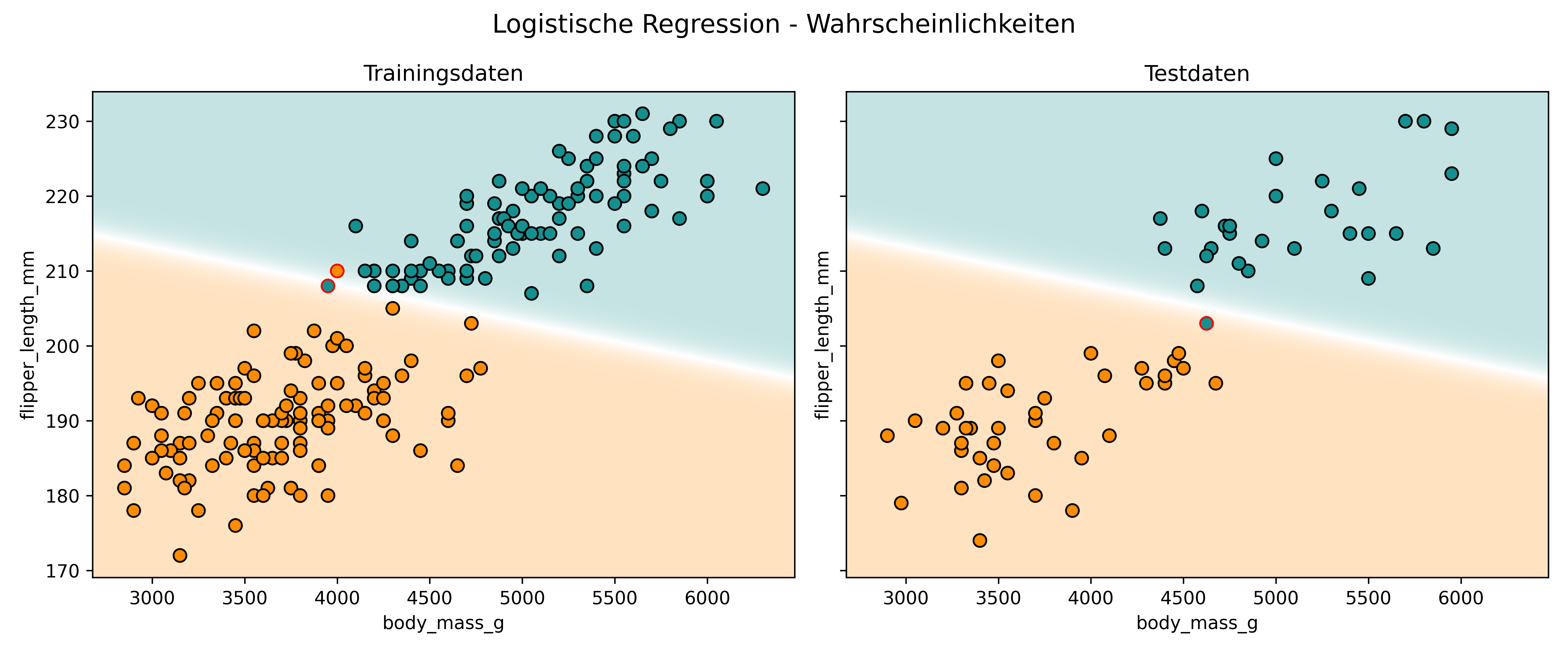
Hier sehen wir den kontinuierlichen Übergang: Orange bedeutet hohe Wahrscheinlichkeit für Adelie, türkis hohe Wahrscheinlichkeit für Gentoo, und weiß bedeutet etwa 50:50. Die sigmoidale Natur der logistischen Regression sorgt für diese glatten Übergänge.
3D-Exkurs: Die Wahrscheinlichkeitsfläche
Um noch besser zu verstehen, was unsere 2D-Darstellung hier eigentlich zeigt, machen wir einen kurzen Ausflug in die dritte Dimension. In vergangenen Kapiteln mit genau einem numerischen Feature und der logistische Regression hatten wir ja sigmoide Kurven gezeichnet, wobei das Feature auf der x-Achse und die Wahrscheinlichkeit auf der y-Achse war. Um das klarzustellen: Auch bei unseren jetzigen zwei numerischen Features gibt es diese sigmoiden Kurven, aber eben pro Feature. Wenn wir diese zwei Dimensionen gemeinsam darstellen wollen, können wir das wie folgt tun:
Code zeigen/verstecken
# Grid für 3D-Darstellung erstellen
mass_min, mass_max = X[:, 0].min(), X[:, 0].max()
flipper_min, flipper_max = X[:, 1].min(), X[:, 1].max()
mass_range = np.linspace(mass_min, mass_max, 50)
flipper_range = np.linspace(flipper_min, flipper_max, 50)
mass_grid, flipper_grid = np.meshgrid(mass_range, flipper_range)
# Wahrscheinlichkeiten für das Grid berechnen
grid_points = np.c_[mass_grid.ravel(), flipper_grid.ravel()]
z_proba = logreg.predict_proba(grid_points)[:, 1] # Wahrscheinlichkeit für Gentoo
z_grid = z_proba.reshape(mass_grid.shape)
# Custom Colormap
gradient_colors = [colors['Adelie'], 'white', colors['Gentoo']]
custom_cmap = LinearSegmentedColormap.from_list("CustomDiverging", gradient_colors, N=256)
# 3D-Plot erstellen
fig = plt.figure(figsize=(14, 10))
# Zwei Blickwinkel nebeneinander
ax1 = fig.add_subplot(121, projection='3d')
ax2 = fig.add_subplot(122, projection='3d')
for ax, elev, azim, subtitle in [(ax1, 30, 160, "Seitenansicht"),
(ax2, 90, 180, "Draufsicht")]:
# Datenpunkte (bei Z-Werten 0 oder 1)
ax.scatter(
penguins_binary['flipper_length_mm'],
penguins_binary['body_mass_g'],
penguins_binary['species_binary'],
c=penguins_binary['species'].map(colors),
marker='o', alpha=0.8, s=50
);
# Modellfläche
ax.plot_surface(
flipper_grid, mass_grid, z_grid,
cmap=custom_cmap,
alpha=0.6,
linewidth=0,
antialiased=True
);
ax.set_xlabel('flipper_length_mm');
ax.set_ylabel('body_mass_g');
ax.set_zlabel('Wahrscheinlichkeit (Gentoo)');
ax.set_title(f'Logistische Regression - {subtitle}');
ax.view_init(elev=elev, azim=azim);
plt.tight_layout();
plt.show()
print(f"Wahrscheinlichkeitsbereich: {z_proba.min():.3f} - {z_proba.max():.3f}")
print(f"Anzahl unterschiedliche Wahrscheinlichkeitswerte: {len(np.unique(np.round(z_proba, 3)))}")
Wahrscheinlichkeitsbereich: 0.000 - 1.000
Anzahl unterschiedliche Wahrscheinlichkeitswerte: 350Die 3D-Darstellung zeigt eine geschwungene Fläche - die sigmoidale Oberfläche. Sie entsteht, wenn zwei sigmoide Kurven orthogonal zueinander laufen. Drehen wir diese 3D-Visualisierung nun so, dass wir eine Draufsicht erhalten, so entspricht das exakt unserer 2D-Visualisierung bei proba=true: Wir schauen von oben auf diese Fläche und färben die Bereiche entsprechend der Höhe (Wahrscheinlichkeit).
Decision Tree hinzufügen
Jetzt wenden wir unsere Visualisierungsfunktion auf Decision Trees an:
# Decision Tree trainieren
tree = DecisionTreeClassifier(max_depth=4, random_state=42)
tree.fit(X_train, y_train);
# Baumstruktur visualisieren
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
plot_tree(tree,
feature_names=['body_mass_g', 'flipper_length_mm'],
class_names=['Adelie', 'Gentoo'],
filled=True,
rounded=True,
ax=ax)
plt.show()
# Performance checken
y_pred_tree_train = tree.predict(X_train)
y_pred_tree_test = tree.predict(X_test)
print(f"Decision Tree:")
print(f" Training Accuracy: {accuracy_score(y_train, y_pred_tree_train):.3f}")
print(f" Test Accuracy: {accuracy_score(y_test, y_pred_tree_test):.3f}")
print(f" Baumtiefe: {tree.get_depth()}")
print(f" Anzahl Blätter: {tree.get_n_leaves()}")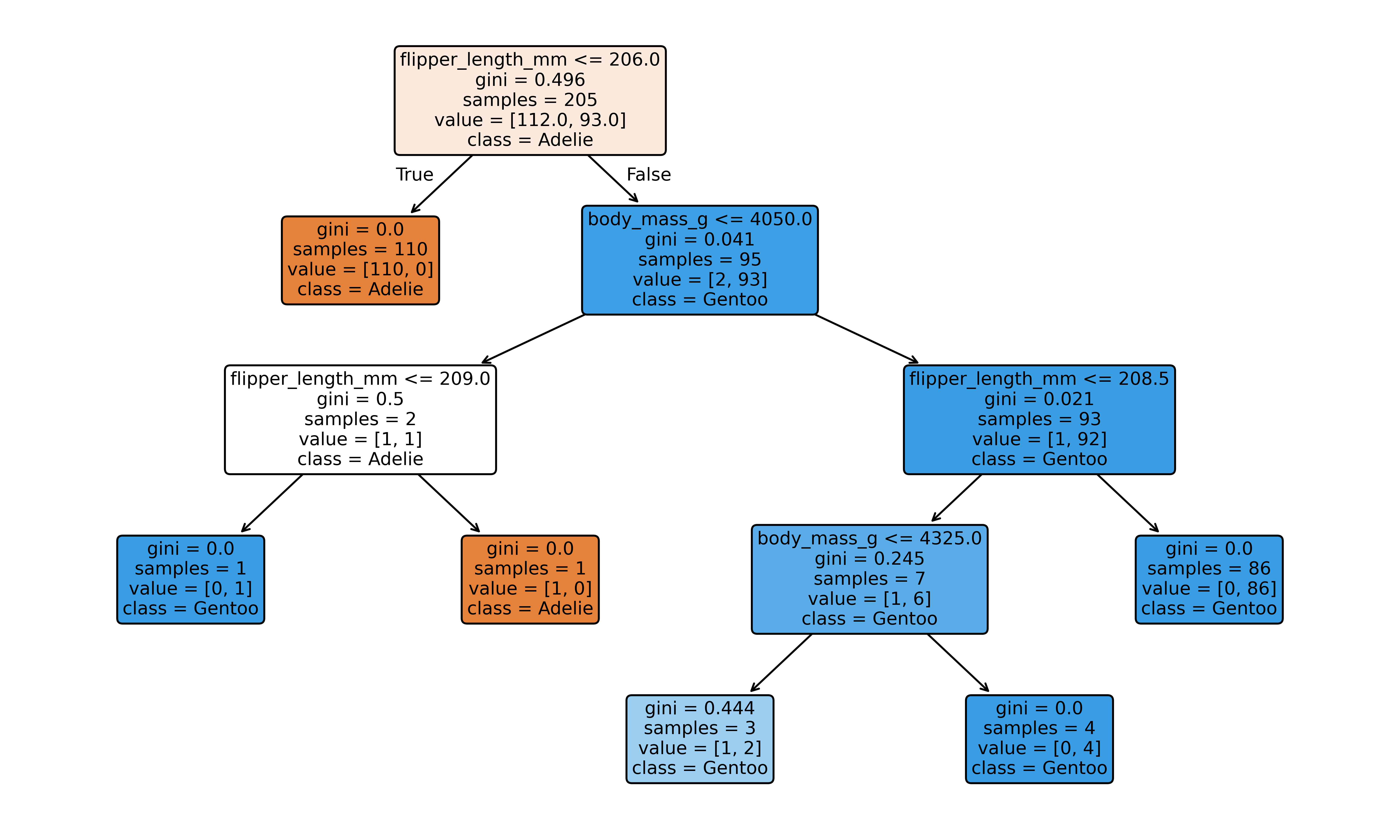
Decision Tree:
Training Accuracy: 0.995
Test Accuracy: 0.986
Baumtiefe: 4
Anzahl Blätter: 6Interessant: 99,5% Accuracy beim Training, aber die gleichen 98,6% beim Test wie die logistische Regression. Der Baum ist 4 Stufen tief und hat 6 Endknoten.
plot_classifier(
model=tree,
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
proba=False,
title="Decision Tree - Klassifikationsgrenzen",
xlabel="body_mass_g",
ylabel="flipper_length_mm",
class_colors={0: colors['Adelie'], 1: colors['Gentoo']}
)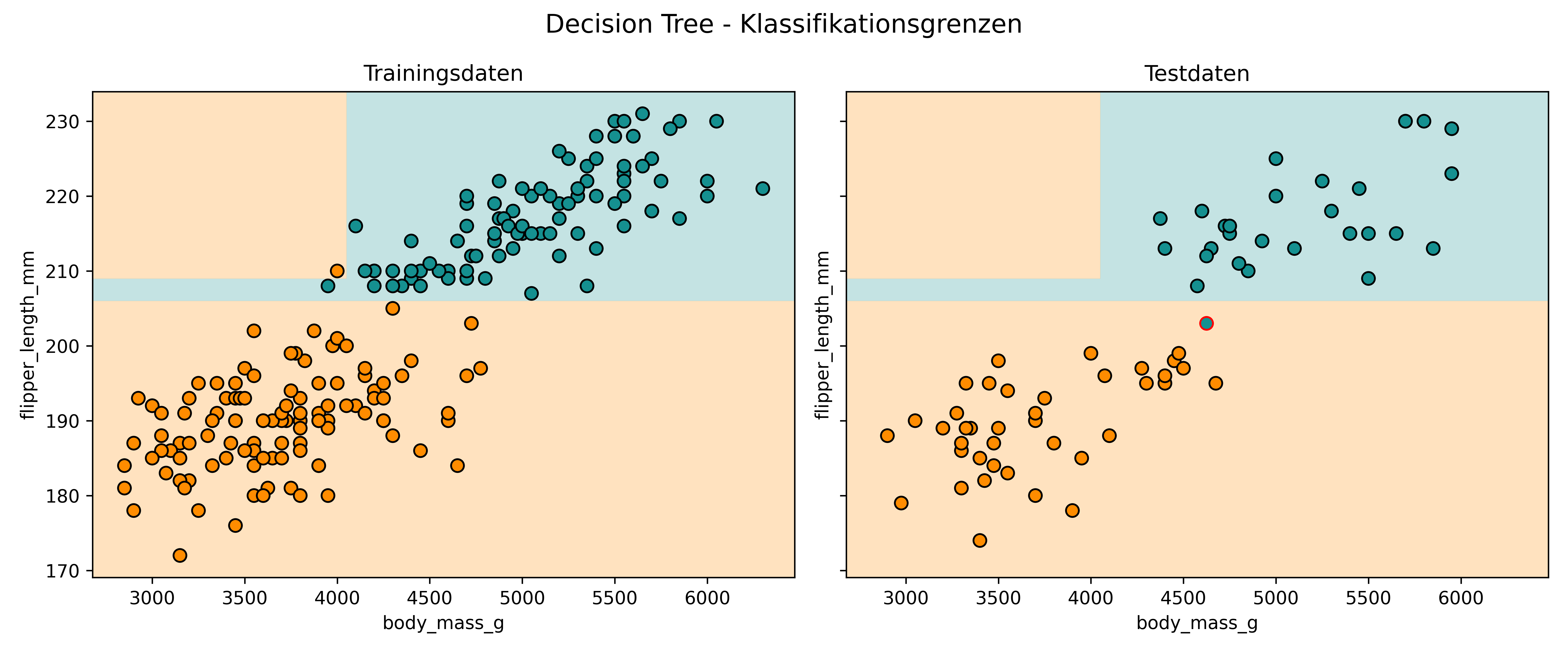
Hier sehen wir den fundamentalen Unterschied: Decision Trees erstellen rechteckige Bereiche mit Kanten, die stets orthogonal zur Achse des Features stehen. Das liegt daran, dass jede Entscheidung im Baum eine einfache Regel wie “body_mass_g > 4000” ist - also hier immer horizontale oder vertikale Trennlinien.
plot_classifier(
model=tree,
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
proba=True,
title="Decision Tree - Wahrscheinlichkeiten",
xlabel="body_mass_g",
ylabel="flipper_length_mm",
class_colors={0: colors['Adelie'], 1: colors['Gentoo']}
)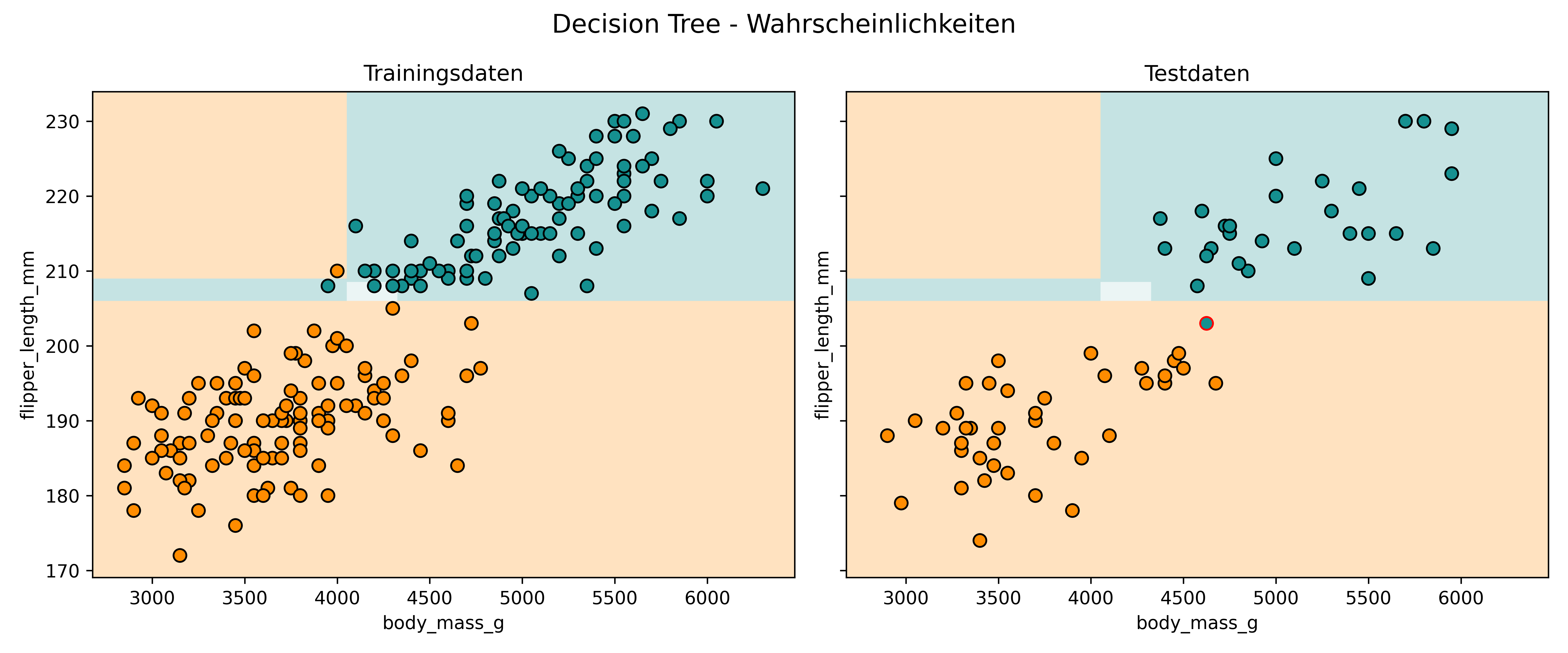
Auch bei proba=True sehen wir rechteckige Bereiche mit scharfen Übergängen. Das liegt daran, dass ein Decision Tree keine kontinuierliche Wahrscheinlichkeitsfunktion wie die logistische Regression lernt, sondern diskrete Regeln verwendet. Der Begriff proba (kurz für probability) kann hier daher leicht in die Irre führen.
Tatsächlich heißt das Argument proba, weil in diesem Fall intern die Methode predict_proba() des sklearn-Modells aufgerufen wird (statt sonst predict()). Bei einem Decision Tree bedeutet predict_proba() jedoch nicht, dass eine modellierte Wahrscheinlichkeit berechnet wird. Stattdessen wird einfach der Anteil der Trainingspunkte der Zielklasse im jeweiligen Blatt zurückgegeben, in dem ein Punkt landet.
Mit anderen Worten: predict_proba() gibt bei Decision Trees eine empirische relative Häufigkeit an – also eine Art Durchschnitt darüber, wie oft diese Klasse unter ähnlichen (Trainings-)Punkten vorkam. Man sollte sie daher nicht im selben Sinn wie bei der logistischen Regression als “wahre” Wahrscheinlichkeiten interpretieren. Trotzdem sind sie das Nächstliegende zu Wahrscheinlichkeiten, was ein Decision Tree liefern kann – deshalb wird diese Information von sklearn über predict_proba() bereitgestellt.
Wir können uns auch hier an eine 3D-Ansicht wagen:
Code zeigen/verstecken
z_proba_tree = tree.predict_proba(grid_points)[:, 1]
z_grid_tree = z_proba_tree.reshape(mass_grid.shape)
fig = plt.figure(figsize=(14, 10))
ax1 = fig.add_subplot(121, projection='3d')
ax2 = fig.add_subplot(122, projection='3d')
for ax, elev, azim, subtitle in [(ax1, 30, 160, "Seitenansicht"),
(ax2, 90, 180, "Draufsicht")]:
# Datenpunkte
ax.scatter(
penguins_binary['flipper_length_mm'],
penguins_binary['body_mass_g'],
penguins_binary['species_binary'],
c=penguins_binary['species'].map(colors),
marker='o', alpha=0.8, s=50
);
# Modellfläche (bewusst ohne antialiasing für scharfe Kanten)
ax.plot_surface(
flipper_grid, mass_grid, z_grid_tree,
cmap=custom_cmap,
alpha=0.6,
linewidth=0,
antialiased=False
);
ax.set_xlabel('flipper_length_mm');
ax.set_ylabel('body_mass_g');
ax.set_zlabel('Wahrscheinlichkeit (Gentoo)');
ax.set_title(f'Decision Tree - {subtitle}');
ax.view_init(elev=elev, azim=azim);
plt.tight_layout()
plt.show()
unique_probs = np.unique(np.round(z_proba_tree, 3))
print(f"Wahrscheinlichkeitswerte Decision Tree: {unique_probs}")
print(f"Anzahl verschiedene Werte: {len(unique_probs)}")
Wahrscheinlichkeitswerte Decision Tree: [0. 0.667 1. ]
Anzahl verschiedene Werte: 3Die Decision Tree 3D-Fläche sieht aus wie eine Treppenfläche mit abrupten Sprüngen! Im Gegensatz zur logistischen Regression gibt es nur 3 verschiedene Wahrscheinlichkeitswerte: [0.000, 0.667, 1.000]. Das spiegelt die diskrete Natur der Baumvorhersagen wider.
Methodenvergleich: Konzeptionelle Unterschiede
Jetzt können wir die beiden Methoden direkt nebeneinander betrachten:
fig, axes = plt.subplots(2, 2, figsize=(14, 10), layout='tight', sharex=True, sharey=True)
axes = axes.flatten()
# Logistische Regression – linke zwei Achsen
plot_classifier(
model=logreg,
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
proba=True,
xlabel="body_mass_g",
ylabel="flipper_length_mm",
class_colors={0: colors['Adelie'], 1: colors['Gentoo']},
axes=axes[0:2]
)
# Decision Tree – rechte zwei Achsen
plot_classifier(
model=tree,
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
proba=True,
xlabel="body_mass_g",
ylabel="flipper_length_mm",
class_colors={0: colors['Adelie'], 1: colors['Gentoo']},
axes=axes[2:4]
)
fig.suptitle("Logistische Regression (oben) vs. Decision Tree (unten)", fontsize=16)
plt.show()
# Fehlklassifikationen analysieren
errors_logreg = np.sum(y_test != y_pred_test)
errors_tree = np.sum(y_test != y_pred_tree_test)
print(f"Fehlklassifizierte Punkte im Test-Set:")
print(f" Logistische Regression: {errors_logreg}/{len(y_test)} ({errors_logreg/len(y_test)*100:.1f}%)")
print(f" Decision Tree: {errors_tree}/{len(y_test)} ({errors_tree/len(y_test)*100:.1f}%)")
Fehlklassifizierte Punkte im Test-Set:
Logistische Regression: 1/69 (1.4%)
Decision Tree: 1/69 (1.4%)Die Visualisierung macht die konzeptionellen Unterschiede deutlich1:
Logistische Regression erstellt eine beliebig rotierbare Klassifikationsgrenze mit kontinuierlichen Wahrscheinlichkeiten und sanften Übergängen.
Decision Trees erstellen rechteckige Bereiche durch aufeinanderfolgende binäre Entscheidungen, also scharfen, horizontalen oder vertikalen Kanten.
Beide Modelle zeigen hier identische Test-Performance (98,6% mit nur je einem Fehler - und zwar sogar für denselben Datenpunkt), aber ihre “Denkweise” ist fundamental unterschiedlich.
Ausblick: Ein Template für die Zukunft
Diese Visualisierungstechnik werden wir in kommenden Kapiteln immer wieder verwenden um auch die nächsten Klassifikationsmethoden zu vergleichen. Die plot_classifier() Funktion funktioniert für alle sklearn Modelle - ihr könnt sie euch also schon mal abspeichern.
Der Spezialfall mit genau zwei numerischen Features ist zwar in der Praxis selten, aber didaktisch wertvoll. Er hilft uns zu verstehen, wie verschiedene Algorithmen an das gleiche Problem herangehen. Diese Intuition ist auch bei höherdimensionalen Problemen hilfreich, auch wenn wir sie dann nicht mehr auf diese Weise visualisieren können.
Übungen
Nochmal, aber für andere Features
Führe denselben Methodenvergleich wie im Kapitel durch, aber mit den Features bill_length_mm und body_mass_g. Kopiere die plot_classifier() Funktion aus dem Kapitel und implementiere dann den kompletten Workflow: Daten vorbereiten (Adelie und Gentoo filtern, fehlende Werte entfernen, binäre Zielvariable erstellen), Train-Test-Split mit test_size=0.25, beide Modelle trainieren (logistische Regression und Decision Tree mit max_depth=4), Performance bewerten und schließlich die 2×2 Subplot-Visualisierung mit proba=True und passenden Achsenbeschriftungen erstellen (wie im Abschnitt Methodenvergleich).
Analysiere die Ergebnisse: Wie unterscheiden sich die Klassifikationsgrenzen bei dieser Feature-Kombination im Vergleich zu body_mass_g vs flipper_length_mm?
Fußnoten
Nochmal der Hinweis, dass einige von diesen Aussagen nur für diesen speziellen Fall mit zwei numerischen Features und einem binären Label gilt.↩︎