import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats
from scipy.stats import levene
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.stats.diagnostic import het_breuschpagan
from statsmodels.stats.stattools import jarque_bera
from statsmodels.graphics.gofplots import qqplot
import seaborn as sns
np.random.seed(42) # für reproduzierbare ErgebnisseModelldiagnostik und Residuenanalyse
Warum Modelldiagnostik wichtig ist
Die statistische Modellierung ist ein mächtiges Werkzeug, um Zusammenhänge in Daten zu verstehen und daraus Schlüsse zu ziehen. Allerdings basieren alle statistischen Modelle auf bestimmten Annahmen. Wenn diese Annahmen verletzt werden, können die Ergebnisse und Schlussfolgerungen irreführend oder sogar falsch sein.
Deshalb ist die Modelldiagnostik ein entscheidender Schritt in der statistischen Analyse. Sie hilft uns zu verstehen, ob unsere Modelle die Daten angemessen beschreiben und ob die Annahmen, die wir treffen, gerechtfertigt sind. In diesem Kapitel werden wir verschiedene Methoden der Modelldiagnostik kennenlernen, mit besonderem Fokus auf die Überprüfung der Annahmen linearer Modelle.
Die Annahmen linearer Modelle
Bevor wir mit der Diagnose beginnen, sollten wir verstehen, welche Annahmen lineare Modelle (einschließlich linearer Regression und ANOVA) treffen. Diese Annahmen können unter dem Akronym “LINE” zusammengefasst werden:
- Linearity (Linearität): Die Beziehung zwischen den Prädiktoren und der Zielvariable ist linear.
- Independenz (Unabhängigkeit): Die Beobachtungen sind voneinander unabhängig.
- Normality (Normalverteilung): Die Residuen (Fehler) sind normalverteilt.
- Equal Variance (Varianzhomogenität): Die Varianz der Residuen ist konstant über alle Werte der Prädiktoren.
Es gilt also prinzipiell immer zu prüfen, ob es gerechtfertigt ist , ein lineares Modell zu verwenden. Wenn wir nämlich z.B. offensichtlich nicht normalverteilte Residuen haben, ist es nicht sinnvoll, ein lineares Modell zu verwenden. Solch eine Prüfung geschieht in der Regel durch eine Kombination aus grafischen und statistischen Tests - wie in den folgenden Abschnitten gezeigt.
Interessanterweise wird die Linearitätsannahme bei verschiedenen statistischen Modellen unterschiedlich gehandhabt:
| Aspekt | Einfache lineare Regression | Multiple lineare Regression | Polynomregression | ANOVA |
|---|---|---|---|---|
| Linearität in Parametern | Ja | Ja | Ja | Ja |
| Linearität in Variablen | Ja (empirisch zu prüfen) | Ja (empirisch zu prüfen) | Nein (bewusst nicht-linear) | Nicht relevant (kategorisch) |
| Typische Prüfungen | Residualanalyse, Streudiagramm | Partielle Residualplots, Streudiagrammatrix | - | - |
Bei ANOVA ist die Linearitätsannahme in Bezug auf Variablen nicht relevant, da wir mit kategorialen Prädiktoren arbeiten und lediglich Gruppenmittelwerte vergleichen. Deshalb konzentrieren sich ANOVA-Diagnosen hauptsächlich auf Varianzhomogenität und Normalverteilung.
Bei der einfachen und multiplen linearen Regression müssen wir hingegen prüfen, ob die Beziehung zwischen den einzelnen Prädiktoren und der Zielvariable tatsächlich linear ist. Dies ist ein wesentlicher Teil der Diagnose.
Die Polynomregression ist zwar linear in den Parametern (wie alle genannten Modelle), modelliert aber bewusst nicht-lineare Beziehungen in den Variablen durch Hinzufügen transformierter Terme (x², x³, etc.). Die Linearitätsprüfung für die ursprüngliche x-y-Beziehung entfällt, stattdessen prüfen wir, ob die gewählte Polynomordnung die Datenstruktur angemessen abbildet.
Modellbeispiele laden
Für unsere Diagnostik verwenden wir den Palmer Penguins Datensatz und erstellen daraus zwei verschiedene Modelle. In beiden Fällen ist body_mass_g die Zielvariable, die wir vorhersagen möchten. Wir verwenden flipper_length_mm als Prädiktor für das lineare Regressionsmodell und species für das ANOVA-Modell.
# Palmer Penguins Datensatz laden und reduzieren
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
penguins_clean = penguins[['body_mass_g', 'flipper_length_mm', 'species']].dropna()
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
Lineares Regressionsmodell
Hier fokussieren wir uns auf die zwei Variablen flipper_length_mm und body_mass_g.
# Lineares Regressionsmodell
lm_model = smf.ols(formula='body_mass_g ~ flipper_length_mm', data=penguins_clean).fit()
# Visualisierung des Modells mit Regressionsgerade
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
ax.scatter(penguins_clean['flipper_length_mm'], penguins_clean['body_mass_g'], alpha=0.7)
# Regressionsgerade hinzufügen
x_range = np.linspace(penguins_clean['flipper_length_mm'].min(),
penguins_clean['flipper_length_mm'].max(), 100)
y_pred = lm_model.params[0] + lm_model.params[1] * x_range
ax.plot(x_range, y_pred, color='red', linestyle='-', linewidth=2)
ax.set_xlabel('Flossenlänge (mm)')
ax.set_ylabel('Körpergewicht (g)')
ax.set_title('Lineares Regressionsmodell: Körpergewicht ~ Flossenlänge')
plt.show()
print(lm_model.summary())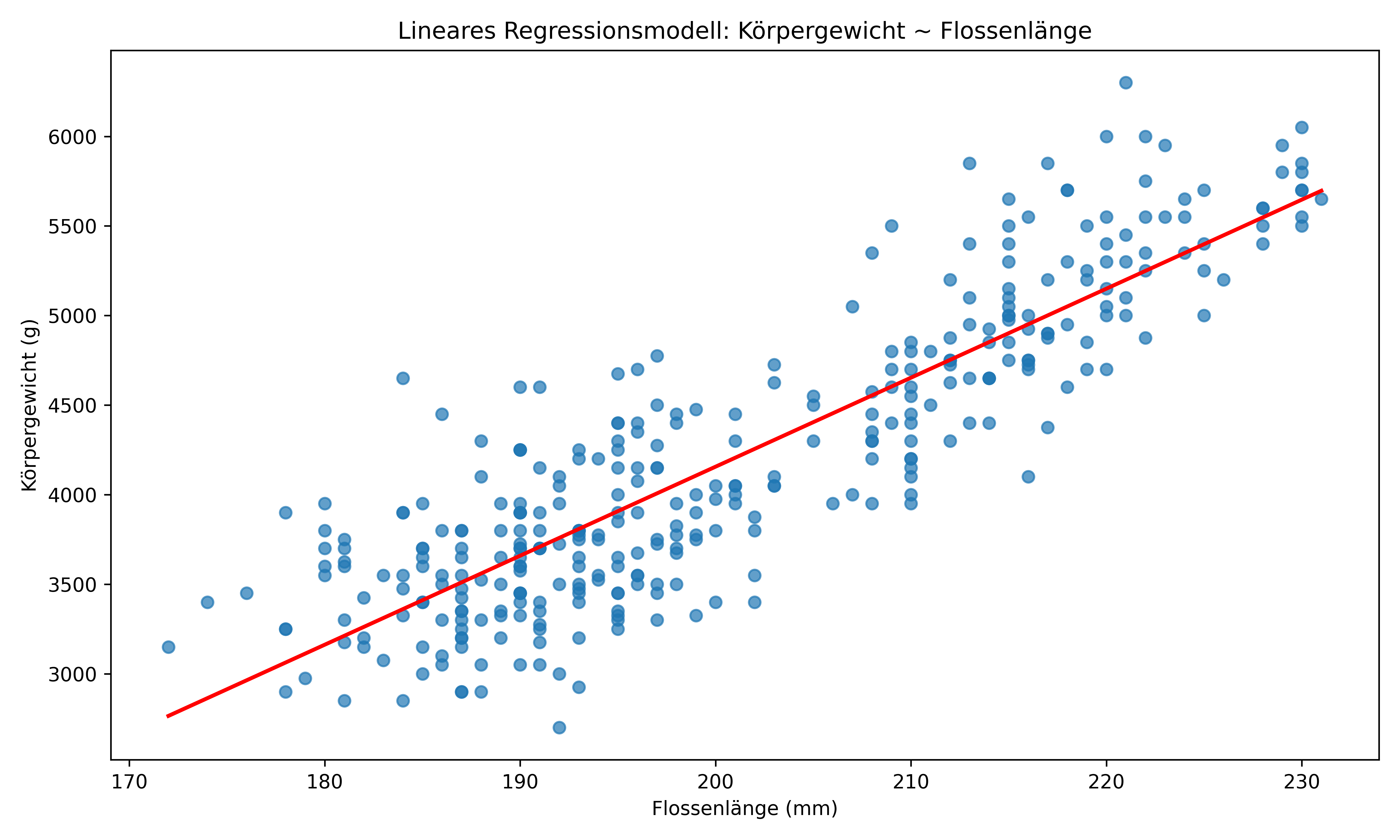
OLS Regression Results
==============================================================================
Dep. Variable: body_mass_g R-squared: 0.759
Model: OLS Adj. R-squared: 0.758
Method: Least Squares F-statistic: 1071.
Date: Di, 19 Aug 2025 Prob (F-statistic): 4.37e-107
Time: 11:41:24 Log-Likelihood: -2528.4
No. Observations: 342 AIC: 5061.
Df Residuals: 340 BIC: 5069.
Df Model: 1
Covariance Type: nonrobust
=====================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------
Intercept -5780.8314 305.815 -18.903 0.000 -6382.358 -5179.305
flipper_length_mm 49.6856 1.518 32.722 0.000 46.699 52.672
==============================================================================
Omnibus: 5.634 Durbin-Watson: 2.190
Prob(Omnibus): 0.060 Jarque-Bera (JB): 5.585
Skew: 0.313 Prob(JB): 0.0613
Kurtosis: 3.019 Cond. No. 2.89e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.89e+03. This might indicate that there are
strong multicollinearity or other numerical problems.ANOVA-Modell
Hier fokussieren wir uns wieder auf die zwei Variablen species und body_mass_g.
Code zeigen/verstecken
# Funktion aus dem letzten Kapitel wiederverwenden
def plot_species(df, species_list, ref_value=None):
"""
Erstellt einen Jitter-Plot des Körpergewichts (body_mass_g) für eine oder mehrere Pinguinarten.
"""
# Plot-Setup
fig, ax = plt.subplots(figsize=(7, 4), layout='tight')
# Filtere nur relevante Arten und entferne NA-Werte in 'body_mass_g'
df_plot = df[df['species'].isin(species_list)].dropna(subset=['body_mass_g'])
# x-Positionen auf der Achse für jede Art
x_positions = {sp: i for i, sp in enumerate(species_list)}
# Durchlaufe alle gewünschten Arten
for species in species_list:
# Wähle Daten für die aktuelle Art
data = df_plot[df_plot['species'] == species]['body_mass_g']
# Erzeuge leicht gestreute x-Werte (Jitter), damit sich Punkte nicht überlappen
x_jitter = np.random.normal(loc=x_positions[species], scale=0.05, size=len(data))
# Streudiagramm der Einzelbeobachtungen
ax.scatter(x_jitter, data, alpha=0.7, s=20, color=colors[species])
# Berechne und plotte den Mittelwert als gestrichelte Linie
mean_val = data.mean()
ax.hlines(y=mean_val, xmin=x_positions[species]-0.2, xmax=x_positions[species]+0.2,
colors="black", linestyles='--', linewidth=2)
# Textbeschriftung für den Mittelwert
ax.text(x_positions[species]+0.25, mean_val, f"{mean_val:.0f} g",
va='center', ha='left', fontsize=9, color=colors[species])
# Optional: Referenzwert für Ein-Stichproben-Test (nur bei einer Art)
if ref_value is not None and len(species_list) == 1:
ax.hlines(y=ref_value, xmin=-0.2, xmax=0.2, colors='red', linestyles='-', linewidth=2)
ax.text(0.25, ref_value, f"{ref_value} g (Referenzwert)", va='center', ha='left',
fontsize=9, color='red')
# Achsenbeschriftungen und kosmetische Einstellungen
ax.set_ylabel('Körpergewicht (g)')
ax.set_xticks(list(x_positions.values()))
ax.set_xticklabels(species_list)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# Plot anzeigen
plt.show()# Alle drei Pinguinarten vergleichen
plot_species(penguins, ['Adelie', 'Chinstrap', 'Gentoo'])
# ANOVA-Modell
anova_model = smf.ols('body_mass_g ~ C(species)', data=penguins_clean).fit()
print(anova_model.summary())
# ANOVA-Tabelle
anova_table = sm.stats.anova_lm(anova_model, typ=2)
print("\nANOVA-Tabelle:")
print(anova_table)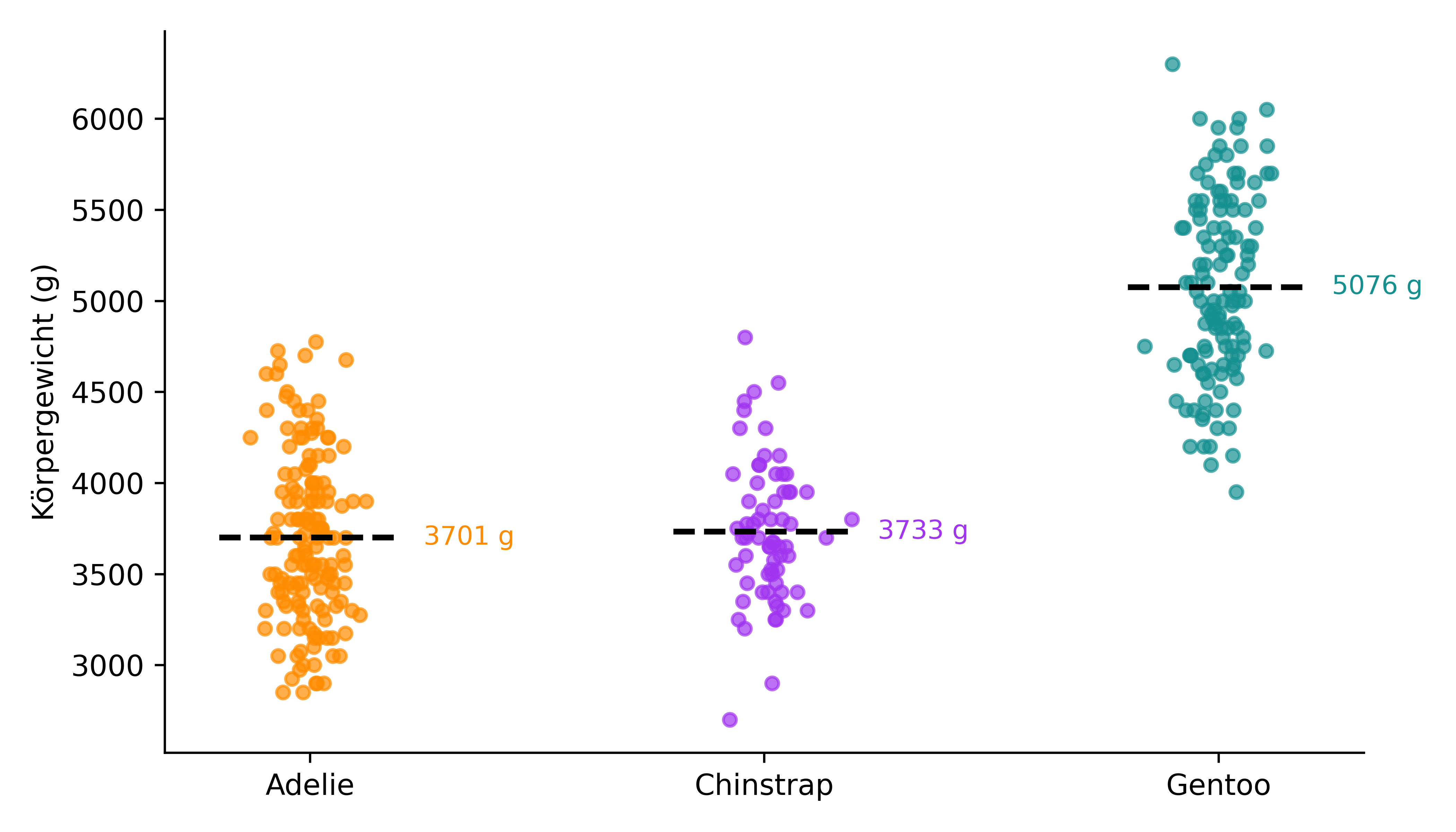
OLS Regression Results
==============================================================================
Dep. Variable: body_mass_g R-squared: 0.670
Model: OLS Adj. R-squared: 0.668
Method: Least Squares F-statistic: 343.6
Date: Di, 19 Aug 2025 Prob (F-statistic): 2.89e-82
Time: 11:41:24 Log-Likelihood: -2582.3
No. Observations: 342 AIC: 5171.
Df Residuals: 339 BIC: 5182.
Df Model: 2
Covariance Type: nonrobust
===========================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------------
Intercept 3700.6623 37.619 98.371 0.000 3626.665 3774.659
C(species)[T.Chinstrap] 32.4260 67.512 0.480 0.631 -100.369 165.221
C(species)[T.Gentoo] 1375.3540 56.148 24.495 0.000 1264.912 1485.796
==============================================================================
Omnibus: 7.340 Durbin-Watson: 3.036
Prob(Omnibus): 0.025 Jarque-Bera (JB): 5.331
Skew: 0.182 Prob(JB): 0.0696
Kurtosis: 2.508 Cond. No. 3.45
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
ANOVA-Tabelle:
sum_sq df F PR(>F)
C(species) 1.468642e+08 2.0 343.626275 2.892368e-82
Residual 7.244348e+07 339.0 NaN NaNResiduendiagnostik für die Normalverteilungsannahme
Die Normalverteilungsannahme besagt, dass die Residuen (die Unterschiede zwischen beobachteten und vorhergesagten Werten) normalverteilt sein sollten. Diese Annahme ist wichtig für inferenzstatistische Zwecke wie Hypothesentests und Konfidenzintervalle.
Was genau sollte normalverteilt sein?
Es ist wichtig zu betonen, dass nicht unbedingt die Daten selbst normalverteilt sein müssen, sondern die Residuen des Modells. Dies ist ein häufiges Missverständnis. Wir interessieren uns also nicht unbedingt dafür, ob z.B. die Körpergewichte normalverteilt sind, sondern ob die Abweichungen unseres Modells von den tatsächlichen Werten normalverteilt sind.
Option 1: Verteilung der Residuen als Histogramm
Eine einfache Methode, um die Normalverteilungsannahme zu überprüfen, ist das Zeichnen eines Histogramms der Residuen und der Vergleich mit einer Normalverteilungskurve. Die Normalverteilungskurve benötigt ja wie gesagt zwei Parameter: den Mittelwert und die Standardabweichung. Diese können wir aber auch direkt aus den Residuen berechnen, sodass wir die entsprechende Normalverteilungskurve einfach über das Histogramm legen können.
# Residuen für beide Modelle berechnen
lm_residuals = lm_model.resid
anova_residuals = anova_model.resid
# Histogramme mit Normalverteilungskurve
fig, axes = plt.subplots(1, 2, figsize=(15, 6), layout='tight')
# Histogramm für das lineare Regressionsmodell
axes[0].hist(lm_residuals, bins=20, density=True, alpha=0.7, color='skyblue')
x = np.linspace(lm_residuals.min(), lm_residuals.max(), 100)
axes[0].plot(x, stats.norm.pdf(x, lm_residuals.mean(), lm_residuals.std()), 'r-', lw=2)
axes[0].set_title('Histogramm der Residuen: Lineare Regression')
axes[0].set_xlabel('Residuen')
axes[0].set_ylabel('Dichte')
# Histogramm für das ANOVA-Modell
axes[1].hist(anova_residuals, bins=20, density=True, alpha=0.7, color='skyblue')
x = np.linspace(anova_residuals.min(), anova_residuals.max(), 100)
axes[1].plot(x, stats.norm.pdf(x, anova_residuals.mean(), anova_residuals.std()), 'r-', lw=2)
axes[1].set_title('Histogramm der Residuen: ANOVA')
axes[1].set_xlabel('Residuen')
axes[1].set_ylabel('Dichte')
plt.show()
Natürlich passt die Normalverteilungskurve nicht perfekt zu den Residuen - gerade wenn man nicht allzu viele Datenpunkte hat. Dennoch lässt sich so überprüfen, ob die Residuen eine Normalverteilung aufweisen. Wenn die Residuen stark von der Normalverteilung abweichen, könnte dies darauf hindeuten, dass das Modell nicht gut zu den Daten passt oder dass die Annahme der Normalverteilung verletzt ist. Hier sehen beide Histogramme ganz gut aus.
Option 2: Q-Q-Plots
Während Histogramme einen ersten Eindruck vermitteln, sind Q-Q-Plots (Quantil-Quantil-Plots) ein präziseres Werkzeug zur Überprüfung der Normalverteilungsannahme. Auch sie vergleichen die empirische Verteilung der Residuen mit einer theoretischen Normalverteilung.
Ein Q-Q-Plot funktioniert, indem er die empirischen Quantile der Residuen den theoretischen Quantilen einer Normalverteilung gegenüberstellt. Die Quantile teilen eine Verteilung in gleich große Abschnitte ein – zum Beispiel ist das untere Quartil der Wert, unter dem 25 % der Daten liegen. Für den Q-Q-Plot wird berechnet, an welcher Stelle in der Normalverteilung ein bestimmter Datenpunkt erwartet würde, wenn die Daten wirklich normalverteilt wären. Dann wird dieser theoretische Wert mit dem tatsächlich beobachteten Wert verglichen.
Wenn die Residuen normalverteilt sind, sollten die Punkte im Q-Q-Plot nahe an einer Geraden liegen. Abweichungen von dieser Geraden weisen auf Abweichungen von der Normalverteilung hin.
fig, axes = plt.subplots(1, 2, figsize=(15, 6), layout='tight')
# Q-Q-Plot für das lineare Regressionsmodell
sm.qqplot(lm_residuals, line='s', ax=axes[0])
axes[0].set_title('Q-Q-Plot: Lineare Regression (Flossenlänge ~ Körpergewicht)')
# Q-Q-Plot für das ANOVA-Modell
sm.qqplot(anova_residuals, line='s', ax=axes[1])
axes[1].set_title('Q-Q-Plot: ANOVA (Körpergewicht ~ Pinguinart)')
plt.show()
Interpretation:
- Ein guter Q-Q-Plot sollte zeigen, dass die Punkte nahe der 45-Grad-Linie liegen.
- Abweichungen an den Enden (Tails) des Plots weisen auf “schwere Enden” (heavy tails) hin, was bedeutet, dass extreme Werte in den Daten häufiger auftreten als in einer Normalverteilung erwartet.
- S-förmige Muster können auf Schiefe hindeuten.
Bei unseren Modellen sehen beide Q-Q-Plots gut aus.
Um besser beurteilen zu können, ob die Punkte im Q-Q-Plot tatsächlich auf einer Linie liegen (was auf Normalverteilung hindeuten würde), kann man mit dem Argument line eine Referenzlinie hinzufügen. Wir verwenden hier line='s', da diese Option eine Linie erzeugt, die speziell an die nicht-standardisierten Residuen angepasst ist - sie verläuft durch das erste und dritte Quartil der Daten. Weitere Optionen sind:
-
line='r': Erzeugt eine robuste Regressionslinie, die weniger empfindlich auf Ausreißer reagiert -
line='45': Zeichnet eine 45°-Diagonale, die nur sinnvoll ist, wenn die Daten/Residuen bereits standardisiert sind
Standardisierte Residuen erhält man, indem man jeden Residualwert durch (Wert - Mittelwert)/Standardabweichung umrechnet, was zu einer Verteilung mit Mittelwert 0 und Standardabweichung 1 führt. Diese Standardisierung kann nützlich sein, weil Werte außerhalb des Bereichs ±2 direkt als statistisch auffällig interpretiert werden können. In diesem Workshop bleiben wir jedoch bei den ursprünglichen Residuen, um die tatsächliche Größenordnung der Abweichungen besser sichtbar zu machen.
Option 3: Statistische Tests für Normalverteilung
Neben visuellen Methoden können wir auch formale statistische Tests durchführen, um die Normalverteilungsannahme zu überprüfen. Der wohl gängigste Test ist der Shapiro-Wilk-Test. Eine weitere Möglichkeit ist der Jarque-Bera-Test. Beide Tests haben als Nullhypothese, dass die Daten normalverteilt sind. Demnach würde ein p-Wert < 0.05 bedeuten, dass die Nullhypothese abgelehnt wird und die Daten wahrscheinlich nicht normalverteilt sind.
# Shapiro-Wilk-Test
print('Shapiro-Wilk-Test p-Werte:')
print(f'Lineare Regression: p = {stats.shapiro(lm_residuals).pvalue:.3f}')
print(f'ANOVA: p = {stats.shapiro(anova_residuals).pvalue:.3f}')
# Jarque-Bera-Test
print('\nJarque-Bera-Test p-Werte:')
print(f'Lineare Regression: p = {jarque_bera(lm_residuals)[1]:.3f}')
print(f'ANOVA: p = {jarque_bera(anova_residuals)[1]:.3f}')Shapiro-Wilk-Test p-Werte:
Lineare Regression: p = 0.112
ANOVA: p = 0.051
Jarque-Bera-Test p-Werte:
Lineare Regression: p = 0.061
ANOVA: p = 0.070Interpretation:
- Keiner der Tests hat einen p-Wert < 0.05, sodass wir die Nullhypothese nicht ablehnen können. Das bedeutet, dass die Residuen der Modelle als normalverteilt betrachtet werden können.
Es sei darauf hingewiesen, dass die Verwendug eines Tests zur Prüfung von einer Modellannahme natürlich komfortabel wirkt, da uns die Entscheidung ob die Annahme verletzt ist oder nicht, abgenommen wird. Anstatt einen Q-Q-Plot anzuschauen, der weder perfekt, noch schrecklich aussieht, könnten wir einfach einen Test durchführen und uns auf das Ergebnis verlassen. Ein Test mit seiner Grenze bei 0.05 gibt uns schließlich immer eine klare Ja-Nein-Entscheidung.
Genau das ist allerdings auch das Problem: Die Realität ist nicht immer so schwarz-weiß. Ein p-Wert von 0.051 ist nicht unbedingt gleichbedeutend mit “nicht normalverteilt”, während ein p-Wert von 0.049 “normalverteilt” bedeutet. Tatsächlich ist der p-Wert ja nur eine Wahrscheinlichkeit, die angibt, wie wahrscheinlich es ist, dass wir die beobachteten Daten erhalten würden, wenn die Nullhypothese wahr wäre.
Darüber hinaus sind solche Tests nicht immer zuverlässig, insbesondere bei kleinen Stichproben. Sie können auch empfindlich auf Ausreißer reagieren und in solchen Fällen falsche Ergebnisse liefern. Daher sollten sie immer in Verbindung mit visuellen Methoden interpretiert werden.
Eine zitierbare Diskussion zu diesem Thema findet sich in der Publikation What’s normal anyway? Residual plots are more telling than significance tests when checking ANOVA assumptions (Kozak & Piepho, 2017; Diese Quelle kann, aber muss nicht gelesen werden!)
Tendeziell sind also die visuellen Prüfungen mit den Residuenplots die erste Wahl, während die Tests eher als zusätzliche Information dienen sollten. Das gilt nicht nur für die Normalverteilungsannahme.
Residuendiagnostik für die Varianzhomogenitätsannahme
Die Annahme der Varianzhomogenität (auch Homoskedastizität genannt) besagt, dass die Varianz der Residuen für alle Werte der Prädiktoren konstant sein sollte. Wenn diese Annahme verletzt wird, spricht man von Varianzheterogenität oder Heteroskedastizität.
Residuen-vs-Fitted-Plots
Der grundlegende Plot zur Überprüfung der Varianzhomogenität ist der Residuen-vs-Fitted-Plot, der die Residuen gegen die vorhergesagten (Fitted) Werte aufträgt:
fig, axes = plt.subplots(1, 2, figsize=(15, 6), layout='tight')
# Residuen-vs-Fitted-Plot für das lineare Regressionsmodell
axes[0].scatter(lm_model.fittedvalues, lm_model.resid, alpha=0.7)
axes[0].axhline(y=0, color='r', linestyle='-')
axes[0].set_title('Residuen vs. Fitted: Lineare Regression')
axes[0].set_xlabel('Vorhergesagte Werte')
axes[0].set_ylabel('Residuen')
# Residuen-vs-Fitted-Plot für das ANOVA-Modell
axes[1].scatter(anova_model.fittedvalues, anova_model.resid, alpha=0.7)
axes[1].axhline(y=0, color='r', linestyle='-')
axes[1].set_title('Residuen vs. Fitted: ANOVA')
axes[1].set_xlabel('Vorhergesagte Werte')
axes[1].set_ylabel('Residuen')
plt.show()
Interpretation:
- In einem idealen Fall sollten die Residuen zufällig um die Nulllinie (rote Linie) verteilt sein, ohne erkennbares Muster.
- Die Streuung der Residuen sollte über den gesamten Bereich der vorhergesagten Werte etwa gleich sein.
- Beide Plots sehen gut aus - wir können von Varianzhomogenität ausgehen.
Standardisierte Residuen vs. Fitted Plot
Eine leistungsstärkere Variante des Residuen-vs-Fitted-Plots verwendet standardisierte Residuen anstelle der Rohresiduen. Diese Abwandlung bietet zwei Vorteile:
Einheitliche Skala: Standardisierte Residuen sind in Einheiten der Standardabweichung ausgedrückt, was die Interpretation vereinfacht und einen konsistenten Maßstab bietet - also auch über verschiedene Modelle und Datensätze hinweg.
Statistische Beurteilung: Werte außerhalb des Bereichs von ±2 oder ±3 Standardabweichungen könnten als statistische Ausreißer identifiziert werden, da wir wissen, dass bei normalverteilten Daten etwa 95% der Werte innerhalb von ±2 Standardabweichungen liegen sollten.
fig, axes = plt.subplots(1, 2, figsize=(15, 6), layout='tight')
# Standardisierte Residuen vs. Fitted für das lineare Regressionsmodell
axes[0].scatter(lm_model.fittedvalues, lm_model.get_influence().resid_studentized_internal, alpha=0.7)
axes[0].axhline(y=0, color='r', linestyle='-')
axes[0].axhline(y=2, color='g', linestyle='--')
axes[0].axhline(y=-2, color='g', linestyle='--')
axes[0].set_title('Standardisierte Residuen vs. Fitted: Lineare Regression')
axes[0].set_xlabel('Vorhergesagte Werte')
axes[0].set_ylabel('Standardisierte Residuen')
# Standardisierte Residuen vs. Fitted für das ANOVA-Modell
axes[1].scatter(anova_model.fittedvalues, anova_model.get_influence().resid_studentized_internal, alpha=0.7)
axes[1].axhline(y=0, color='r', linestyle='-')
axes[1].axhline(y=2, color='g', linestyle='--')
axes[1].axhline(y=-2, color='g', linestyle='--')
axes[1].set_title('Standardisierte Residuen vs. Fitted: ANOVA')
axes[1].set_xlabel('Vorhergesagte Werte')
axes[1].set_ylabel('Standardisierte Residuen')
plt.show()
Interpretation:
- Die grünen gestrichelten Linien bei +2 und -2 markieren den Bereich, in dem etwa 95% der standardisierten Residuen liegen sollten, wenn sie normalverteilt sind.
- Punkte außerhalb dieses Bereichs sind potenzielle Ausreißer, die genauer untersucht werden könnten.
- Ein Trichterförmiges Muster (zunehmende Streuung bei höheren vorhergesagten Werten, also von links nach rechts) würde auf Heteroskedastizität hindeuten, was hier nicht der Fall ist.
Scale-Location Plot
Der Scale-Location Plot (auch Spread-Location Plot genannt) ist eine weitere nützliche Variation des Residuenplots, der speziell für die Diagnose von Varianzheterogenität entwickelt wurde. Im Gegensatz zum standardisierten Residuenplot, der sowohl positive als auch negative Werte zeigt, fokussiert sich dieser Plot ausschließlich auf die Größe (Magnitude) der Abweichungen.
Die Besonderheit: Er trägt die Wurzel der absoluten standardisierten Residuen gegen die vorhergesagten Werte auf. Die Wurzeltransformation wird angewendet, um die Verteilung der Residuengrößen zu stabilisieren und Muster besser erkennbar zu machen. Dies macht den Plot besonders empfindlich für Veränderungen in der Streuung der Residuen über den Bereich der vorhergesagten Werte.
fig, axes = plt.subplots(1, 2, figsize=(15, 6), layout='tight')
# Scale-Location Plot für das lineare Regressionsmodell
std_resid = lm_model.get_influence().resid_studentized_internal
sqrt_abs_std_resid = np.sqrt(np.abs(std_resid))
axes[0].scatter(lm_model.fittedvalues, sqrt_abs_std_resid, alpha=0.7)
axes[0].set_title('Scale-Location Plot: Lineare Regression')
axes[0].set_xlabel('Vorhergesagte Werte')
axes[0].set_ylabel('√|Standardisierte Residuen|')
# Scale-Location Plot für das ANOVA-Modell
std_resid = anova_model.get_influence().resid_studentized_internal
sqrt_abs_std_resid = np.sqrt(np.abs(std_resid))
axes[1].scatter(anova_model.fittedvalues, sqrt_abs_std_resid, alpha=0.7)
axes[1].set_title('Scale-Location Plot: ANOVA')
axes[1].set_xlabel('Vorhergesagte Werte')
axes[1].set_ylabel('√|Standardisierte Residuen|')
plt.show()
Interpretation:
- In einem idealen Fall sollten die Punkte zufällig um eine horizontale Linie verteilt sein, ohne erkennbares Trend- oder Muster.
- Dieser Plot ist besonders gut darin, systematische Änderungen in der Residuenvarianz zu erkennen - beispielsweise einen ansteigenden oder abfallenden Trend, der auf Heteroskedastizität hindeuten würde.
- Bei beiden unserer Modelle sehen wir keinerlei Muster, die auf Heteroskedastizität hindeuten würden.
Statistische Tests für Varianzhomogenität
Neben visuellen Methoden gibt es auch statistische Tests zur Überprüfung der Varianzhomogenität. Allerdings soll hier nochmal betont werden, dass visuelle Diagnosen in der Regel aussagekräftiger und robuster sind als formale Tests, da sie Muster und Zusammenhänge aufzeigen können, die in p-Werten nicht erfasst werden. Dennoch können Tests in bestimmten Situationen hilfreich sein, um Entscheidungen zu objektivieren. Hier sind drei der gängigsten Tests:
-
Breusch-Pagan-Test (
statsmodels.stats.diagnostic.het_breuschpagan):- Testet, ob die Varianz der Residuen mit den Prädiktoren zusammenhängt
- Besonders geeignet für lineare Regressionsmodelle - nicht für ANOVA-Modelle
- Die Nullhypothese ist Homoskedastizität (konstante Varianz)
-
Levene-Test (
scipy.stats.levene):- Vergleicht die Varianz zwischen verschiedenen Gruppen
- Robuster gegenüber Abweichungen von der Normalverteilung als andere Tests
- Besonders geeignet für Gruppenvergleiche (ANOVA-Modelle)
-
Brown-Forsythe-Test (
scipy.stats.levene(center='median')):- Eine Variante des Levene-Tests, die den Median statt des Mittelwerts verwendet
- Noch robuster bei nicht-normalverteilten Daten
- Wird in Python über den Levene-Test mit dem Parameter
center='median'aufgerufen
Dabei ist anzumerken, dass der Breusch-Pagan-Test für ANOVA-Modelle oft weniger geeignet ist. In klassischen ANOVA-Modellen mit kategorialen Prädiktoren (z.B. Gruppenvergleichen) ist die Varianz innerhalb jeder Gruppe separat zu betrachten. Der BP-Test testet aber die Beziehung zwischen Residuen und Prädiktoren linear und global, was nicht ganz zur Gruppenstruktur passt. Für ANOVA-Modelle sind daher Levene- oder Brown-Forsythe-Test meistens die bessere Wahl.
Umgang mit Verletzungen der Annahmen
Wie wir gesehen haben, werden bei unseren Modellen einige Annahmen verletzt. Was können wir tun, wenn dies der Fall ist?
Datentransformationen
Eine häufige Lösung bei Verletzungen der Normalverteilungs- und Varianzhomogenitätsannahmen ist die Transformation der abhängigen Variable. Gängige Transformationen sind:
- Logarithmische Transformation: log(y)
- Quadratwurzeltransformation: sqrt(y)
- Box-Cox-Transformation: Eine Verallgemeinerung, die den besten Transformationsparameter λ bestimmt
Man könnte die logarithmische Transformation für unser lineares Regressionsmodell also wie folgt ausprobieren:
# Logarithmische Transformation der abhängigen Variable
penguins_clean['log_body_mass'] = np.log(penguins_clean['body_mass_g'])
log_model = smf.ols(formula='log_body_mass ~ flipper_length_mm', data=penguins_clean).fit()Die Transformation der abhängigen Variable kann helfen, die Annahmen des linearen Modells besser zu erfüllen. In vielen Fällen kann eine einfache logarithmische Transformation Probleme mit schiefen Verteilungen oder Varianzheterogenität beheben. Die Quadratwurzeltransformation ist eine etwas mildere Alternative, die bei leichteren Problemen oft ausreicht.
Bei der Interpretation eines transformierten Modells müssen wir allerdings berücksichtigen, dass sich auch die Bedeutung der Koeffizienten ändert. Bei einer logarithmischen Transformation interpretieren wir die Koeffizienten als prozentuale Veränderungen statt als absolute Veränderungen.
Alternative Modelle und Ansätze
Wenn Datentransformationen nicht ausreichen, gibt es weitere Ansätze:
Robuste Standardfehler: Diese korrigieren für Heteroskedastizität ohne die Modellparameter zu ändern.
Generalisierte Lineare Modelle (GLM): Diese erweitern lineare Modelle auf nicht-normalverteilte Zielvariablen und bieten spezielle Varianzstrukturen für verschiedene Verteilungsfamilien.
Nicht-parametrische Methoden: Diese machen weniger strenge Annahmen über die Datenverteilung und können bei starken Verletzungen der Annahmen eine gute Alternative sein.
Quantilregression: Diese Methode modelliert den Median oder andere Quantile statt des Mittelwerts und ist robuster gegenüber Ausreißern und Heteroskedastizität.
Mixed-Effects-Modelle: Bei gruppierten oder hierarchischen Daten können diese Modelle die Varianzstruktur besser abbilden.
Die Wahl der besten Methode hängt von der spezifischen Situation, den Daten und den Zielen der Analyse ab. In vielen Fällen ist es sinnvoll, mehrere Ansätze zu vergleichen und die Robustheit der Ergebnisse zu prüfen.
Schließlich sei noch klargestellt, dass die Prüfungen der Modellannahmen niemals perfekte Ergebnisse bzw. Entscheidungen liefern können. Es ist immer eine Frage des Abwägens und der Interpretation. In der Praxis ist es oft hilfreich, verschiedene Ansätze zu kombinieren und die Ergebnisse kritisch zu hinterfragen.