import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
np.random.seed(1) # damit die Zufallszahlen reproduzierbar sindDer p-Wert & Statistische Signifikanz
Im vorherigen Kapitel haben wir gelernt, wie man Korrelationen zwischen Variablen berechnet und interpretiert. Dabei haben wir auch die Funktion stats.pearsonr() verwendet, die nicht nur den Korrelationskoeffizienten, sondern auch einen sogenannten p-Wert zurückgibt. In diesem Kapitel werden wir untersuchen, was dieser p-Wert bedeutet und warum er in vielen Bereichen der Statistik und Datenanalyse eine so zentrale Rolle spielt.
P-Werte und der Begriff der “statistischen Signifikanz” gehören zu den am häufigsten verwendeten und gleichzeitig am häufigsten missverstandenen Konzepten in der Statistik. In manchen Regionen und Disziplinen - insbesondere in den Lebenswissenschaften, der Medizin und den Sozialwissenschaften - ist die Angabe von p-Werten nahezu obligatorisch bei der Präsentation von Forschungsergebnissen.
Zunächst generieren wir wieder Beispieldaten, ähnlich wie im vorherigen Kapitel:
# Erzeugen korrelierter Daten
n = 100
x = np.random.normal(0, 1, n) # 100 Zufallszahlen aus Normalverteilung
y1 = x + np.random.normal(0, 0.5, n) # Starke positive Korrelation
y2 = x + np.random.normal(0, 2, n) # Schwache positive Korrelation
y4 = np.random.normal(0, 1, n) # Keine Korrelation
# Berechne Korrelation und p-Wert
corr_y1, p_y1 = stats.pearsonr(x, y1)
corr_y2, p_y2 = stats.pearsonr(x, y2)
corr_y4, p_y4 = stats.pearsonr(x, y4)fig, axs = plt.subplots(1, 3, layout="tight")
fig.set_size_inches(12, 4)
# Subplot für starke positive Korrelation
axs[0].scatter(x, y1)
axs[0].set_title('Starke positive Korrelation')
axs[0].text(0.05, 0.95, f"r = {corr_y1:.3f}\np < 0.0001",
transform=axs[0].transAxes, va='top')
# Subplot für schwache positive Korrelation
axs[1].scatter(x, y2)
axs[1].set_title('Schwache positive Korrelation')
axs[1].text(0.05, 0.95, f"r = {corr_y2:.3f}\np = {p_y2:.6f}",
transform=axs[1].transAxes, va='top')
# Subplot für keine Korrelation
axs[2].scatter(x, y4)
axs[2].set_title('Keine Korrelation')
axs[2].text(0.05, 0.95, f"r = {corr_y4:.3f}\np = {p_y4:.3f}",
transform=axs[2].transAxes, va='top')
plt.show()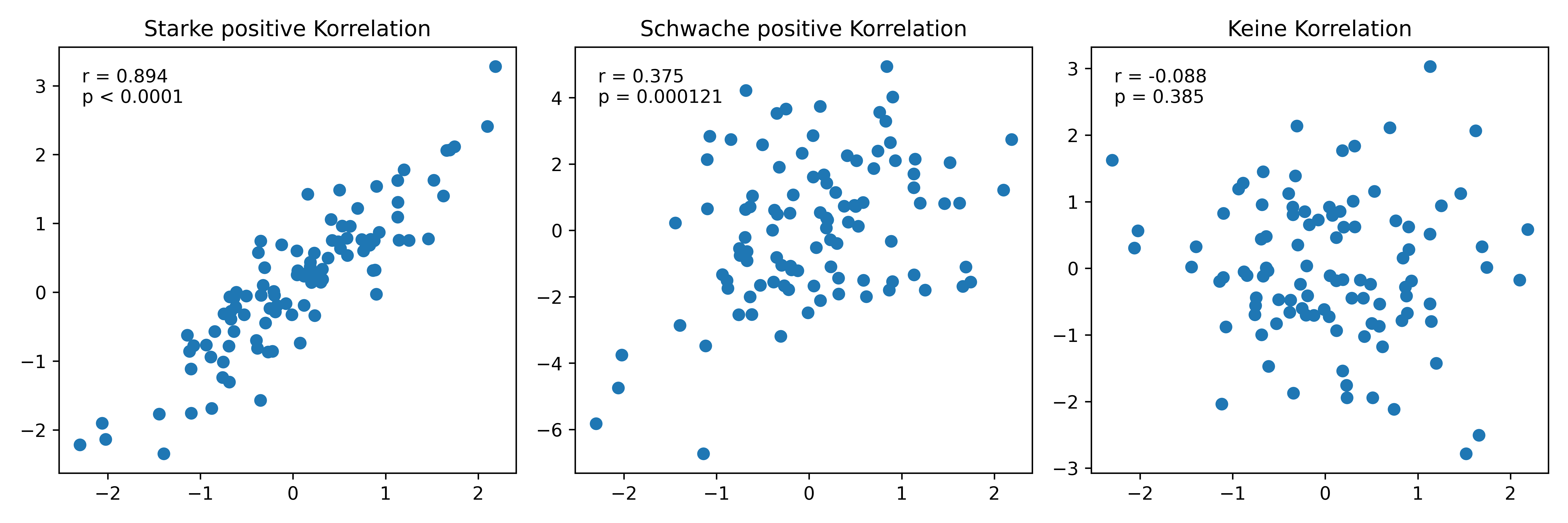
Beim Betrachten des Codes für den obigen Plot können wir mal wieder eine Kleinigkeit lernen: Beim Einfügen des Texts wurde transform=ax.transAxes verwendet. Das sorgt dafür, dass das Koordinatensystem auch pro ax normalisiert ist, also Werte von 0-1 für x- und y-Achse entgegennimmt, anstatt die eigentlichen Werte. Demnach verhält es sich dann also so wie das Koordinatensystem von fig. In diesem Szenario ist das nützlich, da wir so immer an der gleichen Stelle den Text platzieren können, unabhängig von den unterschiedlichen Werten der Achsen pro ax.
print(f"x-y1: r= {corr_y1:.4f}, p={p_y1:.38f}")
print(f"x-y2: r= {corr_y2:.4f}, p={p_y2:.6f}")
print(f"x-y4: r={corr_y4:.4f}, p={p_y4:.3f}")x-y1: r= 0.8943, p=0.00000000000000000000000000000000000539
x-y2: r= 0.3750, p=0.000121
x-y4: r=-0.0879, p=0.385Die Ausgabe zeigt uns, dass die starke Korrelation zwischen x und y1 einen sehr kleinen p-Wert hat, die schwächere Korrelation zwischen x und y2 ebenfalls einen kleinen p-Wert, und die nicht vorhandene Korrelation zwischen x und y4 einen verhältnismäßig großen p-Wert. Aber was bedeutet das eigentlich?
Stichprobe vs. Population: r vs. ρ
Bevor wir den p-Wert genauer betrachten, müssen wir einen wichtigen Unterschied verstehen: den zwischen einer Stichprobe und einer Population.
- Die Population umfasst alle möglichen Beobachtungen, die für unsere Fragestellung relevant sind.
- Eine Stichprobe (Sample) ist eine Teilmenge der Population, die wir tatsächlich beobachten und analysieren können.

Quelle: Everton Gomede
Hier ein paar Beispiele:
| Population | Stichprobe |
|---|---|
| Alle Patienten mit Diabetes in Deutschland | 500 Diabetes-Patienten aus drei Krankenhäusern für eine klinische Studie |
| Alle potenziellen Kunden eines Produkts | 2.000 Konsumenten, die in einer Marktforschungsstudie befragt wurden |
| Alle Eichen in einem Nationalpark | 200 zufällig ausgewählte Eichen zur Untersuchung von Wachstumsmustern |
| Alle registrierten Wähler eines Landes | 1.500 Personen, die für eine Wahlumfrage kontaktiert wurden |
| Alle Verkaufstransaktionen aller Filialen eines Handelsunternehmens | Umsatzdaten von 50 zufällig ausgewählten Filialen aus dem 2. Quartal 2023 |
| Alle vergangenen, aktuellen und zukünftigen Kreditausfälle einer Bank | Kreditausfälle der letzten 5 Jahre, verwendet um zukünftige Ausfallrisiken vorherzusagen |
| Alle Kundenabwanderungsmuster (Churn), die jemals in einem Telekommunikationsunternehmen auftreten werden | Abwanderungsdaten der letzten 24 Monate, verwendet um zukünftiges Kundenverhalten vorherzusagen |
In der Praxis haben wir fast nie Zugriff auf die gesamte Population, sondern nur auf eine Stichprobe. Daraus ergibt sich ein fundamentales Problem: Wir wollen Aussagen über die Population treffen, haben aber nur Informationen aus einer Stichprobe.
Bei der Pearson-Korrelation unterscheiden wir daher zwischen:
- r: Dem Korrelationskoeffizienten der Stichprobe, den wir berechnen können
- ρ (rho): Dem wahren Korrelationskoeffizienten in der Population, den wir nicht kennen
Wir berechnen also immer nur r, obwohl wir eigentlich gern ρ kennen würden. Die grundlegende Frage der Inferenzstatistik lautet nun: Wie können wir von r auf ρ schließen? Genau hier kommen Hypothesentests und p-Werte ins Spiel.
Nullhypothese und p-Werte
Eine der wichtigsten Botschaften, die aus diesem Kapitel mitgenommen werden sollte ist:
Jeder p-Wert ist das Ergebnis eines statistischen Tests, und jeder statistische Test basiert auf einer Nullhypothese (H₀). Die Nullhypothese ist eine Annahme über die Population, die wir zu widerlegen versuchen. Wir haben aber nur eine Stichprobe.
Als Data Scientisten solltet ihr immer, wenn ihr einen p-Wert oder die Worte “statistisch signifikant” rausgebt, auch wissen welchen Test ihr durchgeführt habt und was eigentlich die Nullhypothese war, die getestet wurde.
Es gibt natürlich viele verschiedene Tests und Hypothesen, aber wir werden uns hier wie gesagt auf den Korrelationstest konzentrieren, den wir ja bereits durchgeführt haben. Bei der Pearson-Korrelation lautet die Nullhypothese:
H₀: In der Population besteht keine Korrelation zwischen den Variablen (ρ = 0).
Die Alternativhypothese (H₁) lautet entsprechend:
H₁: In der Population besteht eine Korrelation zwischen den Variablen (ρ ≠ 0).
Generell ist der p-Wert dann so definiert:
Der p-Wert gibt die Wahrscheinlichkeit an, unter der Annahme, dass die Nullhypothese wahr ist, Daten/Ergebnisse zu beobachten, die mindestens so extrem sind wie die in unserer Stichprobe.
Noch weiter vereinfacht:
Bezogen auf unseren Korrelationstest bedeutet das:
Der p-Wert ist die Wahrscheinlichkeit (0-100%), gegeben dass es eigentliche keine Korrelation in der Population gibt (ρ = 0), dass wir aber eine Korrelation (r) beobachten, die mindestens so extrem (verschieden von 0) ist wie die in unserer Stichprobe.
Die “Paralleluniversum”-Analogie
Eine ggf. hilfreiche Analogie in diesem Kontext ist die eines “Paralleluniversums”. Da der p-Wert ja nämlich fest davon ausgeht, dass die Nullhypothese wahr ist, wir ja aber nie wissen ob das wirklich so ist, können wir uns das so vorstellen: Sagen wir es gibt ein Paralleluniversum von dem wir genau wissen, dass H₀ stimmt, also keine Korrelation besteht. In diesem Paralleluniversum könnten wir dann unendlich viele Stichproben ziehen und jedes Mal den Korrelationskoeffizienten berechnen.
Da es definitiv keine Korrelation in der Population gibt (ρ = 0), sollten die Korrelationen in den Stichproben auch 0 sein. Tatsächlich wird es aber immer ein bisschen Abweichungen geben, einfach aufgrund des Zufalls und des Rauschens in den Daten. Somit erhalten wir eigentlich nie ein Ergebnis von exakt 0, also r = 0.00000000000000000000… sondern immer ein bisschen mehr oder weniger. Da wir ja unendlich viele Stichproben nehmen, werden wir bei einigen allein durch Zufall/Pech so untypische Werte in unserer Stichprobe haben, dass das daraus berechnete r sogar ziemlich weit von 0 entfernt ist.
Genau da schließt sich der Bogen zum p-Wert, denn er misst ja genau das: Wie wahrscheinlich ist es, dass wir solche extremen Werte in unserer Stichprobe finden, wenn die Nullhypothese stimmt und es eigentlich keine Korrelation gibt. Je kleiner der p-Wert, desto unwahrscheinlicher ist es, dass unsere Stichprobe aus diesem “Nullhypothesen-Universum” stammt. Ganz unmöglich ist es aber nie.
Beispiel: x-y1
Ausgangslage: p-Wert
Betrachten wir mal die Korrelation zwischen x und y1, die ja stark und positiv ist. Wieder stellen wir uns vor, dass H₀ (in einem Paralleluniversum) eigentlich stimmt. Dann kann man aber eigentlich gar nicht glauben, dass wir überhaupt jemals solche 100 Werte wie hier für y1 mit so einem klaren Trend (siehe nochmals Abbildung oben) finden würden. Ist doch super unwahrscheinlich, oder? Genau, laut p-Wert ist die Wahrscheinlichkeit dafür: 0.000000000000000000000000000000000539 %. Zum Vergleich: Die Chance auf einen Hauptgewinn im Lotto ist 0,00000072 %.
Hier noch ein Versuch das ganze zu visualisieren:
n_pop = 10000
x_pop = np.random.normal(0, 1, n_pop) # zusätzliche 10000 Zufallszahlen
y_pop = np.random.normal(0, 1, n_pop) # zusätzliche 10000 Zufallszahlen
x_pop = np.concatenate([x_pop, x, x]) # Population soll auch genau unsere Stichproben enthalten
y_pop = np.concatenate([y_pop, y1, y4]) # also haben wir letztendlich 10200 Zufallszahlen
fig, axs = plt.subplots(1, 3, layout="tight")
fig.set_size_inches(12, 4)
# Subplot für Population
axs[0].scatter(x_pop, y_pop, color="black")
axs[0].set_title('Population x-y')
# Subplot für x-y1
axs[1].scatter(x_pop, y_pop, color="lightgrey")
axs[1].scatter(x, y1)
axs[1].set_title('Stichprobe x-y1')
# Subplot für x-y4
axs[2].scatter(x_pop, y_pop, color="lightgrey")
axs[2].scatter(x, y4)
axs[2].set_title('Stichprobe x-y4')
plt.show()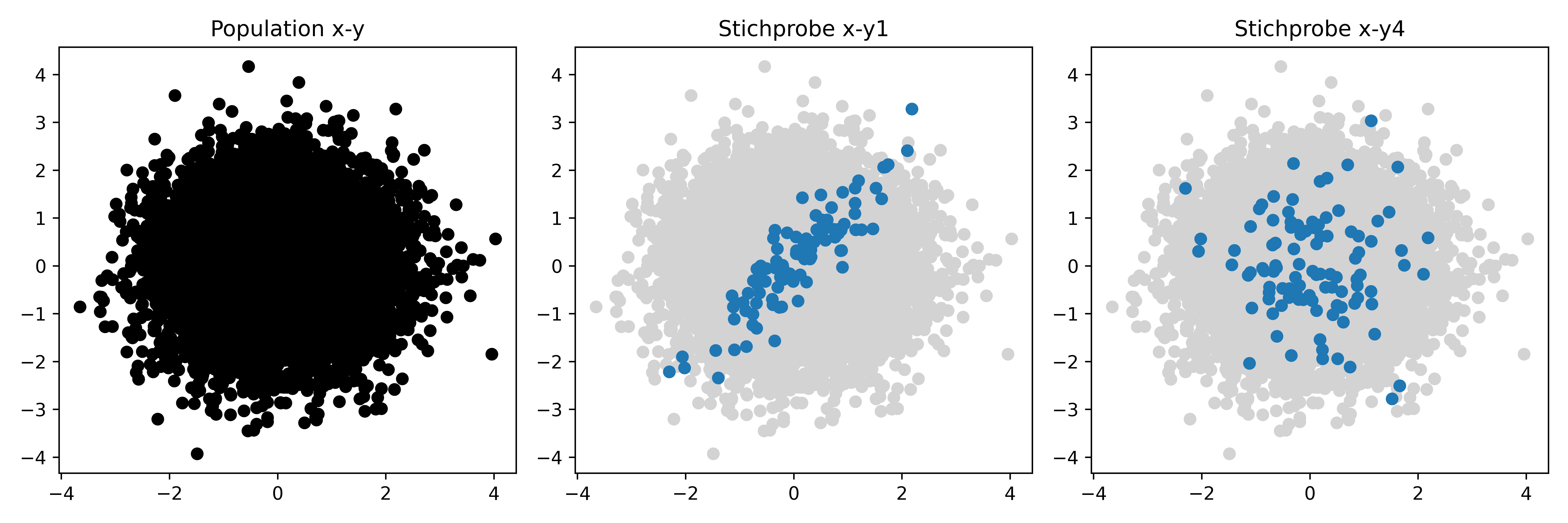
Links soll die Population darstellen werden mit allen Werten, die überhaupt nicht korreliert sind (ρ = 0). Daneben dann unsere jeweilige Stichprobe x-y1 und x-y4. Geht man also davon aus, dass die beiden Stichproben rechts aus dem Topf links gezogen wurden, dann wird schnell klar warum der p-Wert für x-y1 so klein ist und für x-y4 eben deutlich größer.
Schlussfolgerung: H0 verwerfen
Nun, da wir verstanden haben was der p-Wert bedeutet, ergibt es auch Sinn, dass wir bei einem zu kleinen p-Wert (meist <0,05) die Nullhypothese verwerfen - also nicht länger an sie glauben. Sicher haben wir nicht endgültig bewiesen, dass es in der Population wirklich eine Korrelation ≠ 0 gibt, aber wir haben zumindest genug Anhaltspunkte, um die Nullhypothese zu verwerfen. Wir nennen das Ergebnis dann “statistisch signifikant”.
Wenn \(p < 0.05\), dann verwerfen wir die Nullhypothese und akzeptieren die Alternativhypothese.
Wenn \(p \geq 0.05\), dann können wir die Nullhypothese nicht verwerfen.
Wenn ihr all das verstanden habt, könnten wir eigentlich dieses Kapitel beenden, denn genau so funktioniert das mit statistischen Tests und deren p-Werten. Ihr wisst was ein p-Wert ist und kann und ihr versteht was eine Nullhypothese ist und wann man sie verwirft.
Wir wollen uns das ganze aber noch ein wenig auf der Zunge zergehen lassen.
Wichtige Details
H0 verwerfen vs. nicht verwerfen
Ist ein p-Wert zu klein, haben wir genug Anhaltspunkte um die Nullhypothese zu verwerfen. Demnach gehen wir dann eher davon aus, dass die Alternativhypothese stimmt.
Ist ein p-Wert nicht zu klein, haben wir nicht genug Anhaltspunkte um die Nullhypothese zu verwerfen. Demnach gehen wir vorerst weiter davon aus, dass die Nullhypothese stimmt.
Aber Achtung: Wenn ihr die Formulierungen genau lest, seht ihr, dass ein großer p-Wert letztendlich gar nichts beweist. Es zeigt nur, dass wir nicht genug Beweise haben um die Nullhypothese zu verwerfen. Es beweist nicht, dass die Nullhypothese stimmt. Es kann nämlich auch sein, dass wir einfach nicht genug Daten haben um die Nullhypothese zu verwerfen, obwohl sie in Wirklichkeit falsch ist.
Statistische Signifikanze vs. Praktische Relevanz
Ein weiteres Missverständnis ist die Gleichsetzung von “statistisch signifikant” mit “wichtig” oder “relevant”. Im umgangssprachlichen Gebrauch ist das vielleicht so, dass etwas signifikant ist, wenn es wichtig ist oder heraussticht. Der Begriff “statistische Signifikanz” hat aber nur die sehr spezifische Bedeutung, die wir oben besprochen haben: Der p-Wert ist kleiner als ein bestimmte Schwellenwert (meist 0,05). Es beispielsweise gut möglich, dass jemand unser Ergebnis von oben wie folgt wiedergibt:
“Wir haben eine signifikante Korrelation zwischen x und y1 gefunden.”
- Suboptimale Formulierung
Das hört sich für einige vielversprechender an als es ist. Wenn man es ganz genau nimmt und unmissverständlich ausdrücken möchte, so könnte man stattdessen das selbe Ergebnise wie folgt formulieren:
“Unsere Analyse ergab eine schwache bis moderate Korrelation zwischen x und y1 (r = 0,375), die statistisch signifikant ist (p < 0,001).”
- bessere Formulierung
Besser an dieser Formulierung ist:
- Es wird explizit “statistisch signifikant” erwähnt, sodass klar ist, dass es sich nicht um eine subjektive Einschätzung der Stärke oder Relevanz handelt.
- Wir bekommen sowohl die Stärke der Korrelation als auch den p-Wert als Zahl genannt.
- Es wird nicht nur gesagt, dass es eine Korrelation gibt, sondern auch wie stark sie ist.
- Es wird nicht nur gesagt, dass der p-Wert klein ist, sondern auch wie klein er ist.
Tatsächlich kann die genauere Formulierung sogar etwas enttäuschend wirken, da die Korrelation mit 0,375 ja nicht besonders stark ist. Und selbst wenn wir über den Aspekt der statistischen Signifikanz nachdenken, so haben wir ja lediglich die Nullhypothese verworfen, dass es keine Korrelation gibt. Ob die wahre Korrelation nun klein oder groß oder positiv oder negativ ist, wissen wir immer noch nicht genau. Wir wissen nur, dass die wahre Korrelation wahrscheinlich nicht 0 ist und, dass die Korrelation unserer Stichprobe 0,375 ist, sodass die wahre Korrelation wahrscheinlich auch irgendwo in der Nähe von 0,375 liegt.
Das war’s. Ob es in der Praxis relevant ist, dass zwei Merkmale eine Korrelation von 0,375 haben, ist eine ganz andere Frage. Das hängt von der konkreten Anwendung und dem Kontext ab und muss von den Fachepxerten beurteilt werden.
Die Willkür der 0,05-Grenze
Prinzipiell ist der Ansatz mit dem zu kleinen p-Wert nachvollziehbar und gut. Je länger man aber darüber nachdenkt was genau “zu klein” denn bedeutet, desto mehr kann man sich über den meist geltenden Schwellwert von 0,05 streiten. Diese Grenze, oft als α-Niveau oder Signifikanzniveau bezeichnet, wurde vom Statistiker Ronald Fisher in den 1920er Jahren eher willkürlich gewählt und hat sich seitdem als Konvention etabliert.
Es gibt keinen mathematischen oder naturwissenschaftlichen Grund, warum gerade 0,05 der “richtige” Schwellenwert sein sollte. Es bedeutet ja lediglich, dass die Wahrscheinlichkeit weniger als 5% beträgt, dass wir solche Daten finden, wenn die Nullhypothese stimmt. In manchen Bereichen werden auch tatsächlich strengere Schwellenwerte verwendet (z.B. 0,01 oder 0,001), in anderen liberalere.
Wenn man den p-Wert richtig versteht, wird klar, dass er ein Kontinuum darstellt und nicht eine binäre “signifikant/nicht signifikant”-Entscheidung. Ein p-Wert von 0,051 (=5,1 %) ist praktisch nicht anders zu interpretieren als ein p-Wert von 0,049 (=4,9 %) obwohl nur letzterer als “signifikant” gilt.
Da dies allerdings zumindest in der Vergangenheit, aber auch heute noch, nicht immer richtig verstanden wird, ergeben sich Probleme wie Publication Bias und P-Hacking (Details dazu folgen gleich).
Signifikanzniveau α vs. p-Wert
Sowohl das Signifikanzniveau \(\alpha\) als auch der p-Wert sind Wahrscheinlichkeiten, die mit Typ-I-Fehlern zusammenhängen. Trotzdem sind sie nicht dasselbe.
Häufig hört man Aussagen wie “Ein P-Wert von 3% bedeutet, dass die Wahrscheinlichkeit eines Typ-I-Fehlers 3% beträgt” oder “Ein Signifikanzniveau von 3% bedeutet, dass die Wahrscheinlichkeit eines Typ-I-Fehlers 3% beträgt”. Beide Aussagen sind falsch, weil sie eine langfristige Eigenschaft mit einer spezifischen Einzelsituation verwechseln.
Das Signifikanzniveau α und der p-Wert beantworten nämlich zwei völlig verschiedene Fragen. Alpha fragt: “Wie oft werden wir uns langfristig irren, wenn wir dieses Verfahren immer wieder anwenden?” Der p-Wert hingegen fragt: “Wie überraschend sind diese spezifischen Daten, falls die Nullhypothese wahr ist?”
Wenn wir einen p-Wert von 3% erhalten, bedeutet das: “Wenn die Nullhypothese wahr wäre, gäbe es nur eine 3%ige Wahrscheinlichkeit, so extreme Daten (oder noch extremere) zu beobachten.” Das ist eine bedingte Wahrscheinlichkeit der Form P(diese Daten | H₀ ist wahr). Was wir aber gerne wüssten, ist eine ganz andere bedingte Wahrscheinlichkeit: P(wir irren uns | diese Entscheidung). Der P-Wert sagt uns etwas über die Wahrscheinlichkeit unserer Daten unter der Annahme, dass H₀ wahr ist. Aber er kann uns nicht sagen, wie wahrscheinlich es ist, dass wir uns mit unserer Entscheidung irren - also mit genau dieser einen Testentscheidung.
Beim Signifikanzniveau ist es ähnlich. Alpha = 5% bedeutet nicht “In diesem Test beträgt die Wahrscheinlichkeit eines Typ-I-Fehlers 5%”. Vielmehr bedeutet es: “Langfristig, über viele identische Experimente hinweg (bei denen H₀ jeweils wahr ist), werden wir in 5% der Fälle fälschlicherweise ‘signifikant’ sagen.”
So funktioniert das System: Wir legen vor dem Test α fest (z.B. 5%) als unsere “Risikobereitschaft”. Nach dem Test berechnen wir den P-Wert aus den Daten. Wenn P < α, entscheiden wir “signifikant”. Dieses System sorgt dafür, dass wir langfristig nur in 5% der Fälle (bei wahrer H₀) einen Fehler machen - es garantiert uns aber keine Aussage über die Fehlerwahrscheinlichkeit in diesem einen spezifischen Test.
Das ist zugegebenermaßen weniger befriedigend als die intuitive Interpretation “3% Fehlerwahrscheinlichkeit”, aber es ist statistisch korrekt. Die unbefriedigende Wahrheit lautet: Wenn unser P-Wert 3% ist und wir “signifikant” entscheiden, können wir für diesen einen Test nicht berechnen, wie wahrscheinlich es ist, dass wir uns irren. Aber das System garantiert uns, dass wir uns langfristig nur in 5% solcher Fälle irren werden.
Diese Klarstellung zeigt auch, warum statistische Entscheidungen auf vorher festgelegten Standards basieren müssen und warum “P-Hacking” (nachträgliches Anpassen von α) das System zerstört. Statistik gibt uns keine Gewissheit für einzelne Fälle, sondern kontrollierte Unsicherheit über viele Fälle hinweg.
Publication Bias und P-Hacking
Der Publication Bias (Publikationsverzerrung) beschreibt die Tendenz, dass Studien mit signifikanten Ergebnissen (p < 0,05) eher publiziert werden als solche mit nicht-signifikanten Ergebnissen. Dies führt zu einer Überrepräsentation signifikanter Ergebnisse in der wissenschaftlichen Literatur.
Also sprich, wenn 100 Forschungsteams dasselbe Experiment durchführen um zu prüfen ob zwei Variablen korreliert sind, die in Wirklichkeit völlig unabhängig sind, dann werden 5 von ihnen (bei einem α-Niveau von 0,05) ein “statistisch signifikantes” Ergebnis finden, einfach nur weil sie Pech hatten und zufällig eine Stichprobe erwischt haben, die eine Korrelation zeigt. Das ist noch kein Problem. Wenn dann aber nur diese 5 Ergebnisse publiziert werden und die anderen 95 nicht, dann entsteht ein Problem, da die Lesenden dann den Eindruck bekommen, dass es tatsächlich eine Korrelation gibt.
Das ganze geht sogar noch weiter: Wenn erstmal klar ist, dass Ergebnisse mit statistischer Signifikanz tatsächlich häufiger publiziert oder stärker wahrgenommen werden, dann folgt leider automatisch, dass einige so lange an ihren Daten und Tests herumschrauben werden, bis ihr Ergebnis endlich auch statistisch signifikant ist. Dieses P-Hacking bezeichnet Praktiken, bei denen Forscher ihre Analysen bewusst oder unbewusst so manipulieren, dass sie signifikante p-Werte erhalten, z.B. durch:
- Mehrfaches Testen ohne Korrektur
- Selektives Berichten von Ergebnissen
- Nachträgliche Formulierung von Hypothesen (“HARKing” - Hypothesizing After Results are Known)
- Ausschließen von “Ausreißern”
- Sammeln weiterer Daten, bis das Ergebnis signifikant wird
Diese Praktiken erhöhen die Wahrscheinlichkeit falscher positiver Ergebnisse erheblich und haben zur sogenannten “Replikationskrise” in vielen wissenschaftlichen Disziplinen beigetragen.
Alternative Ansätze
Angesichts der Probleme mit p-Werten haben Statistiker alternative oder ergänzende Ansätze vorgeschlagen:
- Konfidenzintervalle: Geben einen Bereich an, in dem der wahre Populationsparameter mit einer bestimmten Wahrscheinlichkeit liegt.
- Effektgrößen: Quantifizieren die Stärke eines Zusammenhangs oder Unterschieds.
- Bayes’sche Statistik: Berechnet die Wahrscheinlichkeit einer Hypothese basierend auf den Daten und dem Vorwissen.
- Vorab-Registrierung von Studien: Verhindert P-Hacking durch die Festlegung von Hypothesen und Analyseplänen vor der Datenerhebung.
Häufige Missverständnisse
Es gibt einige Fehlinterpretationen zu dieser Thematik, die einem besonders häufig begegnen. Aus didaktischer Sicht lässt sich auch diskutieren ob es sinnvoll ist, diese überhaupt zu thematisieren, da sie ja eigentlich falsch sind und hoffentlich nicht doch versehentlich in eurem Kopf hängen bleiben. Aber da sie eben so häufig sind, hier die drei wohl häufigsten in Meme-Form:



Zusammenfassung
In diesem Kapitel haben wir das Konzept des p-Werts und der statistischen Signifikanz kennengelernt - fundamentale Konzepte, die in vielen Bereichen der Statistik und Data Science eine zentrale Rolle spielen.
Wir haben gelernt, dass jeder p-Wert das Ergebnis eines statistischen Tests ist und auf einer Nullhypothese basiert. Bei der Korrelation lautet diese Nullhypothese, dass in der Population keine Korrelation zwischen den Variablen besteht (ρ = 0). Der p-Wert gibt dann die Wahrscheinlichkeit an, unter der Annahme dieser Nullhypothese, einen Korrelationskoeffizienten zu beobachten, der mindestens so extrem ist wie der in unserer Stichprobe berechnete.
Wir haben auch den wichtigen Unterschied zwischen Stichprobe und Population verstanden und warum wir statistische Verfahren benötigen, um von der Stichprobe auf die Population zu schließen. Der p-Wert hilft uns dabei zu beurteilen, ob unsere Stichprobenergebnisse wahrscheinlich auf einen tatsächlichen Effekt in der Population hindeuten oder eher durch Zufall zustande gekommen sein könnten.
Die Konvention, p-Werte unter 0,05 als “statistisch signifikant” zu bezeichnen, haben wir kritisch betrachtet und verstanden, dass diese Grenze durchaus willkürlich ist. Wir wissen nun auch, dass “statistisch signifikant” nicht automatisch “wichtig” oder “relevant” bedeutet. Die Stärke eines Effekts (wie z.B. die Höhe eines Korrelationskoeffizienten) ist für die praktische Relevanz oft wichtiger als die bloße statistische Signifikanz.
Schließlich haben wir problematische Praktiken wie Publication Bias und P-Hacking kennengelernt, die zu verzerrten Ergebnissen in der wissenschaftlichen Literatur führen können, sowie alternative Ansätze wie Konfidenzintervalle und Effektgrößen, die p-Werte sinnvoll ergänzen können.
Die korrekte Interpretation von p-Werten und der umsichtige Umgang mit dem Konzept der statistischen Signifikanz sind wesentliche Fähigkeiten für jeden Data Scientist, da sie die Grundlage für evidenzbasierte Entscheidungen bilden und vor voreiligen Schlussfolgerungen schützen.
In dieser Woche gibt es bewusst weniger Lernstoff, um euch die Möglichkeit zu geben, die Inhalte des vorangegangenen Kurses Data Analytics mit Python nachzuholen oder zu vertiefen.
Übungen
Zu diesem Kapitel gibt es keine Übungsaufgaben. Stattdessen soll einer der folgenden Punkte in Erwägung gezogen werden:
Bei Interesse weiter in das Thema einzutauchen, indem über die in “Weitere Ressourcen” verlinkten Materialien hinausgegangen wird.
Versuche das Szenario aus dem Publication Bias Abschnitt zu simulieren: Erzeuge 100 weitere, zufällige Stichproben mit jeweils
xundyWerte und berechen dementsprechend 100 weitere Korrelationskoeffizienten und p-Werte. Wie viele davon sind kleiner als 0,05?Du kannst die Zeit auch nutzen um Kapitel aus Teil 1 Data Analyst nachzuholen.