import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
np.random.seed(1) # damit die Zufallszahlen reproduzierbar sindKonfidenzintervalle & Verteilungen
Im vorherigen Kapitel haben wir p-Werte und statistische Signifikanz kennengelernt. Eine der genannten Alternativen bzw. Ergänzungen waren Konfidenzintervalle (auch: Vertrauensintervalle, Vertrauensbereiche, confidence intervals, CI). In diesem Kapitel werden wir untersuchen, wie Konfidenzintervalle die Unsicherheit unserer statistischen Schätzungen quantifizieren und uns ein umfassenderes Bild unserer Daten liefern können.
Von Punktschätzungen zu Intervallschätzungen
Greifen wir nochmals das Korrelationsbeispiel aus den vorherigen Kapiteln auf:
# Erzeugen korrelierter Daten
n = 100
x = np.random.normal(0, 1, n)
y1 = x + np.random.normal(0, 0.5, n)
r, p_value = stats.pearsonr(x, y1)
print(f"Korrelationskoeffizient r: {r:.4f}")
print(f"p-Wert: {p_value:.38f}")Korrelationskoeffizient r: 0.8943
p-Wert: 0.00000000000000000000000000000000000539Dieser Korrelationskoeffizient r = 0.89 ist eine Punktschätzung - ein einzelner Wert, der unsere beste Schätzung für den unbekannten Populationsparameter (den wahren Korrelationskoeffizienten ρ) darstellt. Der extrem kleine p-Wert zeigt uns, dass diese Korrelation höchstwahrscheinlich nicht zufällig entstanden ist, sondern auch der wahre Populationsparameter ρ vermutlich von 0 verschieden ist.
Abgesehen von der Tatsache, dass ρ nicht 0 sein dürfte, hätten wir aber gerne eine genauere Schätzung, wie groß ρ tatsächlich ist. Wir möchten wissen wie genau unsere Schätzung ist. Würden wir eine andere Stichprobe ziehen, bekämen wir höchstwahrscheinlich einen etwas anderen Wert für r. Genau hier setzen Konfidenzintervalle an: Sie geben uns eine Intervallschätzung statt nur einen Punkt. So können wir es in berechnen:
ci = stats.pearsonr(x, y1).confidence_interval()
print(f"95%-Konfidenzintervall für r: [{ci[0]:.4f}, {ci[1]:.4f}]")95%-Konfidenzintervall für r: [0.8466, 0.9277]Anstatt also nur zu sagen ‘Die Korrelation ist r = 0.89 und statistisch signifikant verschieden von 0, können wir mit einem Konfidenzintervall präziser informieren: ’Wir schätzen den Korrelationskoeffizienten auf 0.8731 mit einem 95%-Konfidenzintervall von [0.85, 0.93]’.
Definition und Interpretation
Ein Konfidenzintervall ist ein Bereich von Werten, der mit einer bestimmten Wahrscheinlichkeit (dem Konfidenzniveau) den wahren Populationsparameter enthält. Das Konfidenzniveau (typischerweise 95%) gibt den Anteil der Intervalle an, die den wahren Parameter enthalten würden, wenn wir den Prozess der Stichprobenziehung und Intervallberechnung viele Male wiederholen würden. Je mehr man darüber nachdenkt, desto weniger inuitiv erscheint das Konzept. Es ist aber wichtig, die genaue Interpretation zu verstehen:
- Korrekte Interpretation: “Wenn wir viele verschiedene Stichproben nehmen und jeweils ein 95%-Konfidenzintervall berechnen, dann würden etwa 95% dieser Intervalle den wahren Populationsparameter enthalten.”
- Falsche Interpretation: “Es besteht eine 95%-Wahrscheinlichkeit, dass der wahre Parameter in diesem speziellen Intervall liegt.”
Der Unterschied mag subtil erscheinen, ist aber philosophisch wichtig: Der wahre Parameter ist eine feste (wenn auch unbekannte) Größe und hat keine “Wahrscheinlichkeit”, in einem bestimmten Intervall zu liegen. Entweder er liegt darin oder nicht.
So oder so geben Konfidenzintervalle uns aber einen Bereich an, bei dem wir uns relativ sicher sind, dass der wahre Parameter darin liegt. Je schmaler das Intervall, desto präziser ist unsere Schätzung.
Formale Darstellung
Allgemein kann ein Konfidenzintervall in der folgenden Form dargestellt werden:
\[\text{Punktschätzung} \pm \text{Kritischer Wert} \times \text{Standardfehler}\]
Die drei Komponenten sind:
- Punktschätzung: Die beste Schätzung des Parameters aus der Stichprobe (z.B. Korrelationskoeffizient r).
- Kritischer Wert: Ein Wert aus der entsprechenden Wahrscheinlichkeitsverteilung (z.B. z-Wert), der vom gewünschten Konfidenzniveau abhängt.
- Standardfehler: Ein Maß für die Variabilität der Punktschätzung, das typischerweise von der Stichprobengröße abhängt.
Wir sollten also nun noch verstehen was ein kritischer Wert, eine Wahrscheinlichkeitsverteilung und eine Standardfehler sind. Um es uns so einfach wie möglich zu machen, wechseln wir dafür aber das Beispiel: Weg von der Korrelation zweier Variablen x und y1, hin zum Mittelwert einer Variable height.
Normalverteilung
Die Normalverteilung (auch Gauß-Verteilung genannt) ist die bekannteste und wichtigste kontinuierliche Wahrscheinlichkeitsverteilung in der Statistik. Viele natürliche Phänomene, aber auch andere zufällige Prozesse folgen einer Normalverteilung: Messfehler in wissenschaftlichen Experimenten, physiologische Merkmale in Populationen (z.B. Körpergröße, Blutdruckwerte), IQ-Werte, Fertigungstoleranzen in der Produktion, Aktienkursrenditen (in kurzen Zeiträumen), thermisches Rauschen in elektronischen Schaltkreisen.
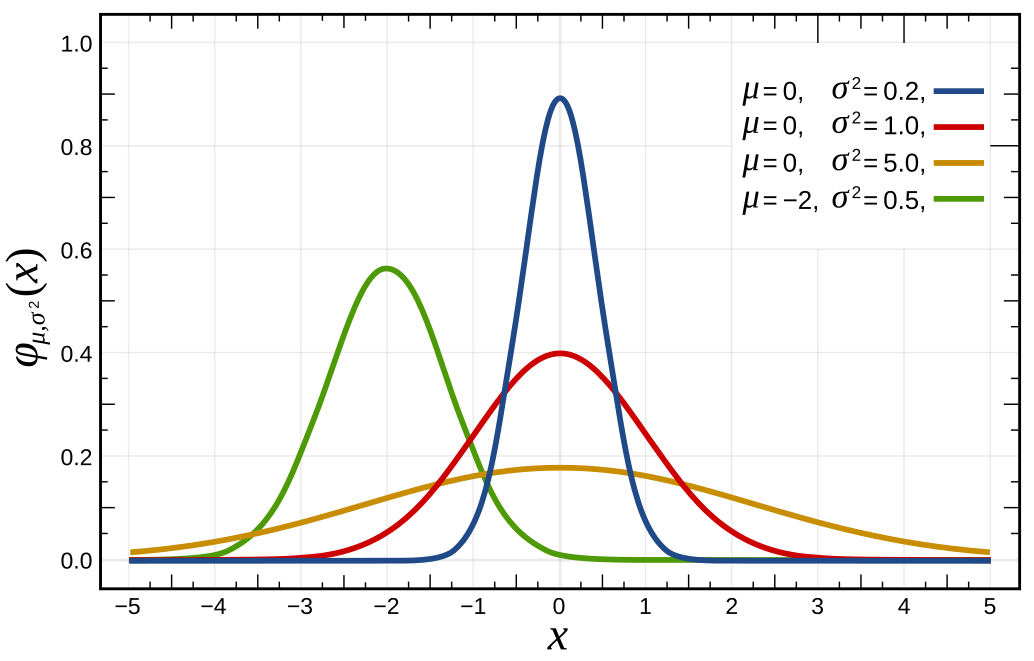
Die Normalverteilung kann mit folgender Formel ausgedrückt werden. Diese sieht zwar kompliziert aus, der Punkt ist aber, dass man nur zwei Parameter braucht, die eingesetzt werden müssen: Den Mittelwert \(\mu\) und die Standardabweichung \(\sigma\).
\[f(x | \mu, \sigma) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{1}{2} \left(\frac{x - \mu}{\sigma}\right)^2}\]
Die Normalverteilung ist symmetrisch um den Mittelwert und hat eine Glockenkurve-Form. Sie hat ihren Höhepunkt bei \(\mu\) und ist je nach Standardabweichung \(\sigma\) unterschiedlich breit.
Quelle: Wikipedia
Standardabweichung wurde erstmals in Kapitel 4.6 Var, StdAbw & Balken behandelt.
Ein klassisches Beispiel für normalverteilte Daten ist die Körpergröße erwachsener Menschen. Natürlich ist nicht jeder Mensch genau gleich groß, aber die Verteilung der Körpergrößen in einer Bevölkerung folgt oft einer Normalverteilung. Einfach ausgedrückt bedeutet das, dass die meisten Menschen durchschnittlich groß sind, während sehr große oder sehr kleine Menschen seltener sind.
Im folgenden Beispiel nehmen wir an, dass es eine Population (z.B. erwachsene Menschen in Deutschland) gibt, deren wahre Verteilung wir kennen: Es sind normalverteilte Werte um den wahren Mittelwert (\(\mu\)) von 174 cm mit einer wahren Standardabweichung (\(\sigma\)) von 10 cm.
Wenn wir aus dieser Population nun Stichproben ziehen, sollten die Werte dieser Stichproben auch Mittelwerte (\(\bar{x}\)) von mehr oder weniger 174 cm haben und mit einer Standardabweichung (\(s\)) von etwa 10 cm schwanken. Und sie sollten eben auch normalverteilt sein. Damit das Histogramm der Stichprobenverteilung einer Normalverteilungskurve ähnelt, müssen wir aber genügend Datenpunkte in der Stichprobe haben. Hier mal ein Beispiel, bei dem wir drei verschiedene Stichproben ziehen - eine kleine (n=10), eine mittlere (n=500) und eine große (n=10000):
Im folgenden Code zur Erzeugung der Histogramme wird eine eigene Funktion plot_histogram definiert, die das Histogramm erstellt und den Stichprobenmittelwert markiert. Diese Funktion wird dann für die drei verschiedenen Stichproben aufgerufen, um die Histogramme zu erstellen. Tatsächlich steht zwischen fig, axes = plt.subplots(...) und plt.show() hier fast nichts außer wie die Funktion definiert und dann drei mal aufgerufen wird. Das ist eine gute Möglichkeit, um Code zu strukturieren und zu vermeiden, dass sich ähnlicher Code wiederholt - vor allem wenn eine Schleife nicht sinnvoll ist bzw. zu umständlich ist.
# Parameter für die Körpergrößen
mean_height = 174 # Mittelwert der Körpergrößen in cm
std_height = 10 # Standardabweichung in cm
# Drei verschiedene Stichprobengrößen
n_small = 10
n_medium = 500
n_large = 10000
# Zufällige Stichproben ziehen
heights_small = np.random.normal(mean_height, std_height, n_small)
heights_medium = np.random.normal(mean_height, std_height, n_medium)
heights_large = np.random.normal(mean_height, std_height, n_large)
# Histogramme mit Normalverteilungskurve erstellen
fig, axes = plt.subplots(1, 3, figsize=(15, 5), layout="tight")
# Funktion zur Erstellung des Histogramms
def plot_histogram(ax, data, n, title_suffix):
# Histogramm
ax.hist(data, bins=30, density=True, alpha=0.6, color='skyblue')
# Mittelwert der Stichprobe markieren
sample_mean = np.mean(data)
ax.axvline(sample_mean, color='black', linestyle='-', alpha=0.8)
# Gleiche Achsengrenzen für alle Plots festlegen
ax.set_xlim(134, 214)
# Formatierung
ax.set_title(f'n = {n} {title_suffix}')
ax.set_xlabel('Körpergröße (cm)')
ax.set_ylabel('Häufigkeitsdichte')
# Beschriftung für den Stichprobenmittelwert
ax.text(sample_mean, 0.03, f'$\\bar{{x}}$ = {sample_mean:.1f}',
ha='center', va='bottom', color='black', backgroundcolor='white')
# Plots für die drei Stichprobengrößen erstellen
plot_histogram(axes[0], heights_small, n_small, "(klein)")
plot_histogram(axes[1], heights_medium, n_medium, "(mittel)")
plot_histogram(axes[2], heights_large, n_large, "(groß)")
plt.suptitle('Körpergrößenverteilung bei unterschiedlichen Stichprobengrößen', fontsize=14)
plt.show()
Diese Abbildung zeigt eindrucksvoll, wie die Stichprobengröße die Genauigkeit unserer Schätzungen beeinflusst:
- Bei einer kleinen Stichprobe (n = 10) weicht der Stichprobenmittelwert oft deutlich vom wahren Populationsmittelwert ab, und die Verteilung sieht wenig nach einer Normalverteilung aus.
- Bei einer mittleren Stichprobe (n = 100) nähert sich die Verteilung bereits besser der Normalverteilungskurve an.
- Bei einer großen Stichprobe (n = 10000) passt die Verteilung fast perfekt zur theoretischen Normalverteilungskurve, und der Stichprobenmittelwert liegt sehr nahe am wahren Populationsmittelwert.
Die 68-95-99,7-Regel
Eine praktische Faustregel für die Normalverteilung ist die 68-95-99,7-Regel (auch bekannt als empirische Regel):
- Etwa 68% der Werte liegen innerhalb einer Standardabweichung vom Mittelwert.
- Etwa 95% der Werte liegen innerhalb von zwei Standardabweichungen vom Mittelwert.
- Etwa 99,7% der Werte liegen innerhalb von drei Standardabweichungen vom Mittelwert.
Diese Regel hilft uns, die Verteilung von Daten intuitiv zu verstehen und einzuschätzen, wie wahrscheinlich bestimmte Abweichungen vom Mittelwert sind.
Nehmen wir uns nochmals die größte Stichprobe und fügen der Verteilung der Körpergrößen diesmal noch entsprechende Informationen visuell hinzu, erhalten wir folgende Abbildung:
sample_mean = np.mean(heights_large)
sample_std = np.std(heights_large)
fig, ax = plt.subplots(figsize=(10, 5), layout="tight")
# Histogramm
ax.hist(heights_large, bins=30, density=True, alpha=0.3, color='skyblue')
# Normalverteilungskurve
x = np.linspace(sample_mean - 4*sample_std, sample_mean + 4*sample_std, 1000)
y = stats.norm.pdf(x, sample_mean, sample_std)
ax.plot(x, y, lw=2, color="blue", alpha=0.5)
# Vertikale Linien für die 68-95-99,7-Regel
ax.axvline(sample_mean, color='black', linestyle='-')
ax.axvline(sample_mean - sample_std, color='purple', linestyle='--', alpha=0.5)
ax.axvline(sample_mean + sample_std, color='purple', linestyle='--', alpha=0.5)
ax.axvline(sample_mean - 2*sample_std, color='red', linestyle='--', alpha=0.5)
ax.axvline(sample_mean + 2*sample_std, color='red', linestyle='--', alpha=0.5)
ax.axvline(sample_mean - 3*sample_std, color='orange', linestyle='--', alpha=0.5)
ax.axvline(sample_mean + 3*sample_std, color='orange', linestyle='--', alpha=0.5)
# Beschriftung für den Stichprobenmittelwert
ax.text(sample_mean, 0.02, f'$\\bar{{x}}$ = {sample_mean:.1f}',
ha='center', va='bottom', color='black', backgroundcolor='white')
ax.set_xlim([134, 214])
ax.set_xlabel('Körpergröße (cm)')
ax.set_ylabel('Häufigkeitsdichte')
plt.show()(134.0, 214.0)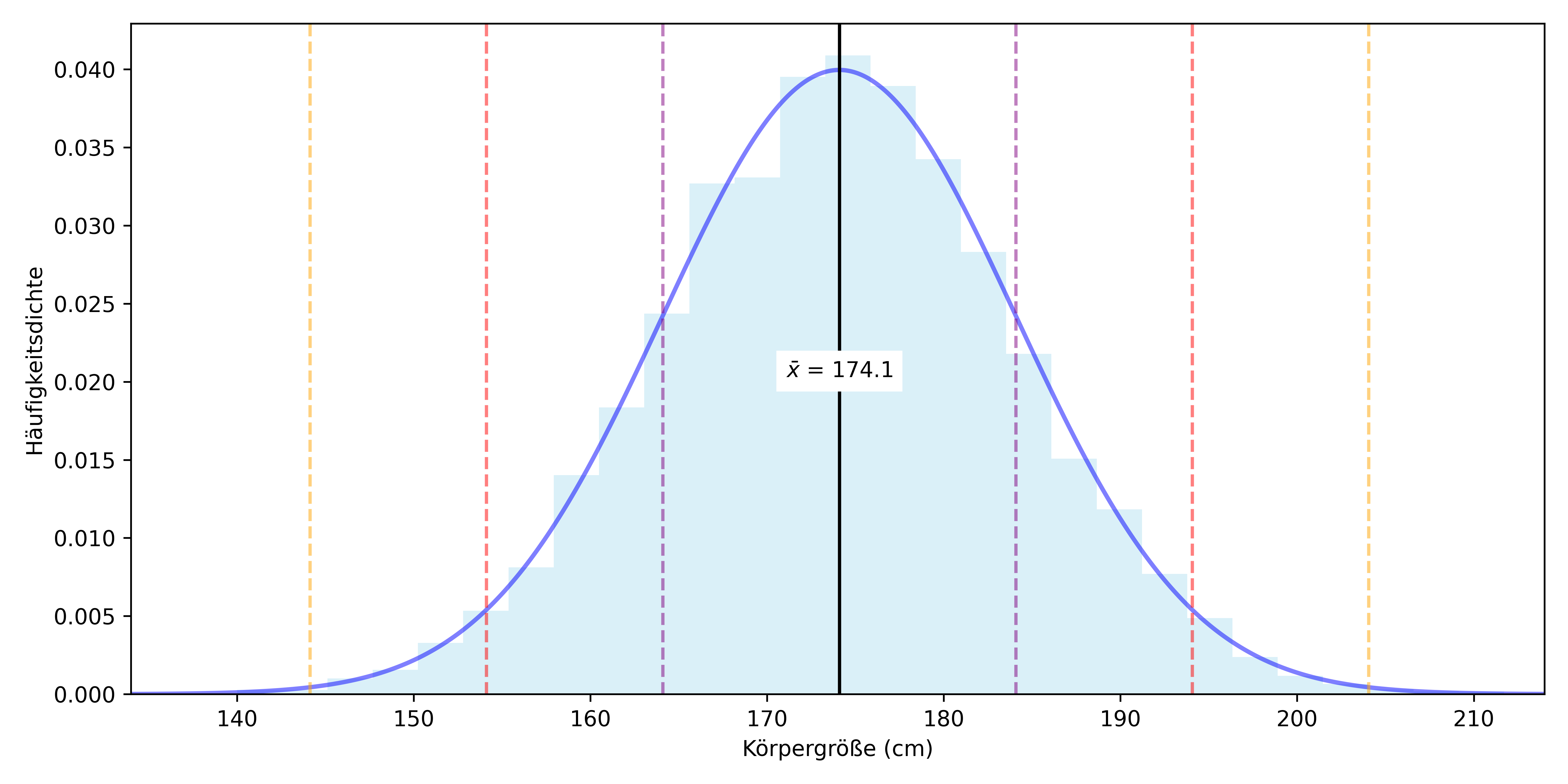
Da die 10.000 Werte annähernd normalverteilt sind, gilt:
- Etwa 68% der Werte liegen zwischen den lilanen Linien.
- Etwa 95% der Werte liegen zwischen den roten Linien.
- Etwa 99,7% der Werte liegen zwischen den orangen Linien.
Wenn wir aber nicht “etwa 95%” sondern z.B. “genau 95%” aller Werte zwischen den roten Linien haben wollen, dann müssten wir nicht 2 Standardabweichungen, sondern vielleicht 1,96 Standardabweichungen nehmen. Das ist der kritische Wert, der bei der Normalverteilung die 95%-Grenze markiert. Bevor wir darauf genauer eingehen, sollten wir aber erstmal noch einen Schritt zurückgehen und lernen was Freiheitsgrade sind.
Freiheitsgrade und kritische Werte
Freiheitsgrade (degrees of freedom, df) bezeichnen in der Statistik die Anzahl der Werte, die frei variieren können, nachdem bestimmte Parameter bereits geschätzt wurden.
Beispiel
Angenommen, wir haben 4 Zahlen mit einem bekannten Mittelwert von 10. Weil der Mittelwert hier schon festgelegt ist, können wir nur 3 der 4 Zahlen frei wählen. Die 4. Zahl wird automatisch bestimmt bzw. ist festgelegt, um den entsprechenden Mittelwert zu erhalten. Wählen wir die ersten drei Zahlen als 8, 9, 11, so muss die vierte Zahl 12 sein, sonst erhalten wir einen anderen Mittelwert. Wählen wir die ersten drei Zahlen als 2, 2, 2, so muss die vierte Zahl 36 sein usw. Der “Grad unserer Freiheheit” ist also 3, weil wir nur 3 Zahlen frei wählen können. Die 4. Zahl ist dann automatisch festgelegt.
Allgemeiner
Allgemein gilt: Wenn wir n Beobachtungen haben und 1 Parameter (wie den Mittelwert) schätzen, haben wir n-1 Freiheitsgrade. Diese Einschränkung entsteht, weil wir eine “Freiheit” verbrauchen, um den Parameter zu schätzen. Der Parameter muss auch nicht unbedingt der Mittelwert sein, sondern kann auch eine andere Größe sein, wie z.B. die Varianz.
Die Verwendung der korrekten Freiheitsgrade ist entscheidend für unverzerrte Schätzungen (unbiased estimates). Beispielsweise bei der Berechnung der Stichprobenvarianz ist die Formel ja \(s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2\). Man sieht also, dass auch hier der Freiheitsgrad \(n-1\), verwendet wird. Es lässt sich mathematisch beweisen, dass wir die Varianz systematisch unterschätzen würden, wenn wir hier stattdessen einfach \(n\) verwenden würden. Das liegt daran, dass wir den Mittelwert bereits geschätzt haben (in Formel \(\bar{x}\)) und damit eine “Freiheit” verloren haben. Die Formel mit n-1 korrigiert diesen Bias. Man spricht hier auch von der Bessel-Korrektur.
Immer mit dem gleichen Prinzip tauchen Freiheitsgrade deshalb oft in statistischen Berechnungen auf, die eine Schätzung eines Parameters erfordern. Beispiele sind die Varianz, die Standardabweichung oder auch die t-Verteilung.
Normalverteilung vs. t-Verteilung
Wie wir bereits gesehen haben, wird in der Statistik häufig davon ausgegangen, dass Daten einer Normalverteilung folgen. Aufgrund dieser Annahme können wir viele statistische Tests durchführen und Konfidenzintervalle schätzen. Allerdings enthält die Formel für die Normalverteilung einen Parameter, der die wahre Standardabweichung \(\sigma\) in der Population beschreibt. Wie so oft kennen wir diesen wahren Wert aber nicht, sondern haben nur die Stichprobenstandardabweichung \(s\) als Schätzer für \(\sigma\). Diese Schätzung führt zu einer zusätzlichen Unsicherheit, die wir berücksichtigen müssen.
Das Problem ist also ähnlich wie bei der Varianzberechnung (siehe oben): Wir müssen für die Unsicherheit korrigieren, die durch das Schätzen von Parametern entsteht. Bei der Varianz korrigieren wir durch die Verwendung von n-1 statt n im Nenner (Bessel-Korrektur). Bei Konfidenzintervallen korrigieren wir, indem wir statt der Normalverteilung die t-Verteilung verwenden:
# Visualisierung der t-Verteilung für verschiedene Freiheitsgrade
fig, ax = plt.subplots(figsize=(10, 6))
x = np.linspace(-4, 4, 1000)
ax.plot(x, stats.norm.pdf(x), 'k-', lw=2, label='Normalverteilung')
# t-Verteilungen für verschiedene Freiheitsgrade
df_values = [1, 3, 8, 30]
colors = ['red', 'orange', 'green', 'blue']
for df, color in zip(df_values, colors):
ax.plot(x, stats.t.pdf(x, df), color=color, label=f't-Verteilung (df={df})')
ax.set_title('Normal- vs. t-Verteilung für verschiedene Freiheitsgrade')
ax.set_xlabel('x')
ax.set_ylabel('Wahrscheinlichkeitsdichte')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
Die t-Verteilung wurde speziell für diesen Zweck entwickelt. Sie:
- Hat dickere “Enden” (heavier tails) als die Normalverteilung
- Berücksichtigt die zusätzliche Unsicherheit bei kleinen Stichproben
- Wird durch Freiheitsgrade charakterisiert, die ihre Form bestimmen
- Nähert sich der Normalverteilung an, wenn die Stichprobengröße wächst
Wenn wir also beispielsweise ein Konfidenzintervall für den Mittelwert von einer Stichprobe (z.B. n=5) berechnen bei der wir davon ausgehen, dass sie normalverteilt sind, nutzen wir in der Praxis gar nicht die exakte Normalverteilung als Basis für unsere Berechnungen, sondern die entsprechende t-Verteilung.
Kritische Werte und wie sie berechnet werden
Kritische Werte sind Schwellenwerte, die eine Wahrscheinlichkeitsverteilung in Bereiche mit bestimmten Wahrscheinlichkeiten unterteilen. Sie definieren sozusagen “Abschneidepunkte”. Die Fläche unter einer Verteilungskurve entspricht 1, da sie die gesamte Wahrscheinlichkeit abdeckt.
Bei einem 95%-Konfidenzintervall (CI) suchen wir den Bereich, der 95% der Fläche abdeckt und zwar nicht irgendwo, sondern um den Mittelwert herum - also in der Mitte. Dementsprechend müssen wir links und rechts Flächen abschneiden, damit nur die mittleren 95% übrig bleiben. Die verbleibenden 5% verteilen sich somit gleichmäßig auf die beiden Enden der Verteilung (2,5% links und 2,5% rechts):
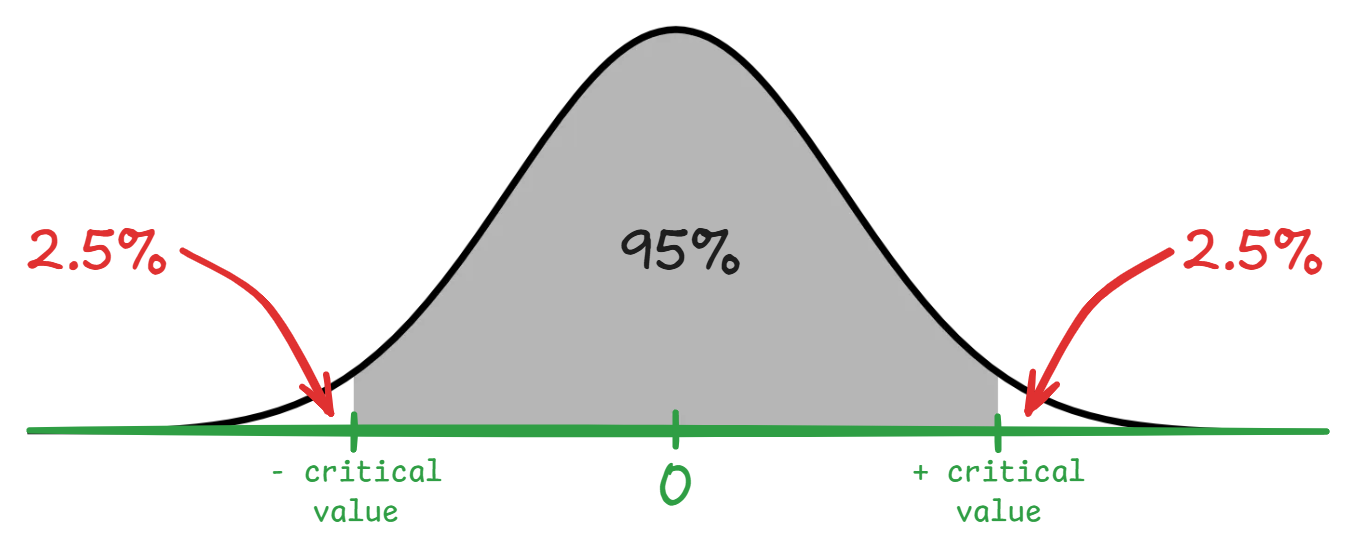
Wenn wir von “genau 95%” aller Werte zwischen den roten Linien sprechen, dann müssen wir nicht 2 Standardabweichungen, sondern etwa 1,96 Standardabweichungen vom Mittelwert aus in beide Richtungen gehen. Dies ist der kritische Wert, der bei der Standardnormalverteilung die 95%-Grenze markiert. Bei der Verwendung der t-Verteilung mit wenigen Freiheitsgraden wäre dieser kritische Wert etwas größer (z.B. 2,201 für df=10 bei 95%-CI), um die zusätzliche Unsicherheit zu berücksichtigen.
Diese kritischen Werte werden bei der Berechnung von Konfidenzintervallen verwendet, wie wir gleich sehen werden.
Standardfehler (vs. Standardabweichung)
Der Standardfehler ist ein Maß für die Genauigkeit einer Schätzung und gibt an, wie weit die Schätzung im Durchschnitt vom wahren Parameter entfernt ist. Er ist eng mit der Standardabweichung verwandt, aber nicht dasselbe:
- Standardabweichung: Maß für die Streuung der Werte in einer Stichprobe.
- Standardfehler: Maß für die Genauigkeit einer Schätzung in einer Stichprobe.
Anders ausgedrückt beschreibt die Standardabweichung die Streuung der Datenpunkte in einer Stichprobe, während der Standardfehler die Streuung der Schätzung selbst - also z.B. des geschätzten Mittelwerts - beschreibt. Man könnte sogar sagen, dass die Standardabweichung beschreibt wie sehr die Datenstreuen, wobei der Standardfehler eines Mittelwerts beschreibt wie sehr die Mittelwerte streuen.
Allerdings berechnen wir ja nur einen Mittelwert, wenn wir eine Stichprobe ziehen. Trotzdem, lässt sich der Standardfehler für diesen Mittelwert berechnen. Für die Körpergrößenbeispiele oben, können wir den Standardfehler des Mittelwerts für die größte Stichprobe berechnen:
Standardabweichung der Werte (\(x\))
\[\sigma_x = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n}}\]
Standardfehler des Mittelwerts der Werte (\(\bar{x}\))
\[\sigma_\bar{x} = \frac{\sigma_x}{\sqrt{n}}\]
Der Standardfehler des Mittelwerts wird also mit zunehmender Stichprobengröße kleiner, und zwar proportional zur Quadratwurzel der Stichprobengröße. Dies bedeutet: Wenn wir die Stichprobengröße vervierfachen, halbiert sich der Standardfehler.
# Standarfehler des MW manuell berechnen (numpy)
se_small = np.std(heights_small, ddof=1) / np.sqrt(n_small)
se_medium = np.std(heights_medium, ddof=1) / np.sqrt(n_medium)
se_large = np.std(heights_large, ddof=1) / np.sqrt(n_large)
# Standardfehler des MW mit sem berechnen (SciPy)
se_small = stats.sem(heights_small)
se_medium = stats.sem(heights_medium)
se_large = stats.sem(heights_large)
print(f"Standardfehler bei n = {n_small}: {se_small:.2f} cm")
print(f"Standardfehler bei n = {n_medium}: {se_medium:.2f} cm")
print(f"Standardfehler bei n = {n_large}: {se_large:.2f} cm")Standardfehler bei n = 10: 4.42 cm
Standardfehler bei n = 500: 0.45 cm
Standardfehler bei n = 10000: 0.10 cmDer Standardfehler ist entscheidend für die Berechnung von Konfidenzintervallen. Für ein 95%-Konfidenzintervall des Mittelwerts berechnen wir:
\[\text{95\% KI} = \bar{x} \pm t_{\text{krit}} \times \sigma_{\bar{x}}\]
Wobei \(t_{\text{krit}}\) der kritische Wert aus der t-Verteilung für ein 95%-Konfidenzintervall und die entsprechenden Freiheitsgrade ist. Bei sehr großem n (>30) nähert sich dieser Wert 1,96 an, dem kritischen Wert der Standardnormalverteilung.
# Eigene Funktion zur Berechnung des Konfidenzintervalls um einen Mittelwert
def calculate_ci(data, confidence=0.95):
n = len(data) # Stichprobengröße
mean = np.mean(data) # Mittelwert
sem = stats.sem(data) # Standardfehler des Mittelwerts
critical_value = stats.t.ppf((1 + confidence) / 2, n - 1) # kritischer t-Wert für df=n-1
return (mean - critical_value*sem, mean + critical_value*sem)
ci_small = calculate_ci(heights_small)
ci_medium = calculate_ci(heights_medium)
ci_large = calculate_ci(heights_large)
print(f"95%-KI bei n = {n_small}: [{ci_small[0]:.1f}, {ci_small[1]:.1f}] cm")
print(f"95%-KI bei n = {n_medium}: [{ci_medium[0]:.1f}, {ci_medium[1]:.1f}] cm")
print(f"95%-KI bei n = {n_large}: [{ci_large[0]:.1f}, {ci_large[1]:.1f}] cm")95%-KI bei n = 10: [161.0, 181.0] cm
95%-KI bei n = 500: [173.4, 175.2] cm
95%-KI bei n = 10000: [173.9, 174.3] cmWie wir sehen, wird das Konfidenzintervall mit zunehmender Stichprobengröße immer schmaler. Bei einer kleinen Stichprobe ist unser Intervall sehr breit, was eine hohe Unsicherheit in unserer Schätzung widerspiegelt. Bei der großen Stichprobe können wir den Populationsmittelwert mit hoher Präzision eingrenzen.
Visualisieren wir die Konfidenzintervalle neben den Mittelwerten:
fig, ax = plt.subplots(figsize=(10, 5), layout="tight")
stichproben = ['n=10', 'n=500', 'n=10000']
means = [np.mean(heights_small), np.mean(heights_medium), np.mean(heights_large)]
cis = [ci_small, ci_medium, ci_large]
# Mittelwerte und Konfidenzintervalle plotten
for i in range(len(stichproben)):
stichprobe = stichproben[i]
mean = means[i]
ci = cis[i]
ax.errorbar(i, mean, yerr=[[mean - ci[0]], [ci[1] - mean]],
fmt='o', capsize=5, capthick=2, color='blue')
ax.set_xticks(range(len(stichproben)))
ax.set_xticklabels(stichproben)
ax.set_ylabel('Körpergröße (cm)')
ax.set_title('Mittelwerte und 95%-Konfidenzintervalle nach Stichprobengröße')
ax.axhline(y=mean_height, color='green', linestyle='-', label='Wahrer Mittelwert')
plt.show()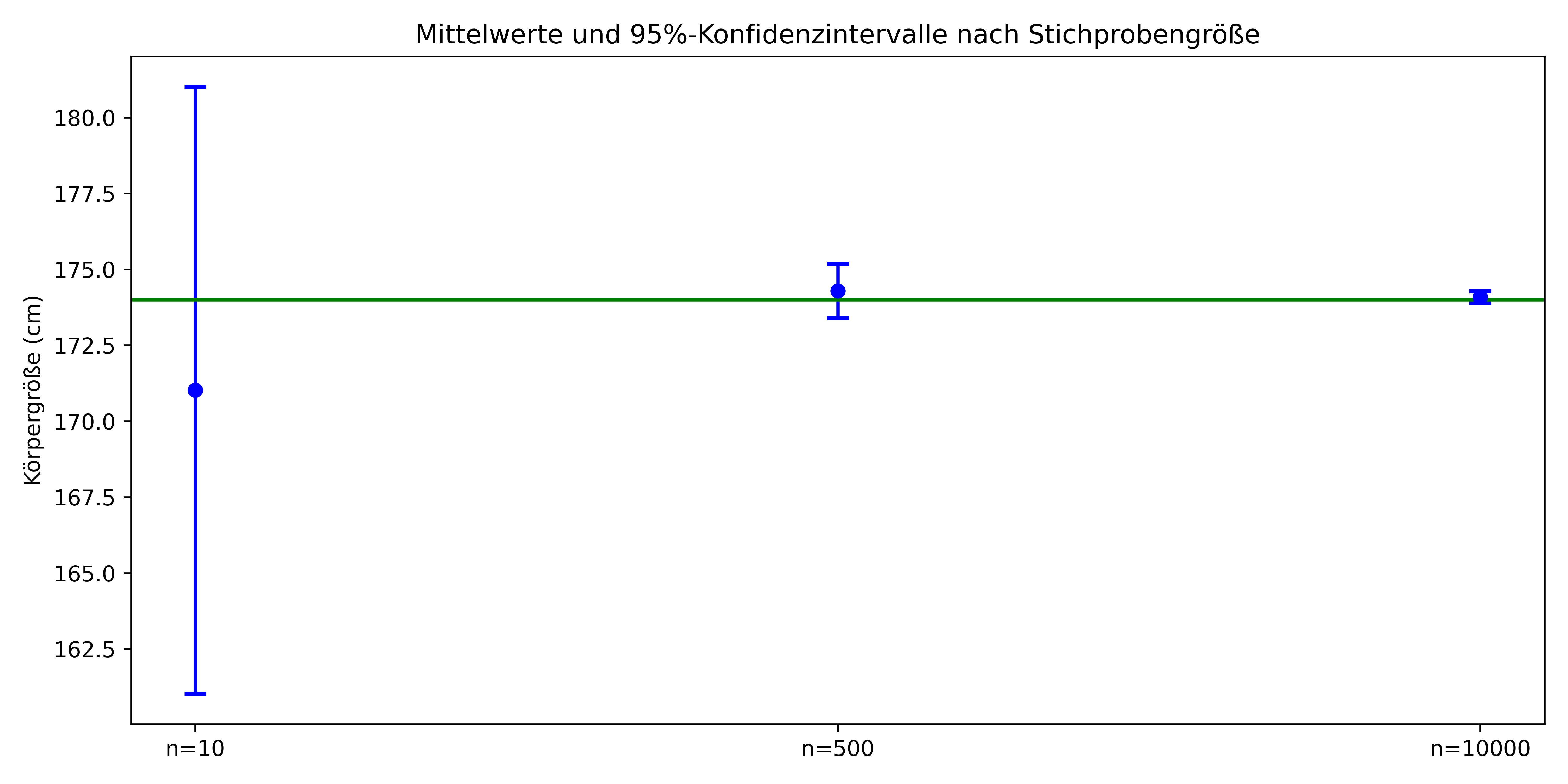
Dieses Diagramm verdeutlicht besonders gut, wie sich die Präzision unserer Schätzung (blau) mit zunehmender Stichprobengröße verbessert und wie das Konfidenzintervall den wahren Populationsparameter (hier den Mittelwert von 174 cm; grün) einschließt oder nicht.
Praktische Anwendung: Vergleich mit p-Werten
Konfidenzintervalle bieten mehrere Vorteile gegenüber reinen p-Werten:
Information über Parametergröße: Während ein p-Wert nur binäre Information liefert (signifikant oder nicht signifikant), zeigt ein Konfidenzintervall auch die geschätzte Größe des Parameters und seinen möglichen Wertebereich. So wissen wir nicht nur, dass ein Effekt existiert, sondern auch wie groß/stark er vermutlich ist.
Präzisionsinformation: Die Breite des Intervalls gibt Aufschluss über die Genauigkeit unserer Schätzung.
Einfachere Interpretation: Konfidenzintervalle können oft intuitiver interpretiert werden, besonders für Nicht-Statistiker.
Andere wichtige Wahrscheinlichkeitsverteilungen
Neben der Normalverteilung gibt es weitere wichtige Wahrscheinlichkeitsverteilungen, die in der Statistik und Data Science häufig verwendet werden. Hier sind einige der wichtigsten:
t-Verteilung
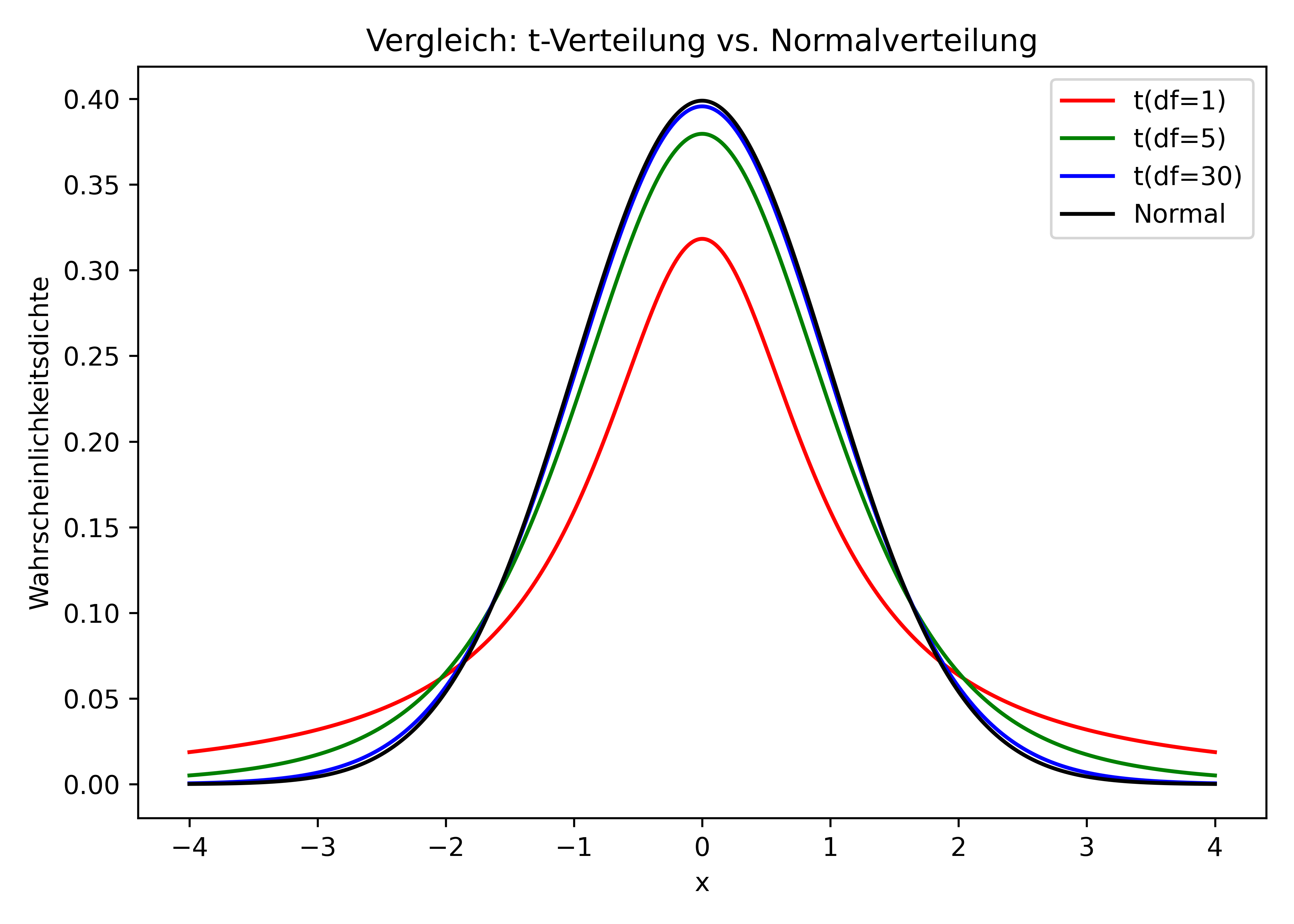
Die t-Verteilung (auch Student’s t-Verteilung genannt) ist der Normalverteilung sehr ähnlich, hat aber “dickere Enden” (engl. heavier tails), was bedeutet, dass extreme Werte wahrscheinlicher sind. Sie wird vor allem für Konfidenzintervalle bei kleinen Stichproben verwendet, wo die wahre Standardabweichung der Population unbekannt ist. Mit zunehmender Stichprobengröße nähert sie sich der Normalverteilung an.
Chi-Quadrat-Verteilung
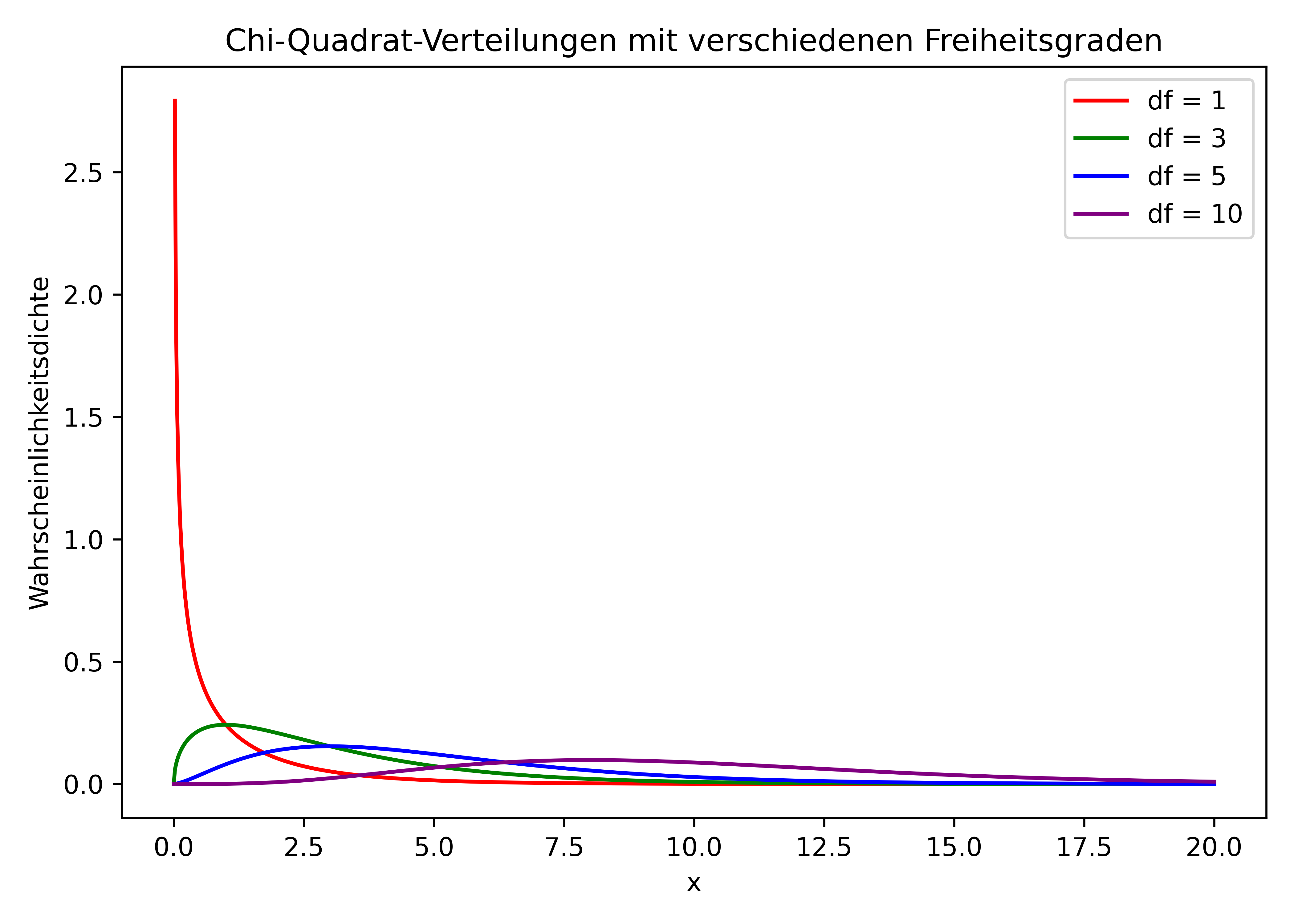
Die Chi-Quadrat-Verteilung (χ²) ist eine rechtsschiefe Verteilung, die häufig bei Hypothesentests bezüglich Varianzen und bei Unabhängigkeitstests verwendet wird.
F-Verteilung
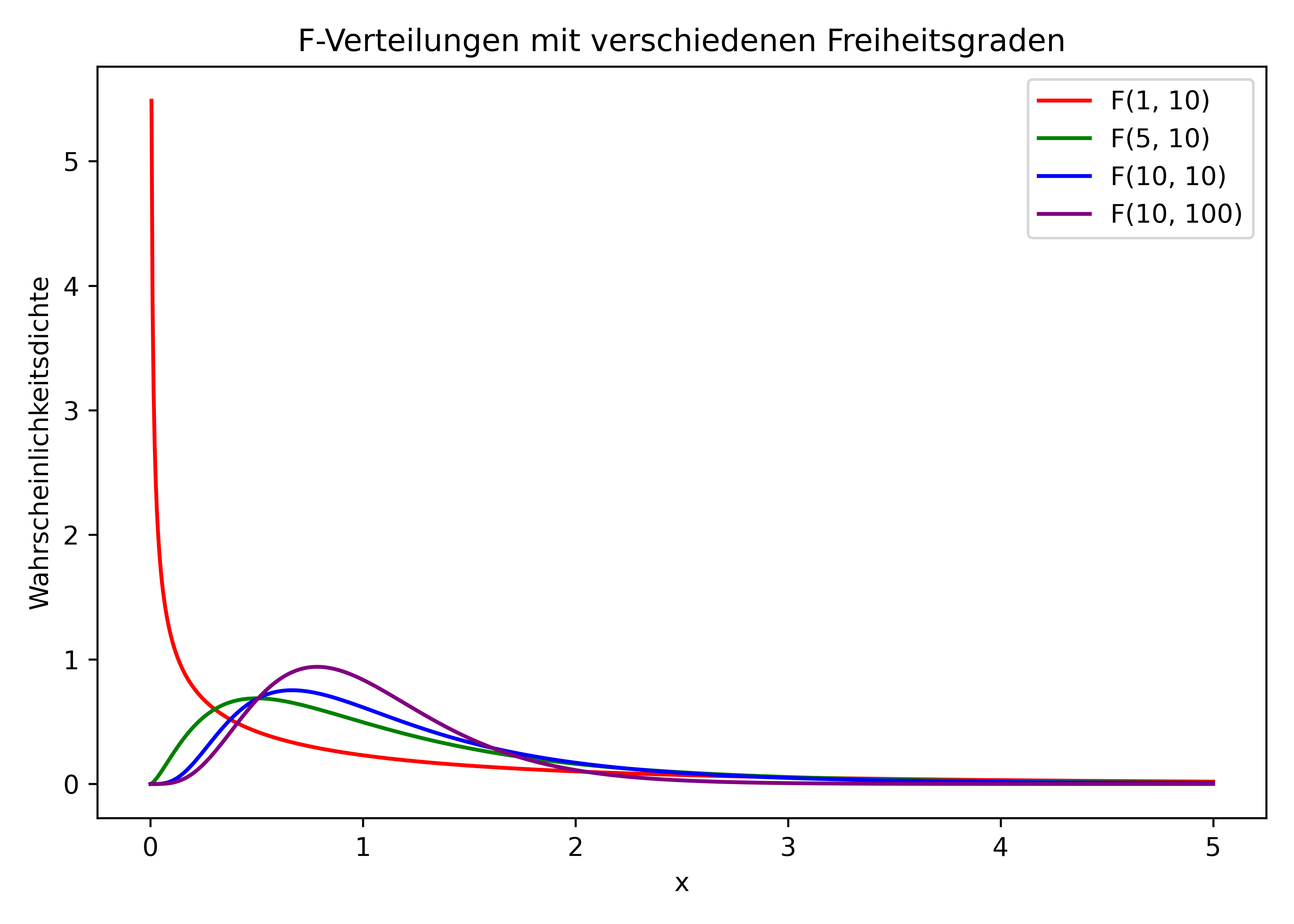
Die F-Verteilung wird hauptsächlich in der Varianzanalyse (ANOVA) verwendet, um Verhältnisse von Varianzen zu vergleichen. Sie hat zwei Freiheitsgrade-Parameter.
Binomialverteilung
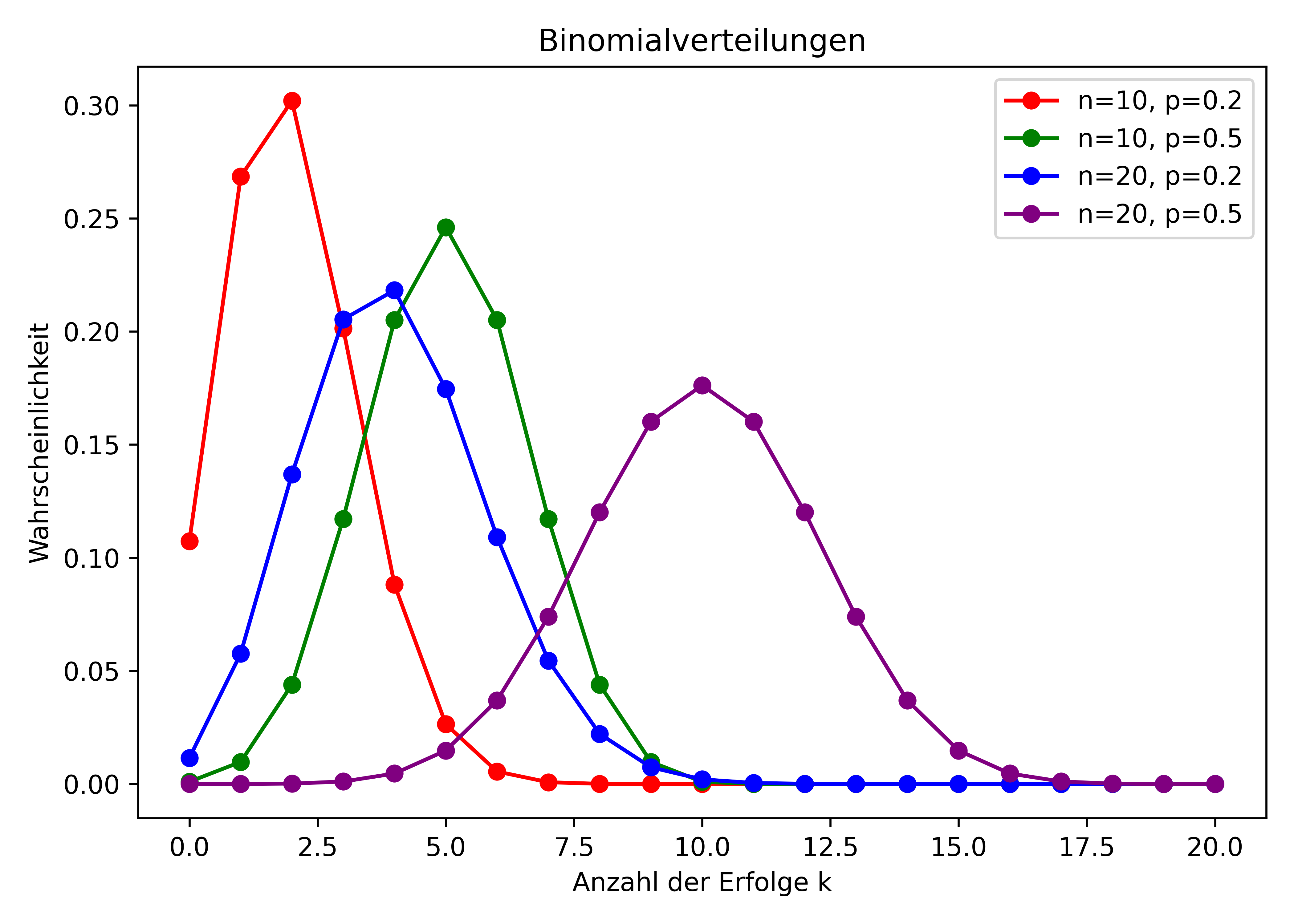
Die Binomialverteilung modelliert die Anzahl der Erfolge in einer festen Anzahl von unabhängigen Versuchen mit der gleichen Erfolgswahrscheinlichkeit (z.B. Anzahl der Köpfe beim Münzwurf).
Poisson-Verteilung
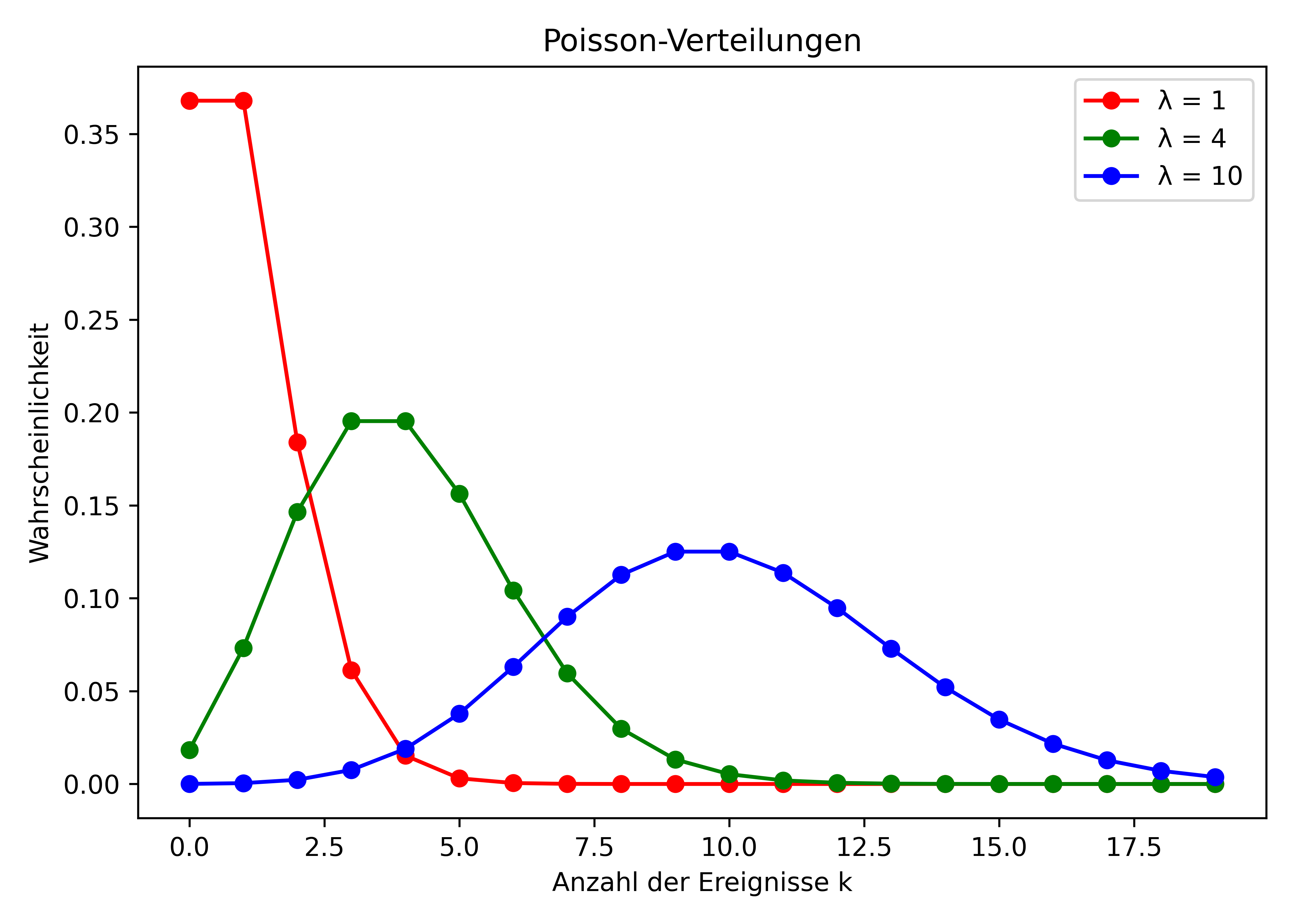
Die Poisson-Verteilung modelliert die Anzahl von Ereignissen, die in einem festen Zeitintervall auftreten, wenn diese Ereignisse mit einer bekannten konstanten Rate und unabhängig voneinander auftreten (z.B. Anzahl der Anrufe pro Stunde in einem Call-Center).
Relevanz dieser Verteilungen für Konfidenzintervalle
Jede dieser Verteilungen hat ihre spezifische Anwendung bei der Berechnung von Konfidenzintervallen:
- t-Verteilung: Für Konfidenzintervalle des Mittelwerts bei kleinen Stichproben (typischerweise n < 30).
- Chi-Quadrat-Verteilung: Für Konfidenzintervalle der Varianz oder Standardabweichung.
- F-Verteilung: Für Konfidenzintervalle des Verhältnisses zweier Varianzen.
- Binomial- und Poisson-Verteilung: Für Konfidenzintervalle von Anteilen bzw. Raten.
Die Wahl der richtigen Verteilung für ein Konfidenzintervall hängt davon ab, welchen Parameter wir schätzen und welche Annahmen wir über die Daten treffen können.
Zusammenfassung
In diesem Kapitel haben wir Konfidenzintervalle als wesentliche Ergänzung zur statistischen Inferenz kennengelernt. Im Gegensatz zu p-Werten, die nur angeben, ob ein Effekt statistisch signifikant ist, bieten Konfidenzintervalle wichtige zusätzliche Informationen:
Von Punkt- zu Intervallschätzungen: Wir haben den Unterschied zwischen einer Punktschätzung (z.B. der Korrelationskoeffizient r) und einer Intervallschätzung (Konfidenzintervall) kennengelernt. Konfidenzintervalle quantifizieren die Unsicherheit unserer Schätzungen.
Interpretation von Konfidenzintervallen: Ein 95%-Konfidenzintervall bedeutet, dass bei wiederholter Stichprobenziehung etwa 95% der konstruierten Intervalle den wahren Populationsparameter enthalten würden – nicht, dass der Parameter mit 95% Wahrscheinlichkeit im Intervall liegt.
-
Komponenten eines Konfidenzintervalls: Jedes Konfidenzintervall besteht aus drei Komponenten:
- Punktschätzung (z.B. Stichprobenmittelwert)
- Kritischer Wert (z.B. aus der t-Verteilung für ein 95%-KI)
- Standardfehler der Schätzung
Normalverteilung: Als wichtigste Wahrscheinlichkeitsverteilung in der Statistik ist die Normalverteilung Grundlage vieler Konfidenzintervalle. Mit der 68-95-99,7-Regel haben wir eine nützliche Faustregel kennengelernt.
Freiheitsgrade und t-Verteilung: Wir haben verstanden, was Freiheitsgrade sind und warum wir bei kleinen Stichproben die t-Verteilung statt der Normalverteilung verwenden müssen, um die zusätzliche Unsicherheit zu berücksichtigen.
Standardfehler vs. Standardabweichung: Der Standardfehler ist ein Maß für die Genauigkeit einer Schätzung und nimmt mit steigender Stichprobengröße ab (proportional zu 1/√n). Die Standardabweichung hingegen beschreibt die Streuung der einzelnen Datenpunkte.
Effekt der Stichprobengröße: Mit zunehmender Stichprobengröße werden Konfidenzintervalle schmaler, was eine präzisere Schätzung des Populationsparameters ermöglicht.
Andere Wahrscheinlichkeitsverteilungen: Je nach Anwendungsfall können auch andere Verteilungen wie die Chi-Quadrat-Verteilung, F-Verteilung oder diskrete Verteilungen wie die Binomial- und Poisson-Verteilung relevant sein.
Konfidenzintervalle bieten gegenüber p-Werten mehrere Vorteile: Sie geben Informationen über die Effektstärke und deren Spannweite, zeigen die Präzision der Schätzung und sind oft intuitiver zu interpretieren. Dies macht sie zu einem unverzichtbaren Werkzeug in der statistischen Analyse, besonders wenn es um die Kommunikation von Ergebnissen und evidenzbasierte Entscheidungsfindung geht.
- The Shape of Data: Distributions: Crash Course Statistics #7
- Binomialverteilung vs. Normalverteilung
- Was ist ein Vertrauensintervall / Konfidenzintervall?
- Standard Deviation vs Standard Error, Clearly Explained!!!
- What is a random variable?
- What is a statistic?
- Statistik: t-Verteilung und Freiheitsgrade
Optional:
- t-Verteilung, Unterschied zu z-Verteilung, Student-t-Verteilung, Mathe by Daniel Jung
- t-Verteilung und Freiheitsgrade (Degrees of Freedom), Mathe by Daniel Jung
- Explaining Probability Distributions | VNT #1
- Understand The Normal Distribution and Central Limit Theorem | VNT #3
- Explaining Confidence Intervals and The Critical Region | VNT #6
Übungen
Übung 1
Berechne 80%-, 95%- und 99%-Konfidenzintervalle für den Mittelwert der Körpergröße basierend auf der mittleren Stichprobe (heights_medium). Vergleiche die Breite der Intervalle. Was fällt dir auf?
Fällt dir eine Möglichkeit ein, wie du alle drei Konfidenzintervalle für denselben Mittelwert gemeinsam visualisieren kannst? Erzeuge eine Abbildung, bei der auf der x-Achse die drei Stichproben sind und auf der y-Achse die Körpergröße. Bis hierhin entspräche dies der Abbildung am Ende vom Abschnitt “Standardfehler (vs. Standardabweichung)”. Dort wurden allerdings mittels Fehlerbalken nur die 95%-Konfidenzintervalle dargestellt. Erzeuge eine Abbildung, bei der alle drei Konfidenzintervalle dargestellt werden - für alle drei Stichproben.
Bonus: Schließlich kann zum Vergleich noch zusätzlich die Standardabweichung der Körpergrößen in der Abbildung dargestellt werden.