import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
import statsmodels.api as sm
import statsmodels.formula.api as smfEinfache Lineare Regression
Im vorherigen Kapitel haben wir uns mit der Korrelation und somit mit Möglichkeiten beschäftigt, Zusammenhänge zwischen Variablen zu beschreiben. In diesem Kapitel werden wir einen Schritt weitergehen und uns mit linearen Modellen beschäftigen – einer der grundlegendsten und gleichzeitig mächtigsten Methoden der statistischen Analyse.
Was ist lineare Regression?
Die lineare Regression ist ein statistisches Verfahren, das den Zusammenhang zwischen einer abhängigen Variable und einer oder mehreren unabhängigen Variablen durch eine lineare Funktion (eine Gerade) modelliert. Im einfachsten Fall, der einfachen linearen Regression, beschreiben wir die Beziehung zwischen zwei numerischen Variablen.
Stellt euch einen Scatterplot vor, in dem Punkte verstreut sind. Die lineare Regression findet die beste Gerade, die durch diese Punktwolke verläuft.
Das mathematische Modell hinter einer solchen Geraden ist:
\[y = \alpha + \beta x + \varepsilon\]
Dabei ist:
- \(y\) die abhängige Variable (a.k.a. Zielvar., Outcome, Response Var., Dependent Var., Regressand, Target, Label, Output)
- \(x\) die unabhängige Var. (a.k.a. Prädiktor, erklärende Var., Einflussgröße, Independent Var., Regressor, Explanatory Var., Feature, Input, Covariate, Predictor)
- \(\alpha\) der y-Achsenabschnitt (a.k.a. Intercept, Schnittpunkt mit y-Achse, Konstante, Constant Term, Bias Term, Offset)
- \(\beta\) die Steigung (a.k.a. Slope, Regressionskoeffizient, Regression Coefficient, Parameter, Weight, Model Parameter)
- \(\varepsilon\) der Fehlerterm (a.k.a. Residuum, Störterm, Error Term, Noise, Residual, Disturbance, Random Error)
Wie man sieht gibt es so einige Synonyme für die verschiedenen Begriffe. Das liegt u.a. daran, dass die lineare Regression in vielen verschiedenen Disziplinen verwendet wird. Im Machine Learning Context wird auch das Modell selbst oft stattdessen ausgedrückt als \(y = mx + c\), wobei \(m\) die Steigung und \(c\) der y-Achsenabschnitt ist und der Fehlerterm nicht explizit erwähnt wird.
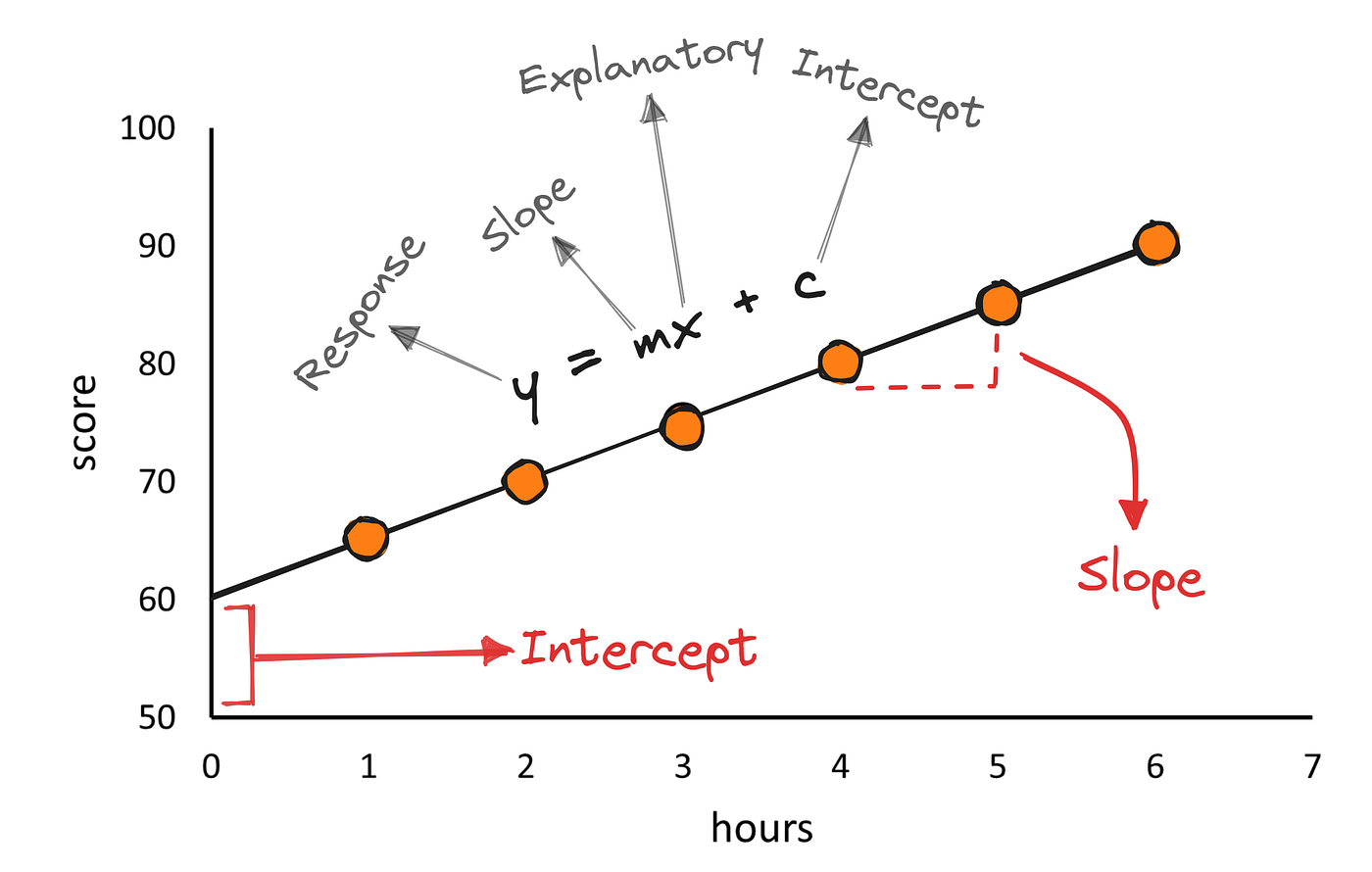Quelle: Dede Kurniawan
Interaktives Tool
Ich empfehle euch zumindest kurz z.B. mit diesem Tool zu experimentieren, um ein Gefühl für die einfache lineare Regression zu bekommen. Einfach dem Link folgen, dann in die Zelle oben links y=a+bx eintippen und mit Enter bestätigen. Dann könnt ihr die Werte für \(a\) und \(b\) mit einem Schieberegler anpassen und sehen, wie sich die Gerade verändert.
Abhängige vs. unabhängige Variablen
Im Gegensatz zur Korrelation, bei der beide Variablen gleichwertig betrachtet werden (bzw. austauschbar sind), unterscheiden wir bei der Regression explizit zwischen:
- Abhängige Variable: Die Variable, die wir vorhersagen oder erklären möchten.
- Unabhängige Variable(n): Die Variable(n), die wir zur Vorhersage verwenden.
Man nennt die Regression auch ein gerichtetes Modell.
Ein Beispiel
Wir werden nun die lineare Regression anhand der Beziehung zwischen Alkoholkonsum und Blutalkoholkonzentration (Promille) in einem fiktiven Datensatz demonstrieren.
Der Datensatz
# Daten via URL importieren
pfad = "https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/drinks/drinks.csv"
dat = pd.read_csv(pfad)
dat Person drinks blood_alc
0 Max 1 0.2
1 Max 2 0.3
2 Max 3 0.5
3 Max 3 0.6
4 Max 4 0.6
5 Max 4 0.5
6 Max 4 0.7
7 Max 5 0.6
8 Max 7 0.8
9 Max 8 1.0
10 Peter 1 0.1
11 Peter 1 0.1
12 Peter 1 0.2
13 Peter 1 0.2
14 Peter 1 0.1
15 Peter 3 0.3
16 Peter 5 0.5
17 Peter 6 0.8
18 Peter 8 0.9
19 Peter 9 1.3Unser Datensatz enthält Messungen von zwei Personen (Max und Peter), bei denen die Anzahl der konsumierten Getränke (drinks) und der resultierende Blutalkoholspiegel (blood_alc) erfasst wurden. Es sei aber direkt betont, dass wir uns nicht für die zwei Personen interessieren, sondern für die Beziehung zwischen den beiden numerischen Variablen. Anstatt die Daten nur als Tabelle zu betrachten, sollten wir sie natürlich auch visualisieren:
fig, ax = plt.subplots()
ax.scatter(dat['drinks'], dat['blood_alc'], color='blue', s=80)
ax.set_xlabel('Anzahl der Getränke')
ax.set_ylabel('Promille [‰]')
plt.show()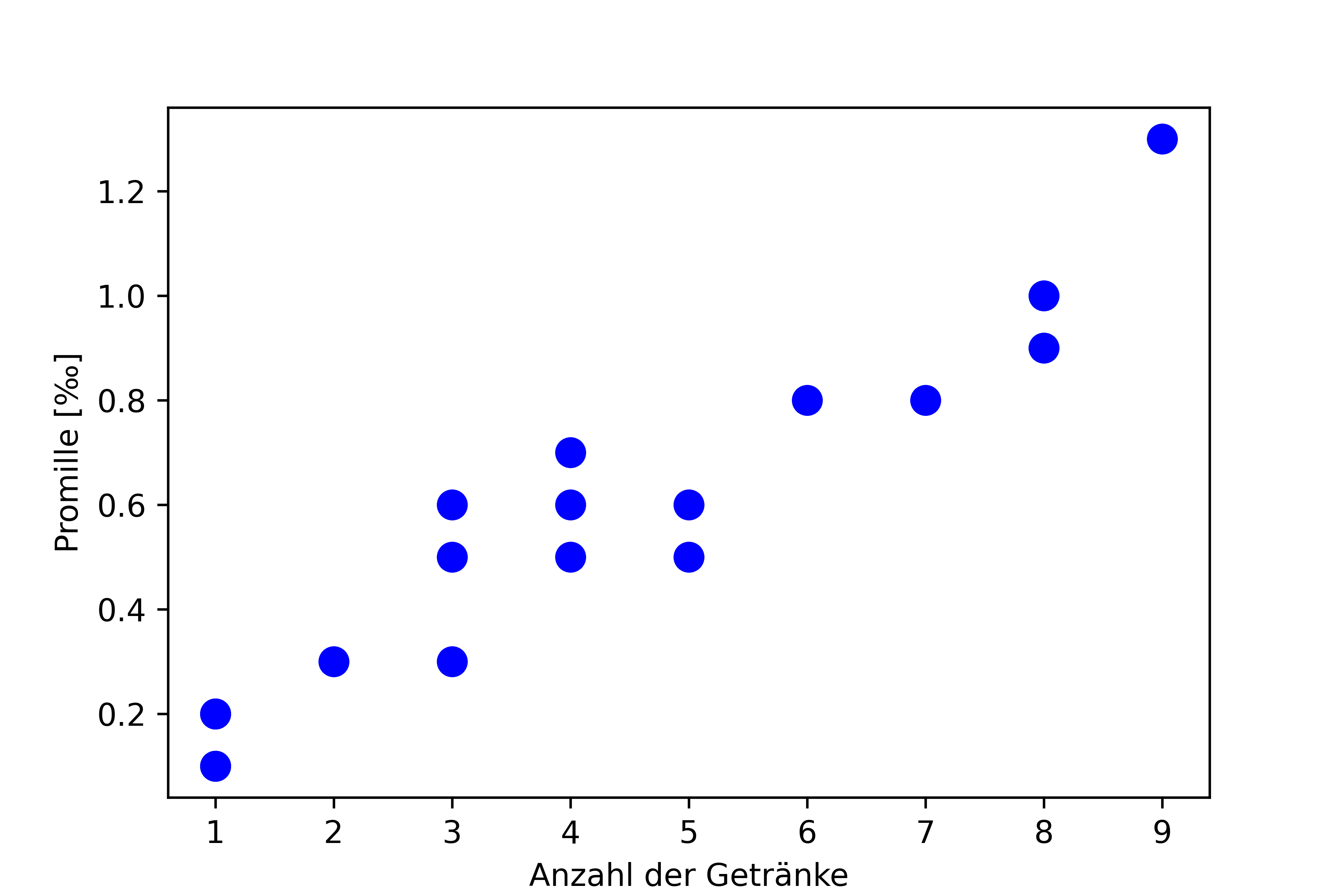
Bei der Betrachtung dieses Plots sehen wir bereits einen offensichtlichen Trend: Mit zunehmender Anzahl der Getränke steigt der Blutalkoholspiegel. Dies erscheint intuitiv sinnvoll. Und übrigens könnten wir an dieser Stelle auch die Korrelation berechnen, um den Zusammenhang quantitativ zu beschreiben. Achtung: Einige Punkte liegen direkt aufeinander, da identische Messwerte vorliegen.
Implementierung in Python
In Python können wir eine lineare Regression mit verschiedenen Modulen durchführen. In diesem Kapitel werden wir zwei gängige Ansätze kennenlernen:
- Verwendung von
scikit-learn, einer umfassenden Machine-Learning-Modul - Verwendung von
statsmodels, einer Modul für statistische Modelle
Beide Analysen führen zum gleichen Ergebnis für unsere Parameter:
- Intercept (α): etwa 0.049
- Steigung (β): etwa 0.121
Das bedeutet, dass unser geschätztes Modell wie folgt aussieht und in das man nun also manuell eine Zahl für die Anzahl der Getränke einsetzen kann, um den Blutalkoholspiegel vorherzusagen:
\[\text{blood\_alc} = 0.049 + 0.121 \times \text{drinks}\]
scikit-learn
# Vorbereitung der Daten für sklearn
X = dat[['drinks']].values # Unabhängige Variable(n) - immer als 2D-Array
y = dat['blood_alc'].values # Abhängige Variable
mod_sklearn = LinearRegression().fit(X, y)
print(f"Intercept (α): {mod_sklearn.intercept_:.4f}")
print(f"Steigung (β): {mod_sklearn.coef_[0]:.4f}")Intercept (α): 0.0490
Steigung (β): 0.1210Bei sklearn übergeben wir unsere unabhängige Variable immer als 2D-Array (daher die doppelten eckigen Klammern) und unsere abhängige Variable als 1D-Array.
statsmodels
mod_statsmodels = smf.ols(formula='blood_alc ~ drinks', data=dat).fit()
print(f"Intercept (α): {mod_statsmodels.params[0]:.4f}")
print(f"Steigung (β): {mod_statsmodels.params[1]:.4f}")Intercept (α): 0.0490
Steigung (β): 0.1210Bei der Formel-Syntax von statsmodels geben wir die Beziehung zwischen den Variablen in Form einer Formel an: abhängige_variable ~ unabhängige_variable. Dabei entspricht die Tilde (~) dem mathematischen Gleichheitszeichen der Formel und einen Achsenabschnitt muss man nicht angeben, da dieser standardmäßig hinzugefügt wird. Schließlich braucht man auch nur den Namen der abhängigen Variable zu schreiben, da diese - ebenfalls standardmäßig - mit einer zu schätzen Steigung multipliziert wird. So übersetzt sich demnach y ~ x standardmäßig zu \(y = \alpha + \beta x\), solange x numerisch ist. Die Formel-Syntax ist besonders nützlich, wenn wir mit mehreren Variablen arbeiten oder Interaktionen zwischen Variablen berücksichtigen möchten. Sie ist auch sehr leserlich und intuitiv.
Ein weiterer Vorteil ist, dass wir direkt auf die Spalten des DataFrames zugreifen können, ohne die Daten vorher umzuwandeln.
Alternative Syntax in statsmodels
Neben der Formel-Syntax unterstützt statsmodels auch einen alternativen Ansatz, der mehr dem sklearn-Ansatz ähnelt:
# Daten vorbereiten
X_sm = sm.add_constant(dat['drinks']) # Konstante (Intercept) hinzufügen
mod_statsmodels_2 = sm.OLS(dat['blood_alc'], X_sm).fit()
# Parameter ausgeben
print(f"Intercept (α): {mod_statsmodels_2.params[0]:.4f}")
print(f"Steigung (β): {mod_statsmodels_2.params[1]:.4f}")Intercept (α): 0.0490
Steigung (β): 0.1210Der Unterschied zum sklearn-Ansatz ist, dass wir bei statsmodels mit add_constant() explizit eine Spalte für den Intercept hinzufügen müssen, während sklearn dies automatisch macht, wenn fit_intercept=True (Standard) ist.
Wenn wir detailliertere statistische Informationen benötigen, bietet statsmodels eine umfassende Zusammenfassung:
# Ausführliche Zusammenfassung des Modells
print(mod_statsmodels.summary()) OLS Regression Results
==============================================================================
Dep. Variable: blood_alc R-squared: 0.914
Model: OLS Adj. R-squared: 0.909
Method: Least Squares F-statistic: 190.8
Date: Di, 19 Aug 2025 Prob (F-statistic): 5.09e-11
Time: 11:43:23 Log-Likelihood: 18.546
No. Observations: 20 AIC: -33.09
Df Residuals: 18 BIC: -31.10
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.0490 0.041 1.206 0.243 -0.036 0.134
drinks 0.1210 0.009 13.811 0.000 0.103 0.139
==============================================================================
Omnibus: 1.154 Durbin-Watson: 1.607
Prob(Omnibus): 0.562 Jarque-Bera (JB): 1.057
Skew: 0.442 Prob(JB): 0.589
Kurtosis: 2.302 Cond. No. 8.60
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Diese Zusammenfassung enthält wichtige Statistiken (die bisher nur teilweise eingeführt wurden):
- Bestimmtheitsmaß: R² und adjustiertes R²
- F-Statistik und deren p-Wert
- Standardfehler und p-Werte für jede Schätzung
- Konfidenzintervalle
- Verschiedene Diagnosetests
Visualisierung des Regressionsmodells
Ein zentraler Vorteil der Regression gegenüber der bloßen Korrelation ist die Möglichkeit, Vorhersagen (auch genannt: Prädiktionen, Schätzungen, Erwartungswerte) zu treffen. Die Regressionsgerade ist nichts anderes als eine grafische Darstellung dieser Vorhersagen - jeder Punkt auf der Linie entspricht einer Vorhersage eines Modells für den entsprechenden x-Wert. Um die Linie einzuzeichnen, müssen wir demnach unser bereits fertig angepasstes Modell nutzen um Vorhersagen zu machen:
# x-Werte für die das Modell Vorhersagen machen soll
x_pred = np.arange(dat['drinks'].min(), dat['drinks'].max()+1)
# Option 1: Vorhersagen mit dem sklearn-Modell
y_pred = mod_sklearn.predict(x_pred.reshape(-1, 1))
# Option 2: Vorhersagen mit dem statsmodels-Modell
y_pred = mod_statsmodels.predict(pd.DataFrame({'drinks': x_pred}))
# Hinzufügen der Regressionsgerade
fig, ax = plt.subplots()
ax.scatter(dat['drinks'], dat['blood_alc'], color='blue', s=80)
ax.plot(x_pred, y_pred, color='green', linewidth=2)
ax.set_xlabel('Anzahl der Getränke')
ax.set_ylabel('Promille [‰]')
plt.show()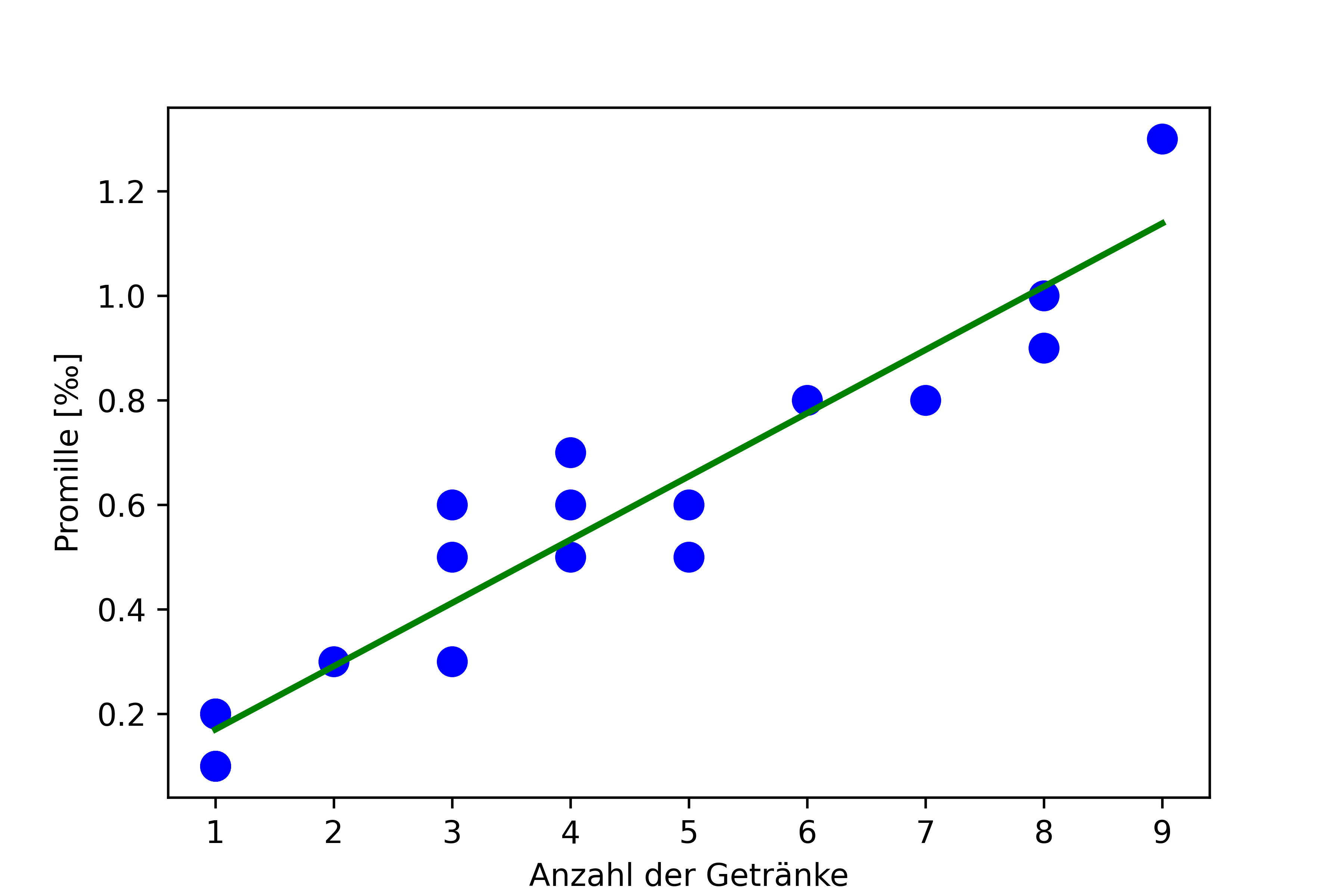
- Die Variable
x_predenthält dabei nicht selbst Vorhersagen, sondern die x-Werte, für die wir Vorhersagen machen wollen. Wir wählen dabei einfach alle x-Werte vom kleinsten bis größten Wert in unseren Daten. -
Nicht vergessen: bei
np.arange()ist der Endwert (zweiter Parameter) nicht inklusiv - die Range geht nur bis einen vor dem angegebenen Wert. Deshalb addieren wir +1, um sicherzustellen, dass auch der maximale x-Wert in unseren Daten eingeschlossen ist. - Für die Vorhersage mit scikit-learn müssen die x-Werte als 2D-Array vorliegen (auch wenn es nur eine Spalte gibt). Die Methode
reshape(-1, 1)wandelt unser 1D-Array in die erforderliche Form um. - Statsmodels hingegen erwartet die Daten in einem DataFrame mit den gleichen Spaltennamen, die bei der Modellerstellung verwendet wurden - hier ‘drinks’.
Residuen: Die Differenz zwischen Modell und Realität
Mit unserem geschätzten Modell können wir also Vorhersagen für beliebige Werte der unabhängigen Variable machen. Besonders interessant ist aber zunächst eine Vorhersage für genau die x-Werte, die bereits in unseren Daten vorkommen. Dies ermöglicht uns, die vorhergesagten Werte mit den tatsächlich beobachteten Werten zu vergleichen:
# Vorhersagen
dat['blood_alc_pred'] = mod_sklearn.predict(dat['drinks'].values.reshape(-1, 1)) # sklearn
dat['blood_alc_pred'] = mod_statsmodels.predict(dat) # statsmodels
# Residuen
dat['residual'] = dat['blood_alc'] - dat['blood_alc_pred'] # Manuell = sklearn
dat['residual'] = mod_statsmodels.resid # statsmodels
dat Person drinks blood_alc blood_alc_pred residual
0 Max 1 0.2 0.170011 0.029989
1 Max 2 0.3 0.291060 0.008940
2 Max 3 0.5 0.412109 0.087891
3 Max 3 0.6 0.412109 0.187891
4 Max 4 0.6 0.533157 0.066843
5 Max 4 0.5 0.533157 -0.033157
6 Max 4 0.7 0.533157 0.166843
7 Max 5 0.6 0.654206 -0.054206
8 Max 7 0.8 0.896303 -0.096303
9 Max 8 1.0 1.017352 -0.017352
10 Peter 1 0.1 0.170011 -0.070011
11 Peter 1 0.1 0.170011 -0.070011
12 Peter 1 0.2 0.170011 0.029989
13 Peter 1 0.2 0.170011 0.029989
14 Peter 1 0.1 0.170011 -0.070011
15 Peter 3 0.3 0.412109 -0.112109
16 Peter 5 0.5 0.654206 -0.154206
17 Peter 6 0.8 0.775255 0.024745
18 Peter 8 0.9 1.017352 -0.117352
19 Peter 9 1.3 1.138401 0.161599Wir sehen nun für jeden Datenpunkt den beobachteten Wert blood_alc, den vom Modell vorhergesagten Wert blood_alc_pred und die Differenz zwischen beiden (das Residuum; residual). Ein positives Residuum bedeutet, dass der beobachtete Wert größer als der vorhergesagte Wert ist - das Modell unterschätzt also den tatsächlichen Wert. Ein negatives Residuum bedeutet entsprechend, dass der beobachtete Wert kleiner als der vorhergesagte Wert ist - das Modell überschätzt den tatsächlichen Wert.
Residuen sind ein wichtiges Konzept in allen statistischen Modellen, nicht nur in der Regression. Sie helfen uns zu verstehen, wie gut unser Modell die Daten beschreibt und ob es systematische Fehler gibt. Wie gesgat ist ein Residuum die Differenz zwischen dem beobachteten Wert und dem vom Modell vorhergesagten Wert:
\[\text{Residuum} = y_{\text{beobachtet}} - y_{\text{vorhergesagt}}\]
Die Residuen geben uns Aufschluss darüber, wie gut unser Modell die Daten beschreibt. Lassen wir uns die Residuen visualisieren:
fig, ax = plt.subplots()
# Scatterplot mit Regressionsgerade
ax.scatter(dat['drinks'], dat['blood_alc'],
color='blue', s=80, label='Beobachtet', zorder=3)
ax.scatter(dat['drinks'], dat['blood_alc_pred'],
color='green', s=40, label='Vorhergesagt', zorder=4)
ax.plot(x_pred, y_pred,
color='green', linewidth=2, label='Regressionsgerade', zorder=2)
# Residuen als vertikale Linien einzeichnen
for i in range(len(dat)):
ax.plot([dat['drinks'][i], dat['drinks'][i]],
[dat['blood_alc_pred'][i], dat['blood_alc'][i]],
color='red', zorder=5)
ax.set_title('Visualisierung der Residuen')
ax.set_xlabel('Anzahl der Getränke')
ax.set_ylabel('Promille [‰]')
ax.legend()
plt.show()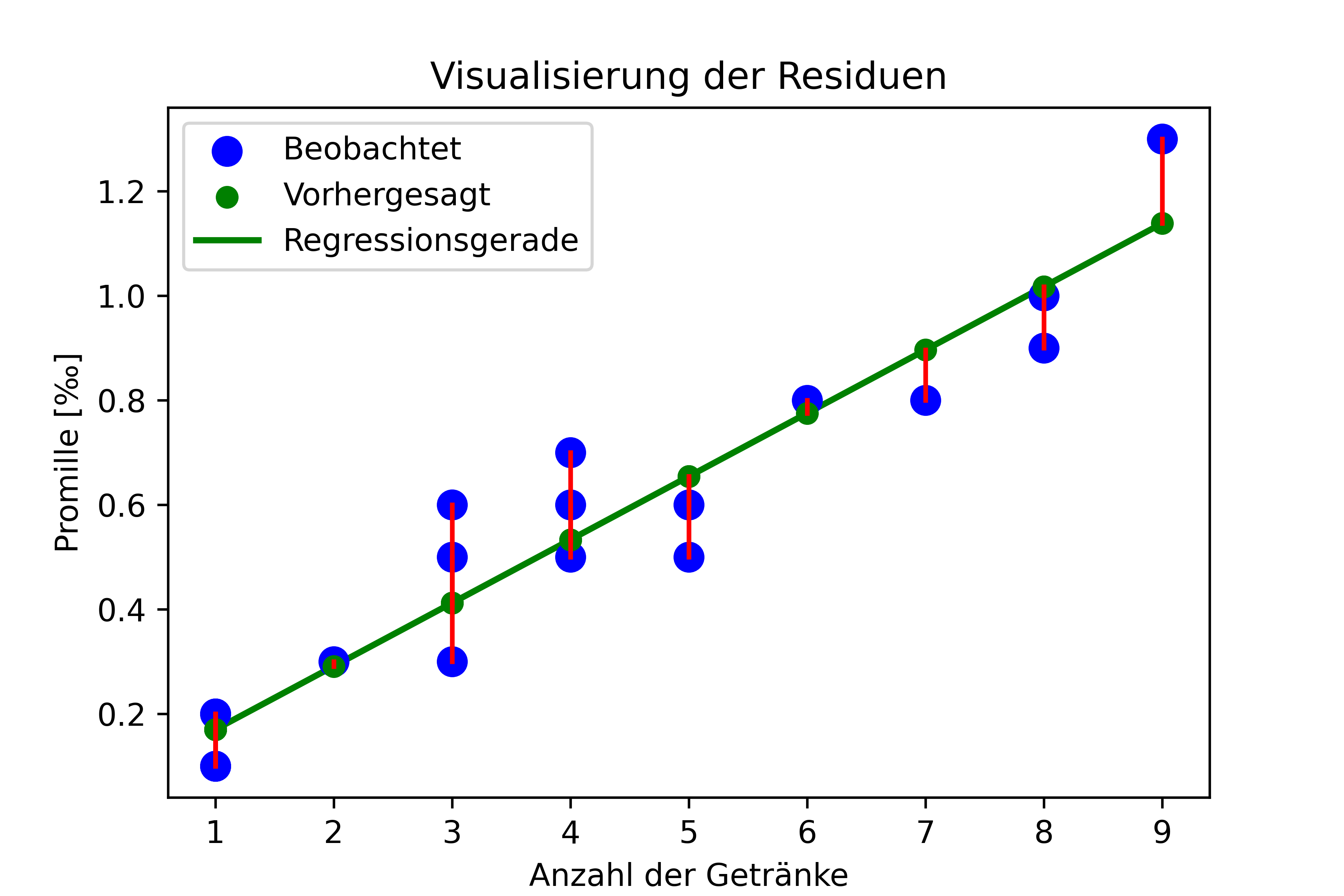
In dieser Visualisierung:
- Die blauen Punkte stellen die beobachteten Werte dar
- Die grüne Linie ist unsere Regressionsgerade mit den vorhergesagten Werten
- Die grünen Punkte sind dann zusätzlich genau die Punkte auf der Regressionsgerade, die zu den beobachteten Werten gehören
- Die roten gestrichelten Linien zeigen die Residuen - also die vertikalen Abstände zwischen den beobachteten Werten und der Regressionslinie
Die Länge jeder roten Linie entspricht dem Betrag des Residuums für den entsprechenden Datenpunkt. Je größer die Residuen sind, desto schlechter passt unser Modell zu den Daten.
Loss-Funktionen und OLS
Wie bestimmt man eigentlich die “beste” Regressionsgerade? Was haben sklearn und statsmodels gemacht, um die Parameter \(\alpha\) und \(\beta\) zu schätzen? Hier kommen Loss-Funktionen (Verlustfunktionen, Kostenfunktionen) ins Spiel. Sie quantifizieren, wie gut oder schlecht unser Modell die Daten beschreibt.
Die in der linearen Regression am häufigsten verwendete Loss-Funktion ist die Summe der quadrierten Residuen (Sum of Squared Residuals, SSR), auch bekannt als Ordinary Least Squares (OLS):
\[\text{SSR} = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \sum_{i=1}^{n} (y_i - (\alpha + \beta x_i))^2\]
Der Algorithmus sucht nach den Werten für \(\alpha\) und \(\beta\), die diese Summe minimieren. Daher der Name “Least Squares” (kleinste Quadrate).
Es gibt verschiedene Varianten von Loss-Funktionen, die in unterschiedlichen Situationen nützlich sein können.
- SSR (Sum of Squared Residuals): Summe der quadrierten Residuen
- MSE (Mean Squared Error): Durchschnitt der quadrierten Residuen
- MAE (Mean Absolute Error): Durchschnitt der absoluten Residuen
- RMSE (Root Mean Squared Error): Wurzel aus dem MSE
- Huber Loss: Kombination aus MSE für kleine Residuen und MAE für große Residuen, weniger empfindlich gegenüber Ausreißern
Die Wahl der Loss-Funktion beeinflusst z.B., wie stark Ausreißer das Modell beeinflussen. MSE bestraft große Abweichungen stärker als MAE, da die Abweichungen quadriert werden. Diese Maße für genau unsere Residuen aus unserem Modell zu berechnen ist einfach:
residuals = dat['residual'].values
# Manuelle Berechnung der Summe der quadrierten Residuen
ssr = np.sum(residuals**2)
print(f"Summe der quadrierten Residuen (SSR): {ssr:.4f}")
# Mittlere quadratische Abweichung (MSE = Mean Squared Error)
mse = np.mean(residuals**2)
print(f"Mittlere quadratische Abweichung (MSE): {mse:.4f}")
# Mittlere absolute Abweichung (MAE = Mean Absolute Error)
mae = np.mean(np.abs(residuals))
print(f"Mittlere absolute Abweichung (MAE): {mae:.4f}")
# Wurzel aus der mittleren quadratischen Abweichung (RMSE = Root Mean Squared Error)
rmse = np.sqrt(mse)
print(f"Wurzel aus der mittleren quadratischen Abweichung (RMSE): {rmse:.4f}")Summe der quadrierten Residuen (SSR): 0.1833
Mittlere quadratische Abweichung (MSE): 0.0092
Mittlere absolute Abweichung (MAE): 0.0795
Wurzel aus der mittleren quadratischen Abweichung (RMSE): 0.0957Was “der Algorithmus” allerdings genau tut, damit wir optimale Parameterschätzungen erhalten, ist der eigentliche Clou.
Für die “normale” Regression (OLS) gibt es eine geschlossene mathematische Lösung, die auf Matrixalgebra basiert. Einfach ausgedrückt werden dafür die Daten in Matrizenform gepackt, miteinander multipliziert und invertiert, sodass schließlich die optimalen Werte für \(\alpha\) und \(\beta\) herauskommen. Wie schon bei der Korrelation gilt auch hier, dass man das auch mit Stift, Papier und Fleiß machen könnte.
Darüber hinaus gibt es aber auch andere Schätzverfahren, wie den Maximum-Likelihood-Ansatz. Er maximiert die Wahrscheinlichkeit, die beobachteten Daten unter Annahme normalverteilter Fehler zu erhalten, indem er iterativ verschiedene Parameterwerte ausprobiert.
Interessanterweise führen beide Ansätze - OLS und Maximum Likelihood - für lineare Regressionsmodelle mit normalverteilten Fehlern zum identischen Ergebnis.
Alternative Schätzverfahren - Kurzer Ausblick
In unserem Beispiel verwenden sowohl sklearn.LinearRegression als auch statsmodels.OLS die Ordinary Least Squares Methode mit der Summe der quadrierten Residuen (SSR) als Loss-Funktion. Diese spezifischen Klassen sind auf OLS spezialisiert und bieten keine direkte Möglichkeit, andere Schätzmethoden zu verwenden.
Allerdings bieten beide Modulen alternative Klassen für andere Schätzverfahren:
In scikit-learn kann man beispielsweise HuberRegressor für eine robustere Regression mit der Huber-Loss-Funktion verwenden, Ridge oder Lasso für regularisierte Regressionen oder RANSACRegressor für Regressionen, die besonders widerstandsfähig gegen Ausreißer sind.
Statsmodels bietet ebenfalls spezialisierte Klassen wie RLM für robuste lineare Modelle, WLS für gewichtete kleinste Quadrate oder GLM für verallgemeinerte lineare Modelle.
Die Wahl zwischen diesen Modulen und spezifischen Methoden hängt daher hauptsächlich davon ab, welches Schätzverfahren für das jeweilige Problem am besten geeignet ist und ob man eher eine einfache Modellimplementation (sklearn) oder eine umfassendere statistische Analyse (statsmodels) benötigt.
Bestimmtheitsmaß R2: Güte der Anpassung
Neben den Residuen können wir uns auch das sogenannte Bestimmtheitsmaß \(R^2\) (R-squared; Coefficient of Determination) anschauen, um die Güte der Anpassung unseres Modells zu bewerten. Es gibt an, wie gut unser Modell die Variation in den Daten erklärt und kann dabei Werte zwischen 0 und 1 annehmen. Ein Wert von 0 bedeutet, dass unser Modell die Daten nicht erklärt, während ein Wert von 1 bedeutet, dass unser Modell die Daten perfekt erklärt. Man kann in der Formel erkennen, dass oben die Summe der quadrierten Residuen steht (während unten die Summe der quadrierten Abweichungen vom Mittelwert steht):
\[R^2 = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2}\]
# R-Quadrat aus statsmodels-Zusammenfassung
print(f"R-Quadrat: {mod_statsmodels.rsquared:.4f}")R-Quadrat: 0.9138Ein R² von 0.91 bedeutet, dass etwa 91% der Varianz im Blutalkoholspiegel (in unseren Daten) durch die Anzahl der Getränke erklärt werden kann - ein ziemlich starker Zusammenhang!
Moment mal…
Bei unserer Regression haben wir ein Intercept (α) von etwa 0.049 geschätzt. Das bedeutet, dass unser Modell bei 0 Getränken einen Blutalkoholspiegel von 0.049 vorhersagt. Aber ist das sinnvoll? Sollte der Blutalkoholspiegel bei 0 Getränken nicht auch 0 sein?
Dieser Frage wollen wir aus zwei verschiedenen Perspektiven nachgehen.
Ist der Intercept wirklich nicht 0? (Statistik-Perspektive)
Zunächst sollten wir aus statistische Sicht prüfen, ob unser Ergebnise ernsthaft nahelegt, dass der Intercept von 0 verschieden ist. Dazu schauen wir uns den p-Wert und das Konfidenzintervall für den Intercept an. Wenn der p-Wert kleiner als unser Signifikanzniveau (z.B. 0.05) ist, können wir die Nullhypothese ablehnen und annehmen, dass der wahre Intercept signifikant von 0 verschieden ist. Das Konfidenzintervall gibt uns zusätzlich eine Vorstellung davon, in welchem Bereich wir den wahren Wert des Intercepts erwarten können.
# p-Wert für den Intercept aus dem statsmodels-Ergebnis
intercept_pvalue = mod_statsmodels.pvalues[0]
print(f"p-Wert für den Intercept: {intercept_pvalue:.4f}")
# Konfidenzintervall für den Intercept
conf_int = mod_statsmodels.conf_int().loc['Intercept']
print(f"95%-Konfidenzintervall für den Intercept: [{conf_int[0]:.4f}, {conf_int[1]:.4f}]")p-Wert für den Intercept: 0.2433
95%-Konfidenzintervall für den Intercept: [-0.0363, 0.1342]Der p-Wert für den Intercept ist 0.243, was größer als das übliche Signifikanzniveau von 0.05 ist. Das Konfidenzintervall für den Intercept schließt die 0 ein. Das bedeutet, dass wir nicht mit Sicherheit sagen können, dass der wahre Intercept von 0 verschieden ist.
Sicherlich ist unser Schätzwert von 0.049 trotzdem noch da und nicht gleich 0, aber das wird der Schätzwert auch nie sein - egal wie oft wir messen. Es gibt immer Zufall bzw. Rauschen in den Daten. Doch nun haben wir durch genaures Betrachten der Ergebnisse immerhin festgestellt, dass die Statistik also nicht wirklich dafür spricht, dass es in Wahrheit einen Intercept gibt.
Ein Modell ohne Intercept (Fachwissen-Perspektive)
Da wir uns so sicher sind, dass es biologisch gesehen keinen Intercept geben sollte, kommt die Frage auf warum wir überhaupt ein Modell mit Intercept verwendet haben. Man könnte quasi sagen, dass wir die Falsche Frage gestellt haben, als wir nach einer einfachen Regression gefragt haben.
Aus biologischer Sicht lässt sich durchaus argumentieren, dass ein Modell ohne Intercept sinnvoller ist, da der Blutalkoholspiegel bei 0 Getränken 0 sein muss. Wir können ein solches Modell (y = bx) sowohl mit scikit-learn als auch mit statsmodels anpassen:
# Modell ohne Intercept mit scikit-learn: fit_intercept=False
mod_sklean_noint = LinearRegression(fit_intercept=False).fit(X, y)
print(f"Steigung (β) ohne Intercept: {mod_sklean_noint.coef_[0]:.4f}")
# Modell ohne Intercept mit statsmodels: -1 + ...
mod_statsmodels_noint = smf.ols(formula='blood_alc ~ -1 + drinks', data=dat).fit()
print(mod_statsmodels_noint.summary())Steigung (β) ohne Intercept: 0.1298
OLS Regression Results
=======================================================================================
Dep. Variable: blood_alc R-squared (uncentered): 0.973
Model: OLS Adj. R-squared (uncentered): 0.972
Method: Least Squares F-statistic: 693.7
Date: Di, 19 Aug 2025 Prob (F-statistic): 2.03e-16
Time: 11:43:24 Log-Likelihood: 17.769
No. Observations: 20 AIC: -33.54
Df Residuals: 19 BIC: -32.54
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
drinks 0.1298 0.005 26.337 0.000 0.120 0.140
==============================================================================
Omnibus: 0.475 Durbin-Watson: 1.508
Prob(Omnibus): 0.789 Jarque-Bera (JB): 0.579
Skew: 0.177 Prob(JB): 0.749
Kurtosis: 2.245 Cond. No. 1.00
==============================================================================
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.Die Steigung (β) unseres Modells ohne Intercept beträgt etwa 0.1298, was etwas höher ist als beim Modell mit Intercept (0.1210). Das ergibt ja auch Sinn, da die Gerade nun sozusagen etwas weiter unten starten muss und trotzdem durch die gleichen Punkte laufen soll.
Visualisierung beider Modelle
Lassen wir uns beide Modelle visuell vergleichen (diesmal nur mit statsmodels):
fig, ax = plt.subplots(layout='tight')
ax.scatter(dat['drinks'], dat['blood_alc'], color='blue', s=80)
# Modell mit Intercept
ax.plot(x_pred,
mod_statsmodels.predict(pd.DataFrame({'drinks': x_pred})),
label=f'Mit Intercept (y = {mod_statsmodels.params[0]:.3f} + {mod_statsmodels.params[1]:.3f}x)',
color='green', linewidth=2)
# Modell ohne Intercept
ax.plot(x_pred,
mod_statsmodels_noint.predict(pd.DataFrame({'drinks': x_pred})),
label=f'Ohne Intercept (y = {mod_statsmodels_noint.params[0]:.3f}x)',
color='orange', linewidth=2)
ax.set_title('Vergleich: Regression mit und ohne Intercept')
ax.set_xlabel('Anzahl der Getränke')
ax.set_ylabel('Promille [‰]')
ax.legend()
plt.show()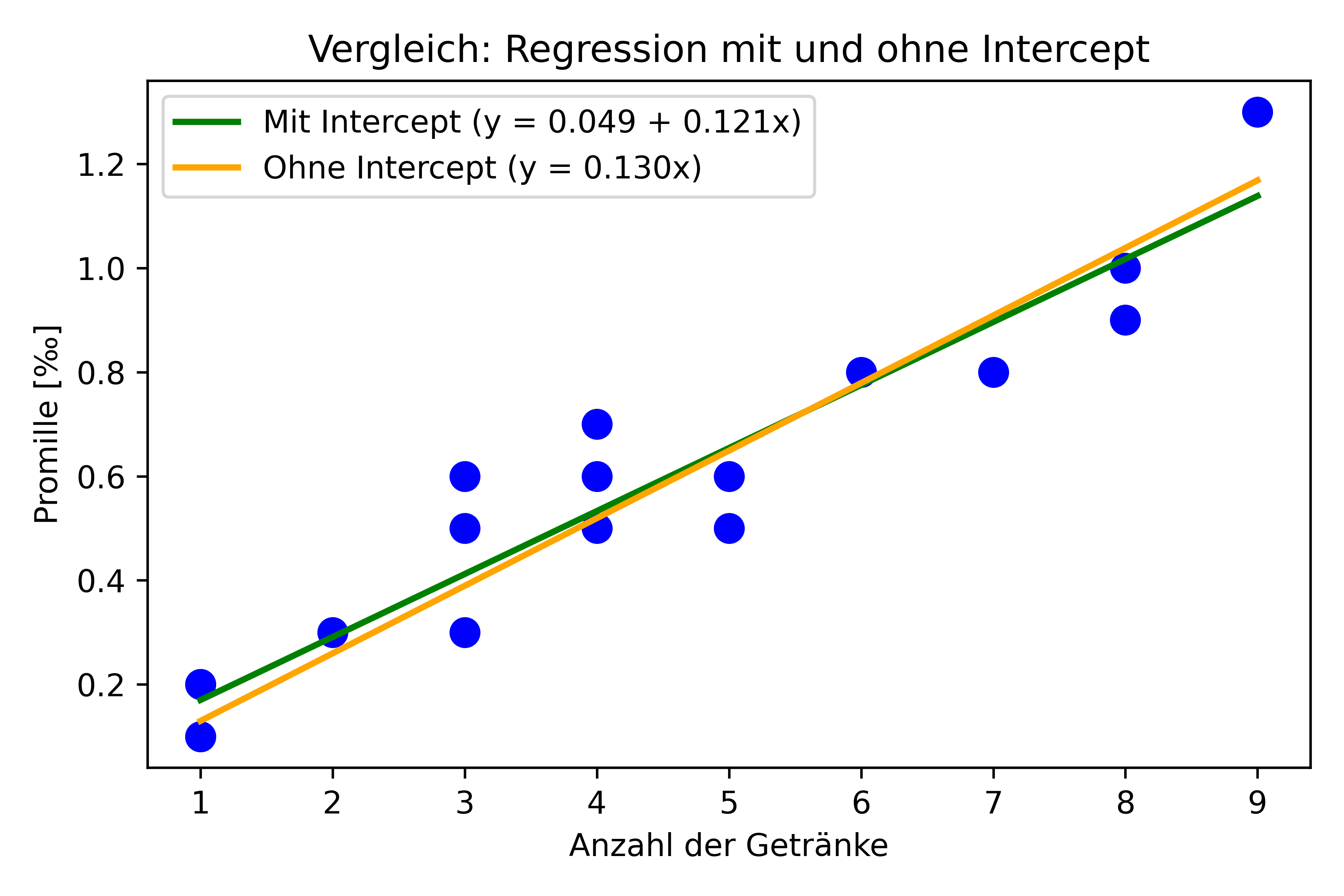
Welches Modell ist besser?
Die Entscheidung, ob ein Modell mit oder ohne Intercept verwendet werden sollte ist also nicht ohne Weiteres zu beantworten, sondern hängt vom spezifischen Kontext und der Fragestellung ab. In diesem Fall sprechen die statistischen Ergebnisse (nicht-signifikanter Intercept) und fachliche Überlegungen für das Modell ohne Intercept.
Zusammenfassung
In diesem Kapitel haben wir die Grundlagen der linearen Regression kennengelernt, einer der fundamentalsten und wichtigsten Methoden in der Statistik und im Machine Learning. Wir haben:
- Das mathematische Modell hinter der linearen Regression verstanden
- Den Unterschied zwischen abhängigen und unabhängigen Variablen erklärt
- Eine lineare Regression in Python mit scikit-learn und statsmodels implementiert
- Vorhersagen mit unserem Modell getroffen
- Das Konzept der Residuen und verschiedene Loss-Funktionen kennengelernt
- Die Frage des Intercepts diskutiert und ein alternatives Modell ohne Intercept erstellt
Die lineare Regression bildet die Grundlage für viele komplexere Modelle in der Statistik und im Machine Learning. In den nächsten Kapiteln werden wir auf diesem Wissen aufbauen und fortgeschrittenere Techniken wie multiple Regression und Regularisierungsmethoden kennenlernen.
Übungen
Übung 1
Führe separate lineare Regressionen für den gesamten Datensatz, nur für Max und nur für Peter durch. Erstelle dann einen DataFrame, der die Ergebnisse wie folgt zusammenfasst:
| Daten | Achsenabschnitt | P-Wert Achsenabschnitt | Steigung | P-Wert Steigung | R² |
|---|---|---|---|---|---|
| Gesamt | … | … | … | … | … |
| Max | … | … | … | … | … |
| Peter | … | … | … | … | … |
Übung 2
Erstelle ein Streudiagramm (Scatterplot) des Boston Housing Datensatzes, bei dem der Immobilienwert (MEDV) gegen die durchschnittliche Anzahl der Räume pro Wohnung (RM) aufgetragen wird. Führe eine lineare Regression durch und zeichne die Regressionsgerade in den Plot ein.
# Boston Housing Datensatz laden
pfad = "https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/boston_housing/boston_house_prices.csv"
boston = pd.read_csv(pfad, skiprows=1)Übung 3
Importiere den vision Datensatz und konzentriere dich auf die Spalten ages (Alter der Person) und vision (Sehstärke der Person von 0-10). Passe eine lineare Regression an und betrachte auch das Bestimmtheitsmaß. Wiederhole die Analyse, aber ohne die Person namens Rolando und vergleiche die Ergebnisse.
# Vision Datensatz laden
pfad = "https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/vision/vision_fixed.csv"
vision = pd.read_csv(pfad, sep=';')Hinweis: Lösungen zu den meisten Übungsaufgaben findet ihr, indem ihr ganz oben rechts im Kapitel auf den </> Code Button klickt und dann entsprechend nach ganz unten scrollt. Es ist Absicht, dass dies etwas umständlich ist.