import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import statsmodels.formula.api as smf
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_splitPolynomregression
In den vorherigen Kapiteln haben wir uns mit der einfachen und multiplen linearen Regression beschäftigt. Wir haben gesehen, wie wir eine abhängige Variable durch eine oder mehrere unabhängige Variablen vorhersagen können, wobei wir angenommen haben, dass die Beziehung zwischen diesen Variablen linear ist. Aber was ist, wenn die Beziehung zwischen den Variablen nicht linear ist?
Hier kommt die Polynomregression ins Spiel. Sie ist eine Erweiterung des linearen Regressionsmodells, die es uns ermöglicht, nicht-lineare Beziehungen zwischen Variablen zu modellieren, also einfach ausgedrückt: Kurven anstelle von Geraden.
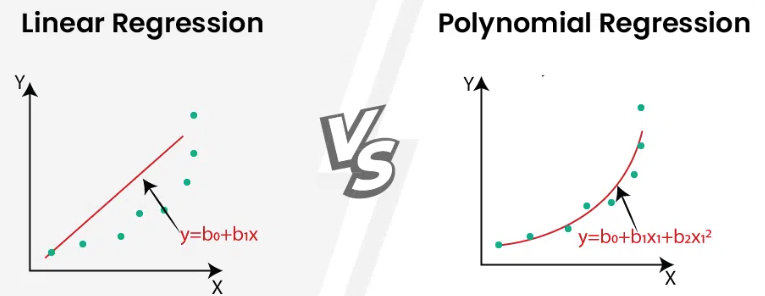
Quelle: GeeksForGeeks.org
Was bedeutet “linear” in “lineares Modell”?
Es gibt ein häufiges Missverständnis über die Bedeutung von “linear” in “lineares Modell”. Viele denken, dass ein lineares Modell nur lineare Beziehungen zwischen Variablen abbilden kann (also eine Gerade). Das ist jedoch nicht ganz richtig. Der Knackpunkt ist, dass das Wort “linear” sich hier jeweils auf unterschiedliche Dinge bezieht und dann auch unterschiedliche Bedeutungen hat.
- Eine Beziehung zwischen zwei Variablen ist linear, wenn sie durch eine Gerade dargestellt werden kann.
- Ein Modell ist linear, wenn es linear in seinen Parametern ist. Das bedeutet, dass die Parameter (die β-Koeffizienten) nicht in nicht-linearen Funktionen wie Exponenten, Logarithmen usw. auftauchen dürfen.
Betrachten wir folgende Modelle:
- \(y = \beta_0 + \beta_1 x + \varepsilon\) (einfache lineare Regression = Polynomregression 1. Grades)
- \(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \varepsilon\) (multiple lineare Regression, auch Polynomregression 1. Grades)
- \(y = \beta_0 + \beta_1 x + \beta_2 x^2 + \varepsilon\) (quadratische Regression = Polynomregression 2. Grades)
- \(y = \beta_0 + \beta_1 x + \beta_2 x^2 + \beta_3 x^3 + \varepsilon\) (kubische Regression = Polynomregression 3. Grades)
Alle dieser Modelle sind “lineare Modelle”, da sie linear in ihren Parametern β sind. Die entscheidende Eigenschaft ist, dass jeder Parameter \(\beta_j\) linear (d.h. mit Potenz 1) in die Gleichung eingeht. Die unabhängigen Variablen (x, x², x³) können durchaus nicht-linear sein, aber die Parameter β tauchen nur als Multiplikatoren auf.
Im Gegensatz dazu wären folgende Modelle nicht linear:
- \(y = \beta_0 + \beta_1^x + \varepsilon\)
- \(y = \beta_0 + x^{\beta_1} + \varepsilon\)
- \(y = \beta_0 + \frac{1}{\beta_1 + x} + \varepsilon\)
Diese Linearität in den Parametern ist der Grund, warum für lineare Modelle eine geschlossene mathematische Lösung mittels Matrixalgebra existiert (die OLS-Methode; siehe Kapitel zur Regression), während nicht-lineare Modelle iterative Optimierungsverfahren wie beim Maximum-Likelihood-Ansatz erfordern, die rechenintensiver sind und nicht immer zum globalen Optimum konvergieren.
Polynomregression
Die Polynomregression ist eine spezielle Form des linearen Modells, bei der wir Potenzen der unabhängigen Variablen als zusätzliche Prädiktoren verwenden. Das allgemeine Modell für eine Polynomregression vom Grad p sieht so aus:
\[y = \beta_0 + \beta_1 x + \beta_2 x^2 + \beta_3 x^3 + \beta_4 x^4 + \ldots + \beta_p x^p + \varepsilon\]
Wir können dieses Modell also gewissermaßen als eine multiple lineare Regression betrachten, bei der die Prädiktoren \(x, x^2, x^3, x^4, \ldots, x^p\) sind - es sind also eben nicht verschieden Variablen/Spalten, sondern dieselbe, bloß in verschiedenen Potenzen. Fürs Gefühl hier ein Video, bei dem ich bei dem desmos Grafikrechner mit den Koeffizienten spiele und die verschiedenen Polynomgrade veranschauliche:
Es sei übrigens direkt betont, dass für die Bezeichnung wichtig ist was das höchste Polynom ist, nicht wie viele Prädiktoren wir haben. Folgende Modelle können alle gleichermaßen als Polynom 2. Grades bezeichnet werden:
- \(y = \beta_0 + \beta_1 x + \beta_2 x^2 + \varepsilon\)
- \(y = \beta_0 + \beta_2 x^2 + \varepsilon\)
- \(y = \beta_2 x^2 + \varepsilon\)
Boston Housing Dataset
Schauen wir uns das Boston Housing Dataset als Beispiel an. Wir konzentrieren uns auf die Beziehung zwischen den Variablen NOX (Stickoxidkonzentration) und DIS (Entfernung zu Beschäftigungszentren):
# Boston Housing Datensatz laden
pfad = "https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/boston_housing/boston_house_prices.csv"
boston = pd.read_csv(pfad, skiprows=1)
# NOX vs. DIS visualisieren
fig, ax = plt.subplots(figsize=(10, 6))
ax.scatter(boston['DIS'], boston['NOX'], alpha=0.6)
ax.set_xlabel('Gewichtete Entfernung zu Beschäftigungszentren (DIS)')
ax.set_ylabel('Stickoxidkonzentration in ppm (NOX)')
ax.set_title('NOX vs. DIS')
plt.show()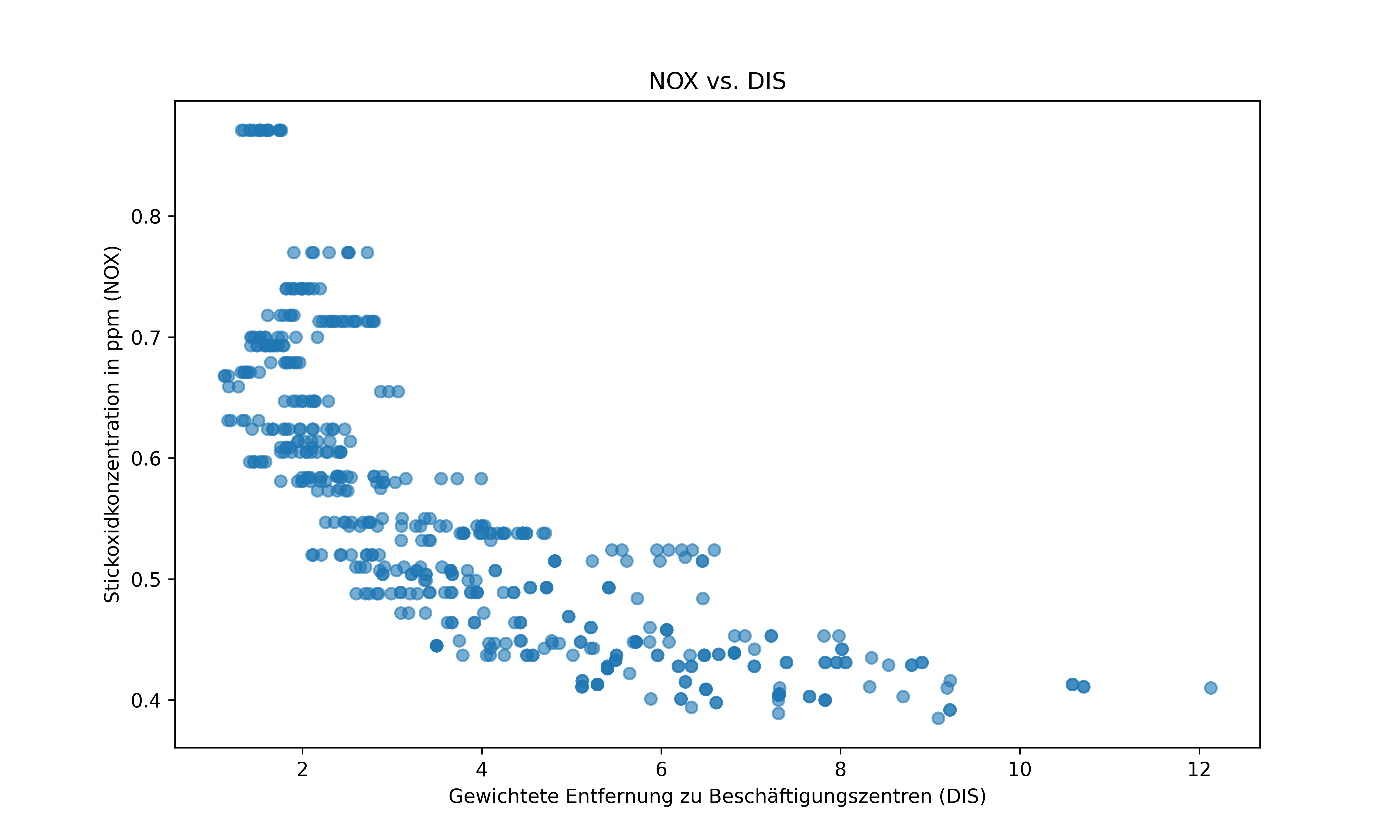
Aus dem Streudiagramm können wir erkennen, dass die Beziehung zwischen NOX und DIS offensichtlich nicht-linear ist. Die Stickoxidkonzentration nimmt mit zunehmender Entfernung zu Beschäftigungszentren stark ab, flacht dann aber ab. Diese Art von Beziehung könnte vermutlich besser durch ein Polynom höheren Grades als durch eine einfache lineare Regression beschrieben werden.
Implementierung der Polynomregression
Wir werden verschiedene Polynomgrade für die Beziehung zwischen NOX und DIS testen, um zu sehen, welcher am besten passt.
scikit-learn
Bei scikit-learn müssen wir polynomiale Features explizit erstellen:
# Daten vorbereiten
X = boston['DIS'].values.reshape(-1, 1) # Unabhängige Variable als 2D-Array
y = boston['NOX'].values # Abhängige Variable
# Polynomiale Features verschiedener Grade erstellen
X_poly_1 = PolynomialFeatures(degree=1, include_bias=False).fit_transform(X)
X_poly_2 = PolynomialFeatures(degree=2, include_bias=False).fit_transform(X)
X_poly_3 = PolynomialFeatures(degree=3, include_bias=False).fit_transform(X)
X_poly_4 = PolynomialFeatures(degree=4, include_bias=False).fit_transform(X)
# Modelle verschiedener Grade mit scikit-learn anpassen
mod_1_sklearn = LinearRegression().fit(X_poly_1, y)
mod_2_sklearn = LinearRegression().fit(X_poly_2, y)
mod_3_sklearn = LinearRegression().fit(X_poly_3, y)
mod_4_sklearn = LinearRegression().fit(X_poly_4, y)
# Hinweis: Die Vorhersage und Koeffizientenextraktion erfolgt wie in den vorherigen Kapiteln
# beschrieben und liefert die gleichen Ergebnisse wie die statsmodels-Implementierung untenUm zu verstehen wie genau wir oben die polynomialen Features erstellt haben, wenden wir die Funktion am besten auf ein einfaches Beispiel an, nämlich nur auf die Werte 2 und 3 für ein Polynom 3. Grades:
PolynomialFeatures(degree=3, include_bias=False).fit_transform([[2], [3]])array([[ 2., 4., 8.],
[ 3., 9., 27.]])Wie man sieht wird hier für jeden der beiden Werte die Potenz 1, 2 und 3 erstellt, also [x, x², x³]. Genau dasselbe führen wir also für unsere DIS Werte durch - hier mal für die ersten 5 gezeigt
X = boston['DIS'].values.reshape(-1, 1)
PolynomialFeatures(degree=3, include_bias=False).fit_transform(X[:5])array([[ 4.09 , 16.7281 , 68.417929 ],
[ 4.9671 , 24.67208241, 122.54870054],
[ 4.9671 , 24.67208241, 122.54870054],
[ 6.0622 , 36.75026884, 222.78747976],
[ 6.0622 , 36.75026884, 222.78747976]])Wir erzeugen uns also sozusagen einen neuen Datensatz, der tatsächlich nicht nur die Spalte DIS, sondern auch die Spalten DIS² und DIS³ enthält. Mit anderen Worten: Wir führen vorm Modellieren eine Transformation der Daten durch, um die polynomialen Features zu erstellen und übergeben diese dann dem Modell.
Das Argument include_bias=False sorgt dafür, dass der Bias (der Intercept) nicht mitberechnet wird. Wenn wir include_bias=True setzen, wird auch eine Spalte mit Einsen1 für den Bias hinzugefügt:
PolynomialFeatures(degree=3, include_bias=True).fit_transform([[2], [3]])array([[ 1., 2., 4., 8.],
[ 1., 3., 9., 27.]])Wir brauchen das nicht, da wir den Intercept in der Regression ohnehin mitberechnen, da in der Funktion LinearRegression() wiederum fit_intercept=True standardmäßig gesetzt ist. Wir verhinden also, dass wir den Intercept doppelt berechnen.
Schließlich sei noch vorweggenommen, dass PolynomialFeatures() auch die Interaktionstermine zwischen den Variablen berechnen kann, wenn wir mehrere unabhängige Variablen haben. Das ist hier nicht der Fall, da wir nur eine unabhängige Variable (DIS) haben. Hätten wir aber neben \(x_1\) noch eine zweite unabhängige Variable \(x_2\), würden wir direkt auch die entsprechenden Interaktionsterme erhalten, was uns in Richtung der Response Surface Methodology (RSM) führt. So erhalten wir also hier beispielsweise [x₁, x₂, x₁², x₁x₂, x₂²]:
PolynomialFeatures(degree=2, include_bias=False).fit_transform([[2, 3], [4, 5]])array([[ 2., 3., 4., 6., 9.],
[ 4., 5., 16., 20., 25.]])statsmodels
Anders als bei scikit-learn, wo wir die polynomialen Terme durch eine separate Transformation (PolynomialFeatures) vorbereiten müssen, können wir bei statsmodels alle Potenzen direkt via Formelnotation definieren - allerdings müssen wir explizit angeben, dass es sich um ein mathematische Operation auf eine Variable handelt, indem wir I() verwenden.
# Modelle verschiedener Grade mit statsmodels
mod_1_sm = smf.ols(formula='NOX ~ DIS', data=boston).fit()
mod_2_sm = smf.ols(formula='NOX ~ DIS + I(DIS**2)', data=boston).fit()
mod_3_sm = smf.ols(formula='NOX ~ DIS + I(DIS**2) + I(DIS**3)', data=boston).fit()
mod_4_sm = smf.ols(formula='NOX ~ DIS + I(DIS**2) + I(DIS**3) + I(DIS**4)', data=boston).fit()Für einen einfachen Vergleich der Modelle können wir die Koeffizienten in einem DataFrame zusammenfassen:
# DataFrame mit Koeffizienten erstellen
coef_df = pd.DataFrame(
columns=['Intercept', 'DIS', 'DIS²', 'DIS³', 'DIS⁴'],
index=['Grad 1', 'Grad 2', 'Grad 3', 'Grad 4']
)
# Parameter für jedes Modell extrahieren
models = {
'Grad 1': mod_1_sm,
'Grad 2': mod_2_sm,
'Grad 3': mod_3_sm,
'Grad 4': mod_4_sm
}
for grad, model in models.items():
for param in model.params.index:
coef_df.loc[grad, param.replace('I(DIS ** 2)', 'DIS²')
.replace('I(DIS ** 3)', 'DIS³')
.replace('I(DIS ** 4)', 'DIS⁴')] = model.params[param]
print(coef_df) Intercept DIS DIS² DIS³ DIS⁴
Grad 1 0.715343 -0.042331 NaN NaN NaN
Grad 2 0.843991 -0.111628 0.007135 NaN NaN
Grad 3 0.934128 -0.182082 0.021928 -0.000885 NaN
Grad 4 0.952222 -0.200804 0.02805 -0.001656 0.000032Nun lassen wir uns von jedem Modell Vorhersagen für die verschiedenen DIS-Werte machen…
# Vorhersagen für eine glatte Linie
X_pred = np.linspace(boston['DIS'].min(), boston['DIS'].max(), 100)
pred_df = pd.DataFrame({'DIS': X_pred})
y_pred_1 = mod_1_sm.predict(pred_df)
y_pred_2 = mod_2_sm.predict(pred_df)
y_pred_3 = mod_3_sm.predict(pred_df)
y_pred_4 = mod_4_sm.predict(pred_df)… und visualisieren die Ergebnisse schließlich in einem Diagramm:
# Visualisierung
fig, ax = plt.subplots(figsize=(10, 6))
# Datenpunkte
ax.scatter(boston['DIS'], boston['NOX'], alpha=0.6, label='Beobachtungen')
# Regressionskurven für verschiedene Grade mit Formeln in der Legende
ax.plot(X_pred, y_pred_1, color='red',
label=f"Grad 1: NOX = {coef_df.loc['Grad 1', 'Intercept']:.3f} + {coef_df.loc['Grad 1', 'DIS']:.3f}·DIS")
ax.plot(X_pred, y_pred_2, color='green',
label=f"Grad 2: NOX = {coef_df.loc['Grad 2', 'Intercept']:.3f} + {coef_df.loc['Grad 2', 'DIS']:.3f}·DIS + {coef_df.loc['Grad 2', 'DIS²']:.3f}·DIS²")
ax.plot(X_pred, y_pred_3, color='blue',
label=f"Grad 3: NOX = {coef_df.loc['Grad 3', 'Intercept']:.3f} + ... + {coef_df.loc['Grad 3', 'DIS³']:.3f}·DIS³")
ax.plot(X_pred, y_pred_4, color='purple',
label=f"Grad 4: NOX = {coef_df.loc['Grad 4', 'Intercept']:.3f} + ... + {coef_df.loc['Grad 4', 'DIS⁴']:.3f}·DIS⁴")
ax.set_xlabel('Gewichtete Entfernung zu Beschäftigungszentren (DIS)')
ax.set_ylabel('Stickoxidkonzentration in ppm (NOX)')
ax.set_title('NOX vs. DIS: Vergleich verschiedener Polynomgrade')
ax.legend(loc='upper right', fontsize=8)
plt.show()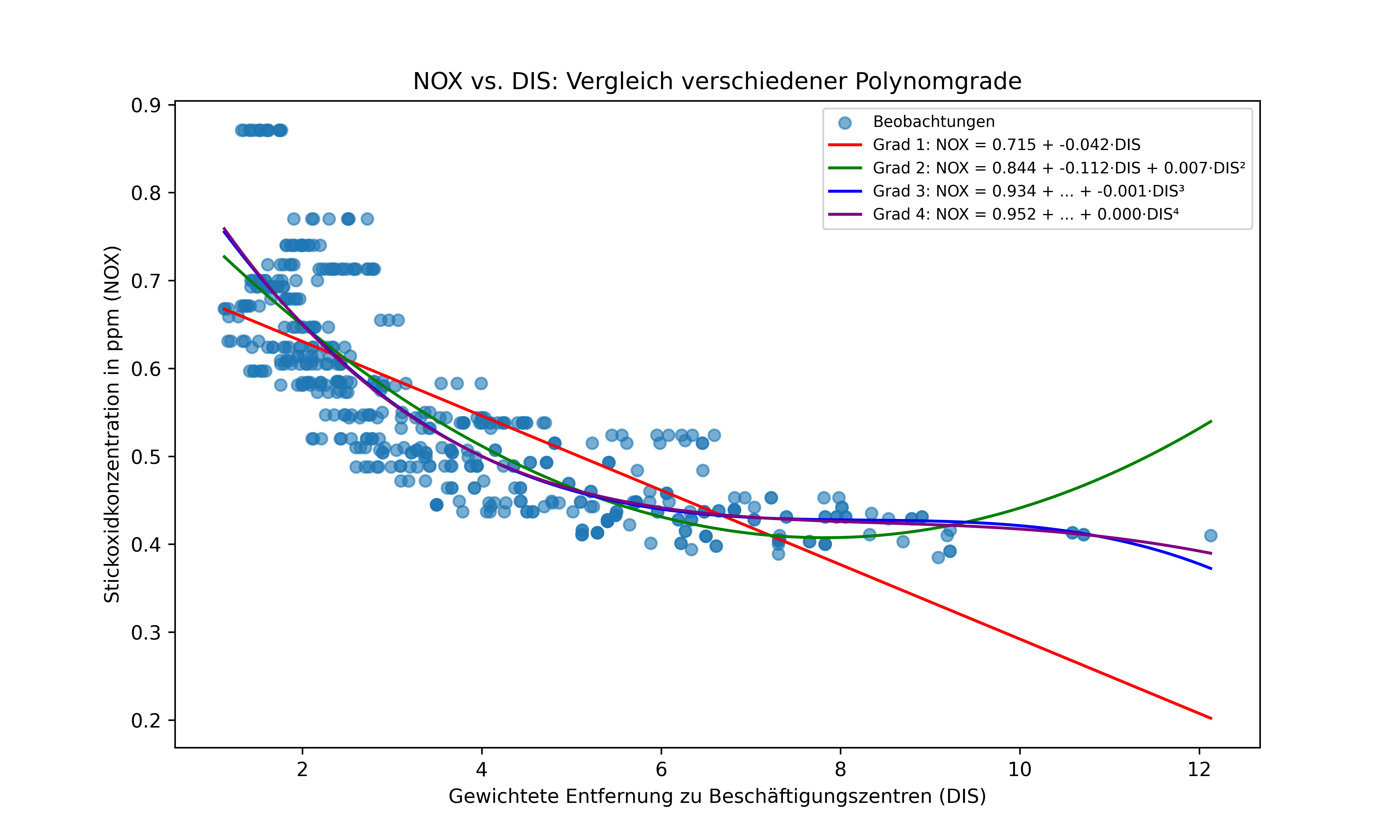
Wahl des optimalen Modells
Bei Betrachtung der Abbildung fällt auf, dass das lineare Modell (Grad 1) die Krümmung in den Daten nicht gut erfasst. Die Modelle höheren Grades scheinen besser zu passen, aber welches ist nun objektiv das beste? Um diese Frage zu beantworten, können wir verschiedene Informationskriterien heranziehen.
Modellvergleich mit Informationskriterien
Wir vergleichen die Modelle anhand verschiedener Kriterien: das R², das adjustierte R², das Akaike Information Criterion (AIC) und das Bayesian Information Criterion (BIC):
models = [mod_1_sm, mod_2_sm, mod_3_sm, mod_4_sm]
mod_comparison = pd.DataFrame({
'Polynomgrad': range(1, 5),
'R²': [m.rsquared for m in models],
'Adj. R²': [m.rsquared_adj for m in models],
'AIC': [m.aic for m in models],
'BIC': [m.bic for m in models]
})
print(mod_comparison)
# Bestes Modell nach jedem Kriterium
best_r2 = mod_comparison.loc[mod_comparison['R²'].idxmax()]
best_adj_r2 = mod_comparison.loc[mod_comparison['Adj. R²'].idxmax()]
best_aic = mod_comparison.loc[mod_comparison['AIC'].idxmin()]
best_bic = mod_comparison.loc[mod_comparison['BIC'].idxmin()]
print(f"\nBestes Modell nach R²: Grad {int(best_r2['Polynomgrad'])}")
print(f"Bestes Modell nach Adj. R²: Grad {int(best_adj_r2['Polynomgrad'])}")
print(f"Bestes Modell nach AIC: Grad {int(best_aic['Polynomgrad'])}")
print(f"Bestes Modell nach BIC: Grad {int(best_bic['Polynomgrad'])}") Polynomgrad R² Adj. R² AIC BIC
0 1 0.591715 0.590905 -1195.387608 -1186.934535
1 2 0.699856 0.698663 -1349.085766 -1336.406156
2 3 0.714774 0.713069 -1372.881101 -1355.974954
3 4 0.714940 0.712664 -1371.175608 -1350.042924
Bestes Modell nach R²: Grad 4
Bestes Modell nach Adj. R²: Grad 3
Bestes Modell nach AIC: Grad 3
Bestes Modell nach BIC: Grad 3Visualisierung der Informationskriterien
Speziell für diesen Fall, wo wir Modelle miteinander vergleichen, die jeweils im Polynomgrad um 1 höher sind, können wir gut ein Diagramm erstellen, das die verschiedenen Informationskriterien für die verschiedenen Polynomgrade zeigt:
# Visualisierung der Kriterien in 2x2 Anordnung
fig, axs = plt.subplots(2, 2, figsize=(14, 10), layout='tight')
axs = axs.flatten()
# R²
axs[0].plot(mod_comparison['Polynomgrad'], mod_comparison['R²'], marker='o', color='orange')
axs[0].set_xlabel('Polynomgrad')
axs[0].set_ylabel('R²')
axs[0].set_title('R² vs. Polynomgrad')
axs[0].axvline(x=mod_comparison.loc[mod_comparison['R²'].idxmax(), 'Polynomgrad'], color='red', linestyle='--')
axs[0].grid(True)
# Adjustiertes R²
axs[1].plot(mod_comparison['Polynomgrad'], mod_comparison['Adj. R²'], marker='o', color='purple')
axs[1].set_xlabel('Polynomgrad')
axs[1].set_ylabel('Adj. R²')
axs[1].set_title('Adjustiertes R² vs. Polynomgrad')
axs[1].axvline(x=mod_comparison.loc[mod_comparison['Adj. R²'].idxmax(), 'Polynomgrad'], color='red', linestyle='--')
axs[1].grid(True)
# AIC
axs[2].plot(mod_comparison['Polynomgrad'], mod_comparison['AIC'], marker='o', color='blue')
axs[2].set_xlabel('Polynomgrad')
axs[2].set_ylabel('AIC')
axs[2].set_title('AIC vs. Polynomgrad')
axs[2].axvline(x=mod_comparison.loc[mod_comparison['AIC'].idxmin(), 'Polynomgrad'], color='red', linestyle='--')
axs[2].grid(True)
# BIC
axs[3].plot(mod_comparison['Polynomgrad'], mod_comparison['BIC'], marker='o', color='green')
axs[3].set_xlabel('Polynomgrad')
axs[3].set_ylabel('BIC')
axs[3].set_title('BIC vs. Polynomgrad')
axs[3].axvline(x=mod_comparison.loc[mod_comparison['BIC'].idxmin(), 'Polynomgrad'], color='red', linestyle='--')
axs[3].grid(True)
plt.show()
Bei der Beurteilung der Modelle müssen wir beachten:
- Das einfache R² steigt immer, wenn wir mehr Parameter zum Modell hinzufügen, selbst wenn diese keinen echten Erklärungswert haben. Demnach ist es hier nicht geeignet, um zwischen den Modellen zu unterscheiden.
- Das adjustierte R², sowie AIC und BIC berücksichtigen die Anzahl der Parameter und bestrafen überangepasste Modelle.
- AIC neigt dazu, komplexere Modelle zu bevorzugen, da es die Modellkomplexität weniger stark bestraft.
- BIC bestraft die Modellkomplexität stärker und bevorzugt daher einfachere Modelle.
- Das adjustierte R² liegt oft zwischen diesen beiden Extremen.
Das führt uns zum nächsten Punkt:
Overfitting vs. Underfitting
Bei der Polynomregression und generell beim statistischen Modellieren stehen wir immer vor dem Dilemma der richtigen Modellkomplexität. Dieses Dilemma lässt sich als Abwägung zwischen Underfitting und Overfitting verstehen.
Lassen wir ein Beispiel erstellen, das dieses Problem veranschaulicht:
np.random.seed(42)
n_samples = 20
X_demo = np.sort(np.random.uniform(0, 10, n_samples)).reshape(-1, 1)
y_demo = np.sin(X_demo.ravel()) + 0.3 * np.random.randn(n_samples)
# Verschiedene Polynomgrade testen
degrees = [1, 10]
labels = ['Gerade (Underfitting)', 'Polynom 10. Grades (Overfitting)']
X_test = np.linspace(0, 10, 1000).reshape(-1, 1)
fig, axs = plt.subplots(1, 2, figsize=(14, 5), layout='tight')
for i, degree in enumerate(degrees):
label = labels[i]
# Datenpunkte plotten (auf beiden Plots)
axs[i].scatter(X_demo, y_demo, s=50, alpha=0.8, label='Datenpunkte')
# Modell anpassen
poly_features = PolynomialFeatures(degree=degree, include_bias=True)
X_poly = poly_features.fit_transform(X_demo)
poly_model = LinearRegression().fit(X_poly, y_demo)
# Vorhersagen
X_test_poly = poly_features.transform(X_test)
y_pred = poly_model.predict(X_test_poly)
# Plotten
axs[i].plot(X_test, y_pred, label=label, color='orange', lw=2)
axs[i].set_xlabel('X')
axs[i].set_ylabel('y')
axs[i].set_title(label)
axs[i].legend()
plt.show()
Die beiden Diagramme stellen die zwei Extreme der Modellkomplexität dar:
Underfitting (zu einfaches Modell):
Das lineare Modell (Grad 1) im linken Diagramm ist zu einfach, um das Muster in den Daten zu erfassen. Es kann den nicht-linearen Zusammenhang nicht abbilden und “unterschätzt” die Komplexität der Daten. Dieses Modell wird sowohl bei den vorhandenen Datenpunkten als auch bei weiteren Daten schlechte Vorhersagen liefern.
Overfitting (zu komplexes Modell):
Das Modell mit Polynomgrad 10 im rechten Diagramm passt sich fast perfekt an jeden einzelnen Datenpunkt an. Es “lernt” dabei nicht nur das zugrundeliegende Muster, sondern auch das zufällige Rauschen in den Daten. Das Modell zeigt extreme Ausschläge zwischen den Datenpunkten und würde bei neuen, bisher ungesehenen Daten wahrscheinlich sehr schlechte Vorhersagen liefern.
Das optimale Modell liegt in der Regel irgendwo zwischen diesen beiden Extremen – komplex genug, um das tatsächliche Muster in den Daten zu erfassen, aber nicht so komplex, dass es auch das Rauschen modelliert. Finden des optimalen Modells
In diesem Kapitel haben wir gesehen, wie Informationskriterien wie AIC, BIC und das adjustierte R² dabei helfen können, die optimale Modellkomplexität zu finden. Diese Kriterien berücksichtigen sowohl die Anpassungsgüte als auch die Modellkomplexität. Eine weitere wichtige Methode zur Modellselektion ist die Verwendung von Trainings- und Testdaten (Train-Test-Split), bei der ein Teil der Daten zum Trainieren des Modells verwendet wird und der andere Teil zum Testen der Vorhersagegenauigkeit. Diese Methode werden wir in einem späteren Kapitel ausführlicher behandeln. Man kann sich aber schon jetzt vorstellen, dass ein Modell, das für einen bestimmten Datensatz overfitted ist, bei neuen, etwas anderen Daten schlechter abschneiden wird.
Zusammenfassung
In diesem Kapitel haben wir die Polynomregression als Erweiterung der linearen Regression kennengelernt, die es uns ermöglicht, (mit weiterhin linearen Modellen) nicht-lineare Beziehungen zwischen Variablen zu modellieren. Wir haben:
Das mathematische Modell der Polynomregression kennengelernt: \(y = \beta_0 + \beta_1 x + \beta_2 x^2 + \beta_3 x^3 + \ldots + \beta_p x^p + \varepsilon\)
Die Polynomregression in Python mit scikit-learn und statsmodels implementiert
Verschiedene Polynomgrade verglichen
Die Konzepte von Overfitting und Underfitting verstanden und wie sie mit der Modellkomplexität zusammenhängen
Verschiedene Kriterien zur Modellauswahl (AIC, BIC, adjustiertes R²) verglichen
Übungen
Übung 1
Implementiere eine Funktion optimal_polynomial_degree, die den optimalen Polynomgrad für die Beziehung zwischen zwei Variablen anhand verschiedener Informationskriterien bestimmt.
Die Funktion soll folgende Parameter haben:
-
data: Ein DataFrame, der die Daten enthält -
x_name: Name der unabhängigen Variable im DataFrame -
y_name: Name der abhängigen Variable im DataFrame -
max_degree: Maximaler zu prüfender Polynomgrad (Standard: 10) -
criterion: Bevorzugtes Informationskriterium zur Modellauswahl (Standard: ‘aic’, Alternativen: ‘bic’, ‘r2_adj’)
Die Funktion soll:
- Polynomregressionen für alle Grade von 1 bis
max_degreeberechnen - Einen DataFrame zurückgeben mit folgenden Spalten:
-
Polynomgrad: Grad des Polynoms -
AIC,BIC,Adj_R2: Werte der jeweiligen Informationskriterien -
Rang_AIC,Rang_BIC,Rang_Adj_R2: Rangplatzierung der Modelle nach dem jeweiligen Kriterium (Rang 1 = bestes Modell)
-
- Ein Diagramm mit zwei Subplots erstellen:
- Links: Scatterplot der Originaldaten mit der Vorhersagekurve des optimalen Modells (basierend auf dem gewählten Kriterium)
- Rechts: Verlauf aller drei Informationskriterien (auf Werte zwischen 0 und 1 skaliert) in Abhängigkeit vom Polynomgrad, mit einer vertikalen Linie beim optimalen Grad
Teste deine Funktion am Beispiel des Zusammenhangs zwischen MEDV (Immobilienwert) und AGE (Gebäudealter) im Boston Housing Datensatz.
# Beispielaufruf:
pfad = "https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/boston_housing/boston_house_prices.csv"
boston = pd.read_csv(pfad, skiprows=1)
results = optimal_polynomial_degree(boston, 'AGE', 'MEDV', max_degree=10, criterion='aic')
print(results)Fußnoten
Entspricht \(x^0\), also der Potenz 0.↩︎