import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.stats.weightstats import ttest_ind
np.random.seed(42) # für reproduzierbare Ergebnisset-Tests: Mittelwertvergleiche
In den vorangegangenen Kapiteln haben wir uns mit Korrelation und verschiedenen Regression beschäftigt - Methoden, bei denen wir den Zusammenhang zwischen numerischen Variablen untersuchen. Nun machen wir einen wichtigen Schritt: Wir betrachten Situationen, in denen wir Gruppen vergleichen möchten, die durch kategorielle Variablen definiert sind.
Eine der grundlegendsten Fragen in der Datenanalyse lautet: “Unterscheiden sich die Mittelwerte zweier Gruppen voneinander?” Zum Beispiel könnten wir fragen:
- Führt ein neues Medikament zu einer Verbesserung der Symptome im Vergleich zu einem Placebo?
- Erzielen Studierende mit einer neuen Lehrmethode bessere Testergebnisse als mit der herkömmlichen Methode?
- Ist das durchschnittliche Körpergewicht zweier Pinguinarten unterschiedlich?
Der t-Test ist eines der am häufigsten verwendeten statistischen Verfahren, um solche Fragen zu beantworten. In diesem Kapitel werden wir uns mit verschiedenen Arten von t-Tests beschäftigen und lernen, wie sie in Python implementiert werden.
Wie wir bereits im Kapitel über p-Werte und statistische Signifikanz behandelt haben, folgt ein Hypothesentest typischerweise diesen Schritten und wird das somit auch für die folgenden t-tests tun:
- Aufstellen einer Nullhypothese (H₀): “Es gibt keinen Unterschied/Effekt”
- Definition einer Alternativhypothese (H₁): “Es existiert ein Unterschied/Effekt”
- Erhebung von Daten und Berechnung einer Teststatistik
- Ermittlung des p-Werts: Die Wahrscheinlichkeit, unter H₀ eine mindestens so extreme Teststatistik zu beobachten
- Vergleich mit dem Signifikanzniveau (meist \(\alpha\) = 0,05)
- Entscheidung: Bei p < \(\alpha\) verwerfen wir H₀ zugunsten von H₁
Beim t-Test ist die verwendete Teststatistik die t-Statistik, die der t-Verteilung folgt, welche wir bereits im Kapitel über Konfidenzintervalle kennengelernt haben.
Der Palmer Penguins Datensatz
Für die verschiedenen t-Tests in diesem Kapitel verwenden wir den bekannten “Palmer Penguins” Datensatz, der Messungen von drei verschiedenen Pinguinarten auf den Palmer-Inseln in der Antarktis enthält.
Da wir in diesem Kapitel mehrere Versionen derselben Abbildung brauchen erzeugen wir uns außerdem zunächst eine Funktion plot_species (siehe eingeklappter Code) und wenden diese direkt an.

# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}Code zeigen/verstecken
def plot_species(df, species_list, ref_value=None):
"""
Erstellt einen Jitter-Plot des Körpergewichts (body_mass_g) für eine oder mehrere Pinguinarten.
Für jede Art werden:
- alle Einzelbeobachtungen als Punkte (mit Jitter) dargestellt,
- der Mittelwert als horizontale Linie angezeigt,
- optional ein Referenzwert (z.B. für einen Ein-Stichproben-t-Test) hinzugefügt.
Parameter:
-----------
df : pandas.DataFrame
Ein DataFrame mit mindestens den Spalten 'species' und 'body_mass_g'.
species_list : list of str
Liste der zu plottenden Pinguinarten (z.B. ['Adelie', 'Gentoo']).
ref_value : float or None, optional
Optionaler Referenzwert, der als horizontale Linie dargestellt wird
(z.B. 4000 für einen Ein-Stichproben-t-Test). Wird nur gezeigt,
wenn genau eine Spezies dargestellt wird.
Rückgabewert:
-------------
Es wird ein matplotlib-Plot angezeigt. Die Funktion gibt selbst nichts zurück.
"""
# Plot-Setup
fig, ax = plt.subplots(figsize=(7, 4), layout='tight')
# Filtere nur relevante Arten und entferne NA-Werte in 'body_mass_g'
df_plot = df[df['species'].isin(species_list)].dropna(subset=['body_mass_g'])
# x-Positionen auf der Achse für jede Art
x_positions = {sp: i for i, sp in enumerate(species_list)}
# Durchlaufe alle gewünschten Arten
for species in species_list:
# Wähle Daten für die aktuelle Art
data = df_plot[df_plot['species'] == species]['body_mass_g']
# Erzeuge leicht gestreute x-Werte (Jitter), damit sich Punkte nicht überlappen
x_jitter = np.random.normal(loc=x_positions[species], scale=0.05, size=len(data))
# Streudiagramm der Einzelbeobachtungen
ax.scatter(x_jitter, data, alpha=0.7, s=20, color=colors[species])
# Berechne und plotte den Mittelwert als gestrichelte Linie
mean_val = data.mean()
ax.hlines(y=mean_val, xmin=x_positions[species]-0.2, xmax=x_positions[species]+0.2,
colors="black", linestyles='--', linewidth=2)
# Textbeschriftung für den Mittelwert
ax.text(x_positions[species]+0.25, mean_val, f"{mean_val:.0f} g",
va='center', ha='left', fontsize=9, color=colors[species])
# Optional: Referenzwert für Ein-Stichproben-Test (nur bei einer Art)
if ref_value is not None and len(species_list) == 1:
ax.hlines(y=ref_value, xmin=-0.2, xmax=0.2, colors='red', linestyles='-', linewidth=2)
ax.text(0.25, ref_value, f"{ref_value} g (Referenzwert)", va='center', ha='left',
fontsize=9, color='red')
# Achsenbeschriftungen und kosmetische Einstellungen
ax.set_ylabel('Körpergewicht (g)')
ax.set_xticks(list(x_positions.values()))
ax.set_xticklabels(species_list)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
# Plot anzeigen
plt.show()Die Art des Plots, den wir hier verwenden, wird als Jitter-Plot bezeichnet. Dabei handelt es sich um ein Streudiagramm/Scatterplot, bei dem die Punkte leicht zufällig verschoben werden (Jitter), um Überlappungen zu vermeiden und die Verteilung der Daten besser sichtbar zu machen. Dies ist besonders nützlich, wenn viele Datenpunkte denselben Wert haben. Zufällig verschoben werden sie in diesem Fall natürlich nur nach links und rechts, also entlang der x-Achse und dann auch nur so viel, dass noch immer klar ist zu welcher Art der Punkt gehört. Auf der y-Achse bleibt der Wert unverändert, da man ja sonst die Daten verfälschen würde.
Mehr zu dieser und verwandten Darstellungen gibt’s in einem folgenden DV-Kapitel.
plot_species(penguins, ['Adelie', 'Chinstrap', 'Gentoo'])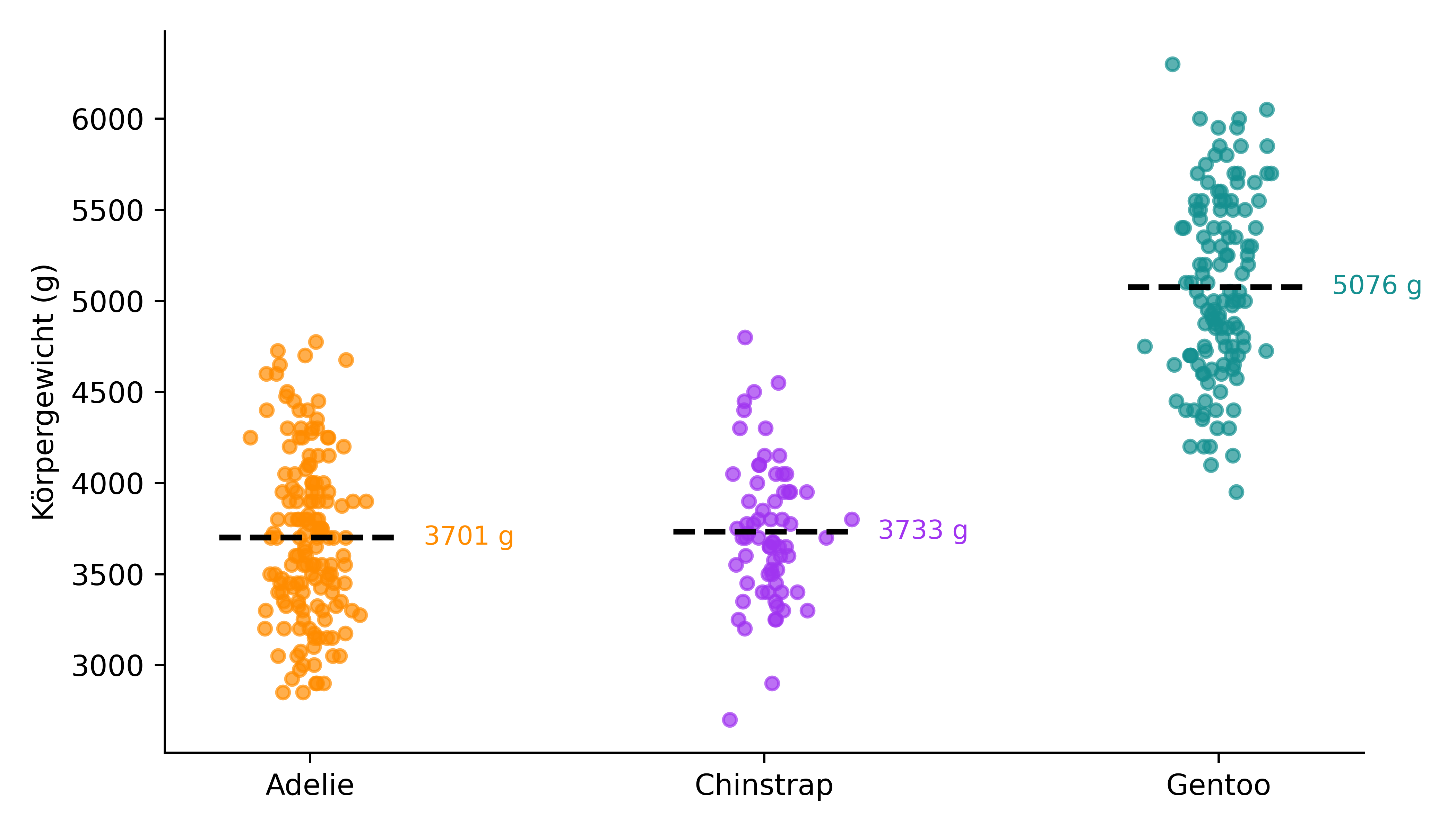
Die Abbildung zeigt also die Körpergewichte der drei Pinguinarten. Wir sehen, dass die Adelie- und Chinstrap-Pinguine im Schnitt etwa ähnlich schwer sind, während die Gentoo-Pinguine deutlich schwerer sind.
Die t-Test-Familie
Es gibt verschiedene Arten von t-Tests, die je nach Fragestellung und Datenstruktur eingesetzt werden:
-
Ein-Stichproben-t-Test (Einzelstichproben-t-Test, One-sample t-test, Single-sample t-test):
Vergleich eines Mittelwerts einer Stichprobe mit einem Referenzwert - Gepaarter t-Test (Abhängiger t-Test, Verbundener t-Test, Paarvergleichstest, Paired t-test, Paired-samples t-test, Dependent t-test, Matched-pairs t-test, Within-subjects t-test): Vergleich der Mittelwerte von zwei abhängigen Gruppen
-
Unabhängiger t-Test (Zweistichproben-t-Test, Unverbundener t-Test, Independent t-test, Two-sample t-test, Between-subjects t-test, Unpaired t-test): Vergleich der Mittelwerte von zwei unabhängigen Gruppen
-
Student’s t-Test (t-Test nach Student, Zweistichproben-t-Test mit gleichen Varianzen, Equal-variance t-test, Pooled-variance t-test):
Setzt gleiche Varianzen der beiden Stichproben voraus -
Welch-Test (Welch-t-Test, Satterthwaite-Test, Smith-Satterthwaite-Test, Unequal-variance t-test, Separate-variance t-test, Welch’s t-test):
Berücksichtigt unterschiedliche Varianzen der beiden Stichproben (robuster)
-
Student’s t-Test (t-Test nach Student, Zweistichproben-t-Test mit gleichen Varianzen, Equal-variance t-test, Pooled-variance t-test):
Die Wahl des richtigen Tests hängt von der Art der Daten und der Fragestellung ab.
Ein-Stichproben-t-Test
Der Ein-Stichproben-t-Test vergleicht den Mittelwert einer einzelnen Stichprobe mit einem vorgegebenen Wert. Die Nullhypothese lautet hier: “Der Mittelwert der Population ist gleich einem bestimmten Wert μ₀.” In der Praxis kann das ein Referenzwert oder ein theoretischer Wert sein, den wir testen möchten. Ein greifbares Beispiel wäre z.B. die Überprüfung, ob ein Messgerät korrekt kalibriert ist. Angenommen, eine Maschine soll eine bestimmte Länge messen, und wir kennen den exakten Sollwert. Ein Techniker nimmt ein Teil, das 30 mm lang ist und führt nun mehrere Messungen durch. Wenn das Gerät korrekt funktioniert, sollten sich diese Abweichungen im Mittel zu null ausgleichen – das heißt, der erwartete Mittelwert ist 30 mm. Mithilfe eines Ein-Stichproben-t-Tests kann man nun prüfen, ob die mittlere Abweichung in der Stichprobe tatsächlich gleich null ist, oder ob eine systematische Verschiebung vorliegt – also ein Hinweis darauf, dass die Maschine falsch kalibriert ist.
Als Datenbeispiel in diesem Kapitel betrachten wir nur die Adelie-Pinguine und testen, ob ihr durchschnittliches Körpergewicht von einem Beispiel-Referenzwert von 4000 g abweicht. Wir wissen bereits, dass der Mittelwert der Adelie-Pinguin-Stichprobe 3701 g beträgt:
plot_species(penguins, ['Adelie'], ref_value=4000)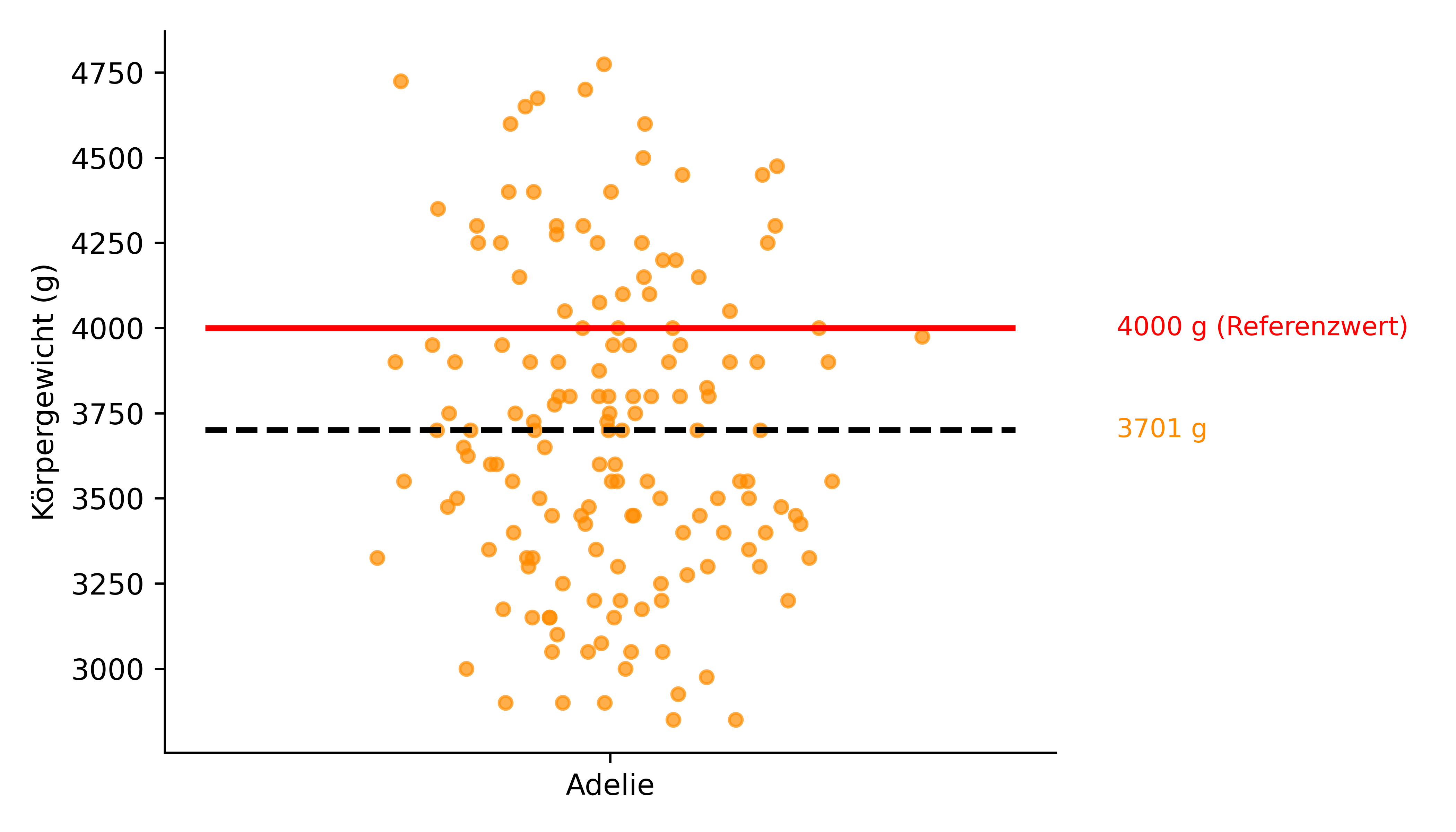
Die Nullhypothese lautet hier: “Das durchschnittliche Körpergewicht der Adelie-Pinguin-Population ist gleich 4000 g.” Wir nehmen also wieder an, dass die Daten normalverteilt sind und legen die entsprechende t-Verteilung um 4000 g zu Grunde. Dann schauen wir, wo auf dieser Verteilung um unseren Referenzwert 4000 g die t-Statistik für unsere Stichprobe liegt. Wenn der Referenzwert in der Nähe des Mittelwerts liegt, ist die Wahrscheinlichkeit, dass wir diesen Wert beobachten, hoch. Liegt er jedoch weit entfernt, ist die Wahrscheinlichkeit gering und wir können die Nullhypothese ablehnen.
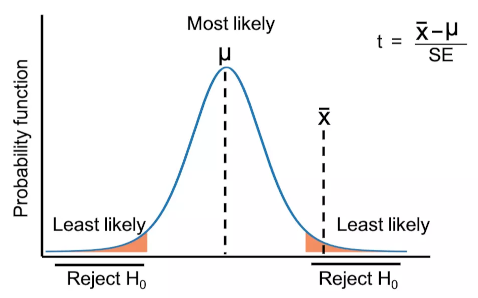
Quelle: Renesh Bedre
Die t-Statistik für einen Ein-Stichproben-t-Test wird wie folgt berechnet:
\[t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}}\]
wobei \(\bar{x}\) der Stichprobenmittelwert (=3701), \(\mu_0\) der Testwert (=4000), \(s\) die Stichprobenstandardabweichung und \(n\) die Stichprobengröße ist. Wir haben also ein Verhältnis von dem Unterschied zwischen dem Stichprobenmittelwert und dem Testwert (Zähler) und dem Standardfehler des Mittelwerts (Nenner).
Man könnte sich jetzt wundern warum in der Formel für die t-Statistik nur die Stichprobengröße \(n\) , nicht jedoch der Term \(n−1\) für die Freiheitsgrade erscheint. Tatsächlich sind die Freiheitsgrade aber letztendlich doch an zwei Stellen relevant: Erstens wurde bei der Berechnung der Stichprobenstandardabweichung \(s\) bereits der Nenner \(n-1\) verwendet, um für die Schätzung eines Parameters zu korrigieren. Zweitens werden die Freiheitsgrade \((df=n−1)\) im nächsten Schritt benötigt, um die entsprechende t-Verteilung auszuwählen, mit der die berechnete t-Statistik verglichen wird, um den p-Wert zu ermitteln. Somit fließen die Freiheitsgrade also doch in die gesamte Testprozedur ein.
Um einen entsprechenden Ein-Stichproben-t-Test durchzuführen, nutzen wir scipy.stats.ttest_1samp():
adelie = penguins[penguins['species'] == 'Adelie']['body_mass_g'].dropna()
t_stat, p_value = stats.ttest_1samp(adelie, 4000)
print(f"Mittleres Körpergewicht der Adelie-Pinguine: {adelie.mean():.2f} g")
print(f"Standardabweichung: {adelie.std(ddof=1):.2f} g")
print(f"Referenzwert: 4000 g")
print(f"t-Statistik: {t_stat:.4f}")
if p_value < 0.05:
print(f"Der Unterschied ist statistisch signifikant (p = {p_value:.20f} < 0.05)")
else:
print(f"Der Unterschied ist nicht statistisch signifikant (p = {p_value:.4f} ≥ 0.05)")Mittleres Körpergewicht der Adelie-Pinguine: 3700.66 g
Standardabweichung: 458.57 g
Referenzwert: 4000 g
t-Statistik: -8.0214
Der Unterschied ist statistisch signifikant (p = 0.00000000000027657736 < 0.05)In diesem Fall lehnen wir also die Nullhypothese ab, da der p-Wert kleiner als 0,05 ist. Das bedeutet, dass das durchschnittliche Körpergewicht der Adelie-Pinguine signifikant von 4000 g abweicht, wir also nicht länger davon ausgehen, dass der wahre Populationsmittelwert 4000 g beträgt.
Der eben verwendete Test war übrigens ein zweiseitiger t-Test. Das bedeutet, dass wir prüfen, ob der Mittelwert signifikant von 4000 g abweicht – egal in welche Richtung also ob er größer oder kleiner 4000 g ist.
Manchmal hat man aber eine klare Idee davon in welche Richtung man solch eine Abweichung prüfen möchte. Beispielsweise könnten wir vermuten, dass die Adelie-Pinguine leichter sind als 4000 g. Das heißt, wir interessieren uns nur für eine Richtung des Unterschieds. So können wir auch einen einseitigen t-test durchführen. Dann ändern sich die Hypothesen also wie folgt:
- H₀: Der Mittelwert ist größer oder gleich 4000g (vorher bei zweiseitig war es nur “gleich”)
- H₁: Der Mittelwert ist kleiner als 4000g (vorher bei zweiseitig war es “nicht gleich”)
Der Fakt, dass der Unterschied zwischen Mittelwert und Referenzwert nur in eine Richtung getestet wird ist natürlich eine zusätzliche Information gegenüber dem zweiseitigen Test. Als Folge haben wir auch aus statistischer Sicht den Vorteil, dass wir unsere 5% Irrtumswahrscheinlichkeit nur auf eine Seite der Verteilung anwenden. Wir brauchen also nicht mehr 2,5% auf jeder Seite der Verteilung, sondern nur noch 5% auf einer Seite “abschneiden”. Dementsprechend wird das abgeschnittene Ende größer und der kritische Bereich des Tests ist größer. Das bedeutet, dass wir auch bei einem kleineren Unterschied zwischen Mittelwert und Referenzwert als statistisch signifikant erkennen können.
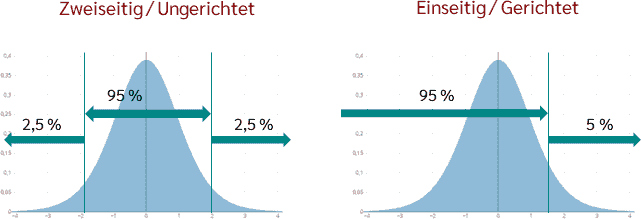
Quelle: Datatab
In Python lässt sich dies durch die Option alternative='less' oder alternative='greater' im ttest_1samp()-Befehl angeben. Standardmäßig ist dies nämlich auf alternative='two-sided' gesetzt.
stats.ttest_1samp(adelie, 4000, alternative='less')Dies gilt nicht nur für den Ein-Stichproben-t-Test, sondern auch für alle folgenden t-Tests! Das heißt, dass wir auch bei den gepaarten und unabhängigen t-Tests die Richtung angeben können und das auch immer mit genau demselben Argument alternative tun.
Gepaarter t-Test
Der gepaarte t-Test wird verwendet, wenn wir zwei abhängige Stichproben haben - zum Beispiel Messungen derselben Subjekte zu zwei verschiedenen Zeitpunkten. Mit anderen Worten: Ein Wert aus der einen Stichprobe gehört immer zu genau einem Wert aus der anderen Stichprobe - wie ein linker und ein rechter Schuh desselben Paars. Dieser t-test testet die Hypothese, dass der Mittelwert aller Differenzen zwischen den gepaarten Messungen gleich 0 ist.
Stellen wir uns ein Beispiel vor, bei dem wir das Gewicht von 10 Pinguinen vor und nach der Brutzeit gemessen haben:
# Gewicht vor der Brutzeit (in g)
gewichte_vor = np.array([4203, 3802, 4107, 3901, 4255, 3855, 4058, 4157, 3956, 4302])
# Gewicht nach der Brutzeit (in g) - typischerweise etwas geringer
gewichte_nach = np.array([4030, 3680, 3970, 3775, 4120, 3740, 3890, 3985, 3780, 4185])Um deutlich zu machen, dass jeweils zwei Werte zusammengehören kann man sie bei der Darstellung mit Linien verbinden. Auf diese Weise bekommt man auch schnell ein Gefühl dafür inwiweit sich die einzelnen Differenzen ähneln:
fig, ax = plt.subplots(figsize=(10, 6))
# Verbindungslinien zwischen den Messungen inklusive Punkten an den Enden
for i in range(len(gewichte_vor)):
ax.plot([1, 2], [gewichte_vor[i], gewichte_nach[i]], '-o', color='grey', alpha=0.5)
# Mittelwerte hervorheben
ax.hlines(y=np.mean(gewichte_vor), xmin=0.8, xmax=1.2,
colors="black", linestyles='--', linewidth=2)
ax.hlines(y=np.mean(gewichte_nach), xmin=1.8, xmax=2.2,
colors="black", linestyles='--', linewidth=2)
# Beschriftung
ax.set_xticks([1, 2])
ax.set_xticklabels(['Vor Brutzeit', 'Nach Brutzeit'])
ax.set_ylabel('Gewicht (g)')
ax.set_title('Gewichtsveränderung während der Brutzeit')
plt.show()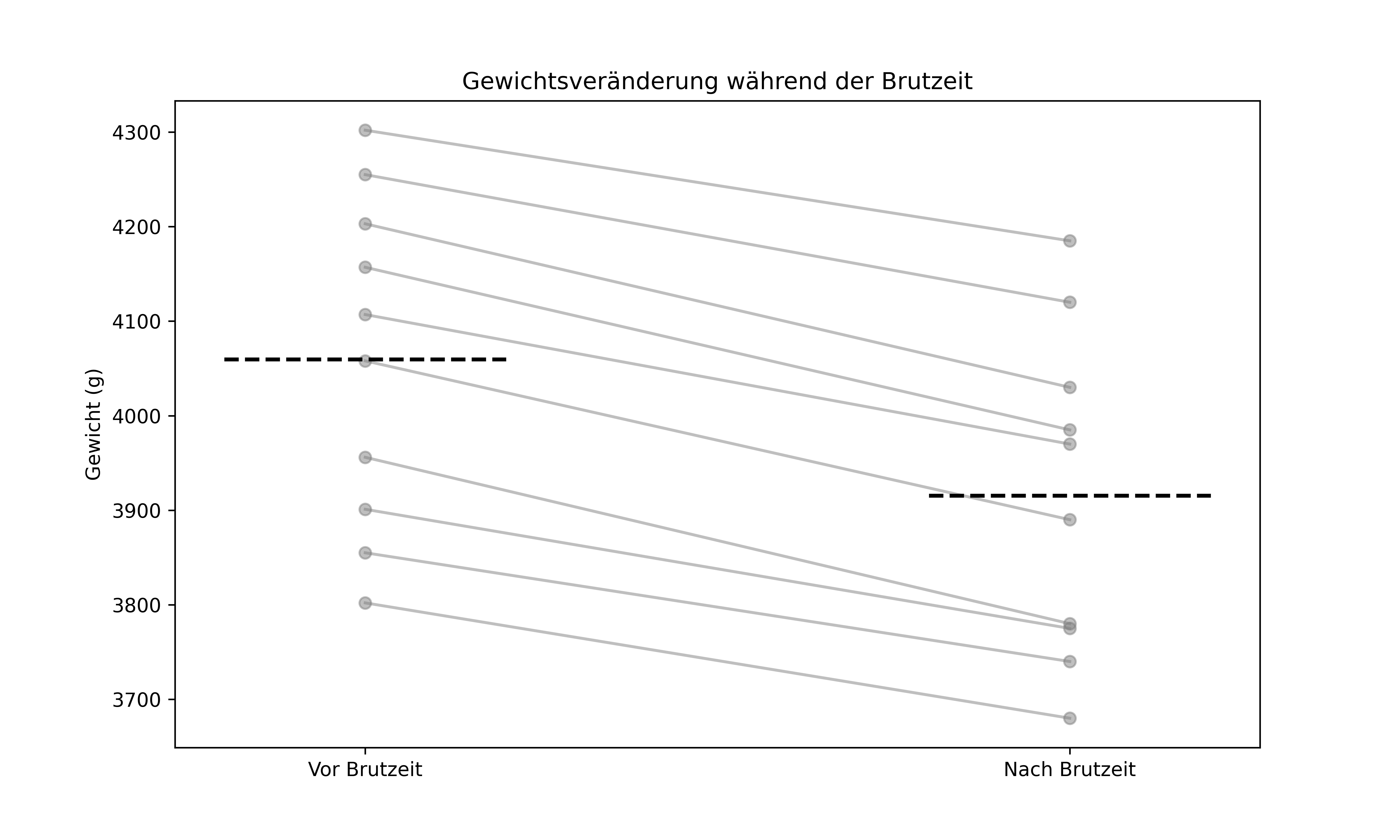
Die t-Statistik für einen gepaarten t-Test ist im Prinzip ein Ein-Stichproben-t-Test auf die Differenzen (mit Referenzwert 0):
\[t = \frac{\bar{d}}{s_d / \sqrt{n}}\]
wobei \(\bar{d}\) der Mittelwert der Differenzen und \(s_d\) die Standardabweichung der Differenzen ist.
# Differenz berechnen
differenzen = gewichte_vor - gewichte_nach
# Gepaarten t-Test durchführen
t_stat, p_value = stats.ttest_rel(gewichte_vor, gewichte_nach)
print(f"Alle Differenzen/Gewichtsabnahmen (in g): {differenzen}")
print(f"Mittlere Differenz/Gewichtsabnahme: {np.mean(differenzen):.2f}g")
print(f"Standardabweichung der Differenz/Gewichtsabnahmen: {np.std(differenzen, ddof=1):.2f}g")
print(f"t-Statistik: {t_stat:.4f}")
if p_value < 0.05:
print(f"Der Unterschied ist statistisch signifikant (p = {p_value:.20f} < 0.05)")
else:
print(f"Der Unterschied ist nicht statistisch signifikant (p = {p_value:.4f} ≥ 0.05)")Alle Differenzen/Gewichtsabnahmen (in g): [173 122 137 126 135 115 168 172 176 117]
Mittlere Differenz/Gewichtsabnahme: 144.10g
Standardabweichung der Differenz/Gewichtsabnahmen: 25.24g
t-Statistik: 18.0550
Der Unterschied ist statistisch signifikant (p = 0.00000002234049142097 < 0.05)Vergleich unabhängiger Gruppen
Nun kommen wir zur vermutlich wichtigsten Anwendung von t-tests: dem Vergleich zweier unabhängiger Gruppen. Hierfür gibt es zwei Varianten des t-Tests:
- Student’s t-Test: Setzt gleiche Varianzen in beiden Gruppen voraus
- Welch-Test: Berücksichtigt unterschiedliche Varianzen (robustere Alternative)
Für diesen Teil wählen wir zwei der drei Pinguinarten aus dem Datensatz und untersuchen, ob sich ihre Körpergewichte unterscheiden:
plot_species(penguins, ['Adelie', 'Gentoo'])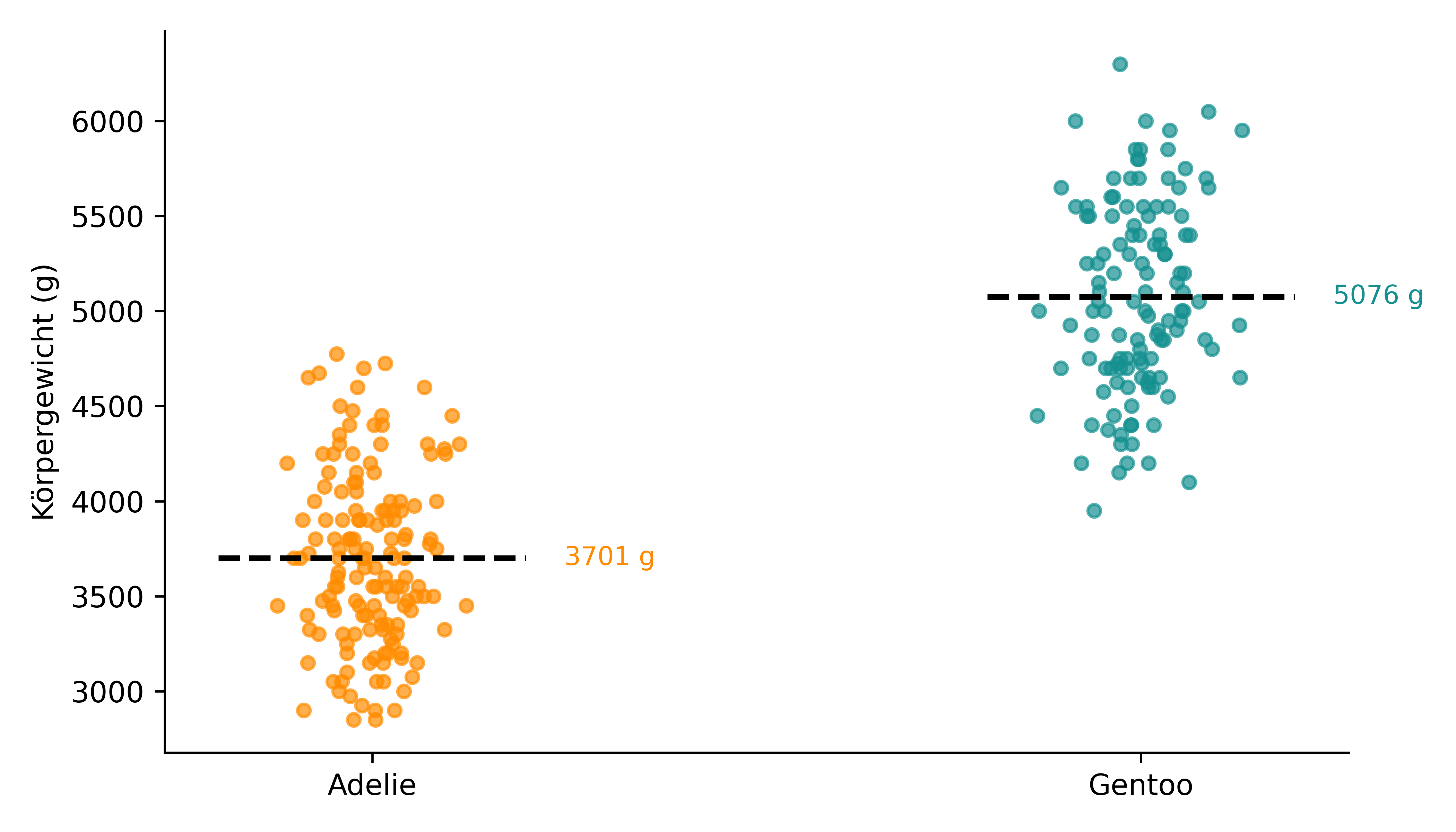
# Untergruppen der zu vergleichenden Arten erstellen
adelie = penguins[penguins['species'] == 'Adelie']['body_mass_g'].dropna()
gentoo = penguins[penguins['species'] == 'Gentoo']['body_mass_g'].dropna()
print(f"Anzahl Adelie Pinguine: {len(adelie)}")
print(f"Anzahl Gentoo Pinguine: {len(gentoo)}")
# Deskriptive Statistiken
print("\nBeschreibende Statistik für Körpergewicht (g):")
print(f"Adelie - Mittelwert: {adelie.mean():.2f}, Standardabweichung: {adelie.std():.2f}")
print(f"Gentoo - Mittelwert: {gentoo.mean():.2f}, Standardabweichung: {gentoo.std():.2f}")
print(f"Differenz der Mittelwerte: {gentoo.mean() - adelie.mean():.2f}")Anzahl Adelie Pinguine: 151
Anzahl Gentoo Pinguine: 123
Beschreibende Statistik für Körpergewicht (g):
Adelie - Mittelwert: 3700.66, Standardabweichung: 458.57
Gentoo - Mittelwert: 5076.02, Standardabweichung: 504.12
Differenz der Mittelwerte: 1375.35Die Frage ist nun also ob der Gewichtsunterschied zwischen Adelie und Gentoo statistisch signifikant ist, oder ob er zufällig entstanden sein könnte.
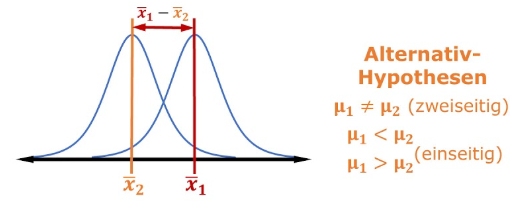
Quelle: Statistik Verstehen
Student’s t-Test (gleiche Varianzen)
Der klassische Student’s t-Test setzt voraus, dass die Varianzen in beiden Gruppen gleich sind. Die Nullhypothese lautet: “Die Mittelwerte beider Populationen sind gleich.”
# Student's t-Test durchführen (equal_var=True)
t_stat, p_value = stats.ttest_ind(adelie, gentoo, equal_var=True)
print("Student's t-Test (gleiche Varianzen):")
print(f"t-Statistik: {t_stat:.4f}")
print(f"p-Wert: {p_value:.60f}")
if p_value < 0.05:
print("Ergebnis: Der Unterschied ist statistisch signifikant (p < 0.05)")
else:
print("Ergebnis: Der Unterschied ist nicht statistisch signifikant (p >= 0.05)")Student's t-Test (gleiche Varianzen):
t-Statistik: -23.6136
p-Wert: 0.000000000000000000000000000000000000000000000000000000000000
Ergebnis: Der Unterschied ist statistisch signifikant (p < 0.05)Die t-Statistik für den Student’s t-Test mit zwei unabhängigen Stichproben wird wie folgt berechnet:
\[t = \frac{\bar{x}_1 - \bar{x}_2}{s_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}\]
wobei \(\bar{x}_1\) und \(\bar{x}_2\) die Mittelwerte der beiden Stichproben sind, \(s_p\) die gepoolte Standardabweichung und \(n_1\) und \(n_2\) die jeweiligen Stichprobengrößen. Die gepoolte Standardabweichung ist:
\[s_p = \sqrt{\frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}}\]
Welch-Test (ungleiche Varianzen)
Der Welch-Test ist eine Variante des t-Tests, die keine gleichen Varianzen in den Gruppen voraussetzt. Er ist robuster als der Student’s t-Test und wird oft als Standard empfohlen:
# Welch-Test durchführen (equal_var=False)
t_stat_welch, p_value_welch = stats.ttest_ind(adelie, gentoo, equal_var=False)
print("Welch-Test (ungleiche Varianzen):")
print(f"t-Statistik: {t_stat_welch:.4f}")
print(f"p-Wert: {p_value_welch:.60f}")
if p_value_welch < 0.05:
print("Ergebnis: Der Unterschied ist statistisch signifikant (p < 0.05)")
else:
print("Ergebnis: Der Unterschied ist nicht statistisch signifikant (p >= 0.05)")Welch-Test (ungleiche Varianzen):
t-Statistik: -23.3860
p-Wert: 0.000000000000000000000000000000000000000000000000000000000000
Ergebnis: Der Unterschied ist statistisch signifikant (p < 0.05)Die t-Statistik für den Welch-Test wird ähnlich berechnet, aber die die Standardabweichung wird nicht gepoolt:
\[t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}\]
Die Freiheitsgrade werden ebenfalls anders1 berechnet (Welch-Satterthwaite-Approximation).
In unserem Fall liefern beide Tests ein ähnliches Ergebnis, da die Standardabweichungen der beiden Gruppen nicht stark voneinander abweichen. In der Praxis ist es jedoch oft ratsam, den Welch-Test zu verwenden, da er robuster ist und man zugleich nur wenig Leistungseinbußen hat.
Implementierung mit statsmodels
Neben scipy bietet auch statsmodels Funktionen für t-Tests, die zusätzliche Details liefern können:
from statsmodels.stats.weightstats import ttest_ind
# Ein-Stichproben-t-Test
### Keine analoge Funktion in statsmodels
# Gepaarter t-Test
### Keine analoge Funktion in statsmodels
# Student's t-Test
ttest_students = ttest_ind(adelie, gentoo, alternative='two-sided', usevar='pooled')
# Welch-Test
ttest_welch = ttest_ind(adelie, gentoo, alternative='two-sided', usevar='unequal')
# Ausgabe beispielhaft für Welch-Test
print("Welch-Test mit statsmodels:")
print(f"t-Statistik: {ttest_welch[0]:.4f}")
print(f"p-Wert: {ttest_welch[1]:.30f}")
print(f"Freiheitsgrade: {ttest_welch[2]:.2f}")Welch-Test mit statsmodels:
t-Statistik: -23.3860
p-Wert: 0.000000000000000000000000000000
Freiheitsgrade: 249.64Mit statsmodels könnten und werden wir auch einen t-Test als lineares Modell formulieren. Dies hilft uns, die Verbindung zwischen t-Tests und linearen Modellen zu verstehen, was uns wiederum im nächsten Kapitel zugutekommen wird. Dort beschäftigen wir uns damit, wie wir mit ANOVA mehrere Gruppen gleichzeitig vergleichen können.
Annahmen und nicht-parametrische Alternativen
Nun haben wir es in diesem Kapitel nicht explizit ausgesprochen, aber damit ein t-test gültig ist, müssen einige Annahmen erfüllt sein.
- Da ja die t-Verteilung zugrunde liegt gehen wir also mal wieder davon aus, dass die Daten normalverteilt sind bzw. aus einer normalverteilten Grundgesamtheit stammen.
- Bei den t-tests zum Vergleich unabhängiger Gruppen (Student’s und Welch) gehen wir außerdem davon aus, dass die Beobachtungen unabhängig sind. Das heißt, dass die Werte in einer Gruppe nicht von den Werten in der anderen Gruppe abhängen. Dem gegenüber stehen ja aber die gepaarten t-Tests, bei denen wir genau diese Abhängigkeit haben.
- Ähnlich verhält es sich mit der Annahme der Varianzhomogenität: Während der Student’s t-Test gleiche Varianzen in beiden Gruppen voraussetzt, trifft der Welch-Test diese Annahme eben nicht.
Darüber hinaus gibt es aber auch sogenannte nicht-parametrische Alternativen zu den t-Tests, die nämlich keine Annahmen über die Verteilung der Daten machen - also eben auch noch die erste der gerade genannten Annahmen nicht benötigen. Diese Tests sind dann nützlich, wenn die Daten nicht normalverteilt sind oder wenn die Stichprobengrößen sehr klein sind. Zu den bekanntesten gehören:
-
Wilcoxon-Vorzeichen-Rang-Test
- Alternative zum gepaarten t-Test:
wilcoxon(gewichte_vor, gewichte_nach) - oder auch Alternative zum Ein-Stichproben-t-Test:
scipy.stats.wilcoxon(adelie-4000) - Vergleicht zwei abhängige Stichproben ohne Normalverteilungsannahme, indem er die Ränge der Differenzen zwischen den Paaren analysiert.
- Alternative zum gepaarten t-Test:
-
Mann-Whitney-U-Test
- Alternative zum unabhängigen t-Test:
mannwhitneyu(adelie, gentoo, alternative='two-sided') - Vergleicht zwei unabhängige Stichproben ohne Normalverteilungsannahme, indem er die Ränge der Werte in beiden Gruppen analysiert.
- Auch als Wilcoxon-Rangsummentest bekannt.
- Alternative zum unabhängigen t-Test:
Diese nicht-parametrischen Tests sind demnach in Situationen einsetzbar, bei denen die Annahmen der t-Tests nicht erfüllt sind. Sie sind auch robuster gegenüber Ausreißern. Allerdings haben sie in der Regel eine geringere statistische Power als die parametrischen t-Tests, wenn die Annahmen für Letztere erfüllt sind. Es gilt also nur dann auf nicht-parametrische Tests zurückzugreifen, wenn die Annahmen für die t-Tests nicht erfüllt sind.
Zusammenfassung
In diesem Kapitel haben wir uns mit t-Tests befasst, einer der grundlegendsten und am häufigsten verwendeten Methoden zum Vergleich von Mittelwerten. Wir haben drei Haupttypen von t-Tests kennengelernt:
Ein-Stichproben-t-Test: Vergleicht einen Stichprobenmittelwert mit einem bekannten oder hypothetischen Referenzwert. Die t-Statistik wird berechnet als \(t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}}\).
Gepaarter t-Test: Vergleicht Messungen von denselben Subjekten zu zwei verschiedenen Zeitpunkten oder unter verschiedenen Bedingungen. Mathematisch ist dies ein Ein-Stichproben-t-Test auf die Differenzen: \(t = \frac{\bar{d}}{s_d / \sqrt{n}}\).
-
Unabhängiger t-Test: Vergleicht Mittelwerte zweier unabhängiger Gruppen.
- Student’s t-Test: Setzt gleiche Varianzen in beiden Gruppen voraus.
- Welch-Test: Robustere Variante für den Fall ungleicher Varianzen.
Für alle t-Tests müssen bestimmte Annahmen erfüllt sein, insbesondere:
- Normalverteilung der Daten (oder ausreichend große Stichproben)
- Bei unabhängigen t-Tests: Unabhängigkeit der Beobachtungen
- Bei Student’s t-Test: Gleiche Varianzen in beiden Gruppen
Wenn diese Annahmen nicht erfüllt sind, stehen nicht-parametrische Alternativen wie der Wilcoxon-Vorzeichen-Rang-Test (für gepaarte Daten) oder der Mann-Whitney-U-Test (für unabhängige Gruppen) zur Verfügung.
Die Entscheidung, welcher Test anzuwenden ist, hängt von der Struktur der Daten und der Forschungsfrage ab. Die korrekte Anwendung und Interpretation dieser Tests ist ein wesentlicher Bestandteil der statistischen Analyse in vielen wissenschaftlichen Disziplinen.
Übungen
Übung 1
In einer Studie zur Wirksamkeit eines neuen Blutdrucksenkungsmittels wurde der systolische Blutdruck von 25 Patienten vor und nach der Behandlung gemessen. Die durchschnittliche Blutdrucksenkung betrug 12 mmHg mit einer Standardabweichung der Differenzen von 8 mmHg.
- Welcher t-Test ist hier angemessen?
- Berechne die t-Statistik für diese Daten.
- Teste die Nullhypothese, dass die mittlere Blutdrucksenkung gleich 0 ist bei einem Signifikanzniveau von α = 0.05. Was ist deine Schlussfolgerung?
Übung 2
Ein Bildungsforscher möchte herausfinden, ob ein neues Lernprogramm die Mathematikleistung verbessert. Er testet zwei zufällig ausgewählte Gruppen von Schülern. Die erste Gruppe (n=40) erhält den traditionellen Unterricht und erreicht einen mittleren Testscore von 72 mit einer Standardabweichung von 8. Die zweite Gruppe (n=40) nimmt am neuen Lernprogramm teil und erreicht einen mittleren Testscore von 75 mit einer Standardabweichung von 9.
- Welchen t-Test würdest du hier anwenden?
- Berechne den Standardfehler der Differenz der Mittelwerte.
- Berechne ein 95%-Konfidenzintervall für die wahre mittlere Differenz der Testscores.
Übung 3
Ein Forscher möchte untersuchen, ob es einen Unterschied in der durchschnittlichen täglichen Bildschirmzeit zwischen Jugendlichen in städtischen und ländlichen Gebieten gibt. Er erhebt folgende Daten:
- Städtische Jugendliche (n=50): Mittlere Bildschirmzeit = 5.2 Stunden, Standardabweichung = 2.1 Stunden
- Ländliche Jugendliche (n=45): Mittlere Bildschirmzeit = 4.5 Stunden, Standardabweichung = 1.8 Stunden
- Formuliere geeignete Null- und Alternativhypothesen für diese Studie.
- Der p-Wert für diesen Test beträgt 0.08. Was ist die richtige Interpretation bei einem Signifikanzniveau von α = 0.05?
- Unter welchen Umständen wäre es besser, hier einen Welch-Test statt eines Student’s t-Tests zu verwenden?
Übung 4
Ein Hersteller von Autobatterien behauptet, dass seine Batterien eine durchschnittliche Lebensdauer von 60 Monaten haben. Ein unabhängiger Tester untersucht 18 zufällig ausgewählte Batterien und stellt fest, dass sie eine durchschnittliche Lebensdauer von 58.2 Monaten mit einer Standardabweichung von 3.5 Monaten haben.
- Formuliere die Nullhypothese und die Alternativhypothese für diesen Test.
- Berechne die t-Statistik für diesen Test.
- Bei einem Signifikanzniveau von α = 0.05 und 17 Freiheitsgraden, wie lautet die Schlussfolgerung?
Fußnoten
Beim Student’s t-Test werden die Freiheitsgrade einfach als \(df = n_1 + n_2 - 2\) berechnet (Abzug von 2 für die zwei geschätzten Mittelwerte). Beim Welch-Test dagegen werden die Freiheitsgrade mit der komplexeren Welch-Satterthwaite-Approximation berechnet: \(df_{Welch} = \frac{(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2})^2}{\frac{(\frac{s_1^2}{n_1})^2}{n_1-1} + \frac{(\frac{s_2^2}{n_2})^2}{n_2-1}}\). In beiden Fällen werden die Freiheitsgrade verwendet, um die entsprechende t-Verteilung zu bestimmen, anhand derer der p-Wert ermittelt wird.↩︎