import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
import statsmodels.api as sm
import statsmodels.formula.api as smf
np.random.seed(42) # für reproduzierbare ErgebnisseLogistische Regression
In den vorangegangenen Kapiteln haben wir uns intensiv mit linearen Modellen beschäftigt. All diese Methoden hatten eines gemeinsam: Sie versuchten, eine numerische Zielvariable vorherzusagen. Doch was passiert, wenn unsere Zielvariable nicht numerisch, sondern binär ist - wie Erfolg/Misserfolg, Anwesenheit/Abwesenheit oder - um mal wieder bei unseren Pinguinen zu bleiben - Adelie/Gentoo?
Hier kommt die logistische Regression ins Spiel. Sie ist eine Regressionsmethode für binäre Zielvariablen, die Wahrscheinlichkeiten schätzt. Konkret fragt sie “Wie hoch ist die Wahrscheinlichkeit, dass ein Pinguin mit Gewicht X ein Gentoo ist?”
Diese Wahrscheinlichkeiten können wir dann vielfältig nutzen: für statistische Inferenz und Hypothesentests, zur Quantifizierung von Unsicherheit, oder - wenn gewünscht und in Machine Learning üblich - für Klassifikation durch das Anwenden eines Schwellenwerts.
In der Statistik ist die logistische Regression seit den 1940er Jahren eine Regressionsmethode zur Analyse binärer Outcomes. Sie schätzt Wahrscheinlichkeiten und wird für Inferenz, Hypothesentests und Effektschätzung verwendet.
Im Machine Learning wird sie oft als “Klassifikationsalgorithmus” bezeichnet, da dort der Fokus auf der Vorhersage von Kategorien liegt. Dies geschieht durch einen zusätzlichen Schritt: Die geschätzten Wahrscheinlichkeiten werden mit einem Schwellenwert (meist 0.5) verglichen, um Klassifikationen zu erhalten.
Beide Sichtweisen sind berechtigt - wir werden in diesem Kapitel die statistische Perspektive als Ausgangspunkt nehmen und dann zeigen, wie daraus Klassifikation entstehen kann. So verstehen Sie sowohl die ursprüngliche Natur der Methode als auch ihre modernen Anwendungen.
Seid gewarnt und lasst euch nicht irritieren, dass viele Artikel/Posts/Videos zu diesem Thema oft nur aus einer der beiden Richtungen kommen und die jeweils andere mehr oder weniger ignorieren. Bei weitergehendem Interesse hierzug kann z.B. die Diskussion von Bruce Ratner und Adrian Olszweski hier und die darin angegebene URLs gelesen werden.
Der zentrale Unterschied zur linearen Regression: Während die lineare Regression eine gerade Linie an die Daten anpasst um numerische Werte vorherzusagen, passt die logistische Regression eine S-förmige Kurve an die Daten an, um Wahrscheinlichkeiten zwischen 0 und 1 zu modellieren.
Das Thema logistische Regression ist sehr populär und gleichzeitig kompliziert, sodass es viele gute Videos dazu gibt. Anders als in den vorangegangenen Kapiteln, sind deshalb in diesem Kapitel an mehreren Stellen Videos als Weitere Ressourcen angegeben - nicht nur wie sonst am Ende. Die Videos passen dann immer mehr oder weniger zu dem gerade gelesenen Abschnitt und erleichtern so idealerweise das Verständnis.
Ein binäres Regressionsproblem
Schauen wir uns zunächst an, wie ein typisches binäres Regressionsproblem aussieht. Wir verwenden dafür unseren bekannten Palmer Penguins Datensatz, fokussieren uns aber diesmal nur auf zwei Arten: Adelie und Gentoo.
Unser Regressionsziel: Wir wollen die Wahrscheinlichkeit modellieren, dass ein Pinguin zur Art Gentoo gehört, basierend auf seinem Körpergewicht. Da wir mathematisch nicht direkt mit den Kategorienamen “Adelie” und “Gentoo” arbeiten können, müssen wir zunächst eine numerische Kodierung vornehmen - ganz ähnlich wie bei der Dummy-Codierung in ANOVA-Modellen. Wir legen fest: Adelie = 0 und Gentoo = 1.
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
# Nur Gentoo und Adelie Pinguine, nur relevante Spalten
penguins_binary = penguins[penguins['species'].isin(['Gentoo', 'Adelie'])][['species', 'body_mass_g']].copy()
# Missing values entfernen
penguins_binary = penguins_binary.dropna(subset=['body_mass_g'])
# Binäre Zielvariable erstellen (0 = Adelie, 1 = Gentoo)
penguins_binary['species_binary'] = (penguins_binary['species'] == 'Gentoo').astype(int)
penguins_binary
print("Anzahl pro Kodierung:")
print(f"Adelie (0): {(penguins_binary['species_binary'] == 0).sum()}")
print(f"Gentoo (1): {(penguins_binary['species_binary'] == 1).sum()}") species body_mass_g species_binary
0 Adelie 3750.0 0
1 Adelie 3800.0 0
2 Adelie 3250.0 0
4 Adelie 3450.0 0
5 Adelie 3650.0 0
.. ... ... ...
270 Gentoo 4925.0 1
272 Gentoo 4850.0 1
273 Gentoo 5750.0 1
274 Gentoo 5200.0 1
275 Gentoo 5400.0 1
[274 rows x 3 columns]
Anzahl pro Kodierung:
Adelie (0): 151
Gentoo (1): 123Schauen wir uns zunächst an, wie die Daten aussehen, wenn wir die Arten als 0 und 1 kodieren:
Code zeigen/verstecken
fig, ax = plt.subplots(figsize=(9, 5), layout='tight')
# Separate Farben für die beiden Arten
adelie_mask = penguins_binary['species'] == 'Adelie'
gentoo_mask = penguins_binary['species'] == 'Gentoo'
ax.scatter(penguins_binary.loc[adelie_mask, 'body_mass_g'],
penguins_binary.loc[adelie_mask, 'species_binary'],
alpha=0.6, color=colors['Adelie'], label='Adelie', s=50)
ax.scatter(penguins_binary.loc[gentoo_mask, 'body_mass_g'],
penguins_binary.loc[gentoo_mask, 'species_binary'],
alpha=0.6, color=colors['Gentoo'], label='Gentoo', s=50)
ax.set_xlabel('Körpergewicht (g)')
ax.set_ylabel('Art (0=Adelie, 1=Gentoo)')
ax.set_title('Pinguinarten vs. Körpergewicht (numerisch kodiert)')
ax.set_ylim(-0.1, 1.1);
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
Abgesehen von der numerischen Kodierung der Arten kennen wir dieses Bild im Grunde schon: Sonst hatten wir lediglich die beiden Achsen vertauscht, die Punkte gejittert und den jeweiligen Mittelwert der Körpergewichte als gestrichelte Linie eingezeichnet.
Wir sehen also wieder deutlich: Generell sind Gentoo-Pinguine schwerer als Adelie-Pinguine. Aber es gibt auch Überlappungen - der leichteste Gentoo ist leichter als einige der schwersten Adelie-Pinguine. Das macht die Wahrscheinlichkeitsmodellierung interessant und sinnvoll: Bei mittleren Gewichten gibt es echte Unsicherheit über die Artzugehörigkeit.
Wahrscheinlichkeiten als Regressionsziel
Der entscheidende konzeptionelle Schritt der logistischen Regression: Anstatt direkt zu versuchen, die Kategorie (0 oder 1) vorherzusagen, modellieren wir die Wahrscheinlichkeit P(Y=1|X=x) - also die Wahrscheinlichkeit, dass ein Pinguin zur Art Gentoo gehört, gegeben sein Körpergewicht.
Diese Herangehensweise ist in mehrfacher Hinsicht vorteilhaft:
- Unsicherheitsquantifizierung: Statt nur “Das ist ein Gentoo” können wir sagen “Die Wahrscheinlichkeit, dass das ein Gentoo ist, beträgt 75%”
- Statistische Inferenz: Wir können Hypothesen über Effekte testen und Konfidenzintervalle berechnen
- Flexibilität: Die Wahrscheinlichkeiten können für verschiedene Zwecke genutzt werden - von Risikobewertung bis hin zu Klassifikation
Wahrscheinlichkeiten haben aber eine wichtige mathematische Eigenschaft: Sie müssen zwischen 0 (0%) und 1 (100%) liegen. Eine Wahrscheinlichkeit von -0.3 oder 1.7 ergibt schlichtweg keinen Sinn.
Genau hier liegt das Problem, wenn wir versuchen, eine einfache lineare Regression auf unser binäres Problem anzuwenden:
Das Problem mit linearer Regression bei Wahrscheinlichkeiten
Versuchen wir zunächst, eine lineare Regression zu verwenden, um die Wahrscheinlichkeit der Artzugehörigkeit basierend auf dem Körpergewicht zu schätzen. Wir interpretieren unsere binäre Kodierung (0 = Adelie, 1 = Gentoo) als Wahrscheinlichkeiten und versuchen, diese mit einer linearen Funktion zu modellieren:
# Lineare Regression mit statsmodels anpassen
linear_model = smf.ols('species_binary ~ body_mass_g', data=penguins_binary)
linear_result = linear_model.fit()
# Vorhersagelinie plotten
x_range = np.linspace(penguins_binary['body_mass_g'].min(),
penguins_binary['body_mass_g'].max(), 100)
y_pred_linear = linear_result.predict(pd.DataFrame({'body_mass_g': x_range}))Code zeigen/verstecken
fig, ax = plt.subplots(figsize=(9, 5), layout='tight')
# Scatter plot mit binärer Zielvariable
# Separate Farben für die beiden Arten
adelie_mask = penguins_binary['species'] == 'Adelie'
gentoo_mask = penguins_binary['species'] == 'Gentoo'
ax.scatter(penguins_binary.loc[adelie_mask, 'body_mass_g'],
penguins_binary.loc[adelie_mask, 'species_binary'],
alpha=0.6, color=colors['Adelie'], label='Adelie')
ax.scatter(penguins_binary.loc[gentoo_mask, 'body_mass_g'],
penguins_binary.loc[gentoo_mask, 'species_binary'],
alpha=0.6, color=colors['Gentoo'], label='Gentoo')
ax.plot(x_range, y_pred_linear, 'r-', linewidth=2, label='Lineare Regression')
ax.axhline(y=0.5, color='gray', linestyle='--', alpha=0.7, label='50%-Marke')
ax.set_xlabel('Körpergewicht (g)')
ax.set_ylabel('Wahrscheinlichkeit P(Gentoo)')
ax.set_title('Problem: Lineare Regression bei Wahrscheinlichkeiten')
# Y-Achse auf sinnvolle Werte beschränken
ax.set_ylim(-0.2, 1.2);
ax.legend()
plt.show()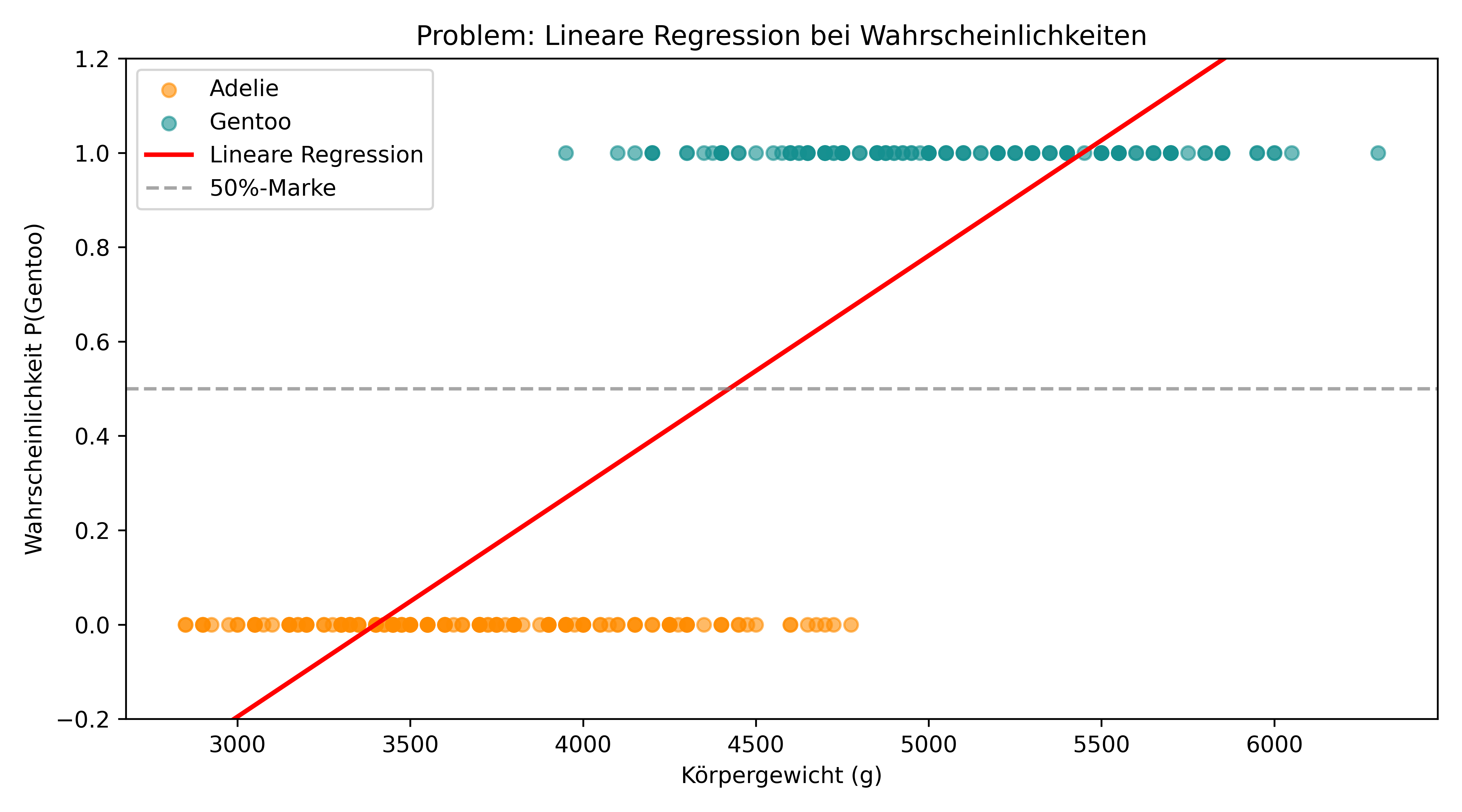
Das Problem wird sofort deutlich: Die lineare Regression kann Wahrscheinlichkeiten unter 0 und über 1 vorhersagen, was mathematisch unsinnig ist! Außerdem ist die Beziehung zwischen Körpergewicht und Artzugehörigkeit nicht wirklich linear - wir bräuchten eine S-förmige Kurve, die sich asymptotisch den Werten 0 und 1 nähert.
Grundkonzepte der logistischen Regression
Der Schlüssel zur logistischen Regression liegt darin, eine mathematische Transformation zu finden, die:
- Wahrscheinlichkeiten immer im Bereich [0, 1] hält
- Eine S-förmige Kurve erzeugt, die sich den Daten anpasst
- Im Hintergrund immer noch mit linearen Kombinationen arbeitet (wie die lineare Regression)
Von Wahrscheinlichkeiten zu Odds
Ein zentrales Konzept der logistischen Regression sind die Odds (Chancenverhältnisse). Die Odds sind das Verhältnis der Wahrscheinlichkeit, dass ein Ereignis eintritt, zu der Wahrscheinlichkeit, dass es nicht eintritt:
\[\text{Odds} = \frac{p}{1-p}\]
Wobei \(p\) hier die Wahrscheinlichkeit ist, dass ein Pinguin zur Art Gentoo gehört. Folgende Sätze verstehen sich von selbst, aber es soll trotzdem einmal ausgesprochen werden: Jeder Pinguin kann hier nur zu genau einer der beiden Arten gehören. Alle Punkte (=beobachteten Daten) werden demnach in der Abbildung oben immer nur bei genau 0 oder 1 liegen - niemals dazwischen.
Beispiel: Wenn die Wahrscheinlichkeit, dass ein Pinguin ein Gentoo ist, bei 0.75 liegt, dann sind die Odds: \[\text{Odds} = \frac{0.75}{1-0.75} = \frac{0.75}{0.25} = 3\]
Das bedeutet, die Chancen stehen 3:1 für Gentoo.
Code zeigen/verstecken
# Visualisierung: Wahrscheinlichkeit vs. Odds
p_values = np.linspace(0.01, 0.99, 100)
odds_values = p_values / (1 - p_values)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4), layout='tight')
# Wahrscheinlichkeiten
ax1.plot(p_values, p_values, 'b-', linewidth=2)
ax1.set_xlabel('Eingabe')
ax1.set_ylabel('Wahrscheinlichkeit')
ax1.set_title('Wahrscheinlichkeiten (beschränkt auf [0,1])')
ax1.grid(True, alpha=0.3)
# Odds
ax2.plot(p_values, odds_values, 'r-', linewidth=2)
ax2.set_xlabel('Wahrscheinlichkeit')
ax2.set_ylabel('Odds')
ax2.set_title('Odds (unbeschränkt, immer positiv)')
ax2.grid(True, alpha=0.3)
ax2.set_ylim(0, 20);
plt.show()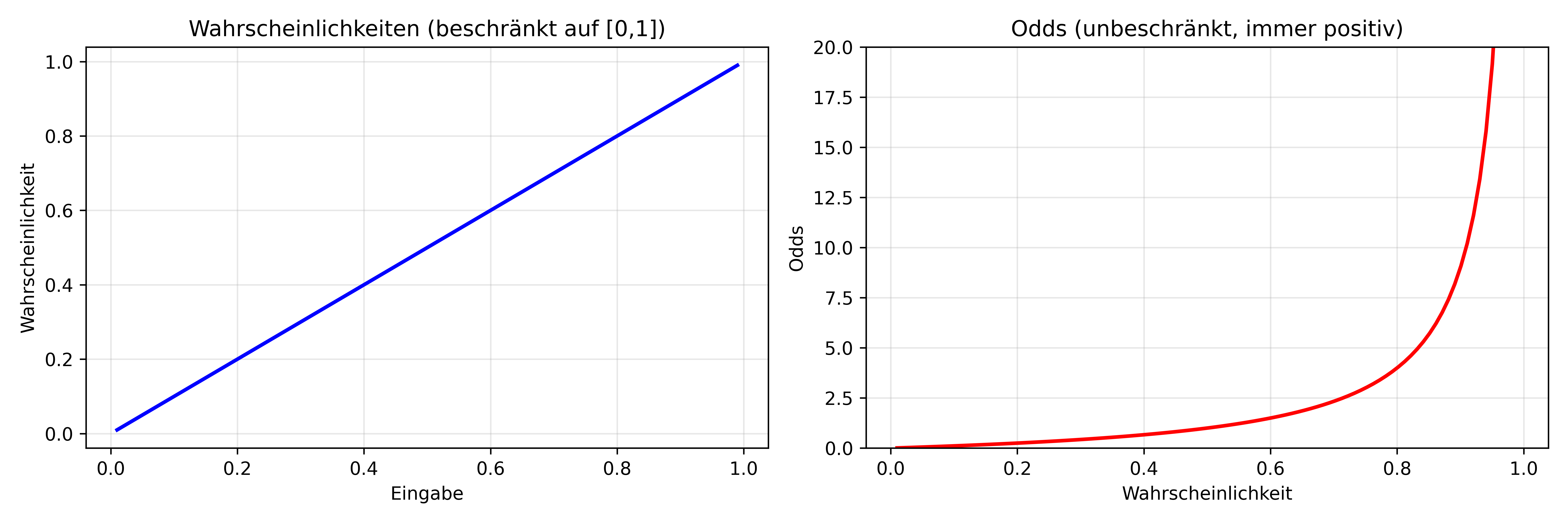
Die Logit-Transformation (Log-Odds)
Odds sind immer positiv, aber sie sind immer noch asymmetrisch verteilt. Der finale Schritt ist die Logit-Transformation: Wir nehmen den natürlichen Logarithmus der Odds:
\[\text{Logit}(p) = \ln\left(Odds\right) = \ln\left(\frac{p}{1-p}\right)\]
Diese Log-Odds (auch Logits genannt) können jeden reellen Wert annehmen von \(-\infty\) bis \(+\infty\). Das ist genau der Wertebereich, den wir für eine lineare Regression benötigen!
Code zeigen/verstecken
# Visualisierung der Logit-Transformation
p_values = np.linspace(0.01, 0.99, 100)
logit_values = np.log(p_values / (1 - p_values))
fig, ax = plt.subplots(figsize=(9, 5), layout='tight')
ax.plot(p_values, logit_values, 'g-', linewidth=2)
ax.axhline(y=0, color='gray', linestyle='--', alpha=0.7)
ax.axvline(x=0.5, color='gray', linestyle=':', alpha=0.7)
ax.set_xlabel('Wahrscheinlichkeit p')
ax.set_ylabel('Logit(p) = ln(p/(1-p))')
ax.set_title('Die Logit-Transformation')
ax.grid(True, alpha=0.3)
# Markante Punkte annotieren
ax.annotate('p=0.5 → Logit=0', xy=(0.5, 0), xytext=(0.7, -2),
arrowprops=dict(arrowstyle='->', color='red'),
fontsize=10, color='red')
plt.show()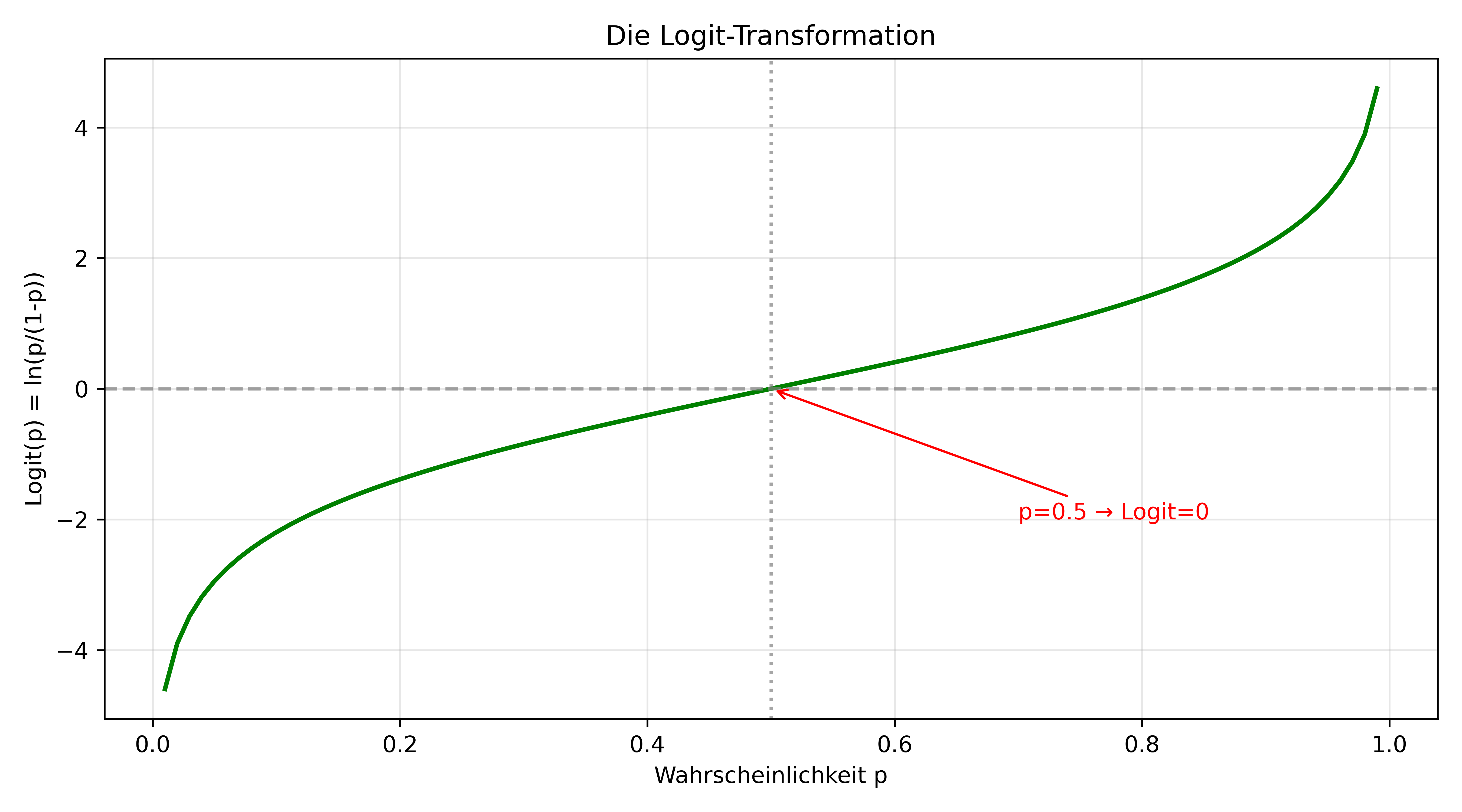
Die zentrale Erkenntnis: Die Logit-Transformation macht es möglich, eine lineare Beziehung zu modellieren:
\[\ln\left(\frac{p}{1-p}\right) = \text{Logit}(p) = \beta_0 + \beta_1 \cdot \text{Körpergewicht}\]
Die logistische Funktion
Um von den Logits schließlich zurück zu Wahrscheinlichkeiten als Regressionsziel zu gelangen, verwenden wir die logistische Funktion (auch Sigmoid-Funktion genannt):
\[p = \frac{1}{1 + e^{-(\beta_0 + \beta_1 \cdot x)}}\]
Diese Funktion erzeugt genau die S-förmige Kurve, die wir brauchen:
Code zeigen/verstecken
# Visualisierung der logistischen Funktion
x = np.linspace(-6, 6, 100)
y = 1 / (1 + np.exp(-x))
fig, ax = plt.subplots(figsize=(9, 5), layout='tight')
ax.plot(x, y, 'purple', linewidth=3, label='Logistische Funktion')
ax.axhline(y=0.5, color='gray', linestyle='--', alpha=0.7, label='p = 0.5')
ax.axvline(x=0, color='gray', linestyle=':', alpha=0.7, label='Logit = 0')
ax.set_xlabel('Logit-Wert')
ax.set_ylabel('Wahrscheinlichkeit')
ax.set_title('Die logistische Funktion: S-förmige Kurve')
ax.grid(True, alpha=0.3)
ax.legend()
plt.show()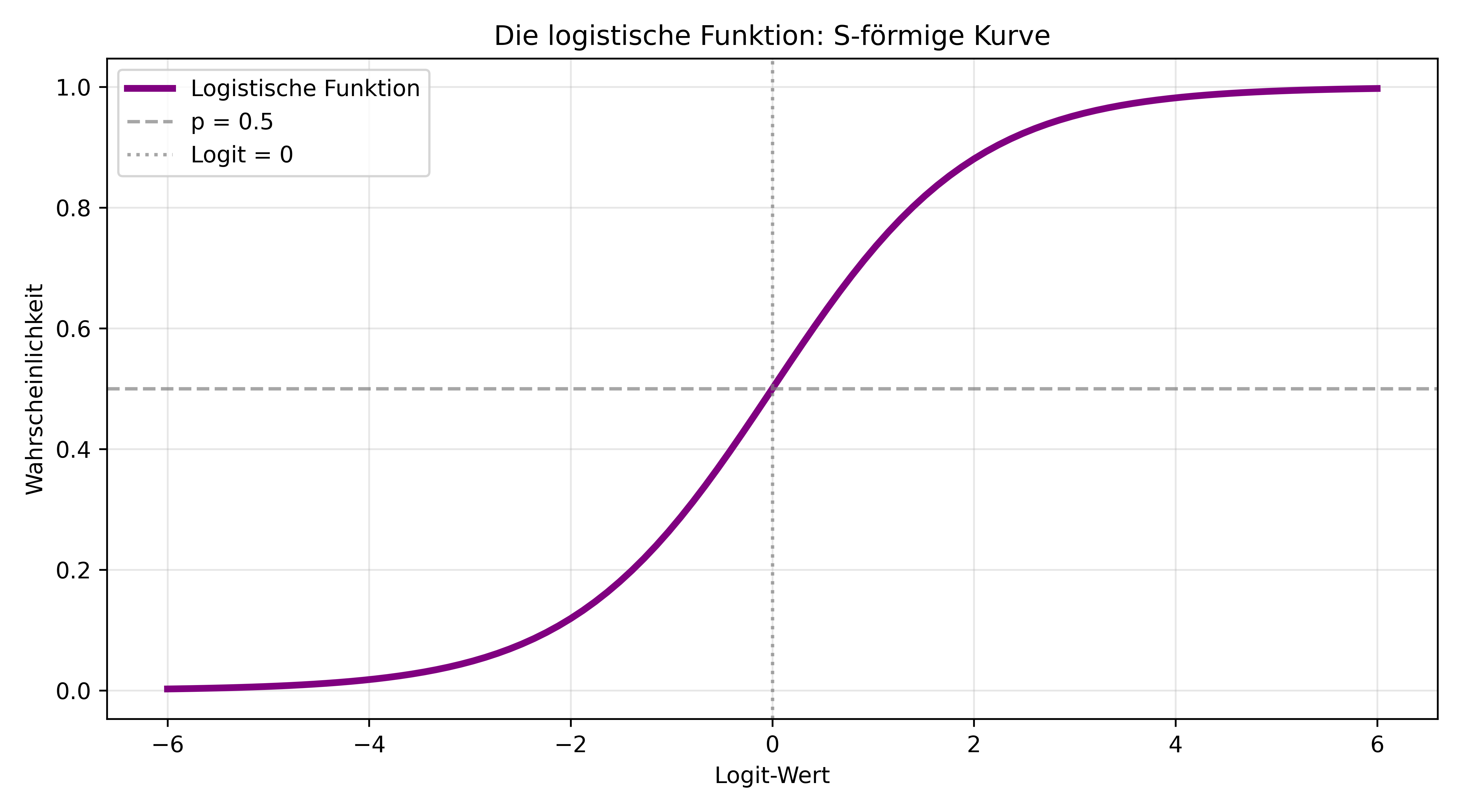
Implementierung der logistischen Regression
Jetzt implementieren wir die logistische Regression für unser Pinguin-Problem. Wir werden sowohl sklearn als auch statsmodels zeigen, aber dann bei statsmodels bleiben, da es mehr statistische Details liefert.
Mit scikit-learn
Zunächst ein kurzer Blick auf die sklearn-Implementation. Das Schöne an sklearn ist, dass die Syntax praktisch identisch zur linearen Regression ist - wir tauschen einfach LinearRegression() gegen LogisticRegression() aus:
# Daten vorbereiten
X = penguins_binary[['body_mass_g']]
y = penguins_binary['species_binary']
# Logistische Regression mit sklearn
log_reg_sklearn = LogisticRegression()
sklearn_fit = log_reg_sklearn.fit(X, y);
print("Sklearn Logistische Regression:")
print(f"Intercept (β₀): {log_reg_sklearn.intercept_[0]:.4f}")
print(f"Coefficient (β₁): {log_reg_sklearn.coef_[0][0]:.6f}")Sklearn Logistische Regression:
Intercept (β₀): -27.4819
Coefficient (β₁): 0.006229Die Ausgabe zeigt uns die geschätzten Parameter: einen Intercept von etwa -27.48 und einen Koeffizienten von etwa 0.0062 für das Körpergewicht. Diese Zahlen mögen auf den ersten Blick merkwürdig erscheinen, aber sie ergeben durchaus Sinn - dazu gleich mehr bei der Interpretation.
Mit statsmodels (unser Hauptansatz)
Während sklearn für maschinelles Lernen optimiert ist, bietet statsmodels deutlich mehr statistische Details - genau das, was wir für ein fundiertes Verständnis brauchen. Die Syntax ist wieder vertraut aus den linearen Modellen, nur verwenden wir jetzt smf.logit() statt smf.ols():
# Logistische Regression mit statsmodels
logit_model = smf.logit('species_binary ~ body_mass_g', data=penguins_binary)
logit_result = logit_model.fit()
# Zusammenfassung ausgeben
print(logit_result.summary())Optimization terminated successfully.
Current function value: 0.186255
Iterations 9
Logit Regression Results
==============================================================================
Dep. Variable: species_binary No. Observations: 274
Model: Logit Df Residuals: 272
Method: MLE Df Model: 1
Date: Di, 19 Aug 2025 Pseudo R-squ.: 0.7292
Time: 11:45:39 Log-Likelihood: -51.034
converged: True LL-Null: -188.49
Covariance Type: nonrobust LLR p-value: 9.654e-62
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
Intercept -27.4819 3.845 -7.148 0.000 -35.017 -19.946
body_mass_g 0.0062 0.001 7.161 0.000 0.005 0.008
===============================================================================Visualisierung des Modells
Um unser Modell zu begreifen ist es aber wohl noch hilfreicher, es zu visualisieren. Wir zeichnen die die Vorhersagen des Modells, also die S-förmige Kurve ein:
Code zeigen/verstecken
# Modell visualisieren
fig, ax = plt.subplots(figsize=(9, 5), layout='tight')
# Originaldaten
adelie_data = penguins_binary[penguins_binary['species'] == 'Adelie']
gentoo_data = penguins_binary[penguins_binary['species'] == 'Gentoo']
ax.scatter(adelie_data['body_mass_g'], adelie_data['species_binary'],
alpha=0.6, color=colors['Adelie'], label='Adelie', s=50)
ax.scatter(gentoo_data['body_mass_g'], gentoo_data['species_binary'],
alpha=0.6, color=colors['Gentoo'], label='Gentoo', s=50)
# Logistische Kurve
x_range = np.linspace(penguins_binary['body_mass_g'].min(),
penguins_binary['body_mass_g'].max(), 200)
predictions = logit_result.predict(pd.DataFrame({'body_mass_g': x_range}))
ax.plot(x_range, predictions, 'red', linewidth=3, label='Logistische Regression')
ax.axhline(y=0.5, color='gray', linestyle='--', alpha=0.7, label='50%-Marke')
ax.set_xlabel('Körpergewicht (g)')
ax.set_ylabel('Wahrscheinlichkeit P(Gentoo)')
ax.set_title('Logistische Regression: Wahrscheinlichkeitsschätzung')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()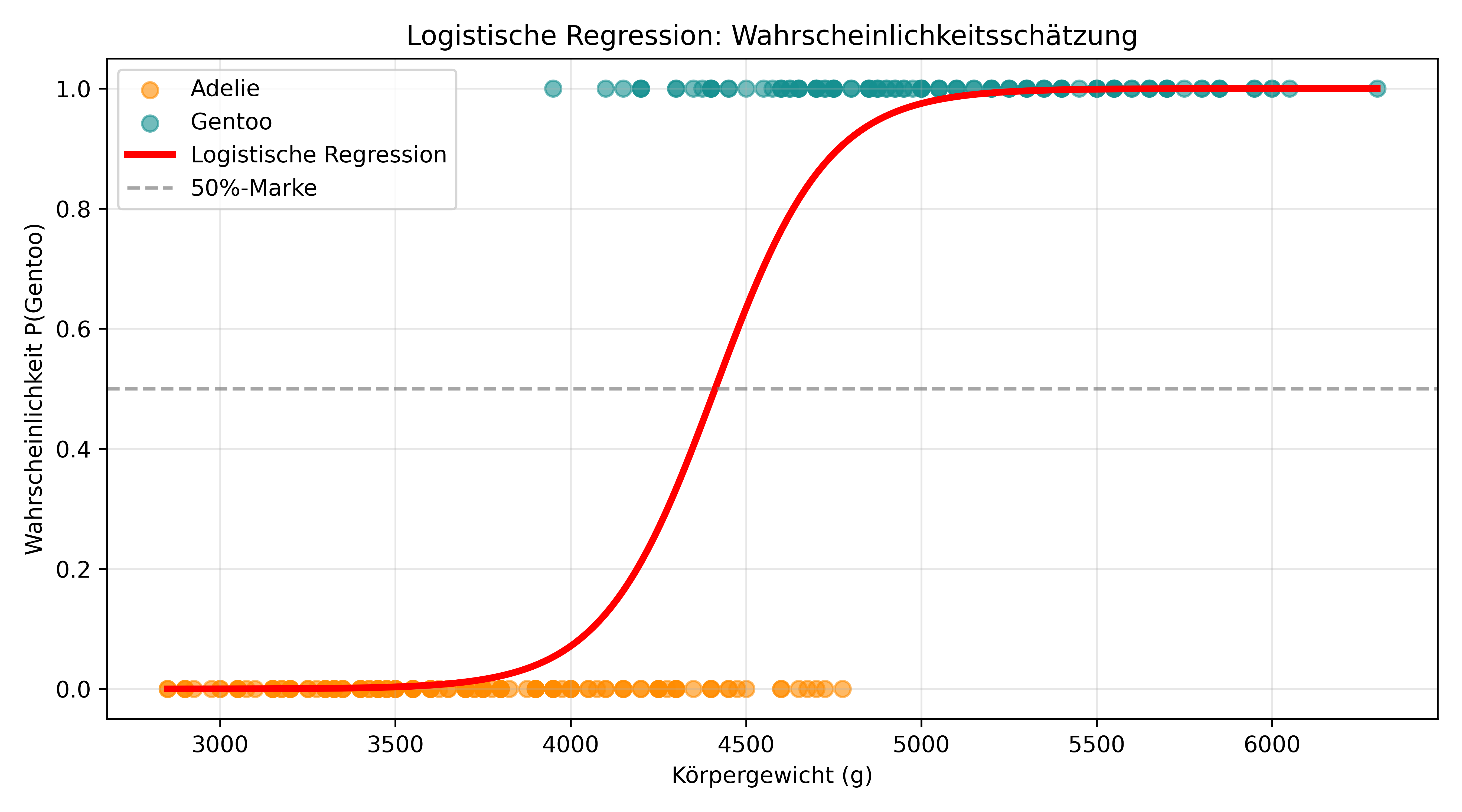
Wahrscheinlichkeitsschätzung und optionale Klassifikation
Nachdem wir unser Modell visuell verstanden haben, können wir es für konkrete Wahrscheinlichkeitsschätzungen einsetzen. Hierbei zeigt sich die Stärke der logistischen Regression: Sie liefert nicht nur Punkt-Schätzungen, sondern quantifiziert auch die Unsicherheit. Nehmen wir mal beispielhaft 3 Gewichte für die wir das anhand des Modells durchspielen: 4200g, 4500g und 5000g.
# Wahrscheinlichkeitsschätzungen
print("Wahrscheinlichkeitsschätzungen für verschiedene Körpergewichte:")
test_weights = [4200, 4500, 5000]
for weight in test_weights:
prob = logit_result.predict(pd.DataFrame({'body_mass_g': [weight]}))[0]
print(f"Gewicht {weight}g: P(Gentoo) = {prob:.3f}")Wahrscheinlichkeitsschätzungen für verschiedene Körpergewichte:
Gewicht 4200g: P(Gentoo) = 0.211
Gewicht 4500g: P(Gentoo) = 0.634
Gewicht 5000g: P(Gentoo) = 0.975Was sehen wir hier?
Entsprechend dem S-förmigen Verlauf der logistischen Funktion erhalten wir:
- 4200g: Mit 21% Wahrscheinlichkeit für Gentoo (wahrscheinlich ein Adelie)
- 4500g: Mit 63% Wahrscheinlichkeit für Gentoo (wahrscheinlich ein Gentoo)
- 5000g: Mit 98% Wahrscheinlichkeit für Gentoo (praktisch sicher ein Gentoo)
Diese Wahrscheinlichkeiten können wir auch grafisch veranschaulichen:
Code zeigen/verstecken
# Modell mit Vorhersagebeispielen visualisieren
fig, ax = plt.subplots(figsize=(9, 5), layout='tight')
# Originaldaten
adelie_data = penguins_binary[penguins_binary['species'] == 'Adelie']
gentoo_data = penguins_binary[penguins_binary['species'] == 'Gentoo']
ax.scatter(adelie_data['body_mass_g'], adelie_data['species_binary'],
alpha=0.6, color=colors['Adelie'], label='Adelie', s=50, zorder=3)
ax.scatter(gentoo_data['body_mass_g'], gentoo_data['species_binary'],
alpha=0.6, color=colors['Gentoo'], label='Gentoo', s=50, zorder=3)
# Logistische Kurve
x_range = np.linspace(penguins_binary['body_mass_g'].min(),
penguins_binary['body_mass_g'].max(), 200)
predictions = logit_result.predict(pd.DataFrame({'body_mass_g': x_range}))
ax.plot(x_range, predictions, 'red', linewidth=3, label='Logistische Regression', zorder=4)
ax.axhline(y=0.5, color='gray', linestyle=':', alpha=0.7, label='50%-Schwelle')
# Vorhersagebeispiele einzeichnen
test_weights = [4200, 4500, 5000]
test_probs = []
for weight in test_weights:
prob = logit_result.predict(pd.DataFrame({'body_mass_g': [weight]}))[0]
test_probs.append(prob)
# Punkt auf der Kurve
ax.plot(weight, prob, 'ko', markersize=8, markerfacecolor='yellow',
markeredgecolor='black', markeredgewidth=2, zorder=5)
# Vertikale Linie zur x-Achse
ax.plot([weight, weight], [0, prob], 'k--', alpha=0.5)
# Horizontale Linie zur y-Achse
ax.plot([penguins_binary['body_mass_g'].min(), weight], [prob, prob], 'k--', alpha=0.5)
# Beschriftung
ax.annotate(f'{weight}g\nP={prob:.2f}',
xy=(weight, prob), xytext=(weight+30, prob),
fontsize=9, ha='left', va='top')
ax.set_xlabel('Körpergewicht (g)')
ax.set_ylabel('Wahrscheinlichkeit P(Gentoo)')
ax.set_title('Logistische Regression: Wahrscheinlichkeitsschätzung mit Beispielen')
ax.legend(loc='center right', bbox_to_anchor=(1, 0.25), fontsize=9)
ax.grid(True, alpha=0.3)
plt.show()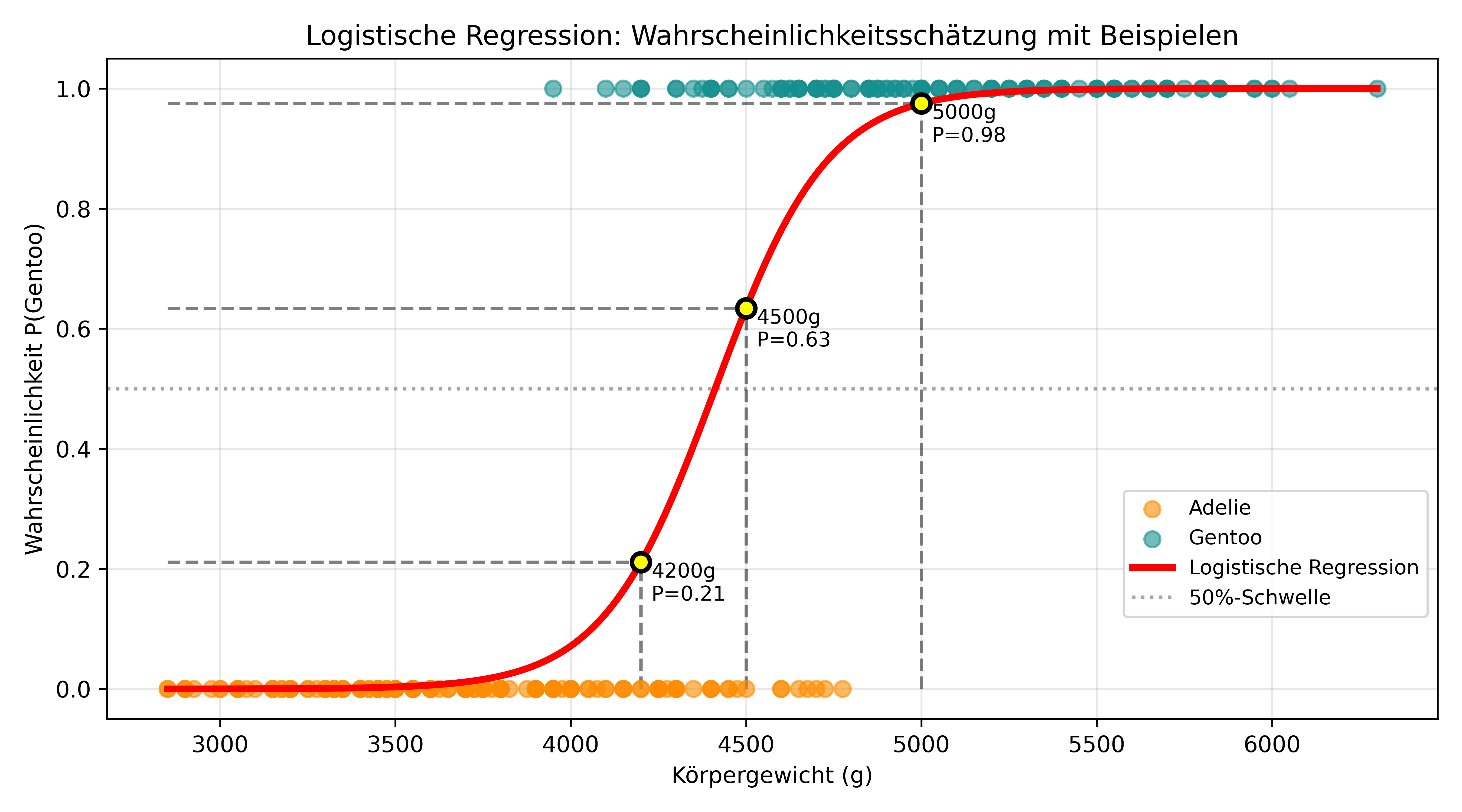
Diese Wahrscheinlichkeiten spiegeln die biologische Realität wider: Sehr leichte Pinguine sind fast immer Adelies, sehr schwere fast immer Gentoos, und im mittleren Bereich gibt es Überlappungen mit entsprechender Unsicherheit.
Von Wahrscheinlichkeiten zu Klassifikation
Wenn wir - etwa für Machine Learning Anwendungen - aus den Wahrscheinlichkeiten Klassifikationen ableiten möchten, können wir einen Schwellenwert anwenden. Der Standard ist meist 0.5:
# Klassifikation durch Schwellenwert
print("Von Wahrscheinlichkeiten zu Klassifikationen:")
test_weights = [4200, 4500, 5000]
for weight in test_weights:
prob = logit_result.predict(pd.DataFrame({'body_mass_g': [weight]}))[0]
classification = "Gentoo" if prob >= 0.5 else "Adelie"
print(f"Gewicht {weight}g: P(Gentoo) = {prob:.3f} → Klassifikation: {classification}")Von Wahrscheinlichkeiten zu Klassifikationen:
Gewicht 4200g: P(Gentoo) = 0.211 → Klassifikation: Adelie
Gewicht 4500g: P(Gentoo) = 0.634 → Klassifikation: Gentoo
Gewicht 5000g: P(Gentoo) = 0.975 → Klassifikation: GentooWichtig zu verstehen: Die Klassifikation ist ein zusätzlicher Schritt, der auf der Wahrscheinlichkeitsschätzung aufbaut. Die logistische Regression selbst schätzt Wahrscheinlichkeiten - die Klassifikation entsteht erst durch den Schwellenwert.
Die Entscheidungsgrenze
Eine wichtige Frage bei der optionalen Klassifikation ist: Wo ziehen wir die Grenze? Bei welcher Wahrscheinlichkeit entscheiden wir uns für Gentoo statt Adelie?
Die Standardregel ist einfach: Bei einer Wahrscheinlichkeit ≥ 0.5 klassifizieren wir als Gentoo, darunter als Adelie. Aber man kann diese Grenze je nach Problem anpassen:
# Verschiedene Entscheidungsgrenzen testen
decision_thresholds = [0.3, 0.5, 0.7]
print("Entscheidungsgrenze und Klassifikation für 4500g Pinguin:")
test_weight = 4500
prob = logit_result.predict(pd.DataFrame({'body_mass_g': [test_weight]}))[0]
for threshold in decision_thresholds:
classification = "Gentoo" if prob >= threshold else "Adelie"
print(f"Schwelle {threshold}: P={prob:.3f} → {classification}")Entscheidungsgrenze und Klassifikation für 4500g Pinguin:
Schwelle 0.3: P=0.634 → Gentoo
Schwelle 0.5: P=0.634 → Gentoo
Schwelle 0.7: P=0.634 → AdelieWarum könnte man die Grenze anpassen?
- Konservative Klassifikation (höhere Grenze): Wenn es sehr wichtig ist, keine falschen Gentoo-Klassifikationen zu machen
- Aggressive Klassifikation (niedrigere Grenze): Wenn es wichtig ist, möglichst alle Gentoos zu finden, auch wenn dabei einige Adelies fälschlicherweise als Gentoo klassifiziert werden
Diese Überlegungen führen uns zu wichtigen Konzepten wie Sensitivität, Spezifität und ROC-Kurven, die wir in späteren Kapiteln behandeln werden.
Interpretation der Koeffizienten und statistische Tests
Nachdem wir gesehen haben, wie unser Modell Wahrscheinlichkeiten schätzt, wollen wir verstehen, was die Koeffizienten bedeuten und wie die statistischen Tests funktionieren. Das ist der Punkt, wo sich die logistische Regression von der linearen Regression am deutlichsten unterscheidet.
Koeffizienten verstehen
# Koeffizienten extrahieren
beta0 = logit_result.params['Intercept']
beta1 = logit_result.params['body_mass_g']
print("Interpretation der Koeffizienten:")
print(f"β₀ (Intercept): {beta0:.4f}")
print(f"β₁ (Körpergewicht): {beta1:.6f}")
print()
# Beispielrechnung für einen 4200g Pinguin
mass_example = 4200
logit_value = beta0 + beta1 * mass_example
prob_gentoo = 1 / (1 + np.exp(-logit_value))
print(f"Beispiel: Pinguin mit {mass_example}g Körpergewicht")
print(f"Logit-Wert: {logit_value:.4f}")
print(f"Wahrscheinlichkeit Gentoo: {prob_gentoo:.4f} ({prob_gentoo*100:.1f}%)")Interpretation der Koeffizienten:
β₀ (Intercept): -27.4819
β₁ (Körpergewicht): 0.006229
Beispiel: Pinguin mit 4200g Körpergewicht
Logit-Wert: -1.3193
Wahrscheinlichkeit Gentoo: 0.2109 (21.1%)Was bedeuten diese Zahlen?
Nochmal zur Erinnerung - Wir modellieren wie folgt und könnten demnach einfach ausgedrückt sagen, dass der uns bekannte Teil eines linearen Modells nur da oben in der Klammer steht: \[p = \frac{1}{1 + e^{-(\beta_0 + \beta_1 \cdot x)}}\]
β₀ = -27.48: Das ist der Logit-Wert wenn das Körpergewicht 0g beträgt (theoretisch). Dieser extrem negative Wert bedeutet, dass die Wahrscheinlichkeit für einen 0g-Pinguin, ein Gentoo zu sein, praktisch null ist - was biologisch mehr oder weniger Sinn macht!
β₁ = 0.0062: Für jedes zusätzliche Gramm Körpergewicht steigt der Logit-Wert um 0.0062. Das klingt nach wenig, aber da Logit-Werte exponentiell in Wahrscheinlichkeiten umgewandelt werden, kann dieser kleine Wert bei größeren Gewichtsunterschieden einen großen Effekt haben.
Das ergibt demnach: \[p = \frac{1}{1 + e^{-(-27.48 + 0.0062 \cdot 4200)}} = \frac{1}{1 + e^{-(-1.32)}} = \frac{1}{1 + 3.74} = 0.211 \]
Konkret sehen wir: Ein 4200g Pinguin hat einen Logit-Wert von etwa -1.32, was einer Wahrscheinlichkeit von nur 21.1% entspricht, ein Gentoo zu sein.
Odds Ratios - die intuitivere Interpretation
Es ist ein wenig Geschmackssache, aber Odds Ratios können für Einige verständlicher als die Koeffizienten selbst sein, da sie direkte Aussagen über Effektstärken erlauben. Die Umwandlung von Logit-Koeffizienten zu Odds Ratios erfolgt durch die Exponentialfunktion:
\[\text{Odds Ratio} = e^{\beta_1}\]
# Odds Ratios berechnen
odds_ratios = np.exp(logit_result.params)
print("Odds Ratios:")
print(f"Intercept: {odds_ratios['Intercept']:.15f}")
print(f"Körpergewicht: {odds_ratios['body_mass_g']:.6f}")Odds Ratios:
Intercept: 0.000000000001161
Körpergewicht: 1.006249Was bedeutet das konkret?
Ein Odds Ratio von 1.006 für das Körpergewicht bedeutet: Für jedes zusätzliche Gramm Körpergewicht werden die Odds um den Faktor 1.006 multipliziert.
Rechnen wir das für zwei konkrete Pinguine durch:
- Pinguin A: 4200g → Odds = p/(1-p) = 0.211/(1-0.211) = 0.267
- Pinguin B: 4201g (1g schwerer) → neue Odds = 0.267 × 1.006 = 0.269
Das ist nur ein winziger Unterschied! Deshalb betrachten wir größere Gewichtsunterschiede:
\[\text{Odds Ratio für 100g} = 1.006^{100} = 1.86\]
Das bedeutet: Ein Pinguin, der 100g schwerer ist, hat 1.86-mal höhere Odds, ein Gentoo zu sein.
Konkret gerechnet:
- Pinguin C: 4200g → Odds = 0.267
- Pinguin D: 4300g (100g schwerer) → Odds = 0.267 × 1.86 = 0.497
Für noch größere Unterschiede:
\[\text{Odds Ratio für 500g} = 1.006^{500} = 22.5\]
Ein Pinguin, der 500g schwerer ist, hat 22.5-mal höhere Odds, ein Gentoo zu sein!
Maximum Likelihood Estimation
Jetzt ist es an der Zeit zu verstehen, wie diese Koeffizienten überhaupt entstanden sind! Anders als bei der linearen Regression, wo wir die “kleinsten Quadrate” verwenden, wird die logistische Regression mittels Maximum Likelihood Estimation (MLE) angepasst. Das ist ein fundamentaler Unterschied, der auch erklärt, warum die statistischen Tests anders funktionieren!
Die Grundidee
MLE sucht die Parameter β₀ und β₁, die die beobachteten Daten am wahrscheinlichsten machen. Das funktioniert, indem so lange Likelihoods für verschiedene Werte für die Parameter β₀ und β₁ berechnet wird, bis man die optimalen Werte gefunden hat. Für jeden Datenpunkt berechnen wir:
- Wenn der Pinguin ein Gentoo ist (y=1): Die Wahrscheinlichkeit p
- Wenn der Pinguin ein Adelie ist (y=0): Die Wahrscheinlichkeit (1-p)
Die Likelihood ist das Produkt aller individuellen Wahrscheinlichkeiten:
\[L(\beta_0, \beta_1) = \prod_{i=1}^{n} p_i^{y_i} \cdot (1-p_i)^{1-y_i}\]
Da Produkte numerisch problematisch sind, verwenden wir die Log-Likelihood:
\[\ell(\beta_0, \beta_1) = \sum_{i=1}^{n} [y_i \ln(p_i) + (1-y_i) \ln(1-p_i)]\]
Ein konkretes Likelihood-Beispiel
Bevor wir das große Optimierungsproblem visualisieren, schauen wir uns an einem einfachen Beispiel an, wie die Likelihood-Berechnung funktioniert. Nehmen wir nur 4 Pinguine aus unserem Datensatz:
# 4 Beispiel-Pinguine auswählen (2 Adelies, 2 Gentoos)
adelie_indices = penguins_binary[penguins_binary['species'] == 'Adelie'].index[:2]
gentoo_indices = penguins_binary[penguins_binary['species'] == 'Gentoo'].index[:2]
example_indices = list(adelie_indices) + list(gentoo_indices)
example_penguins = penguins_binary.loc[example_indices].copy()
print("Unsere Beispiel-Pinguine:")
print(example_penguins[['body_mass_g', 'species', 'species_binary']])Unsere Beispiel-Pinguine:
body_mass_g species species_binary
0 3750.0 Adelie 0
1 3800.0 Adelie 0
152 4500.0 Gentoo 1
153 5700.0 Gentoo 1Jetzt testen wir genau zwei Parameter-Kombinationen und berechnen für jede die Likelihood:
- Erst probieren wir \(\beta_0\)=-20 und \(\beta_1\)=0.004
- Danach probieren wir \(\beta_0\)=-27 und \(\beta_1\)=0.006
# Zwei verschiedene Parameter-Kombinationen testen
params_1 = {'beta0': -20, 'beta1': 0.004} # Schlechtere Werte
params_2 = {'beta0': -27, 'beta1': 0.006} # Bessere Werte (näher am Optimum)
def calculate_likelihood_step_by_step(beta0, beta1, penguins_df):
"""Berechnet Likelihood Schritt für Schritt"""
print(f"\nBerechnung für β₀ = {beta0}, β₁ = {beta1}")
print("=" * 50)
likelihood = 1.0 # Startwert für Multiplikation
log_likelihood = 0.0 # Startwert für Summation
for i, (idx, penguin) in enumerate(penguins_df.iterrows()):
# Logit-Wert berechnen
logit = beta0 + beta1 * penguin['body_mass_g']
# Wahrscheinlichkeit für Gentoo
p_gentoo = 1 / (1 + np.exp(-logit))
# Tatsächliche Beobachtung
is_gentoo = penguin['species_binary']
species_name = penguin['species']
# Wahrscheinlichkeit für diese Beobachtung
if is_gentoo == 1:
prob_this_obs = p_gentoo
prob_explanation = f"P(Gentoo) = {p_gentoo:.4f}"
else:
prob_this_obs = 1 - p_gentoo
prob_explanation = f"P(Adelie) = 1 - {p_gentoo:.4f} = {prob_this_obs:.4f}"
print(f"Pinguin {i+1}: {penguin['body_mass_g']}g, tatsächlich {species_name}")
print(f" Logit = {beta0} + {beta1} × {penguin['body_mass_g']} = {logit:.3f}")
print(f" {prob_explanation}")
print(f" → Likelihood-Beitrag: {prob_this_obs:.4f}")
# Zur Gesamt-Likelihood hinzufügen
likelihood *= prob_this_obs
log_likelihood += np.log(prob_this_obs)
print(f"\nGesamt-Likelihood: {likelihood:.8f}")
print(f"Log-Likelihood: {log_likelihood:.4f}")
return likelihood, log_likelihood
# Parameter-Set 1 testen
ll1, log_ll1 = calculate_likelihood_step_by_step(
params_1['beta0'], params_1['beta1'], example_penguins
)
# Parameter-Set 2 testen
ll2, log_ll2 = calculate_likelihood_step_by_step(
params_2['beta0'], params_2['beta1'], example_penguins
)
print(f"\n" + "="*60)
print("VERGLEICH:")
print(f"Parameter-Set 1: Likelihood = {ll1:.8f}, Log-Likelihood = {log_ll1:.4f}")
print(f"Parameter-Set 2: Likelihood = {ll2:.8f}, Log-Likelihood = {log_ll2:.4f}")
print(f"\nParameter-Set 2 ist {'besser' if log_ll2 > log_ll1 else 'schlechter'}!")
print(f"Unterschied in Log-Likelihood: {log_ll2 - log_ll1:.4f}")
Berechnung für β₀ = -20, β₁ = 0.004
==================================================
Pinguin 1: 3750.0g, tatsächlich Adelie
Logit = -20 + 0.004 × 3750.0 = -5.000
P(Adelie) = 1 - 0.0067 = 0.9933
→ Likelihood-Beitrag: 0.9933
Pinguin 2: 3800.0g, tatsächlich Adelie
Logit = -20 + 0.004 × 3800.0 = -4.800
P(Adelie) = 1 - 0.0082 = 0.9918
→ Likelihood-Beitrag: 0.9918
Pinguin 3: 4500.0g, tatsächlich Gentoo
Logit = -20 + 0.004 × 4500.0 = -2.000
P(Gentoo) = 0.1192
→ Likelihood-Beitrag: 0.1192
Pinguin 4: 5700.0g, tatsächlich Gentoo
Logit = -20 + 0.004 × 5700.0 = 2.800
P(Gentoo) = 0.9427
→ Likelihood-Beitrag: 0.9427
Gesamt-Likelihood: 0.11070655
Log-Likelihood: -2.2009
Berechnung für β₀ = -27, β₁ = 0.006
==================================================
Pinguin 1: 3750.0g, tatsächlich Adelie
Logit = -27 + 0.006 × 3750.0 = -4.500
P(Adelie) = 1 - 0.0110 = 0.9890
→ Likelihood-Beitrag: 0.9890
Pinguin 2: 3800.0g, tatsächlich Adelie
Logit = -27 + 0.006 × 3800.0 = -4.200
P(Adelie) = 1 - 0.0148 = 0.9852
→ Likelihood-Beitrag: 0.9852
Pinguin 3: 4500.0g, tatsächlich Gentoo
Logit = -27 + 0.006 × 4500.0 = 0.000
P(Gentoo) = 0.5000
→ Likelihood-Beitrag: 0.5000
Pinguin 4: 5700.0g, tatsächlich Gentoo
Logit = -27 + 0.006 × 5700.0 = 7.200
P(Gentoo) = 0.9993
→ Likelihood-Beitrag: 0.9993
Gesamt-Likelihood: 0.48683721
Log-Likelihood: -0.7198
============================================================
VERGLEICH:
Parameter-Set 1: Likelihood = 0.11070655, Log-Likelihood = -2.2009
Parameter-Set 2: Likelihood = 0.48683721, Log-Likelihood = -0.7198
Parameter-Set 2 ist besser!
Unterschied in Log-Likelihood: 1.4810Was sehen wir hier?
- Für jeden Pinguin berechnen wir die Wahrscheinlichkeit der beobachteten Art
- Likelihood = Produkt aller individuellen Wahrscheinlichkeiten
- Log-Likelihood = Summe aller logarithmierten Wahrscheinlichkeiten
- Höhere Log-Likelihood = bessere Parameter (weniger negative Werte)
Wichtige Erkenntnis: Die “besten” Parameter hängen von den konkreten Daten ab! In diesem kleinen Beispiel kann ein Parameter-Set besser sein, das im Gesamtdatensatz schlechter wäre. MLE findet die Parameter, die für alle ~270 Pinguine optimal sind.
Warum werden die Likelihoods so klein? Weil wir Wahrscheinlichkeiten (alle < 1) multiplizieren! Deshalb arbeiten wir mit Log-Likelihoods - die werden nicht so winzig.
Das Optimierungsproblem: Nun haben wir ja aber einfach zwei Parameter-Sets ausprobiert und haben kein Gefühl dafür wie viele wir noch ausprobieren sollen. Es ist ein wenig wie Topfschlagen: In eine neue Richtung zu klopfen ist wie neue Parameter auszuprobieren und die Information des “Wärmer!/Kälter!” steckt in der likelihood. Leider macht es aber nicht automatisch Ding, weil man irgendwann mit einem Löffel auf den Topf haut. Stattdessen muss man merken wan man sich an einem Punkt befindet, von dem aus in jede Richtung nur noch kälter wird.
MLE sucht automatisch in dem riesigen Raum aller möglichen β₀ und β₁ Kombinationen nach derjenigen, die die höchste Log-Likelihood ergibt. Bei unserem echten Datensatz mit ~270 Pinguinen!
Das Optimierungsproblem visualisieren
Um zu verstehen, wie MLE funktioniert, visualisieren wir die Log-Likelihood-Oberfläche um die optimalen Parameter herum:
Code zeigen/verstecken
# 3D-Visualisierung der Log-Likelihood-Oberfläche
from mpl_toolkits.mplot3d import Axes3D
# Optimale Parameter (aus unserem Modell)
optimal_beta0 = logit_result.params['Intercept']
optimal_beta1 = logit_result.params['body_mass_g']
print(f"Optimale Parameter:")
print(f"β₀ (Intercept): {optimal_beta0:.4f}")
print(f"β₁ (Körpergewicht): {optimal_beta1:.6f}")
print(f"Log-Likelihood am Optimum: {logit_result.llf:.2f}")
# Log-Likelihood Funktion definieren
def compute_log_likelihood(beta0, beta1, X, y):
"""Berechnet die Log-Likelihood für gegebene Parameter"""
logits = beta0 + beta1 * X
p = 1 / (1 + np.exp(-logits))
p = np.clip(p, 1e-10, 1-1e-10) # Numerische Stabilität
log_likelihood = np.sum(y * np.log(p) + (1-y) * np.log(1-p))
return log_likelihood
# Daten vorbereiten
X_vals = penguins_binary['body_mass_g'].values
y_vals = penguins_binary['species_binary'].values
# Parameter-Bereiche um das Optimum herum
beta0_range = np.linspace(optimal_beta0 - 2, optimal_beta0 + 2, 20)
beta1_range = np.linspace(optimal_beta1 - 0.001, optimal_beta1 + 0.001, 20)
# Meshgrid für 3D-Plot
B0, B1 = np.meshgrid(beta0_range, beta1_range)
# Log-Likelihood für alle Parameter-Kombinationen berechnen
LL = np.zeros_like(B0)
for i in range(B0.shape[0]):
for j in range(B0.shape[1]):
LL[i, j] = compute_log_likelihood(B0[i, j], B1[i, j], X_vals, y_vals)
# 3D-Plot erstellen
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
# Oberfläche plotten
surface = ax.plot_surface(B0, B1, LL, alpha=0.6, cmap='viridis')
# Optimalen Punkt markieren
ax.scatter([optimal_beta0], [optimal_beta1], [logit_result.llf],
color='red', s=100, label='Optimum')
# Beschriftungen
ax.set_xlabel('β₀ (Intercept)')
ax.set_ylabel('β₁ (Körpergewicht)')
ax.set_zlabel('Log-Likelihood')
ax.set_title('Log-Likelihood-Oberfläche der logistischen Regression')
# Colorbar hinzufügen
plt.colorbar(surface, shrink=0.5, aspect=5)
ax.legend()
plt.show()Optimale Parameter:
β₀ (Intercept): -27.4819
β₁ (Körpergewicht): 0.006229
Log-Likelihood am Optimum: -51.03
<matplotlib.colorbar.Colorbar object at 0x0000025DC2CB5790>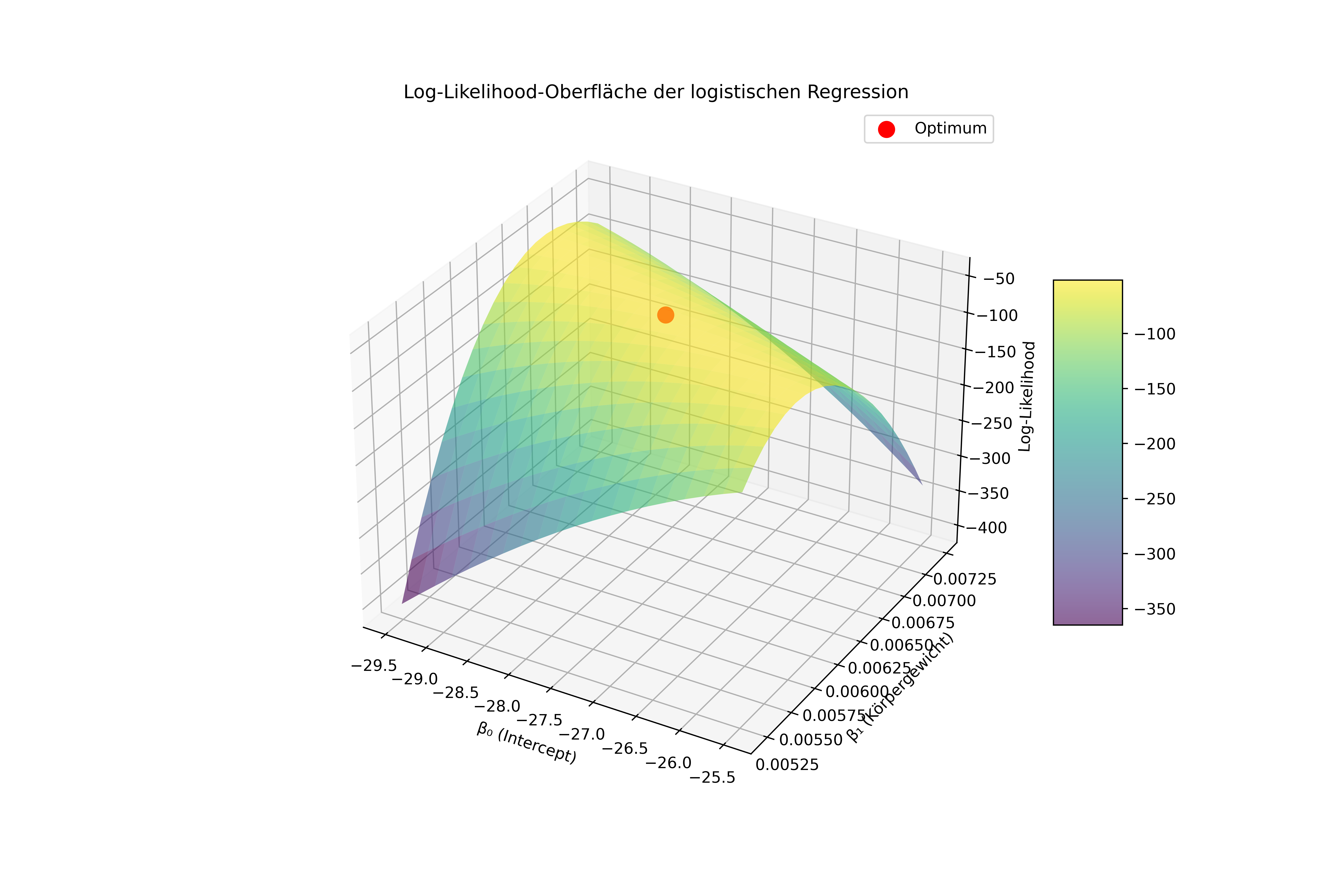
Was sehen wir hier?
Die Log-Likelihood-Oberfläche zeigt ein Maximum bei unseren optimalen Parametern. MLE findet automatisch diese Spitze - den Punkt, wo die Daten am wahrscheinlichsten sind.
Beachten Sie: - Die Oberfläche ist konkav (nach unten gewölbt) - das garantiert ein eindeutiges Maximum - Kleine Änderungen der Parameter führen zu deutlich schlechteren Log-Likelihood-Werten - Der rote Punkt zeigt das gefundene Optimum
Der iterative Optimierungsprozess
MLE hat also keine geschlossene Lösung wie die lineare Regression. Man berechnet nicht in einem Schwung die bestmöglichen Werte für die Parameter, sondern man probiert eben so lange aus, bis man die optimalen gefunden hat. Jedes neue Ausprobieren von Werten nennt man dabei eine Iteration. Das geschieht oft so schnell und vollautomatisch in Python, dass man es gar nicht bemerkt. Einen Punkt zu erreichen, an dem man die Parameterkombination als zufriedenstellend optimal ansieht nennt man Konvergenz bzw. das Modell konvergiert.
Man kann sich denken, dass man bei komplexeren Modellen und/oder größeren Datensätzen auch an einen Punkt gelangen kann, wo das Berechnen der Likelihood für eine Iteration z.B. mehrere Sekunden dauert und dann auch dutzende Male iteriert werden muss, bis der Algorithmus an einem Optimum angekommen ist. Außerdem kann es auch vorkommen, dass Modelle auch nach hunderten Iterationen schlichtweg nicht konvergieren.
Im gleichen Zuge wird klar, dass man diesen Iterationsprozess natürlich möglichst optimieren will um Zeit und Rechenleistung zu sparen. So gibt es beispielsweise iterative Algorithmen wie:
- Newton-Raphson-Verfahren
- IRLS (Iteratively Reweighted Least Squares)
Im Folgenden sieht man Informationen über den Iterationsprozess bei unserem Modell von vorhin. Es gab 9 Iterationen. Das bedeutet auch, dass lange nicht alle Werte berechnet wurden, die die konkave Fläche aus der 3D-Abbildung oben darstellen. Stattdessen wurden nur 8 weitere Punkte berechnet, bevor der 9. Punkt - das Maximum; rot eingezeichnet - gefunden wurde.
# Informationen über den Fitting-Prozess
print("Informationen über den Fitting-Prozess:")
print(f"Anzahl Iterationen: {logit_result.mle_retvals['iterations']}")
print(f"Konvergenz erreicht: {logit_result.mle_retvals['converged']}")
print(f"Log-Likelihood: {logit_result.llf:.2f}")
print(f"AIC: {logit_result.aic:.2f}")Informationen über den Fitting-Prozess:
Anzahl Iterationen: 9
Konvergenz erreicht: True
Log-Likelihood: -51.03
AIC: 106.07Statistische Inferenz bei der logistischen Regression
Einordnung der folgenden Abschnitte
Die kommenden Abschnitte führen viele neue und komplexe statistische Konzepte ein. Es ist völlig normal und erwartet, dass nicht jedes Detail sofort vollständig verstanden wird - selbst in einem fortgeschrittenen Kurs wie diesem.
Ziel dieser Abschnitte: Zu zeigen, dass bei der logistischen Regression die gleichen statistischen Werkzeuge zur Verfügung stehen wie bei der linearen Regression (Signifikanztests, Konfidenzintervalle, Standardfehler, Modellgütemaße), aber dass sie auf völlig anderen mathematischen Grundlagen basieren.
Was man mitnehmen sollte: Ein grundlegendes Verständnis, dass diese Methoden existieren und verfügbar sind. Die detaillierten mathematischen Herleitungen sind nicht prüfungsrelevant, sondern dienen dem vollständigen Bild der Methode.
Man sollte die Abschnitte also einmal aufmerksam durchlesen, aber machen sich keinen Stress machen, wenn nicht alles auf Anhieb klar ist. Die Hauptbotschaft ist: “Es gibt diese Tools prinzipiell auch hier, aber sie funktionieren anders.”
Statistische Signifikanz: Der Wald-Test
Jetzt, da wir verstehen wie MLE funktioniert, können wir auch verstehen woher die p-Werte in der logistischen Regression kommen! Bei der linearen Regression hatten wir die t-Verteilung, weil die Residuen normalverteilt waren. Aber bei der logistischen Regression haben wir binäre Daten (0 oder 1) - hier kann nichts normalverteilt sein!
# P-Werte und Signifikanz
print("Statistische Signifikanz:")
print(f"Körpergewicht p-Wert: {logit_result.pvalues['body_mass_g']:.2e}")
print(f"Körpergewicht z-Wert: {logit_result.tvalues['body_mass_g']:.2f}")
print(f"Standardfehler: {logit_result.bse['body_mass_g']:.6f}")Statistische Signifikanz:
Körpergewicht p-Wert: 7.99e-13
Körpergewicht z-Wert: 7.16
Standardfehler: 0.000870Der Trick liegt in der asymptotischen Normalverteilung der Maximum-Likelihood-Schätzer. Das ist ein fundamentales Ergebnis der Statistik:
Für große Stichproben sind Maximum-Likelihood-Schätzer annähernd normalverteilt: \[\hat{\beta}_j \sim N(\beta_j, \text{SE}(\hat{\beta}_j)^2)\]
Daraus folgt, dass die z-Statistik (nicht t-Statistik!) standard-normalverteilt ist: \[z = \frac{\hat{\beta}_j}{\text{SE}(\hat{\beta}_j)} \sim N(0,1)\]
Dies ist der Wald-Test für die Hypothese \(H_0: \beta_j = 0\).
Rechnen wir das konkret nach:
Wir haben β₁ = 0.006229 und SE(β₁) = 0.000870, also:
\[z = \frac{0.006229}{0.000870} = 7.16\]
# Wald-Test manuell nachrechnen
beta1_hat = logit_result.params['body_mass_g']
se_beta1 = logit_result.bse['body_mass_g']
z_score = beta1_hat / se_beta1
print("Wald-Test Schritt für Schritt:")
print(f"β₁ = {beta1_hat:.6f}")
print(f"SE(β₁) = {se_beta1:.6f}")
print(f"z = β₁/SE(β₁) = {beta1_hat:.6f}/{se_beta1:.6f} = {z_score:.2f}")
# P-Wert aus Standardnormalverteilung
from scipy import stats
p_value_manual = 2 * (1 - stats.norm.cdf(abs(z_score)))
print(f"\nP-Wert (zweiseitig): {p_value_manual:.2e}")
print(f"P-Wert (statsmodels): {logit_result.pvalues['body_mass_g']:.2e}")
print(f"\nInterpretation: z = {z_score:.2f} ist extrem hoch!")
print(f"Ein z-Wert > 2 entspricht schon p < 0.05")
print(f"Ein z-Wert von {z_score:.2f} entspricht p = {p_value_manual:.2e} (praktisch null)")Wald-Test Schritt für Schritt:
β₁ = 0.006229
SE(β₁) = 0.000870
z = β₁/SE(β₁) = 0.006229/0.000870 = 7.16
P-Wert (zweiseitig): 7.99e-13
P-Wert (statsmodels): 7.99e-13
Interpretation: z = 7.16 ist extrem hoch!
Ein z-Wert > 2 entspricht schon p < 0.05
Ein z-Wert von 7.16 entspricht p = 7.99e-13 (praktisch null)Die Übereinstimmung ist perfekt! Der extrem kleine p-Wert zeigt uns, dass der Zusammenhang zwischen Körpergewicht und Wahrscheinlichkeit der Artzugehörigkeit statistisch höchst signifikant ist.
Konfidenzintervalle
Die Konfidenzintervalle basieren ebenfalls auf der asymptotischen Normalverteilung. Ein 95%-Konfidenzintervall für β₁ berechnet sich als:
\[\text{KI} = \hat{\beta}_1 \pm 1.96 \times \text{SE}(\hat{\beta}_1)\]
Konkret gerechnet:
# Konfidenzintervalle manuell berechnen
beta1_hat = logit_result.params['body_mass_g']
se_beta1 = logit_result.bse['body_mass_g']
# 95%-KI für β₁
ki_lower = beta1_hat - 1.96 * se_beta1
ki_upper = beta1_hat + 1.96 * se_beta1
print("95%-Konfidenzintervall für β₁:")
print(f"Untere Grenze: {beta1_hat:.6f} - 1.96 × {se_beta1:.6f} = {ki_lower:.6f}")
print(f"Obere Grenze: {beta1_hat:.6f} + 1.96 × {se_beta1:.6f} = {ki_upper:.6f}")
print(f"KI: [{ki_lower:.6f}, {ki_upper:.6f}]")
# Vergleich mit statsmodels
print("\nVergleich mit statsmodels:")
print("Koeffizienten (Logit-Skala):")
print(logit_result.conf_int())
print("\nOdds Ratios:")
print(np.exp(logit_result.conf_int()))95%-Konfidenzintervall für β₁:
Untere Grenze: 0.006229 - 1.96 × 0.000870 = 0.004524
Obere Grenze: 0.006229 + 1.96 × 0.000870 = 0.007934
KI: [0.004524, 0.007934]
Vergleich mit statsmodels:
Koeffizienten (Logit-Skala):
0 1
Intercept -35.017463 -19.946386
body_mass_g 0.004524 0.007934
Odds Ratios:
0 1
Intercept 6.195963e-16 2.174677e-09
body_mass_g 1.004535e+00 1.007966e+00Interpretation: Das Konfidenzintervall für das Odds Ratio des Körpergewichts liegt zwischen 1.0045 und 1.0080. Da es nicht die 1 enthält, ist der Effekt signifikant - was mit unserem sehr kleinen p-Wert übereinstimmt.
Standardfehler aus der Fisher-Information
Ein letztes wichtiges Detail: Woher kommen die Standardfehler? Sie stammen aus der Fisher-Information-Matrix, die die zweiten Ableitungen der Log-Likelihood-Funktion enthält. Das ist deutlich komplexer als bei der linearen Regression, wo die Standardfehler direkt aus den Residuen berechnet werden können.
# Fisher-Information und Kovarianzmatrix
print("Kovarianzmatrix der Parameter:")
print(logit_result.cov_params())
print()
print("Standardfehler (Diagonal der Kovarianzmatrix):")
print(f"SE(β₀): {np.sqrt(logit_result.cov_params().iloc[0,0]):.6f}")
print(f"SE(β₁): {np.sqrt(logit_result.cov_params().iloc[1,1]):.6f}")
print()
print("Vergleich mit direkter Ausgabe:")
print(logit_result.bse)Kovarianzmatrix der Parameter:
Intercept body_mass_g
Intercept 14.781974 -3.336995e-03
body_mass_g -0.003337 7.566266e-07
Standardfehler (Diagonal der Kovarianzmatrix):
SE(β₀): 3.844733
SE(β₁): 0.000870
Vergleich mit direkter Ausgabe:
Intercept 3.844733
body_mass_g 0.000870
dtype: float64Likelihood-Ratio-Test: Eine Alternative zum Wald-Test
Neben dem Wald-Test gibt es noch einen anderen wichtigen statistischen Test in der logistischen Regression: den Likelihood-Ratio-Test (LRT). Dieser vergleicht das vollständige Modell mit einem reduzierten Modell (z.B. nur Intercept).
Die Idee: Wenn das Körpergewicht keinen Effekt hätte (β₁ = 0), wäre ein Modell nur mit Intercept genauso gut. Aber ist das wirklich so?
# Null-Modell (nur Intercept) anpassen
null_model = smf.logit('species_binary ~ 1', data=penguins_binary).fit()
print("Likelihood-Ratio-Test Schritt für Schritt:")
print(f"Vollständiges Modell Log-Likelihood: {logit_result.llf:.2f}")
print(f"Null-Modell Log-Likelihood: {null_model.llf:.2f}")
print(f"Unterschied: {logit_result.llf - null_model.llf:.2f}")
# LR-Statistik berechnen
lr_statistic = 2 * (logit_result.llf - null_model.llf)
print(f"LR-Statistik: 2 × {logit_result.llf - null_model.llf:.2f} = {lr_statistic:.2f}")
# P-Wert aus Chi²-Verteilung
df = 1 # Ein Parameter-Unterschied
p_value_lr = 1 - stats.chi2.cdf(lr_statistic, df)
print(f"P-Wert (Chi²-Verteilung, df=1): {p_value_lr:.2e}")
print(f"\nInterpretation: LR = {lr_statistic:.2f} ist extrem hoch!")
print(f"Das Körpergewicht verbessert das Modell dramatisch!")Optimization terminated successfully.
Current function value: 0.687917
Iterations 4
Likelihood-Ratio-Test Schritt für Schritt:
Vollständiges Modell Log-Likelihood: -51.03
Null-Modell Log-Likelihood: -188.49
Unterschied: 137.46
LR-Statistik: 2 × 137.46 = 274.91
P-Wert (Chi²-Verteilung, df=1): 0.00e+00
Interpretation: LR = 274.91 ist extrem hoch!
Das Körpergewicht verbessert das Modell dramatisch!Der LRT ist oft robuster als der Wald-Test, besonders bei kleineren Stichproben oder extremen Koeffizienten.
Modellgüte: McFadden’s Pseudo-R2
Bei der linearen Regression hatten wir R² als Maß für die Modellgüte. Bei der logistischen Regression gibt es verschiedene Pseudo-R²-Maße. Das gebräuchlichste ist McFadden’s Pseudo-R²:
\[R^2_{\text{McFadden}} = 1 - \frac{\ell(\text{vollständiges Modell})}{\ell(\text{Null-Modell})}\]
Konkret berechnet:
# McFadden's Pseudo-R² berechnen
mcfadden_r2 = 1 - (logit_result.llf / null_model.llf)
print("McFadden's Pseudo-R² Schritt für Schritt:")
print(f"Vollständiges Modell LL: {logit_result.llf:.2f}")
print(f"Null-Modell LL: {null_model.llf:.2f}")
print(f"Verhältnis: {logit_result.llf:.2f} / {null_model.llf:.2f} = {logit_result.llf / null_model.llf:.4f}")
print(f"Pseudo-R²: 1 - {logit_result.llf / null_model.llf:.4f} = {mcfadden_r2:.4f}")
print(f"\nInterpretation: Das Modell erklärt {mcfadden_r2*100:.1f}% der 'Deviance'")
# Aus statsmodels direkt
print(f"Statsmodels Pseudo-R²: {logit_result.prsquared:.4f}")
print(f"\nBewertung: Ein Pseudo-R² von {mcfadden_r2:.3f} ist sehr hoch!")McFadden's Pseudo-R² Schritt für Schritt:
Vollständiges Modell LL: -51.03
Null-Modell LL: -188.49
Verhältnis: -51.03 / -188.49 = 0.2708
Pseudo-R²: 1 - 0.2708 = 0.7292
Interpretation: Das Modell erklärt 72.9% der 'Deviance'
Statsmodels Pseudo-R²: 0.7292
Bewertung: Ein Pseudo-R² von 0.729 ist sehr hoch!Übungen
Übung 1
Was bedeutet ein Odds Ratio von 2.5?
Wähle die korrekte Interpretation:Übung 2
Trainiere zwei logistische Regressionsmodelle mit dem Palmer Penguins Datensatz - genau wie das Modell oben im Kapitel, nur mit den beiden anderen Art-Paaren:
- Modell 1: Adelie vs. Chinstrap (basierend auf Körpergewicht) - mit sklearn
- Modell 2: Gentoo vs. Chinstrap (basierend auf Körpergewicht) - mit statsmodels
Visualisiere beide Modelle nebeneinander in einer Figure mit zwei Axes und mache Vorhersagen für die Körpergewichte 3500g, 4500g und 5500g.