import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
import statsmodels.api as sm
from scipy.stats import chi2
from sklearn.metrics import confusion_matrix, classification_report, roc_curve, auc
np.random.seed(42)Klassifikationsleistung bewerten
Im vorherigen Kapitel haben wir die logistische Regression kennengelernt und damit die Wahrscheinlichkeit modelliert, dass ein Pinguin zur Art Gentoo gehört, basierend auf seinem Körpergewicht. Das war jedoch die einfachstmögliche logistische Regression mit nur einer numerischen x-Variable.
Genauso wie bei unseren linearen Modellen können wir auch bei der logistischen Regression mehrere Effekte ins Modell aufnehmen. Als Beispiel erweitern wir unser Pinguin-Modell um eine kategorielle Variable: das Geschlecht. Wir werden also zwei Modelle vergleichen:
-
Modell 1:
species_binary ~ body_mass_g(wie in Kapitel 5.1) -
Modell 2:
species_binary ~ body_mass_g + C(sex)(neu)
# Palmer Penguins Datensatz laden und vorbereiten
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Farbschema
colors = {'Adelie': '#FF8C00', 'Gentoo': '#159090'}
# Daten für Adelie und Gentoo vorbereiten
penguins_binary = penguins[penguins['species'].isin(['Adelie', 'Gentoo'])].copy()
penguins_binary = penguins_binary.dropna(subset=['body_mass_g', 'sex'])
# Binäre Kodierung: Adelie = 0, Gentoo = 1
penguins_binary['species_binary'] = penguins_binary['species'].map({'Adelie': 0, 'Gentoo': 1})
Modelle anpassen
Modell 1
Beginnen wir dort, wo wir im letzten Kapitel aufgehört haben, mit demselben Datensatz und denselben beiden Arten.
# Modell 1: Nur Körpergewicht (wie in Kapitel 5.1)
model1 = smf.logit('species_binary ~ body_mass_g', data=penguins_binary)
result1 = model1.fit()
print(result1.summary())Optimization terminated successfully.
Current function value: 0.181899
Iterations 9
Logit Regression Results
==============================================================================
Dep. Variable: species_binary No. Observations: 265
Model: Logit Df Residuals: 263
Method: MLE Df Model: 1
Date: Di, 19 Aug 2025 Pseudo R-squ.: 0.7356
Time: 11:46:01 Log-Likelihood: -48.203
converged: True LL-Null: -182.31
Covariance Type: nonrobust LLR p-value: 2.793e-60
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
Intercept -27.9475 4.028 -6.938 0.000 -35.842 -20.053
body_mass_g 0.0063 0.001 6.950 0.000 0.005 0.008
===============================================================================Code zeigen/verstecken
# Modell 1 visualisieren (wie in Kapitel 5.1)
fig, ax = plt.subplots(figsize=(9, 5), layout='tight')
# Originaldaten
adelie_data = penguins_binary[penguins_binary['species'] == 'Adelie']
gentoo_data = penguins_binary[penguins_binary['species'] == 'Gentoo']
ax.scatter(adelie_data['body_mass_g'], adelie_data['species_binary'],
alpha=0.6, color=colors['Adelie'], label='Adelie', s=50)
ax.scatter(gentoo_data['body_mass_g'], gentoo_data['species_binary'],
alpha=0.6, color=colors['Gentoo'], label='Gentoo', s=50)
# Logistische Kurve
x_range = np.linspace(penguins_binary['body_mass_g'].min(),
penguins_binary['body_mass_g'].max(), 200)
predictions = result1.predict(pd.DataFrame({'body_mass_g': x_range}))
ax.plot(x_range, predictions, 'red', linewidth=3, label='Logistische Regression')
ax.axhline(y=0.5, color='gray', linestyle='--', alpha=0.7, label='50%-Marke')
ax.set_xlabel('Körpergewicht (g)')
ax.set_ylabel('Wahrscheinlichkeit P(Gentoo)')
ax.set_title('Modell 1: Nur Körpergewicht')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()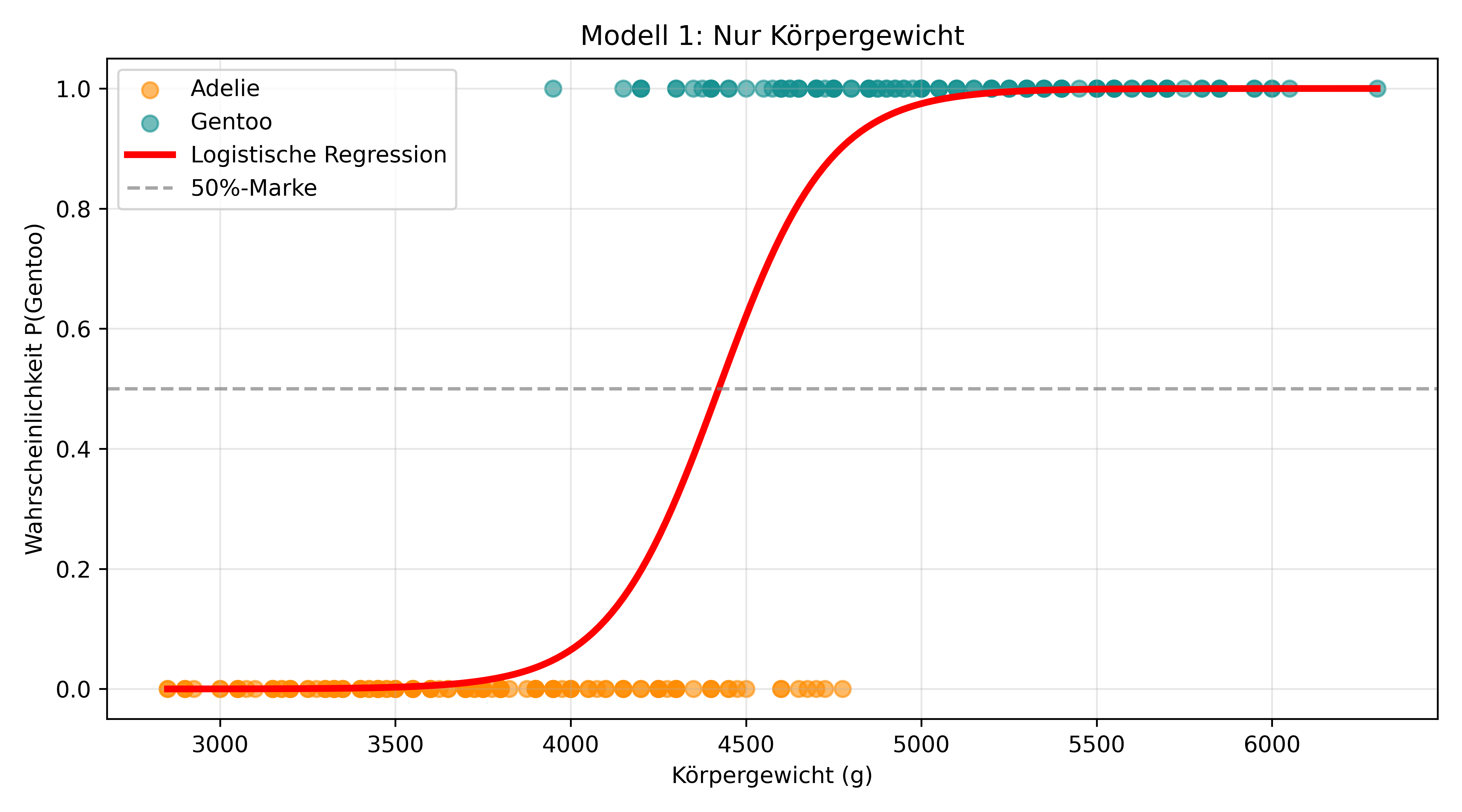
Modell 2
Nun wollen wir das Geschlecht als zusätzlichen Faktor einbeziehen. Um dies zu visualisieren, können wir die Punkte durch unterschiedliche Symbole darstellen - allerdings würden wir bei so vielen Punkten die Symbolformen kaum wahrnehmen. Deshalb wenden wir einen kleinen Visualisierungs-Trick an: Wir verschieben männliche und weibliche Punkte leicht auf der y-Achse, damit die Symbole nicht überlappen. Natürlich liegen alle Punkte eigentlich nur exakt auf 0 oder 1, aber diese Darstellung bringt einen klaren Mehrwert für das Verständnis. Das gleiche gilt dann auch für die jeweilige Kurve.
# Modell 2: Körpergewicht + Geschlecht
model2 = smf.logit('species_binary ~ body_mass_g + C(sex)', data=penguins_binary)
result2 = model2.fit()Optimization terminated successfully.
Current function value: 0.010528
Iterations 16Code zeigen/verstecken
# Erweiterte Visualisierung mit Geschlecht
fig, ax = plt.subplots(figsize=(9, 5), layout='tight')
# Leichter Versatz für bessere Sichtbarkeit
offset = 0.01
# Datenpunkte mit verschiedenen Symbolen und leichtem Versatz
for species in ['Adelie', 'Gentoo']:
for sex in ['male', 'female']:
data_subset = penguins_binary[
(penguins_binary['species'] == species) &
(penguins_binary['sex'] == sex)
]
if len(data_subset) > 0:
# Leichter Versatz je nach Geschlecht
y_values = data_subset['species_binary'].copy()
if sex == 'male':
y_values = y_values + offset
else:
y_values = y_values - offset
# Symbol je nach Geschlecht
marker = 'o' if sex == 'male' else '^'
ax.scatter(data_subset['body_mass_g'], y_values,
alpha=0.6, color=colors[species],
marker=marker, s=50,
label=f'{species} {sex}')
# Separate Kurven für männlich und weiblich mit Versatz
x_range = np.linspace(penguins_binary['body_mass_g'].min(),
penguins_binary['body_mass_g'].max(), 200)
for sex in ['male', 'female']:
pred_data = pd.DataFrame({'body_mass_g': x_range, 'sex': sex})
predictions = result2.predict(pred_data)
# Versatz für die Kurven
if sex == 'male':
predictions += offset
else:
predictions -= offset
linestyle = '--' if sex == 'male' else ':'
ax.plot(x_range, predictions, 'red', linewidth=3,
linestyle=linestyle, label=f'Vorhersage {sex}')
ax.axhline(y=0.5, color='gray', linestyle=':', alpha=0.7)
ax.set_xlabel('Körpergewicht (g)')
ax.set_ylabel('Wahrscheinlichkeit P(Gentoo)')
ax.set_title('Modell 2: Körpergewicht + Geschlecht')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()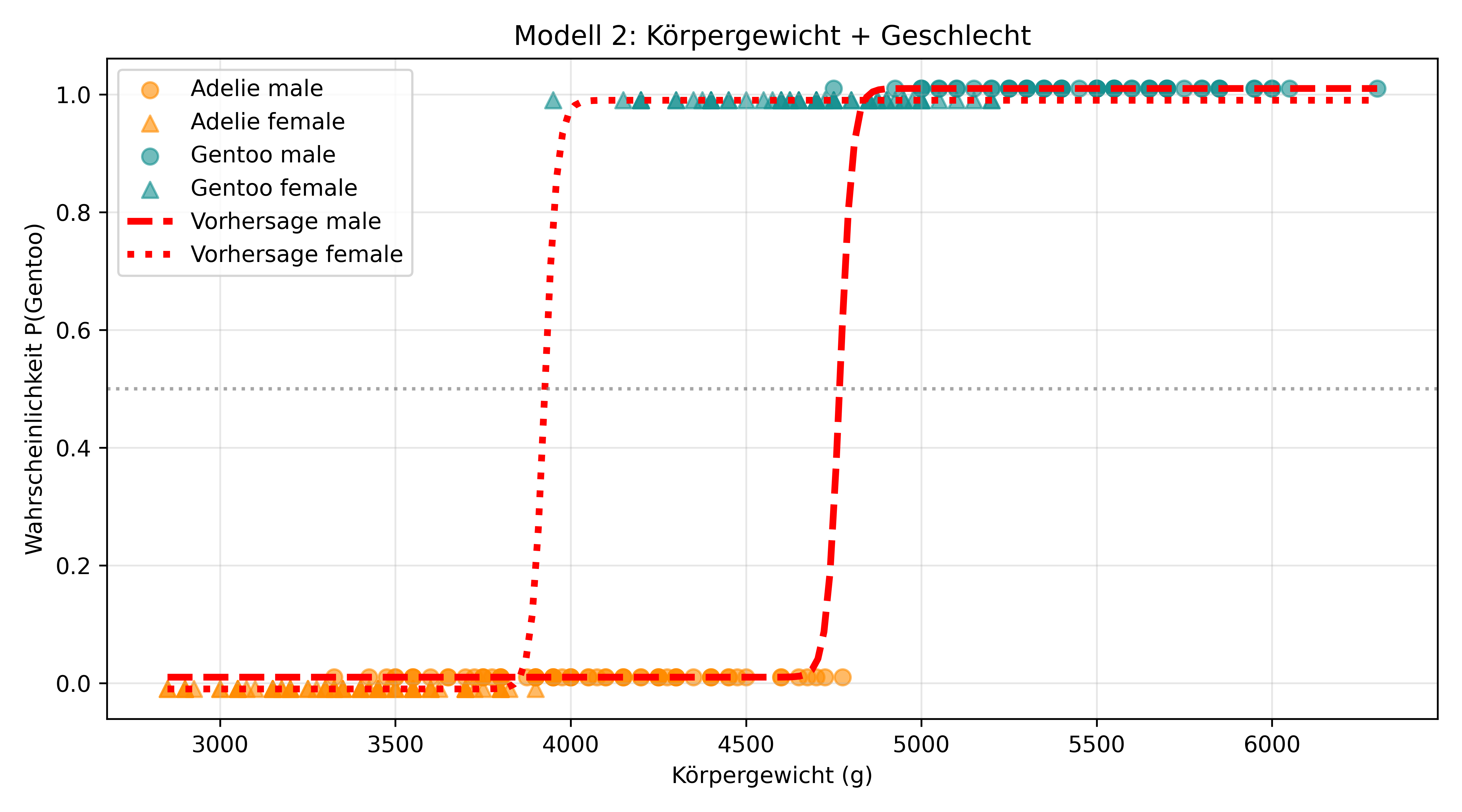
In der Abbildung sehen wir die zwei parallelen Sigmoid-Kurven: eine gestrichelte Linie für männliche Pinguine und eine gepunktete für weibliche. Diese Verschiebung der Kurven zeigt den Effekt des Geschlechts.
Interpretation des Geschlechts-Effekts
Schauen wir uns die Koeffizienten systematisch an. Der Koeffizient C(sex)[T.male] zeigt den Effekt des männlichen Geschlechts, wobei die Dummy-Codierung “female” als Referenzkategorie verwendet.
# Modell-Zusammenfassung anzeigen
print(result2.summary()) Logit Regression Results
==============================================================================
Dep. Variable: species_binary No. Observations: 265
Model: Logit Df Residuals: 262
Method: MLE Df Model: 2
Date: Di, 19 Aug 2025 Pseudo R-squ.: 0.9847
Time: 11:46:02 Log-Likelihood: -2.7899
converged: True LL-Null: -182.31
Covariance Type: nonrobust LLR p-value: 1.089e-78
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
Intercept -216.1125 158.246 -1.366 0.172 -526.270 94.045
C(sex)[T.male] -46.3532 33.610 -1.379 0.168 -112.227 19.521
body_mass_g 0.0551 0.040 1.365 0.172 -0.024 0.134
==================================================================================
Possibly complete quasi-separation: A fraction 0.95 of observations can be
perfectly predicted. This might indicate that there is complete
quasi-separation. In this case some parameters will not be identified.Genau wie bei linearen Modellen wird für die Referenzgruppe (weiblich) 0 addiert, für die andere Gruppe (männlich) wird der geschätzte Koeffizient addiert. Das passiert auf der Logit-Skala:
- Weiblicher Pinguin: Logit = β₀ + β₁ × Körpergewicht + 0
- Männlicher Pinguin: Logit = β₀ + β₁ × Körpergewicht + β₂
# Koeffizienten extrahieren
beta0 = result2.params['Intercept']
beta1 = result2.params['body_mass_g']
beta2 = result2.params['C(sex)[T.male]']
print("Koeffizienten des erweiterten Modells:")
print(f"β₀ (Intercept): {beta0:.4f}")
print(f"β₁ (Körpergewicht): {beta1:.6f}")
print(f"β₂ (männlich): {beta2:.4f}")Koeffizienten des erweiterten Modells:
β₀ (Intercept): -216.1125
β₁ (Körpergewicht): 0.055054
β₂ (männlich): -46.3532Konkrete Beispielrechnung
Betrachten wir zwei Pinguine mit identischem Körpergewicht (4500g), aber unterschiedlichem Geschlecht:
# Beispielrechnung für 4500g Pinguine
mass_example = 4500
# Weiblicher Pinguin
logit_female = beta0 + beta1 * mass_example + 0 # + 0 für Referenzgruppe
prob_female = 1 / (1 + np.exp(-logit_female))
# Männlicher Pinguin
logit_male = beta0 + beta1 * mass_example + beta2 # + β₂ für männlich
prob_male = 1 / (1 + np.exp(-logit_male))
print(f"4500g Pinguin - Geschlechtsvergleich:")
print(f"Weiblich: Logit = {logit_female:.4f} → P(Gentoo) = {prob_female:.4f} ({prob_female*100:.1f}%)")
print(f"Männlich: Logit = {logit_male:.4f} → P(Gentoo) = {prob_male:.4f} ({prob_male*100:.1f}%)")
print(f"Differenz: {logit_male - logit_female:.4f} (entspricht genau β₂)")4500g Pinguin - Geschlechtsvergleich:
Weiblich: Logit = 31.6311 → P(Gentoo) = 1.0000 (100.0%)
Männlich: Logit = -14.7220 → P(Gentoo) = 0.0000 (0.0%)
Differenz: -46.3532 (entspricht genau β₂)Der Koeffizient β₂ ist genau die konstante Verschiebung zwischen den beiden Kurven auf der Logit-Skala. Diese Verschiebung ist über alle Körpergewichte hinweg gleich, was zu den parallelen Sigmoid-Kurven führt, die wir in der Abbildung sehen.
# Verschiebung für verschiedene Gewichte demonstrieren
test_weights = [4000, 4500, 5000]
print("Konstante Logit-Verschiebung über alle Gewichte:")
for weight in test_weights:
logit_f = beta0 + beta1 * weight + 0
logit_m = beta0 + beta1 * weight + beta2
difference = logit_m - logit_f
print(f"{weight}g: Differenz = {difference:.4f}")Konstante Logit-Verschiebung über alle Gewichte:
4000g: Differenz = -46.3532
4500g: Differenz = -46.3532
5000g: Differenz = -46.3532Schließlich hier mal wieder ein Beispiel von desmos.com, bei dem wir den prinzipiellen Einfluß unserer Variablen - wenn auch mit ganz anderen Werten - auf die Kurve sehen können:
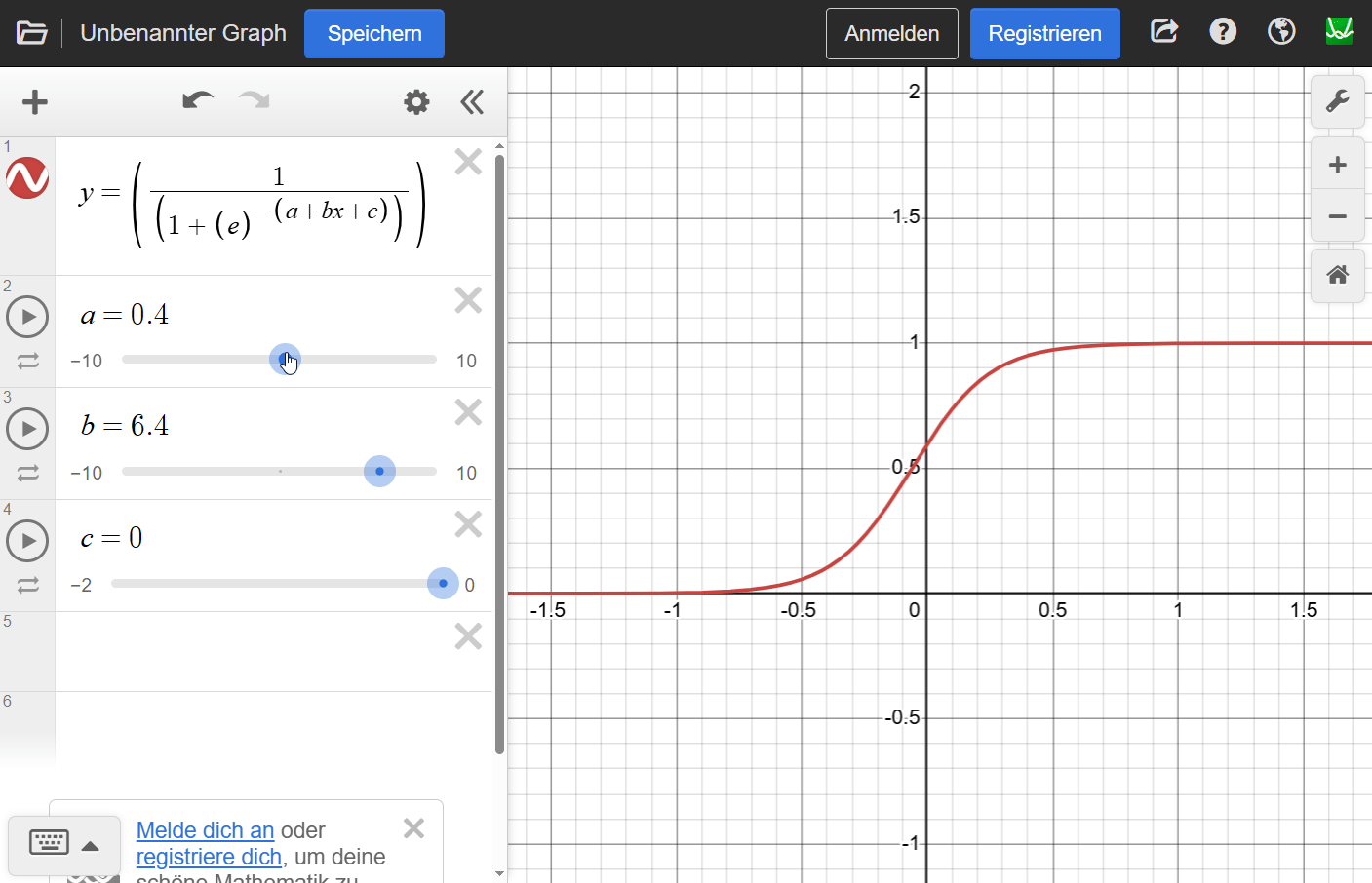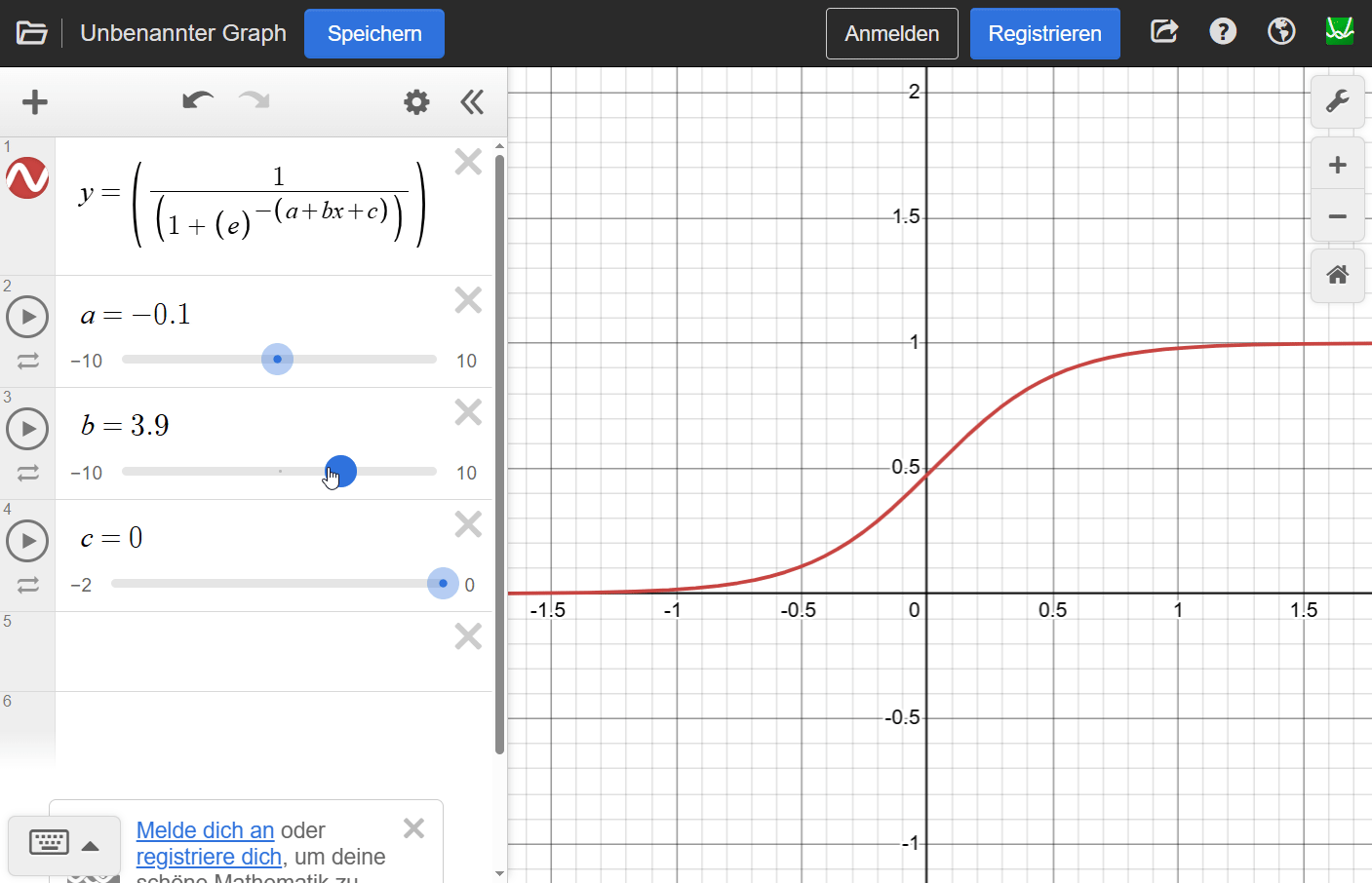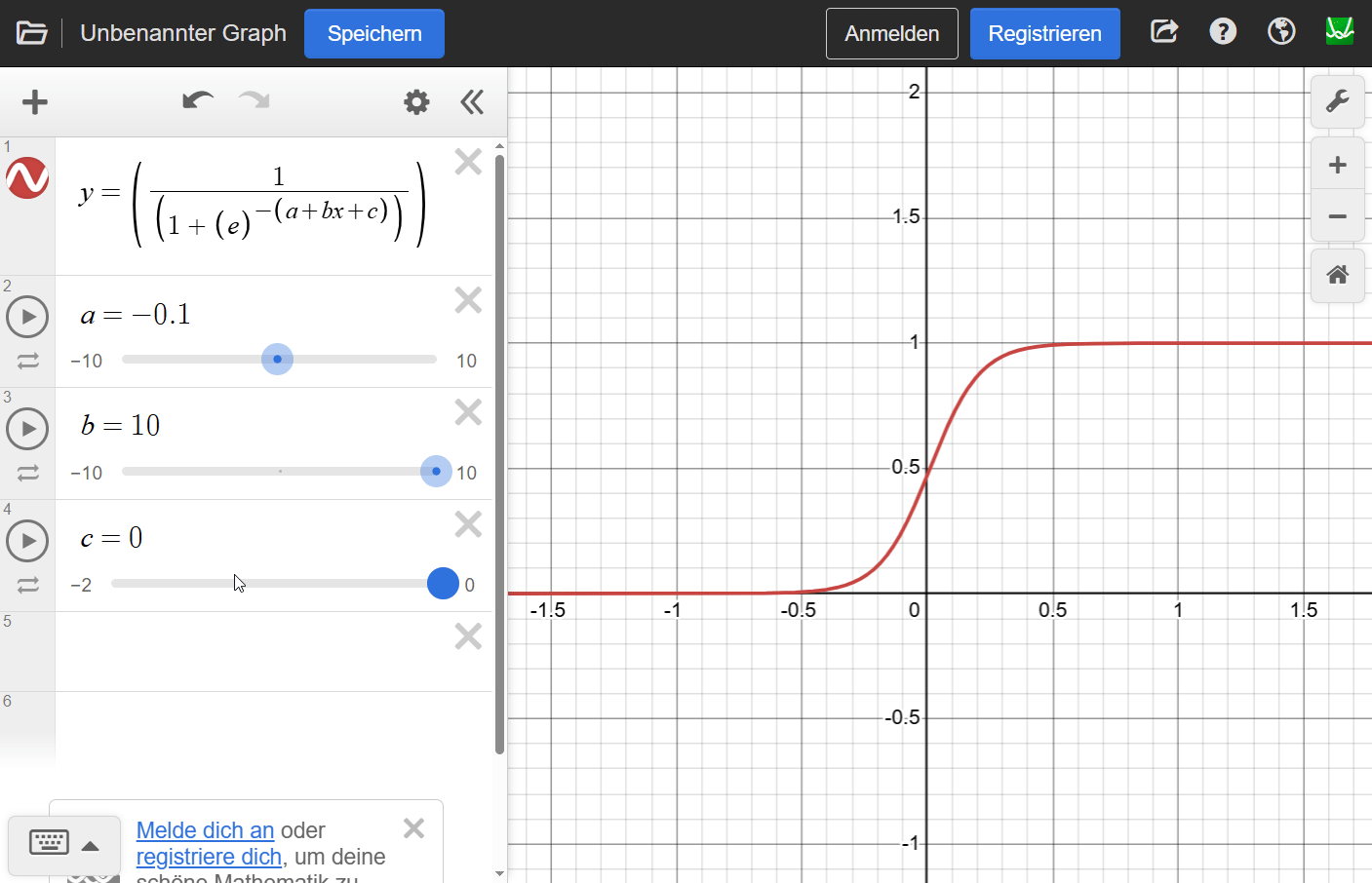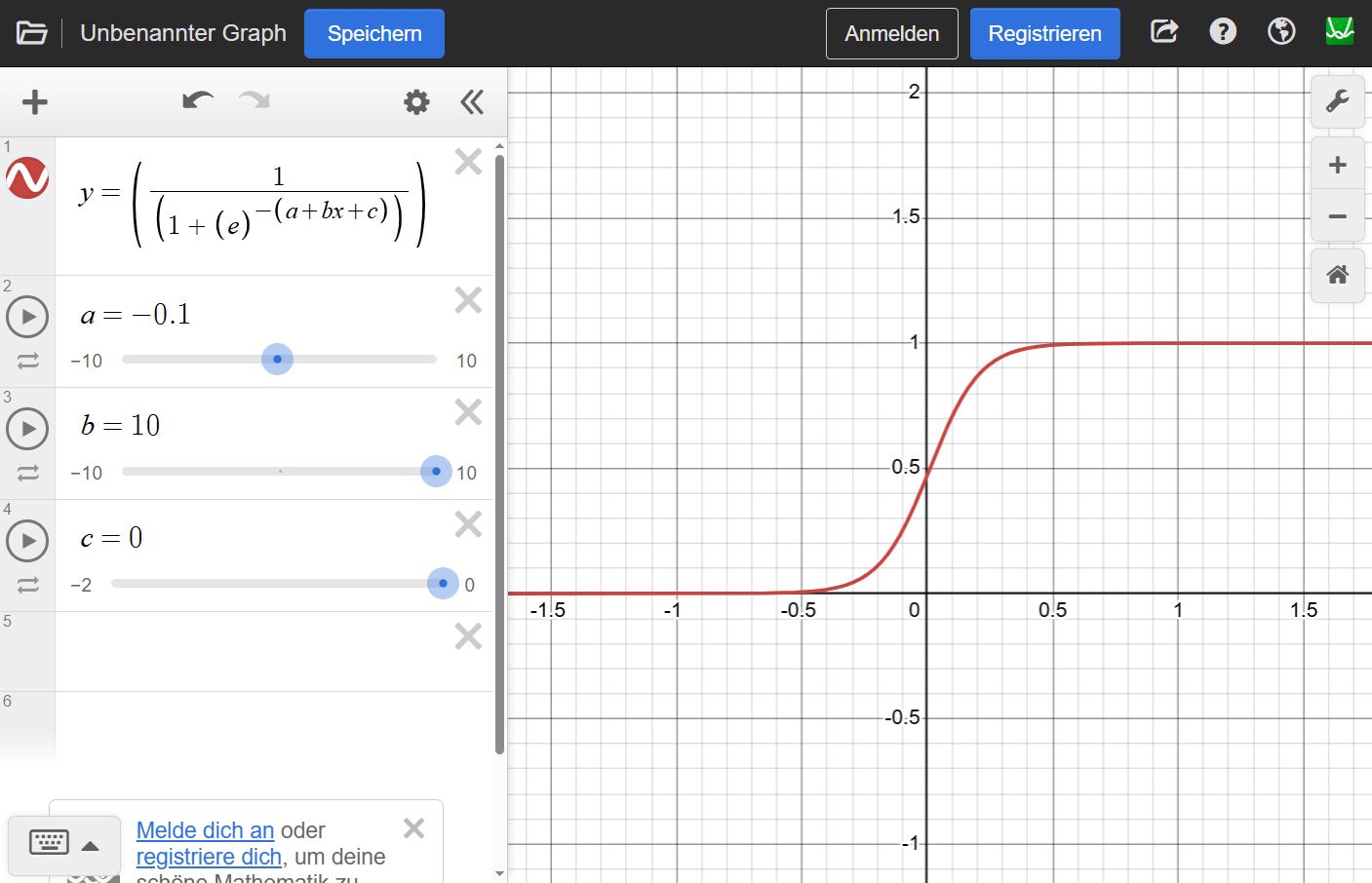
Warnung: Ein “zu gutes” Modell?
Bei Modell 2 erhalten wir eine Warnung: “Possibly complete quasi-separation”. Das ist ein potenzielles Problem, das darauf hinweist, dass unser Modell die Daten fast perfekt trennen kann. Dies passiert hier, weil die Kombination aus Körpergewicht und Geschlecht eine nahezu perfekte Vorhersage der Pinguinart ermöglicht - es gibt kaum noch Überlappungsbereiche zwischen den Gruppen.
# Detailanalyse der Datenverteilung
print("Gewichtsverteilung nach Art und Geschlecht:")
weight_analysis = penguins_binary.groupby(['species', 'sex'])['body_mass_g'].agg(['min', 'max', 'mean']).round(0)
print(weight_analysis)Gewichtsverteilung nach Art und Geschlecht:
min max mean
species sex
Adelie female 2850.0 3900.0 3369.0
male 3325.0 4775.0 4043.0
Gentoo female 3950.0 5200.0 4680.0
male 4750.0 6300.0 5485.0Die biologische Erklärung: Sexualdimorphismus (Größenunterschiede zwischen Männchen und Weibchen) kombiniert mit Artunterschieden führt dazu, dass die vier Gruppen (Adelie ♂/♀, Gentoo ♂/♀) sehr unterschiedliche Gewichtsbereiche haben.
Modellvergleich
Welches Modell ist objektiv besser? Betrachten wir verschiedene uns bekannte Bewertungsmetriken:
# Modellvergleich: Statistische Maße
print("MODELLVERGLEICH")
print("=" * 50)
print(f"Modell 1 - Log-Likelihood: {result1.llf:.3f}")
print(f"Modell 1 - AIC: {result1.aic:.3f}")
print(f"Modell 1 - BIC: {result1.bic:.3f}")
print(f"Modell 1 - Pseudo R²: {result1.prsquared:.3f}")
print(f"\nModell 2 - Log-Likelihood: {result2.llf:.3f}")
print(f"Modell 2 - AIC: {result2.aic:.3f}")
print(f"Modell 2 - BIC: {result2.bic:.3f}")
print(f"Modell 2 - Pseudo R²: {result2.prsquared:.3f}")
# Likelihood-Ratio-Test
lr_stat = 2 * (result2.llf - result1.llf)
df_diff = result2.df_model - result1.df_model
p_value = 1 - chi2.cdf(lr_stat, df_diff)
print(f"\nLikelihood-Ratio-Test:")
print(f"LR-Statistik: {lr_stat:.3f}")
print(f"p-Wert: {p_value:.3f}")MODELLVERGLEICH
==================================================
Modell 1 - Log-Likelihood: -48.203
Modell 1 - AIC: 100.407
Modell 1 - BIC: 107.566
Modell 1 - Pseudo R²: 0.736
Modell 2 - Log-Likelihood: -2.790
Modell 2 - AIC: 11.580
Modell 2 - BIC: 22.319
Modell 2 - Pseudo R²: 0.985
Likelihood-Ratio-Test:
LR-Statistik: 90.827
p-Wert: 0.000Alle statistischen Maße sprechen klar für Modell 2: deutlich höheres Pseudo-R², niedrigere AIC/BIC-Werte und ein hochsignifikanter Likelihood-Ratio-Test1.
Klassifikationsleistung bewerten
Während statistische Maße wie AIC und Pseudo-R² die Modellgüte aus wahrscheinlichkeitstheoretischer Sicht bewerten, ist in Machine Learning-Anwendungen oft die Klassifikationsleistung entscheidend. Hier transformieren wir die Wahrscheinlichkeitsschätzungen in konkrete Entscheidungen und bewerten, wie gut unsere Modelle bei der tatsächlichen Klassifikation abschneiden.
Der Übergang von Wahrscheinlichkeiten zu Klassifikationen erfolgt wie gesagt durch einen Schwellenwert (meist 0.5): Wahrscheinlichkeiten ≥ 0.5 werden als “Gentoo” klassifiziert, Werte < 0.5 als “Adelie”. Diese scheinbar simple Entscheidung hat weitreichende Konsequenzen für die Bewertung der Modellleistung.
Schauen wir also mal wie oft unser Modell die Arten korrekt klassifiziert.
# Vorhersagen für beide Modelle
prob1 = result1.predict(penguins_binary)
prob2 = result2.predict(penguins_binary)
# Binäre Klassifikationen (Schwellenwert 0.5)
pred1 = (prob1 >= 0.5).astype(int)
pred2 = (prob2 >= 0.5).astype(int)
# Wahre Werte
y_true = penguins_binary['species_binary']Wir können auch hier mal eine Versuch starten zu visualisieren welche Punkte genau laut unseren Modellen falsch klassifiziert wurden. In der folgenden Abbildung sind all die Punkte, die laut Modell genau der falschen Art zugeordnet wurden, zusätzlich auf der Kurve eingezeichnet und mit einer vertikalen Linie mit dem eigentlichen Punkt verbunden:
Code zeigen/verstecken
# Visualisierung der falsch klassifizierten Punkte
fig, axes = plt.subplots(1, 2, figsize=(15, 6), layout='tight')
# Leichter Versatz für bessere Sichtbarkeit
offset = 0.01
# SUBPLOT 1: Modell 1
ax = axes[0]
# Falsch klassifizierte Punkte - vertikale Linien zuerst (hinter allem)
wrong_indices = pred1 != y_true
wrong_data = penguins_binary[wrong_indices]
if len(wrong_data) > 0:
for _, row in wrong_data.iterrows():
pred_val = result1.predict(pd.DataFrame({'body_mass_g': [row['body_mass_g']]}))[0]
species_color = colors[row['species']]
# Vertikale Linie in der gleichen Farbe (hinter allem)
ax.plot([row['body_mass_g'], row['body_mass_g']],
[row['species_binary'], pred_val],
color=species_color, linewidth=2, alpha=0.8, zorder=1);
# Logistische Kurve
x_range = np.linspace(penguins_binary['body_mass_g'].min(),
penguins_binary['body_mass_g'].max(), 200)
predictions_curve = result1.predict(pd.DataFrame({'body_mass_g': x_range}));
ax.plot(x_range, predictions_curve, 'red', linewidth=3, zorder=3);
# Alle Datenpunkte (halbtransparent)
for species in ['Adelie', 'Gentoo']:
data_subset = penguins_binary[penguins_binary['species'] == species]
ax.scatter(data_subset['body_mass_g'], data_subset['species_binary'],
alpha=0.5, color=colors[species], s=50, zorder=2);
# Falsch klassifizierte Punkte auf der Kurve (über der roten Linie)
if len(wrong_data) > 0:
for _, row in wrong_data.iterrows():
pred_val = result1.predict(pd.DataFrame({'body_mass_g': [row['body_mass_g']]}))[0]
species_color = colors[row['species']]
# Punkt auf der Kurve in der richtigen Farbe
ax.scatter(row['body_mass_g'], pred_val,
color=species_color, s=50, alpha=0.5, zorder=4);
ax.axhline(y=0.5, color='gray', linestyle='--', alpha=0.7, zorder=2);
ax.set_xlabel('Körpergewicht (g)');
ax.set_ylabel('Wahrscheinlichkeit P(Gentoo)');
ax.set_title('Modell 1: Falsch klassifizierte Punkte');
ax.grid(True, alpha=0.3, zorder=0);
# SUBPLOT 2: Modell 2
ax = axes[1]
# Falsch klassifizierte Punkte - vertikale Linien zuerst (hinter allem)
wrong_indices2 = pred2 != y_true
wrong_data2 = penguins_binary[wrong_indices2]
if len(wrong_data2) > 0:
for _, row in wrong_data2.iterrows():
pred_val = result2.predict(pd.DataFrame({'body_mass_g': [row['body_mass_g']],
'sex': [row['sex']]}))[0]
species_color = colors[row['species']]
# Versatz für ursprünglichen Punkt
original_y = row['species_binary']
if row['sex'] == 'male':
original_y += offset
else:
original_y -= offset
# Versatz für Punkt auf der Kurve
curve_y = pred_val
if row['sex'] == 'male':
curve_y += offset
else:
curve_y -= offset
# Vertikale Linie in der gleichen Farbe (hinter allem)
ax.plot([row['body_mass_g'], row['body_mass_g']],
[original_y, curve_y],
color=species_color, linewidth=2, alpha=0.8, zorder=1);
# Vorhersagekurven mit Versatz
for sex in ['male', 'female']:
pred_data = pd.DataFrame({'body_mass_g': x_range, 'sex': sex})
predictions_curve = result2.predict(pred_data)
# Versatz für die Kurven
if sex == 'male':
predictions_curve += offset
else:
predictions_curve -= offset
linestyle = '--' if sex == 'male' else ':'
ax.plot(x_range, predictions_curve, 'red', linewidth=3,
linestyle=linestyle, zorder=3);
# Alle Datenpunkte mit Geschlechter-Symbolen und Versatz (halbtransparent)
for species in ['Adelie', 'Gentoo']:
for sex in ['male', 'female']:
data_subset = penguins_binary[
(penguins_binary['species'] == species) &
(penguins_binary['sex'] == sex)
]
if len(data_subset) > 0:
# Leichter Versatz je nach Geschlecht
y_values = data_subset['species_binary'].copy()
if sex == 'male':
y_values = y_values + offset
else:
y_values = y_values - offset
# Symbol je nach Geschlecht
marker = 'o' if sex == 'male' else '^'
ax.scatter(data_subset['body_mass_g'], y_values,
alpha=0.5, color=colors[species],
marker=marker, s=50, zorder=2);
# Falsch klassifizierte Punkte auf den Kurven (über den roten Linien)
if len(wrong_data2) > 0:
for _, row in wrong_data2.iterrows():
pred_val = result2.predict(pd.DataFrame({'body_mass_g': [row['body_mass_g']],
'sex': [row['sex']]}))[0]
species_color = colors[row['species']]
# Versatz für Punkt auf der Kurve
if row['sex'] == 'male':
pred_val += offset
else:
pred_val -= offset
# Punkt auf der entsprechenden Kurve in der richtigen Farbe
marker = 'o' if row['sex'] == 'male' else '^'
ax.scatter(row['body_mass_g'], pred_val,
color=species_color, s=50, marker=marker, alpha=0.5, zorder=4);
ax.axhline(y=0.5, color='gray', linestyle=':', alpha=0.7, zorder=2);
ax.set_xlabel('Körpergewicht (g)');
ax.set_ylabel('Wahrscheinlichkeit P(Gentoo)');
ax.set_title('Modell 2: Falsch klassifizierte Punkte');
ax.grid(True, alpha=0.3, zorder=0)
plt.show()
Confusion Matrix: Die Grundlage aller Klassifikationsmetriken
Wenn wir aber nun anfangen auszuzählen wie oft das Modell korrekt und falsch klassifiziert haben, dann sollten wir es auch gleich richtig machen - nämlich mit der Confusion Matrix. Die Confusion Matrix (Konfusionsmatrix) ist das Herzstück der Klassifikationsbewertung. Sie zeigt alle vier möglichen Kombinationen von tatsächlichen und vorhergesagten Klassen in einer 2×2-Tabelle. Jede Zelle hat eine spezifische Bedeutung:
- True Positives (TP): Korrekt als Gentoo klassifizierte Gentoo-Pinguine
-
True Negatives (TN): Korrekt als Adelie klassifizierte Adelie-Pinguine
- False Positives (FP): Fälschlicherweise als Gentoo klassifizierte Adelie-Pinguine
- False Negatives (FN): Fälschlicherweise als Adelie klassifizierte Gentoo-Pinguine
# Confusion Matrices
cm1 = confusion_matrix(y_true, pred1)
cm2 = confusion_matrix(y_true, pred2)
print("Confusion Matrix - Modell 1:")
print(" Vorhergesagt")
print(" Adelie Gentoo")
print(f"Tatsächlich")
print(f"Adelie {cm1[0,0]:6d} {cm1[0,1]:6d}")
print(f"Gentoo {cm1[1,0]:6d} {cm1[1,1]:6d}")
print("\nConfusion Matrix - Modell 2:")
print(" Vorhergesagt")
print(" Adelie Gentoo")
print(f"Tatsächlich")
print(f"Adelie {cm2[0,0]:6d} {cm2[0,1]:6d}")
print(f"Gentoo {cm2[1,0]:6d} {cm2[1,1]:6d}")Confusion Matrix - Modell 1:
Vorhergesagt
Adelie Gentoo
Tatsächlich
Adelie 135 11
Gentoo 13 106
Confusion Matrix - Modell 2:
Vorhergesagt
Adelie Gentoo
Tatsächlich
Adelie 145 1
Gentoo 1 118Die Confusion Matrix ist deshalb so wertvoll, weil sie nicht nur die Gesamtleistung zeigt, sondern auch welche Art von Fehlern das Modell macht. In unserem Fall sehen wir, dass Modell 1 gelegentlich beide Arten verwechselt (11 FP, 13 FN), während Modell 2 fast perfekt ist (nur 1 FP, 1 FN).
# Berechnung der Metriken
def calculate_metrics(cm):
tn, fp, fn, tp = cm.ravel()
sensitivity = tp / (tp + fn) # True Positive Rate, Recall
specificity = tn / (tn + fp) # True Negative Rate
precision = tp / (tp + fp) # Positive Predictive Value
accuracy = (tp + tn) / (tp + tn + fp + fn)
return sensitivity, specificity, precision, accuracy
sens1, spec1, prec1, acc1 = calculate_metrics(cm1)
sens2, spec2, prec2, acc2 = calculate_metrics(cm2)
print("KLASSIFIKATIONSMETRIKEN")
print("=" * 50)
print(" Modell 1 Modell 2")
print(f"Sensitivity (Recall) {sens1:.3f} {sens2:.3f}")
print(f"Specificity {spec1:.3f} {spec2:.3f}")
print(f"Precision {prec1:.3f} {prec2:.3f}")
print(f"Accuracy {acc1:.3f} {acc2:.3f}")KLASSIFIKATIONSMETRIKEN
==================================================
Modell 1 Modell 2
Sensitivity (Recall) 0.891 0.992
Specificity 0.925 0.993
Precision 0.906 0.992
Accuracy 0.909 0.992Sensitivity und Specificity: Fokus auf einzelne Klassen
Sensitivity (auch Recall oder True Positive Rate genannt) misst den Anteil der korrekt identifizierten positiven Fälle. In unserem Kontext: “Von allen Gentoo-Pinguinen, wie viele hat das Modell richtig erkannt?” Modell 1 erreicht 89.1%, Modell 2 beeindruckende 99.2%. Sensitivity ist besonders wichtig in Anwendungen, wo das Übersehen positiver Fälle schwerwiegende Folgen hat (z.B. Krankheitsdiagnose).
Specificity (True Negative Rate) ist das Pendant für negative Fälle: “Von allen Adelie-Pinguinen, wie viele wurden korrekt als solche erkannt?” Beide Modelle zeigen hier exzellente Werte (92.5% bzw. 99.3%). Specificity ist entscheidend, wenn False Positives problematisch sind (z.B. bei Spam-Filtern, wo wichtige E-Mails nicht fälschlicherweise blockiert werden sollen).
Das Verhältnis zwischen Sensitivity und Specificity ist oft ein Trade-off: Erhöht man den Schwellenwert, steigt die Specificity (weniger False Positives), aber die Sensitivity sinkt (mehr False Negatives). Dieses Spannungsfeld ist zentral für die Optimierung von Klassifikationsmodellen.
Precision: Die Verlässlichkeit positiver Vorhersagen
Precision (auch Positive Predictive Value) beantwortet eine andere Frage: “Von allen als Gentoo klassifizierten Pinguinen, wie viele sind tatsächlich Gentoo?” Mit 90.6% (Modell 1) bzw. 99.2% (Modell 2) zeigen beide Modelle hohe Präzision.
Der Unterschied zwischen Precision und Sensitivity wird oft missverstanden: Sensitivity fragt “Wie viele der echten Gentoos habe ich gefunden?”, während Precision fragt “Wie viele meiner Gentoo-Vorhersagen sind richtig?”. In unausgewogenen Datensätzen kann diese Unterscheidung kritisch werden.
Accuracy: Der intuitive, aber oft irreführende Gesamtwert
Accuracy ist die wohl intuitivste Metrik: “Wie viele Vorhersagen insgesamt waren richtig?” Beide Modelle zeigen hervorragende Accuracy-Werte (90.9% bzw. 99.2%). Allerdings ist Accuracy bei unausgewogenen Datensätzen problematisch. Wenn 95% der Fälle zur Mehrheitsklasse gehören, erzielt ein “dummer” Klassifikator, der immer die Mehrheitsklasse vorhersagt, bereits 95% Accuracy. In unserem Fall ist der Datensatz relativ ausgewogen (146 Adelie, 119 Gentoo), weshalb Accuracy hier aussagekräftig ist.
ROC-Kurve und AUC: Schwellenwert-unabhängige Bewertung
Nun haben wir schon so einiges ausgerechnet und verglichen, aber was wir weiterhin nicht verändert haben ist der Schwellenwert von 0.5, der die Wahrscheinlichkeiten in binäre Klassifikationen umwandelt. Auch dieser ist ja letztendlich eine Stellschraube, die die Performance des jeweiligen Modells beeinflusst. Anstatt nun noch ein paar weitere Schwellenwerte auszuprobieren, probieren wir direkt alle und fassen das Ergebnis visuell zusammen:
# ROC-Kurven
fpr1, tpr1, _ = roc_curve(y_true, prob1);
fpr2, tpr2, _ = roc_curve(y_true, prob2);
auc1 = auc(fpr1, tpr1);
auc2 = auc(fpr2, tpr2);
fig, ax = plt.subplots(figsize=(8, 6), layout='tight')
ax.plot(fpr1, tpr1, linewidth=2, alpha=0.5, label=f'Modell 1 (AUC = {auc1:.3f})');
ax.plot(fpr2, tpr2, linewidth=2, alpha=0.5, label=f'Modell 2 (AUC = {auc2:.3f})');
ax.plot([0, 1], [0, 1], 'k--', alpha=0.5, label='Zufall (AUC = 0.5)');
ax.set_xlabel('False Positive Rate (1 - Specificity)');
ax.set_ylabel('True Positive Rate (Sensitivity)');
ax.set_title('ROC-Kurven: Modellvergleich');
ax.legend();
ax.grid(True, alpha=0.3)
plt.show()
print(f"AUC-Werte:")
print(f"Modell 1: {auc1:.3f}")
print(f"Modell 2: {auc2:.3f}")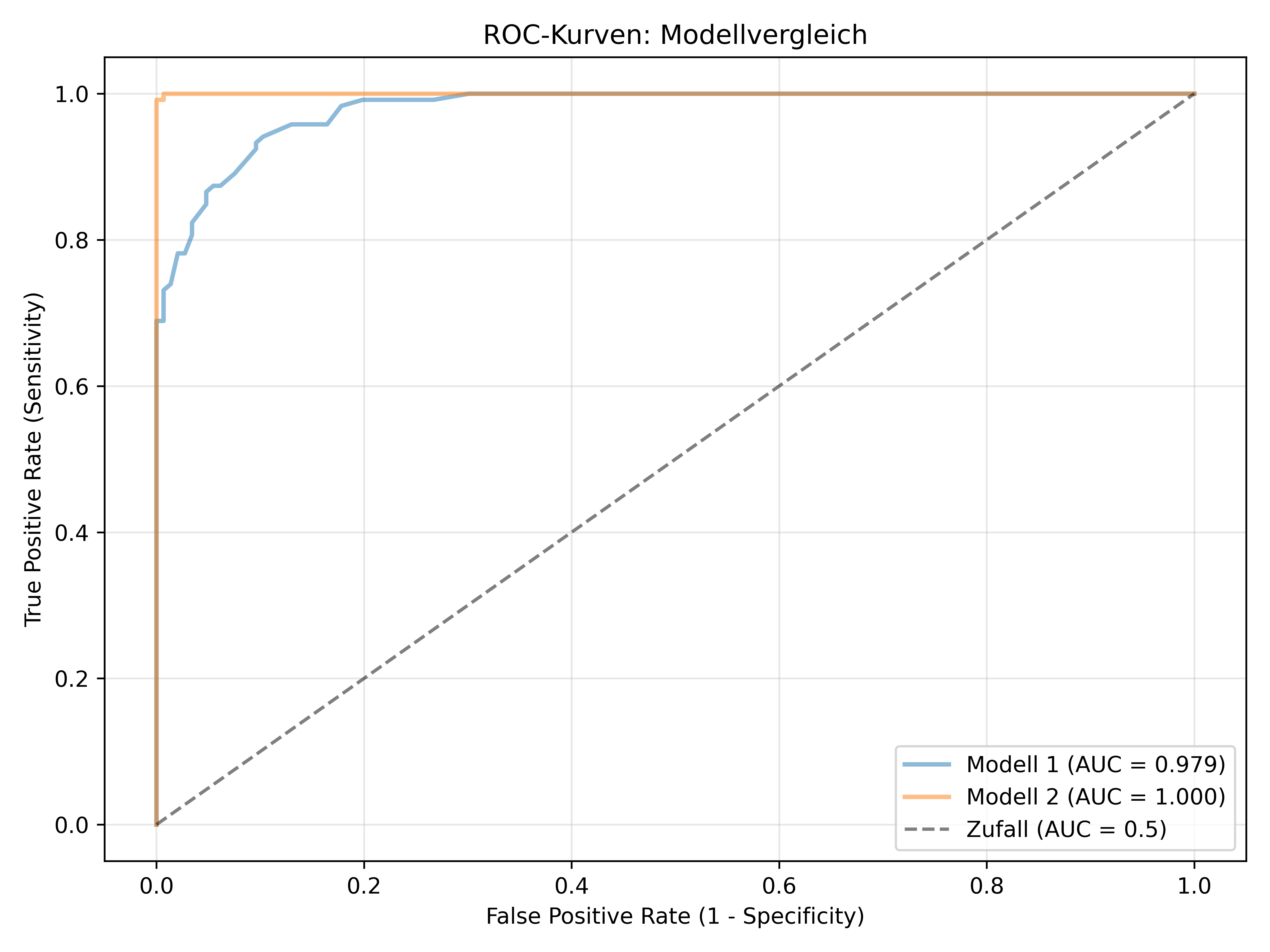
AUC-Werte:
Modell 1: 0.979
Modell 2: 1.000Die ROC-Kurve (Receiver Operating Characteristic) ist ein mächtiges Werkzeug, das die Leistung über alle möglichen Schwellenwerte hinweg visualisiert. Sie zeigt das Verhältnis von True Positive Rate (Sensitivity) zu False Positive Rate (1 - Specificity). Eine perfekte ROC-Kurve würde durch die Punkte (0,0), (0,1), (1,1) verlaufen - ein rechter Winkel in der oberen linken Ecke.
AUC (Area Under the Curve) fasst die ROC-Kurve in einer einzigen Zahl zusammen, indem die Fläche unter der Kurve berechnet wird. Ein AUC von 1.0 bedeutet perfekte Klassifikation, 0.5 entspricht purem Zufall. Modell 1 erreicht bereits exzellente 0.979, Modell 2 ist mit 1.0 praktisch perfekt.
Der große Vorteil der AUC liegt darin, dass sie als einzelner Kennwert die gesamte ROC-Kurve zusammenfasst und damit die Schwellenwert-Unabhängigkeit der Modellleistung kompakt quantifiziert. Das macht sie besonders nützlich für den Vergleich und die Auswahl von Modellen.
Precision-Recall-Kurve: Alternative für unausgewogene Datensätze
Neben der ROC-Kurve gibt es eine weitere nennenswerte Bewertungsmethode: die Precision-Recall-Kurve. Diese zeigt das Verhältnis von Precision zu Recall (Sensitivity) über alle möglichen Schwellenwerte. Während ROC-Kurven bei stark unausgewogenen Datensätzen irreführend optimistisch sein können, bleiben Precision-Recall-Kurven auch in solchen Fällen aussagekräftig.
from sklearn.metrics import precision_recall_curve, average_precision_score
# Precision-Recall-Kurven
prec1, rec1, _ = precision_recall_curve(y_true, prob1)
prec2, rec2, _ = precision_recall_curve(y_true, prob2)
# Average Precision Score (Fläche unter PR-Kurve)
ap1 = average_precision_score(y_true, prob1)
ap2 = average_precision_score(y_true, prob2)
fig, ax = plt.subplots(figsize=(8, 6), layout='tight')
ax.plot(rec1, prec1, linewidth=2, alpha=0.5, label=f'Modell 1 (AP = {ap1:.3f})');
ax.plot(rec2, prec2, linewidth=2, alpha=0.5, label=f'Modell 2 (AP = {ap2:.3f})');
# Baseline für zufällige Klassifikation
baseline = len(y_true[y_true==1]) / len(y_true)
ax.axhline(y=baseline, color='gray', linestyle='--', alpha=0.7,
label=f'Baseline (AP = {baseline:.3f})');
ax.set_xlabel('Recall (Sensitivity)');
ax.set_ylabel('Precision');
ax.set_title('Precision-Recall-Kurven: Modellvergleich');
ax.legend();
ax.grid(True, alpha=0.3)
plt.show()
print(f"Average Precision Scores:")
print(f"Modell 1: {ap1:.3f}")
print(f"Modell 2: {ap2:.3f}")
print(f"Baseline (Zufall): {baseline:.3f}")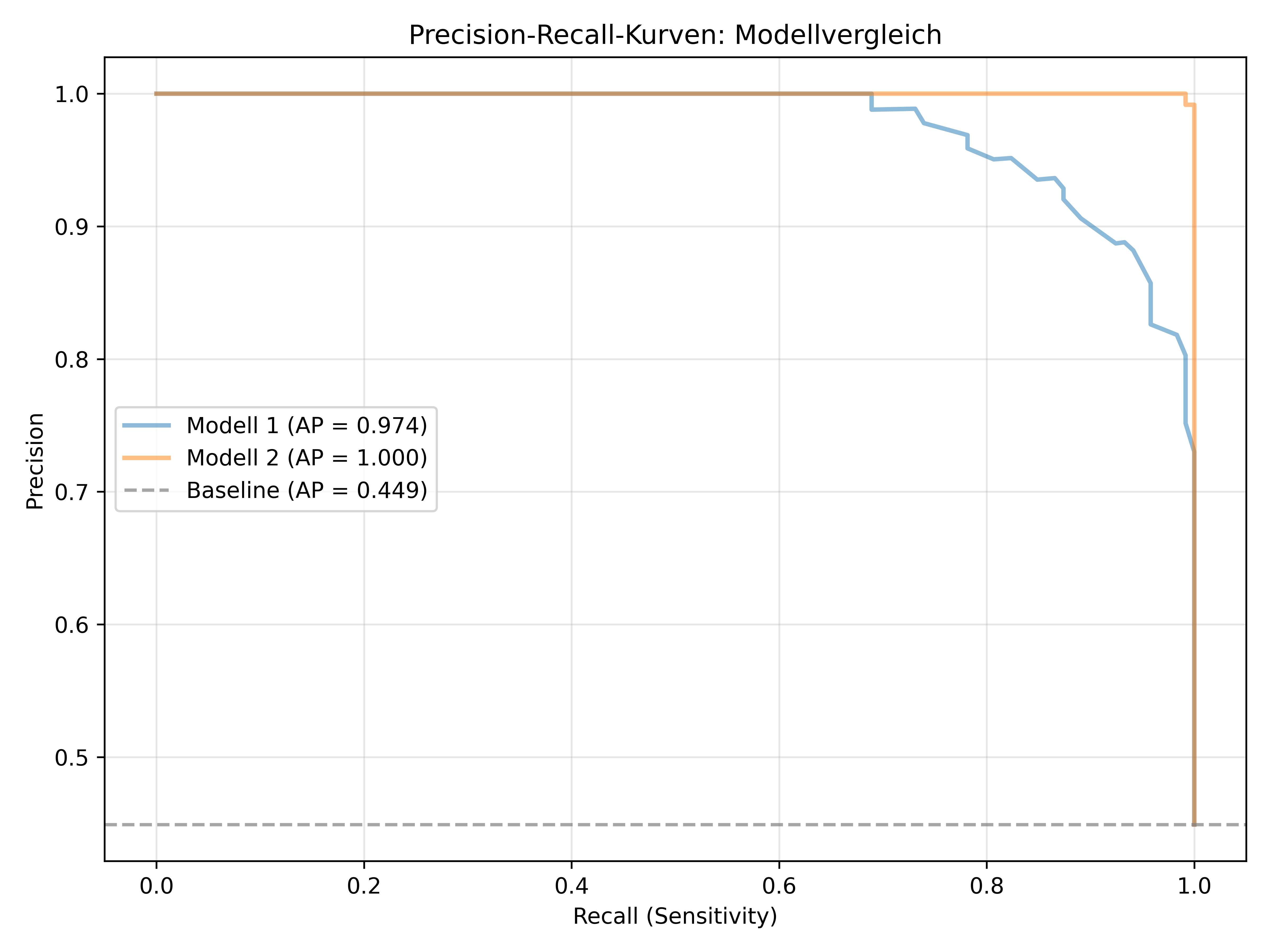
Average Precision Scores:
Modell 1: 0.974
Modell 2: 1.000
Baseline (Zufall): 0.449Wann ROC vs. Precision-Recall verwenden?
ROC-Kurven sind ideal bei ausgewogenen Datensätzen und wenn sowohl True Positives als auch True Negatives gleich wichtig sind. Sie zeigen die Gesamttrennfähigkeit sehr gut.
Precision-Recall-Kurven sind besser bei unausgewogenen Datensätzen geeignet, besonders wenn die positive Klasse selten ist. Sie fokussieren auf die Leistung bei der Minderheitsklasse und sind weniger von der großen Anzahl True Negatives beeinflusst.
Beispiel: Bei einem Datensatz mit 95% negativen und 5% positiven Fällen kann ein Klassifikator mit 95% Accuracy alle Fälle als negativ klassifizieren. Die ROC-Kurve würde gut aussehen (hohe Specificity), aber die Precision-Recall-Kurve würde die schlechte Leistung bei der wichtigen Minderheitsklasse enthüllen.
In unserem relativ ausgewogenen Pinguin-Datensatz (55% Adelie, 45% Gentoo) zeigen beide Kurventypen ähnliche Ergebnisse. Dennoch ist es wichtig, beide Perspektiven zu kennen, da sie unterschiedliche Aspekte der Modellleistung beleuchten.
Die Landschaft der Metriken: Wann welche verwenden?
Die verschiedenen Metriken ergänzen sich und haben unterschiedliche Stärken:
- Confusion Matrix: Liefert das vollständige Bild aller Fehlertypen
- Sensitivity: Wichtig bei hohen Kosten für False Negatives (z.B. Krebsdiagnose)
- Specificity: Entscheidend bei hohen Kosten für False Positives (z.B. Terrorismus-Screening)
- Precision: Relevant bei ressourcenbegrenzten Nachfolgeaktionen (z.B. Marketingkampagnen)
- Accuracy: Sinnvoll bei ausgewogenen Datensätzen und gleichen Kosten für alle Fehlertypen
- AUC (ROC): Ideal für Modellvergleiche bei ausgewogenen Datensätzen
- Average Precision (PR): Besser für unausgewogene Datensätze und Fokus auf Minderheitsklasse
In unserem Fall zeigen alle Metriken eindeutig die Überlegenheit von Modell 2. Die nahezu perfekten Werte (alle >99%) bestätigen jedoch auch unsere Warnung bezüglich quasi-complete separation: Das Modell ist möglicherweise zu spezifisch für unseren Datensatz optimiert.
sklearn: Vorgefertigte Funktionen für effiziente Analyse
Die meisten der Berechnungen, die wir manuell durchgeführt haben, können mit sklearn-Funktionen deutlich effizienter erledigt werden. Die scikit-learn-Bibliothek ist ja wie gesagt mehr auf Machine Learning ausgereichtet und bietet vorgefertigte Funktionen für praktisch alle Klassifikationsmetriken:
from sklearn.metrics import (classification_report, roc_auc_score,
average_precision_score, confusion_matrix,
RocCurveDisplay, PrecisionRecallDisplay,
ConfusionMatrixDisplay)
print(classification_report(y_true, pred1,
target_names=['Adelie', 'Gentoo'],
digits=3))
print(f"ROC AUC: {roc_auc_score(y_true, prob1):.3f}")
print(f"Precision-Recall AUC: {average_precision_score(y_true, prob1):.3f}") precision recall f1-score support
Adelie 0.912 0.925 0.918 146
Gentoo 0.906 0.891 0.898 119
accuracy 0.909 265
macro avg 0.909 0.908 0.908 265
weighted avg 0.909 0.909 0.909 265
ROC AUC: 0.979
Precision-Recall AUC: 0.974# Confusion Matrix Plot
fig, ax = plt.subplots(figsize=(6, 5), layout='tight')
ConfusionMatrixDisplay.from_predictions(
y_true, pred1,
display_labels=['Adelie', 'Gentoo'],
ax=ax
);
plt.show()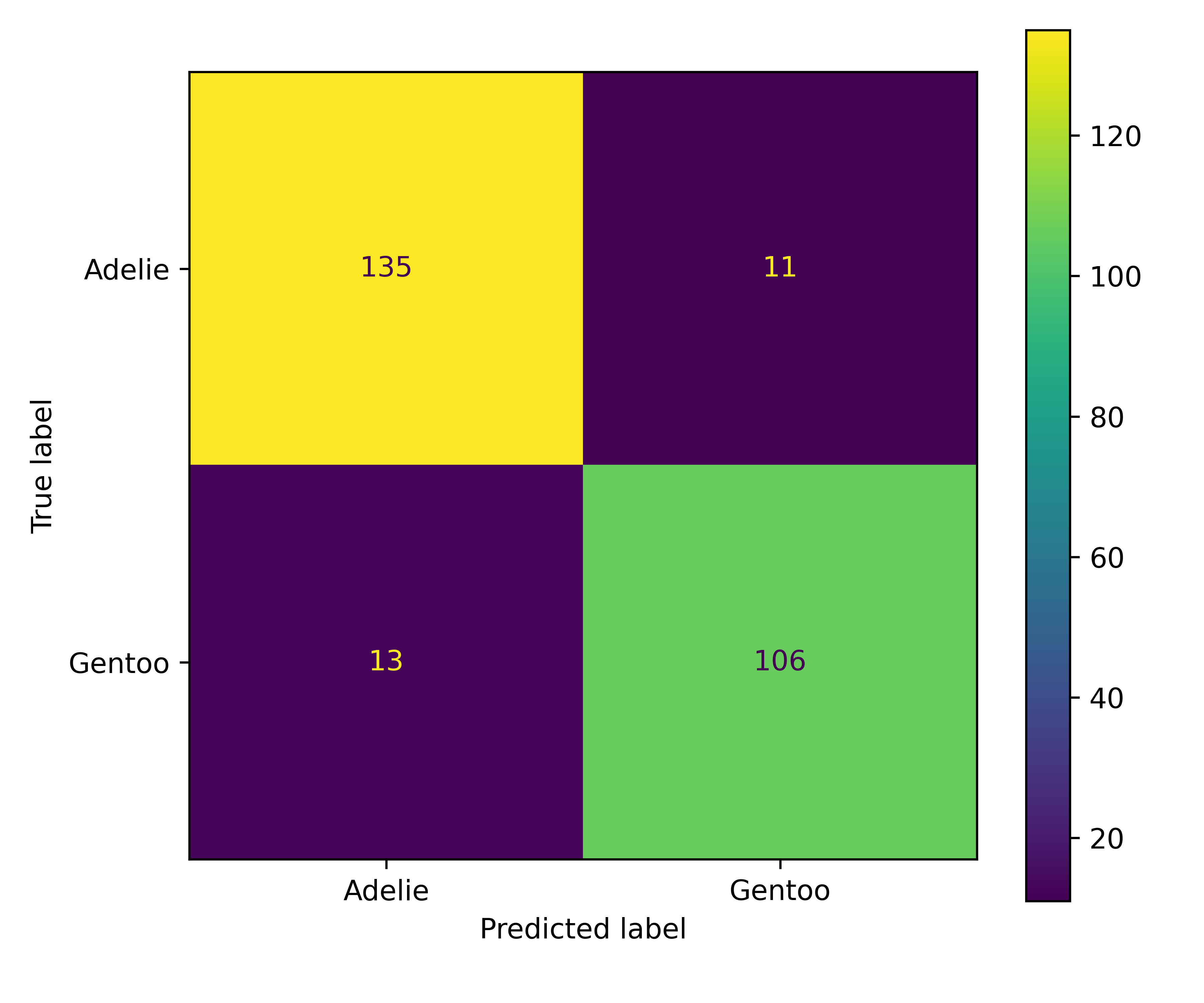
# ROC Curve Plot
fig, ax = plt.subplots(figsize=(6, 5), layout='tight')
RocCurveDisplay.from_predictions(
y_true, prob1,
ax=ax
);
plt.show()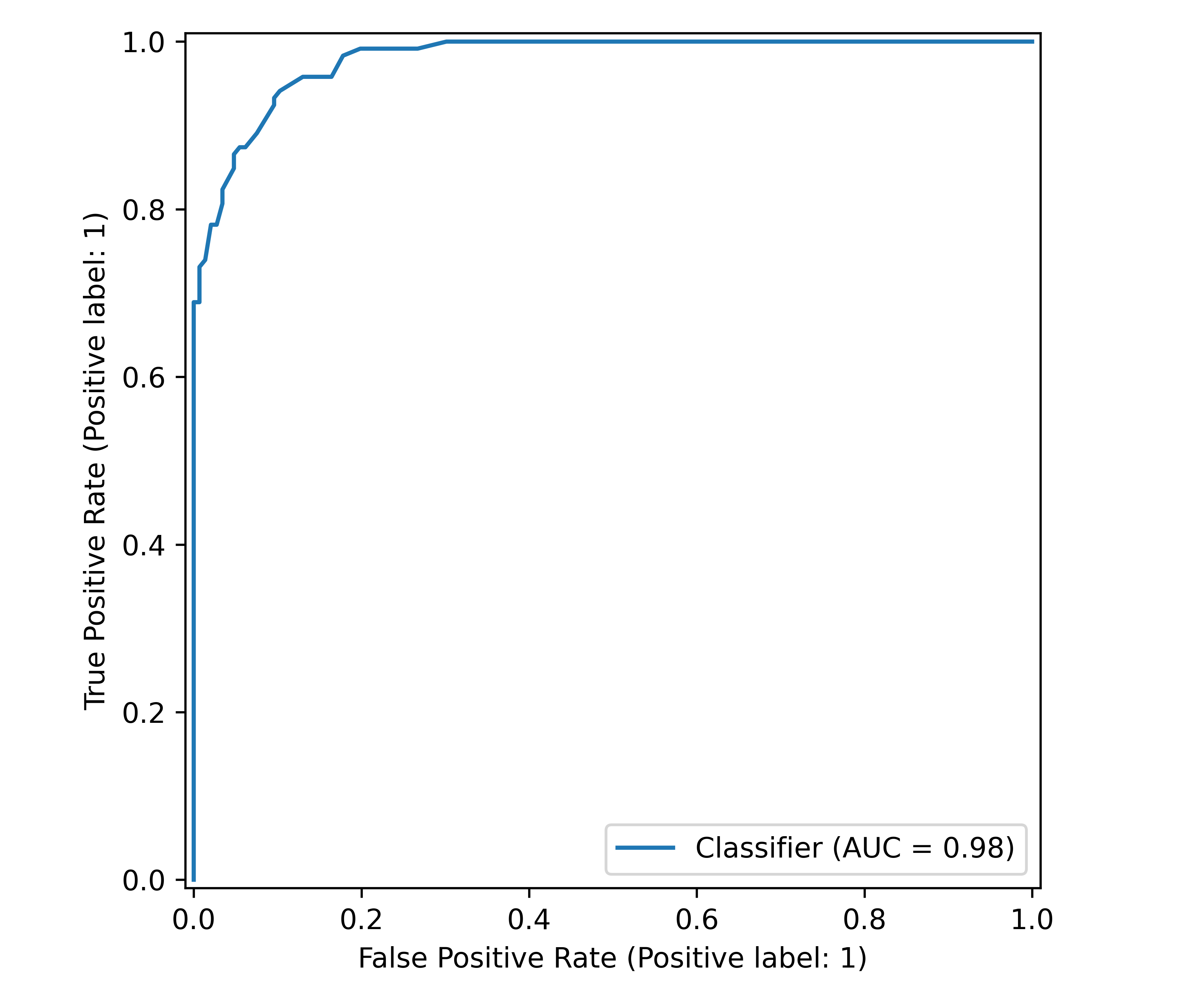
# Precision-Recall Curve Plot
fig, ax = plt.subplots(figsize=(6, 5), layout='tight')
PrecisionRecallDisplay.from_predictions(
y_true, prob1,
ax=ax
);
plt.show()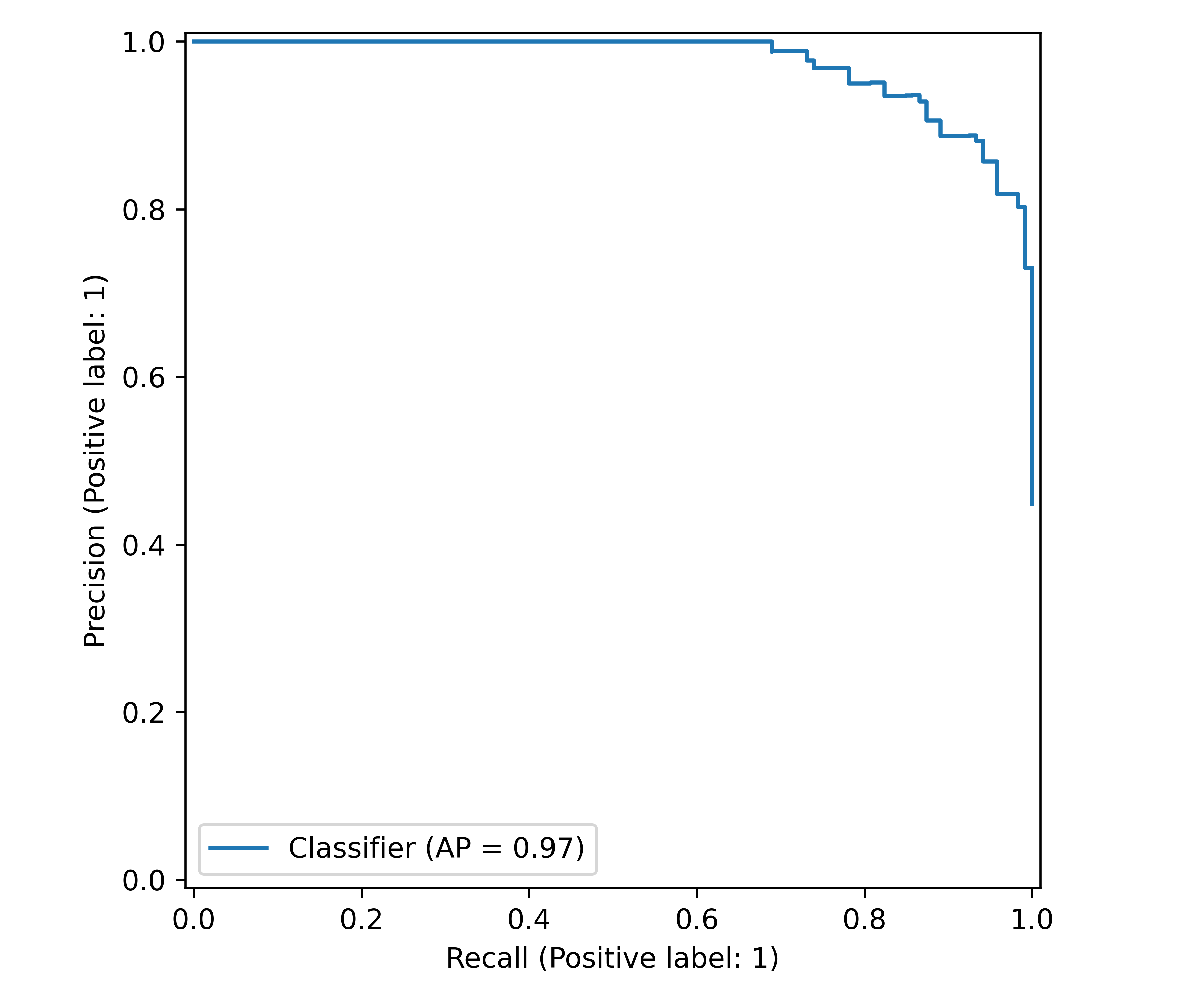
Mit nur wenigen Zeilen Code erhalten wir eine vollständige Bewertung beider Modelle:
-
classification_report()liefert Precision, Recall, F1-Score und Support für jede Klasse -
confusion_matrix()erstellt die Konfusionsmatrix -
roc_auc_score()undaverage_precision_score()berechnen die AUC-Werte
Der F1-Score, den wir vorher nicht erwähnt hatten, ist das harmonische Mittel von Precision und Recall: F1 = 2 × (Precision × Recall) / (Precision + Recall). Er ist besonders nützlich, wenn man ein einzelnes Maß für die Balance zwischen Precision und Recall benötigt.
Die sklearn-Funktionen sparen nicht nur Zeit, sondern reduzieren auch Fehlerquellen bei der manuellen Berechnung und bieten konsistente Implementierungen, die in der gesamten Data Science-Community verwendet werden.
- Machine Learning Fundamentals: The Confusion Matrix
- Machine Learning Fundamentals: Sensitivity and Specificity
- ROC and AUC, Clearly Explained!
- ROC-Kurve und AUC-Wert (Einfach erklärt)
- ROC & AUC - A Visual Explanation of Receiver Operating Characteristic Curves and Area Under the Curve
- Precision & Recall - Accuracy Is Not Enough
Übungen
Übung 1: Titanic-Überlebensanalyse
In dieser Übung wendest du die Konzepte der multiplen logistischen Regression auf den Titanic-Datensatz an. Führe einen systematischen Modellvergleich mit allen Kombinationen der Variablen age, sex und pclass durch.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.formula.api as smf
from sklearn.metrics import confusion_matrix, roc_curve, auc
np.random.seed(42)
# Titanic-Datensatz über seaborn laden
titanic = sns.load_dataset("titanic")
# Fehlende Werte entfernen für age, sex und pclass
titanic_clean = titanic[['survived', 'age', 'sex', 'pclass']].dropna()
print(f"Anzahl Beobachtungen: {len(titanic_clean)}")
print(f"Überlebensrate: {titanic_clean['survived'].mean():.3f}")Anzahl Beobachtungen: 714
Überlebensrate: 0.406Aufgabe: Passe die folgenden 7 Modelle an und erstelle eine Vergleichstabelle sowie ROC-Kurven:
survived ~ age-
survived ~ C(sex)
survived ~ C(pclass)survived ~ age + C(sex)survived ~ age + C(pclass)survived ~ C(sex) + C(pclass)survived ~ age + C(sex) + C(pclass)
Die Ergebnistabelle soll folgende Spalten enthalten: Modell, AIC, Pseudo_R2, Log_Likelihood, Accuracy, Sensitivity, Specificity, Precision.
Zusätzlich erstelle ROC-Kurven für alle Modelle in einem Plot mit AUC-Werten in der Legende.
Fußnoten
Zur Erinnerung: Letzter testet, ob das der zusätzliche Faktor Geschlecht das Modell signifikant verbessert. Ein p-Wert < 0.05 zeigt, dass Modell 2 statistisch signifikant besser ist als Modell 1.↩︎