import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.stats as stats
import statsmodels.api as sm
import statsmodels.formula.api as smf
from sklearn.model_selection import (train_test_split, cross_val_score, cross_validate,
KFold, StratifiedKFold, LeaveOneOut,
RepeatedKFold, RepeatedStratifiedKFold)
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
np.random.seed(42)Train-Test-Split & Kreuzvalidierung
In den vorangegangenen Kapiteln haben wir verschiedene statistische Modelle kennengelernt. Dabei haben wir uns bisher hauptsächlich darauf konzentriert, wie gut unsere Modelle zu den vorhandenen Daten passen. Doch eine entscheidende Frage haben wir noch nicht beantwortet: Wie gut funktionieren unsere Modelle bei neuen, bisher ungesehenen Daten?
Man kann argumentieren, dass diese Frage besonders wichtig ist, da wir unsere Modelle ggf. nicht nur bauen, um die vorhandenen Daten zu beschreiben, sondern um Vorhersagen für neue Situationen zu treffen. Hier kommen Konzepte ins Spiel, die zum Herzstück des Machine Learning gehören: Train-Test-Split und Kreuzvalidierung.
Wir waren thematisch übrigens schon mal relativ dicht an der Motivation für dieses Vorgehen hier: Als wir in Kapitel 3.7 über das Polynom 10. Grades und Overfitting gesprochen haben. Dort wurde klar, dass man ein einzelnes Modell natürlich immer weiter anspassen kann, um die Daten perfekt zu beschreiben. Aber das führt eben nicht zu besseren Vorhersagen für neue Daten. Genau das ist der Kern von Train-Test-Split und Kreuzvalidierung: Wir wollen Modelle bauen, die nicht nur gut auf den Trainingsdaten funktionieren, sondern auch auf neuen, ungesehenen Daten.
Das Problem mit “In-Sample” Evaluation
Bisher haben wir unsere Modelle hauptsächlich mit In-Sample Metriken bewertet - R², F-Statistiken und p-Werte, die alle auf denselben Daten basieren, die wir zum Anpassen des Modells verwendet haben. Das ist ein wenig so, als würde man Schüler mit genau denselben Aufgaben testen, mit denen sie geübt haben.
Schauen wir uns das Problem anhand eines einfachen Beispiels an.
Ein einfaches visuelles Beispiel
Wir verwenden die ersten 100 Gentoo-Pinguine aus unserem bekannten Palmer Penguins Datensatz und schauen uns die Beziehung zwischen Flügellänge und Körpergewicht an:
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
# Erste 100 Gentoo-Pinguine ohne fehlende Werte
gentoo_small = (penguins
.query("species == 'Gentoo'")
[['flipper_length_mm', 'body_mass_g']]
.dropna()
.head(100))
Zunächst passen wir eine lineare Regression an alle 100 Datenpunkte an:
# Lineare Regression mit allen Daten
X_all = gentoo_small[['flipper_length_mm']]
y_all = gentoo_small['body_mass_g']
model_all = LinearRegression()
model_all.fit(X_all, y_all);
# Vorhersagen für Plotting
X_plot = np.linspace(X_all.min(), X_all.max(), 100).reshape(-1, 1)
y_pred_all = model_all.predict(X_plot)
# R² berechnen
r2_all = r2_score(y_all, model_all.predict(X_all))
print(f"R² (alle Daten): {r2_all:.3f}")R² (alle Daten): 0.512Code zeigen/verstecken
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
ax.scatter(X_all, y_all, color='purple', s=80, alpha=0.8, label='Alle Datenpunkte')
ax.plot(X_plot, y_pred_all, color='purple', linewidth=2, label=f'Regression alle Daten (R² = {r2_all:.3f})')
ax.set_xlabel('Flügellänge (mm)')
ax.set_ylabel('Körpergewicht (g)')
ax.set_title('Lineare Regression: Alle 100 Gentoo-Pinguine')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()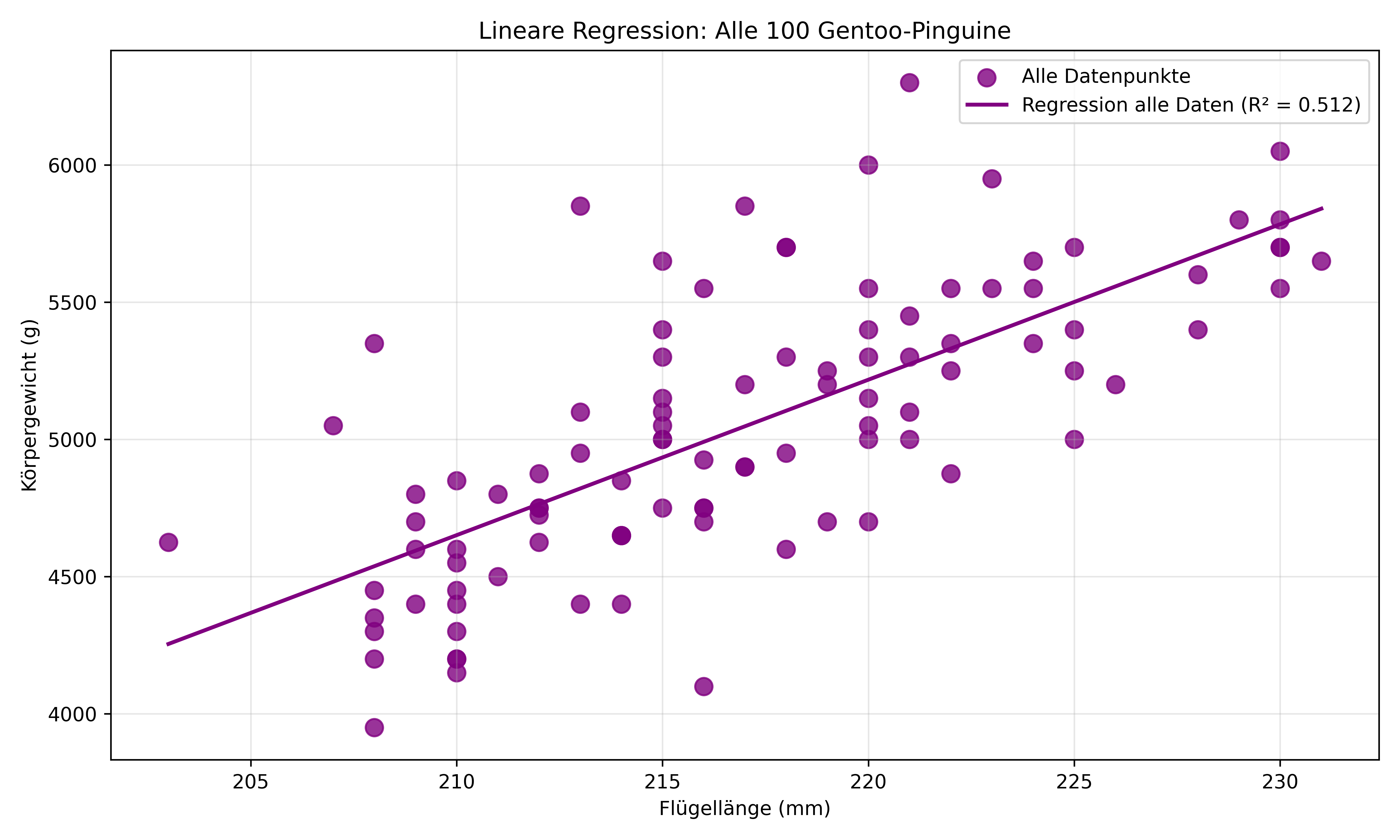
So weit so gut - so kennen wir es schon.
Jetzt teilen wir die Daten in Trainings- und Testdaten auf. Zunächst nehmen wir die ersten 80 Punkte zum Trainieren und die letzten 20 Punkte zum Testen. Das Modell anpassen mit Trainingsdaten ist also prinzipiell identisch zu dem was wir eben getan haben, nur eben mit einem Teildatensatz (80 Pinguine) statt den ganzen 100 Pinguinen. Der zweite Schritt ist aber neu: Wir nehmen dann das Modell basierend auf den Trainingsdaten und verwenden es, um Vorhersagen für die Testdaten (die letzten 20 Pinguine) zu machen. Das ist der entscheidende Schritt, um zu sehen, wie gut unser Modell bei neuen Daten funktioniert.
# Train-Test-Split: 80 für Training, 20 für Test
# (Wir nehmen erstmal die ersten 80 vs. letzten 20 - später lernen wir zufällige Aufteilung)
X_train = gentoo_small[['flipper_length_mm']].iloc[:80] # 0-79
y_train = gentoo_small['body_mass_g'].iloc[:80] # 0-79
X_test = gentoo_small[['flipper_length_mm']].iloc[80:] # 80-99
y_test = gentoo_small['body_mass_g'].iloc[80:] # 80-99
# Modell nur auf Trainingsdaten anpassen
model_train = LinearRegression()
model_train.fit(X_train, y_train);
# Vorhersagen für das Plotting
y_pred_train = model_train.predict(X_plot)
print(f"Trainingsdaten: {len(X_train)} Punkte")
print(f"Testdaten: {len(X_test)} Punkte")Trainingsdaten: 80 Punkte
Testdaten: 20 PunkteCode zeigen/verstecken
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
# Trainingspunkte (blau)
ax.scatter(X_train, y_train, color='blue', s=50, alpha=0.6, label='Trainingsdaten (80 Punkte)')
# Testpunkte (rot)
ax.scatter(X_test, y_test, color='red', s=60, alpha=0.8, label='Testdaten (20 Punkte)')
# Beide Regressionsgeraden
ax.plot(X_plot, y_pred_all, color='purple', linewidth=2, linestyle='--',
label=f'Regression alle Daten')
ax.plot(X_plot, y_pred_train, color='blue', linewidth=2,
label=f'Regression nur Training')
ax.set_xlabel('Flügellänge (mm)')
ax.set_ylabel('Körpergewicht (g)')
ax.set_title('Train-Test-Split: Modell basiert nur auf blauen Punkten')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()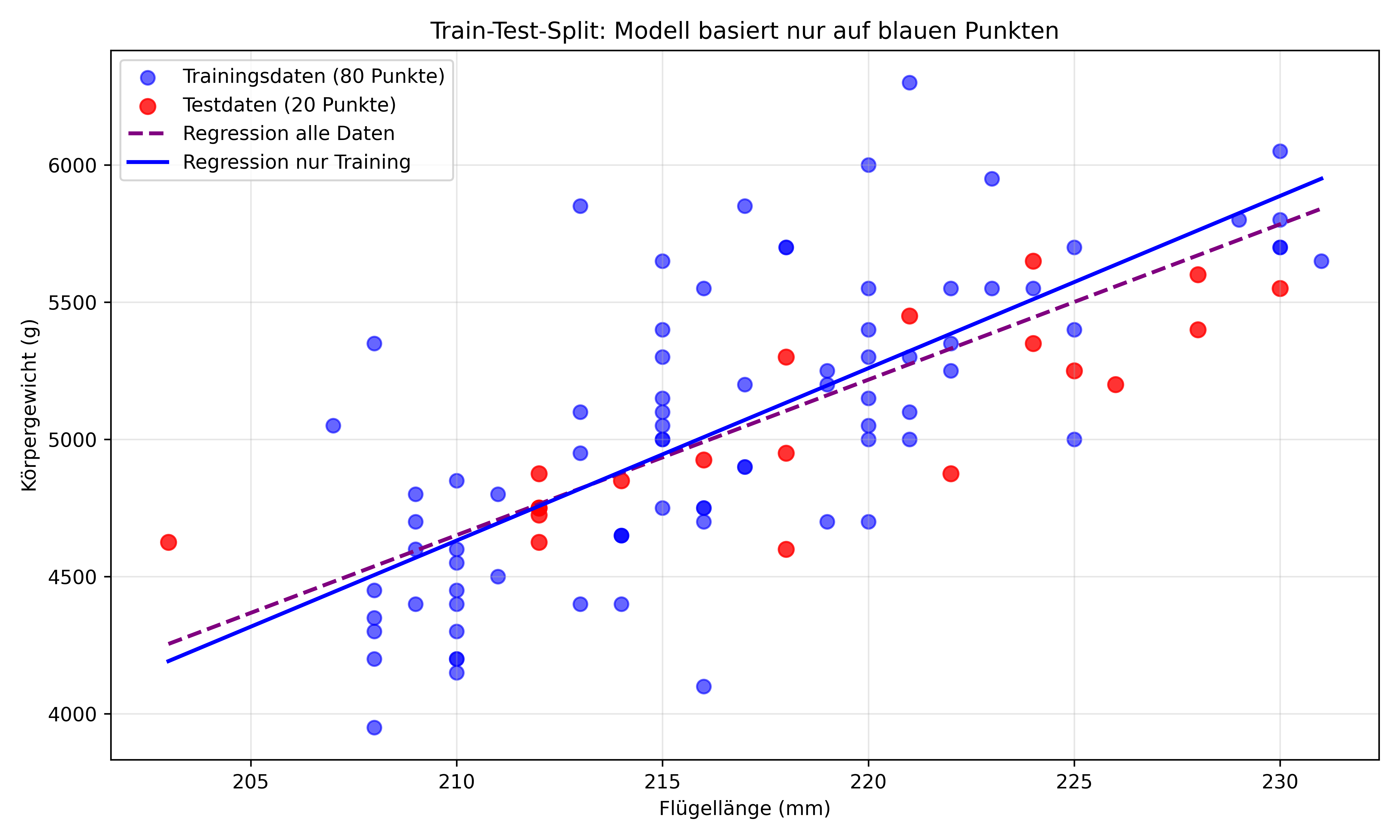
Hier können wir bereits sehen, dass die beiden Regressionsgeraden leicht unterschiedlich sind. Die blaue Gerade basiert nur auf den 80 Trainingspunkten, während die lila gestrichelte Gerade auf allen 100 Punkten basiert (diese hatten wir oben schon gesehen).
Aber jetzt kommt der entscheidende Schritt: Wir nehmen das Modell basierend auf den Trainingsdaten (blaue Linie basierend auf den 80 blauen Punkten) und verwenden es, um Vorhersagen für die Testdaten (die roten 20 Punkte) zu machen.
R2 für “Out-of-Sample” Evaluation
Bisher haben wir R² immer so berechnet: Ein Datensatz, ein Modell das zu diesem Datensatz passt, und dann das R² für genau diesen Datensatz. Das ist “In-Sample” Evaluation.
Aber es gibt noch eine andere Art R² zu verwenden: “Out-of-Sample” Evaluation. Dabei verwenden wir ein Modell, das auf einem Datensatz trainiert wurde, um Vorhersagen für einen anderen Datensatz zu machen. Wir können direkt mittels r2_score das R² für die Trainings- und Testdaten berechnen, um zu sehen, wie gut das Modell auf den Trainingsdaten funktioniert und wie gut es die Testdaten vorhersagt.
# In-Sample R² (wie gewohnt): Trainingsdaten + Modell basiert auf Trainingsdaten
y_train_pred = model_train.predict(X_train)
r2_train = r2_score(y_train, y_train_pred)
# Out-of-Sample R² (neu!): Testdaten + Modell basiert auf Trainingsdaten
y_test_pred = model_train.predict(X_test)
r2_test = r2_score(y_test, y_test_pred)
print(f"R² (Trainingsdaten - In-Sample): {r2_train:.3f}")
print(f"R² (Testdaten - Out-of-Sample): {r2_test:.3f}")
print(f"Unterschied: {r2_train - r2_test:.3f}")R² (Trainingsdaten - In-Sample): 0.515
R² (Testdaten - Out-of-Sample): 0.386
Unterschied: 0.129Code zeigen/verstecken
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
# Trainingspunkte (blau)
ax.scatter(X_train, y_train, color='blue', s=50, alpha=0.6, label='Trainingsdaten (80 Punkte)')
# Testpunkte (rot)
ax.scatter(X_test, y_test, color='red', s=60, alpha=0.8, label='Testdaten (20 Punkte)')
# Regressionsgerade (basiert nur auf Training)
ax.plot(X_plot, y_pred_train, color='blue', linewidth=2,
label=f'Regression Trainingsdaten')
ax.set_xlabel('Flügellänge (mm)')
ax.set_ylabel('Körpergewicht (g)')
ax.set_title('Train-Test-Split: Wie gut passt das Trainings-Modell zu den Test-Daten?')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()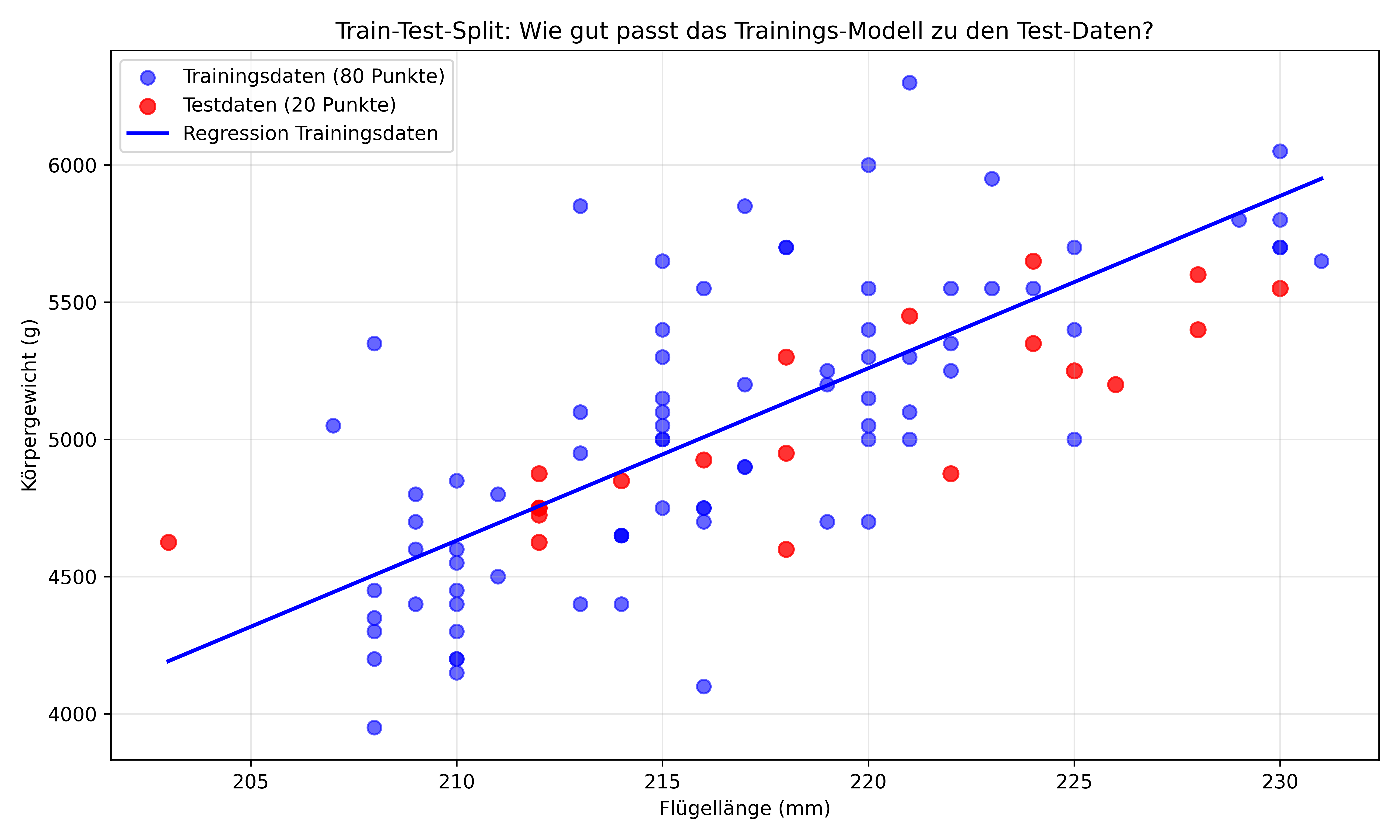
Das zeigt das fundamentale Problem: Ein Modell wird fast immer besser auf den Trainingsdaten abschneiden als auf neuen, ungesehenen Daten. Das Out-of-Sample R² (Testdaten) ist niedriger als das In-Sample R² (Trainingsdaten). Diese Out-of-Sample Metriken geben uns einen viel realistischeren Eindruck davon, wie gut unser Modell bei neuen Daten funktionieren wird.
Das ganze gilt natürlich nicht nur für R², sondern auch für andere Metriken/Loss-Funktionen wie den Mean Absolute Error (MAE) oder den Root Mean Squared Error (RMSE) usw. All diese Metriken können wir ebenfalls für Trainings- und Testdaten berechnen, um die Performance des Modells zu bewerten.
Ein wichtiger Unterschied zwischen In-Sample und Out-of-Sample R²: Während In-Sample R² immer zwischen 0 und 1 liegt (sofern das Modell einen Intercept hat), kann Out-of-Sample R² durchaus negativ sein.
Warum kann Out-of-Sample R² negativ sein?
Die Formel für Out-of-Sample R² lautet: \[R^2_{\text{out}} = 1 - \frac{\sum_{i} (y_i - \hat{y}_i)^2}{\sum_{i} (y_i - \bar{y}_{\text{train}})^2}\]
Dabei ist:
- Zähler: Der Vorhersagefehler des Modells auf den Testdaten
- Nenner: Die Varianz der echten Zielwerte in den Testdaten, relativ zum Mittelwert der Trainingsdaten
Wenn das Modell auf den Testdaten schlechter abschneidet als die simple Vorhersage mit dem Mittelwert der Trainingsdaten, wird der Zähler größer als der Nenner – das R² wird negativ.
Warum ist In-Sample R² ≥ 0?
Beim In-Sample R² wird die Modellgüte auf denselben Daten berechnet, auf denen das Modell trainiert wurde: \[R^2_{\text{in}} = 1 - \frac{\text{RSS}}{\text{TSS}} \geq 0\]
Da ein Modell mit Intercept immer mindestens den Mittelwert der Zielvariablen erklären kann, ist der Fehler (RSS) nie größer als die totale Streuung (TSS). Das garantiert \(R^2_{\text{in}} \geq 0\).
Praktische Bedeutung:
- In-Sample R²: zwischen 0 und 1
- Out-of-Sample R²: kann negativ sein
- Ein R² von -0.2 bedeutet: Das Modell ist 20 % schlechter als einfach nur den Mittelwert der Trainingsdaten vorherzusagen.
Train-Test-Split richtig implementieren
In der Praxis teilen wir Daten nicht wie gerade einfach der Reihe nach auf, sondern zufällig. Das ist ein Standard-Vorgehen im Machine Learning und wird z.B. mit der train_test_split Funktion aus scikit-learn implementiert:
# Richtiger Train-Test-Split mit zufälliger Aufteilung
X = gentoo_small[['flipper_length_mm']]
y = gentoo_small['body_mass_g']
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.20, # 20% für Test (20 von 100 Punkten)
shuffle=True, # Durchmischen der Daten vor dem Split
random_state=42 # Für Reproduzierbarkeit
)
print(f"Trainingsdaten: {len(X_train)} Punkte")
print(f"Testdaten: {len(X_test)} Punkte")Trainingsdaten: 80 Punkte
Testdaten: 20 PunkteNun trainieren wir das Modell und bewerten es mit verschiedenen Metriken:
# Modell auf Trainingsdaten anpassen
model = LinearRegression()
model.fit(X_train, y_train);
# Vorhersagen für Training und Test
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)
# Verschiedene Metriken berechnen
def evaluate_model(y_true, y_pred, dataset_name):
r2 = r2_score(y_true, y_pred)
mae = mean_absolute_error(y_true, y_pred)
rmse = np.sqrt(mean_squared_error(y_true, y_pred))
print(f"\n{dataset_name}:")
print(f" R²: {r2:.3f}")
print(f" MAE: {mae:.1f} g")
print(f" RMSE: {rmse:.1f} g")
return {'R²': r2, 'MAE': mae, 'RMSE': rmse}
train_metrics = evaluate_model(y_train, y_train_pred, "Trainingsdaten (In-Sample)")
test_metrics = evaluate_model(y_test, y_test_pred, "Testdaten (Out-of-Sample)")
Trainingsdaten (In-Sample):
R²: 0.527
MAE: 269.2 g
RMSE: 355.0 g
Testdaten (Out-of-Sample):
R²: 0.431
MAE: 272.9 g
RMSE: 347.6 gDies ist ein Kernprinzip des Machine Learning: Modelle müssen auf ungesehenen Daten evaluiert werden.
Das Problem der Variabilität
Ein einzelner Train-Test-Split hat jedoch ein Problem: Die Ergebnisse hängen stark davon ab, welche Datenpunkte zufällig in das Test-Set fallen. Man könnte verschiedene random_state Werte ausprobieren und würde jedes Mal etwas andere Ergebnisse bekommen. Man kann sich natürlich denken, dass man dann ggf. auch mal “Pech” mit dem Split hat und das Modell auf einem Test-Set evaluiert, das nicht repräsentativ für die Gesamtdaten ist. Das führt zu einer hohen Variabilität in den Ergebnissen.
Die naheliegendste Idee um dieses Problem zu umgehen ist wohl einfach mehrere random_state durchlaufen zu lassen und die Resultate zu mitteln. Das ist auch prinzipiell gut, würde aber ein anderes Problem mit sich bringen: Einige unserer Datenpunkte würden dann häufiger in den Trainings- und Test-Sets auftauchen als andere. Abhängig davon was das für Datenpunkte sind, können wir also auch so Verzerrungen bekommen.
Es gibt aber Lösungen für dieses Problem:
K-Fold Cross Validation
Bei der K-Fold Kreuzvalidierung teilen wir die Daten in \(k\) (meist 3-10) gleich große Teile (Folds) auf. Dann verwenden wir abwechselnd \(k-1\) Teile zum Trainieren und \(1\) Teil zum Testen - und das \(k\)-mal. So wird jeder Datenpunkt genau einmal als Test verwendet.
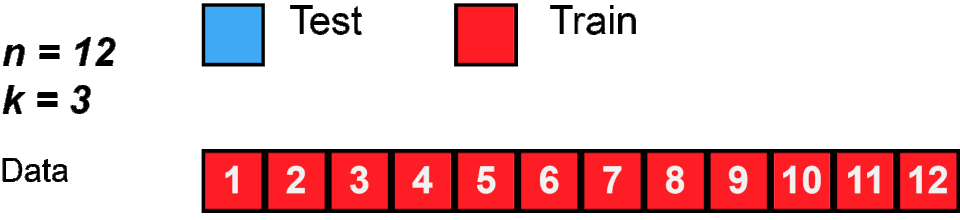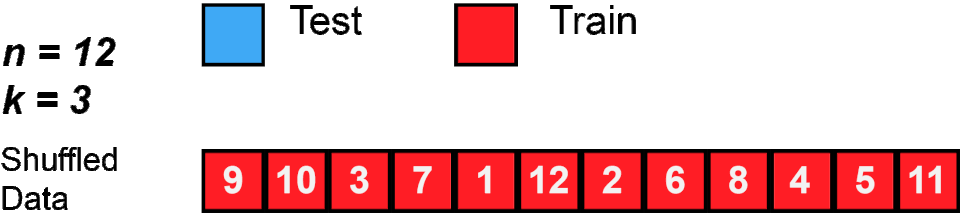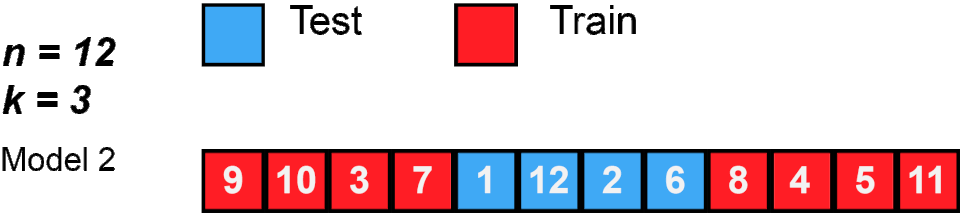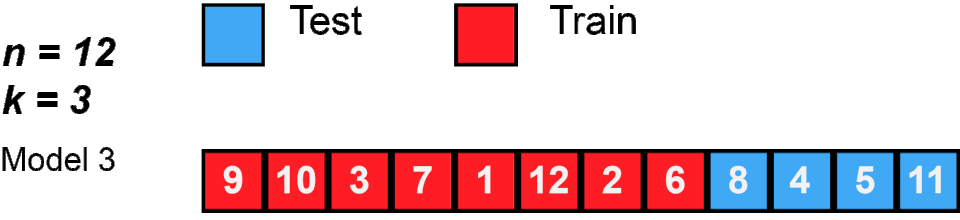
Schauen wir uns zunächst an, wie K-Fold die Indizes aufteilt:
from sklearn.model_selection import KFold
# K-Fold mit 3 Splits
kf = KFold(n_splits=3, shuffle=True, random_state=42)
print("K-Fold Aufteilung der Indizes:")
for fold, (train_index, test_index) in enumerate(kf.split(X), 1):
print(f"Fold {fold}:")
print(f" Train: {train_index}")
print(f" Test: {test_index}")
print("-----")K-Fold Aufteilung der Indizes:
Fold 1:
Train: [ 1 2 3 5 6 7 8 13 14 16 17 19 20 21 23 24 25 27 29 32 34 35 36 37
38 41 43 46 48 49 50 51 52 54 56 57 58 59 60 61 62 63 64 65 66 67 68 71
74 75 78 79 81 82 84 86 87 89 91 92 93 94 95 97 98 99]
Test: [ 0 4 9 10 11 12 15 18 22 26 28 30 31 33 39 40 42 44 45 47 53 55 69 70
72 73 76 77 80 83 85 88 90 96]
-----
Fold 2:
Train: [ 0 1 2 4 9 10 11 12 14 15 18 20 21 22 23 26 28 29 30 31 32 33 37 39
40 41 42 44 45 47 48 51 52 53 55 57 58 59 60 61 63 68 69 70 71 72 73 74
75 76 77 79 80 82 83 84 85 86 87 88 90 91 92 94 96 97 98]
Test: [ 3 5 6 7 8 13 16 17 19 24 25 27 34 35 36 38 43 46 49 50 54 56 62 64
65 66 67 78 81 89 93 95 99]
-----
Fold 3:
Train: [ 0 3 4 5 6 7 8 9 10 11 12 13 15 16 17 18 19 22 24 25 26 27 28 30
31 33 34 35 36 38 39 40 42 43 44 45 46 47 49 50 53 54 55 56 62 64 65 66
67 69 70 72 73 76 77 78 80 81 83 85 88 89 90 93 95 96 99]
Test: [ 1 2 14 20 21 23 29 32 37 41 48 51 52 57 58 59 60 61 63 68 71 74 75 79
82 84 86 87 91 92 94 97 98]
-----Diese Indizes können wir verwenden, um die entsprechenden Datenzeilen zu holen. So wie X.iloc[0] uns die erste Zeile der Daten gibt, so gibt uns dann X.iloc[test_index] eben all die Zeilen, die gerade laut K-Fold im Test-Set sind.
Wir möchten nun also
- Unsere ursprünglichen Daten mittels
KFoldin \(k\) Teile aufteilen - Für jeden Fold:
- Die Trainings- und Test-Indizes holen
- Die Trainings- und Testdaten extrahieren
- Ein Modell auf den Trainingsdaten anpassen
- Vorhersagen für die Testdaten machen
- Metriken wie R², MAE und RMSE berechnen
Das klingt nach viel Arbeit, aber weil genau das das täglich Brot von Data Scientists ist, haben wir dafür natürlich Funktionen in scikit-learn: z.B. cross_val_score. Diese Funktion übernimmt die Aufteilung der Daten, das Anpassen des Modells und die Berechnung der Metriken für uns. Im einfachen Fall geht das so:
cv_r2 = cross_val_score(
estimator=LinearRegression(),
X=gentoo_small[['flipper_length_mm']],
y=gentoo_small['body_mass_g'],
cv=3,
scoring='r2'
)
print(f"3-Fold CV R² Scores: {cv_r2}")
print(f"Durchschnitt: {cv_r2.mean():.3f}")3-Fold CV R² Scores: [0.32377652 0.57349529 0.49602345]
Durchschnitt: 0.464Wir geben also an,
- welches Modell (
estimator): in unserem Fall lineare Regression und demnach die zugehörige sklearn FunktionLinearRegression() - welche Daten (
Xundy): in unserem Fallflipper_length_mmals einzige unabhängige Variable und als abhängige Variablebody_mass_g - Wie die Folds (
cv) erzeugt werden: in diesem Fall wie viele - also was \(k\) ist - welche Metrik (
scoring): in unserem Fall R² (und zwar out-of-sample) Hier eine Liste aller verfügbaren Scoring-Metriken
Die Funktion gibt uns R²-Werte für jeden Fold zurück und daraus können wir natürlich auch einfach den Mittelwert berechnen.
Wir können das ganze aber auch komplexer gestalten, bzw. mehr Kontrolle übernehmen. So gibt es hier nämlich beispielsweise nicht wie in KFold() das Argument shuffle. Das heißt, dass beim Ausführen der Funktion cross_val_score() die Daten nicht zufällig gemischt werden, sondern in der Reihenfolge bleiben wie sie in X und y vorliegen. Tatsächlich kann man dem cv Argument statt nur einer Zahl aber auch direkt den Output von KFold() übergeben und so eben doch mehr über die Aufteilung der Daten steuern. Und übrigens: Da wir ja einen Wert pro Fold erhalten, können wir diese Werte nicht nur mitteln, sondern auch beispielsweise deren Standardabweichung berechnen, um zu sehen wie stabil unser Modell ist.
model = LinearRegression()
X = gentoo_small[['flipper_length_mm']]
y = gentoo_small['body_mass_g']
cv = KFold(n_splits=5, shuffle=True, random_state=42)
cv_r2 = cross_val_score(model, X, y, cv=cv, scoring='r2')
cv_neg_mae = cross_val_score(model, X, y, cv=cv, scoring='neg_mean_absolute_error')
cv_neg_rmse = cross_val_score(model, X, y, cv=cv, scoring='neg_root_mean_squared_error')
print(f"R² Durchschnitt: {cv_r2.mean():.3f} (±{cv_r2.std():.3f})")
print(f"MAE Durchschnitt: {-cv_neg_mae.mean():.1f} g (±{cv_neg_mae.std():.1f})")
print(f"RMSE Durchschnitt: {-cv_neg_rmse.mean():.1f} g (±{cv_neg_rmse.std():.1f})")R² Durchschnitt: 0.486 (±0.170)
MAE Durchschnitt: 274.3 g (±36.9)
RMSE Durchschnitt: 354.0 g (±60.0)Für noch detailliertere Informationen und Kontrolle können wir von cross_val_score() zu cross_validate() wechseln, um beispielsweise mehrere Metriken gleichzeitig zu berechnen:
model = LinearRegression()
X = gentoo_small[['flipper_length_mm']]
y = gentoo_small['body_mass_g']
cv = KFold(n_splits=5, shuffle=True, random_state=42)
scoring = ['r2', 'neg_mean_absolute_error', 'neg_root_mean_squared_error']
cv_results = cross_validate(
model, X, y,
cv=cv,
scoring=scoring,
return_train_score=True # Auch Training-Scores (In-Sample) zurückgeben
)
# Ergebnisse organisiert anzeigen
results_df = pd.DataFrame({
'Fold': range(1, 6),
'R²_Train': cv_results['train_r2'],
'R²_Test': cv_results['test_r2'],
'MAE_Test': -cv_results['test_neg_mean_absolute_error'],
'RMSE_Test': -cv_results['test_neg_root_mean_squared_error']
})
print(results_df.round(3)) Fold R²_Train R²_Test MAE_Test RMSE_Test
0 1 0.527 0.431 272.874 347.648
1 2 0.491 0.559 286.720 381.102
2 3 0.581 0.181 335.449 452.287
3 4 0.488 0.606 250.535 310.127
4 5 0.477 0.654 225.950 279.033Visualisierung der Cross Validation Variabilität
Die Kreuzvalidierung gibt uns wie gesagt einen Wert je Fold, von denen wir nicht nur einen Durchschnittswert, sondern auch z.B. die Standardabweichung über die verschiedenen Folds berechnen können. Die Werte pro Fold können wir aber auch wie gewohnt z.B. per Boxplot visualisieren:
Code zeigen/verstecken
# Daten für Boxplot vorbereiten
metrics_data = [
cv_results['test_r2'],
-cv_results['test_neg_mean_absolute_error'],
-cv_results['test_neg_root_mean_squared_error']
]
labels = ['R²', 'MAE (g)', 'RMSE (g)']
fig, axes = plt.subplots(1, 3, figsize=(15, 5), layout='tight')
for i, (data, label) in enumerate(zip(metrics_data, labels)):
axes[i].boxplot(data, patch_artist=True,
boxprops=dict(facecolor='lightblue', alpha=0.7));
axes[i].scatter(np.ones(len(data)), data, color='red', alpha=0.8, s=50)
axes[i].set_ylabel(label)
axes[i].set_title(f'{label} über 5 Folds')
axes[i].set_xticks([])
axes[i].grid(True, alpha=0.3)
# Durchschnitt als horizontale Linie
axes[i].axhline(y=data.mean(), color='green', linestyle='--', linewidth=2)
plt.suptitle('Cross Validation: Variabilität der Metriken über Folds')
plt.show()
Betrachtet man die Abbildung genau, sieht man wie verschieden die Metriken über die verschiedenen Folds verteilt sind. Das gibt uns ein Gefühl dafür, wie stabil unser Modell ist und ob es vielleicht in einigen Fällen deutlich schlechter abschneidet als in anderen.
Spezielle Cross Validation Methoden
Stratified K-Fold
Bei Klassifikationsproblemen mit unbalancierten Klassen ist es wichtig, dass jeder Fold eine ähnliche Verteilung der Klassen hat. Dafür gibt es Stratified K-Fold, also eine stratifizierte Version von K-Fold. Dabei wird sichergestellt, dass die Klassenverteilung in jedem Fold der Klassenverteilung im gesamten Datensatz entspricht. Anders ausgedrückt: Auch jeder erzeugte Teildatensatz (Fold) hat prozentual gesehen gleich viele Pinguine pro Art wie der gesamte Datensatz.
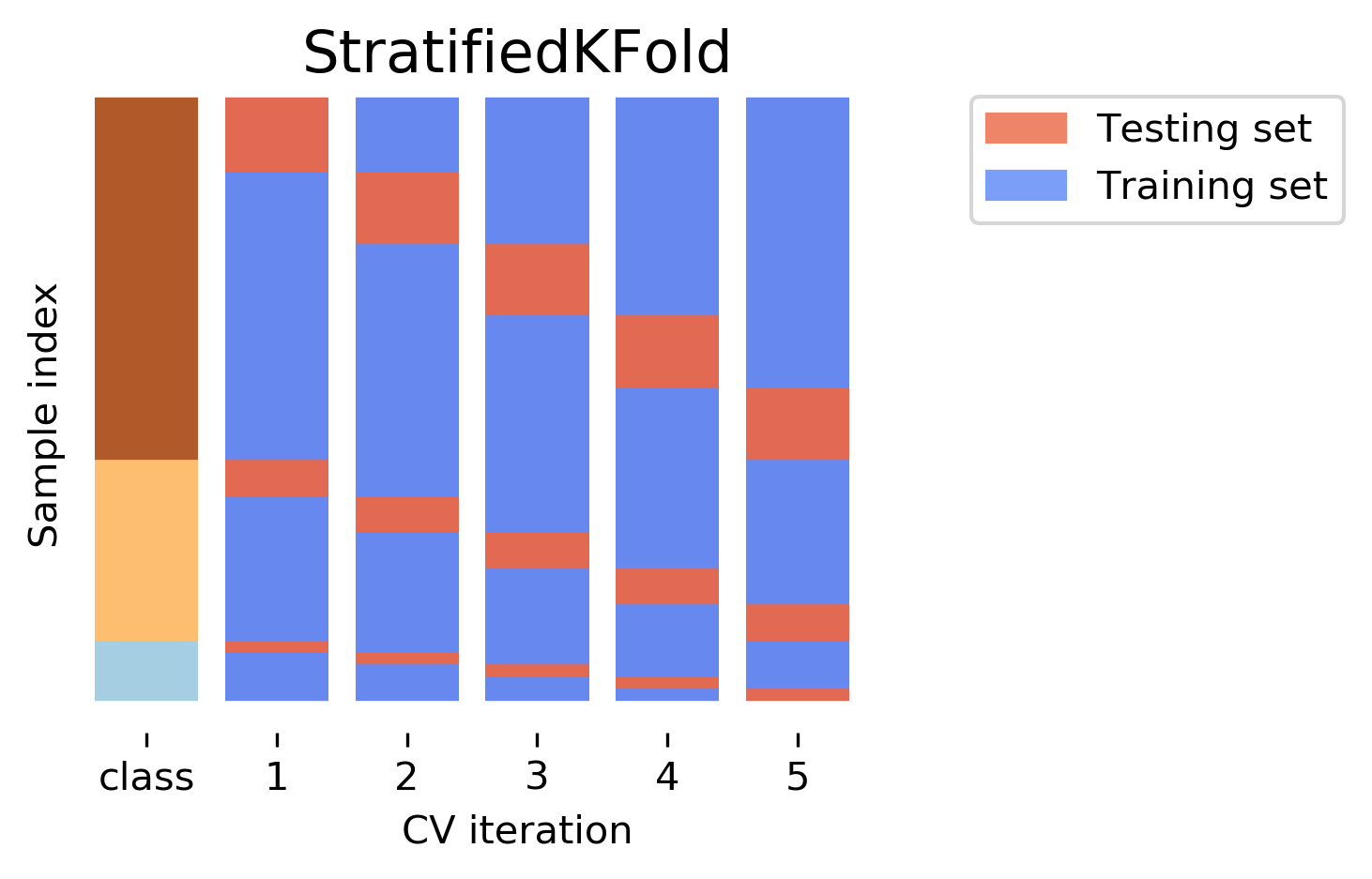
Quelle: Andreas Müller
Gerade bei unseren Pinguin-Daten, wo wir drei Arten mit deutlich unterschiedlichen Anzahlen haben, ist das relevant:
penguins_clean = penguins.dropna()
X_classification = penguins_clean[['flipper_length_mm', 'bill_length_mm']]
y_classification = penguins_clean['species']
print("Klassenverteilung in den gesamten Daten:")
print(y_classification.value_counts())
print(f"Anteile: {y_classification.value_counts(normalize=True).round(3).to_dict()}")Klassenverteilung in den gesamten Daten:
species
Adelie 146
Gentoo 119
Chinstrap 68
Name: count, dtype: int64
Anteile: {'Adelie': 0.438, 'Gentoo': 0.357, 'Chinstrap': 0.204}Das Problem wird klar, wenn wir normale K-Fold mit Stratified K-Fold vergleichen:
from sklearn.model_selection import StratifiedKFold
# Normales K-Fold vs. Stratified K-Fold
normal_kf = KFold(n_splits=5, shuffle=True, random_state=42)
stratified_kf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)Der Unterschied ist dramatisch! Bei normalem K-Fold können manche Folds sehr unbalancierte Test-Sets haben, während Stratified K-Fold eine konsistente Klassenverteilung über alle Folds gewährleistet.
Code zeigen/verstecken
# Daten für Visualisierung sammeln
def get_fold_distributions(cv_method, X, y, method_name):
distributions = []
for fold, (train_idx, test_idx) in enumerate(cv_method.split(X, y) if hasattr(cv_method, 'split') else cv_method.split(X), 1):
test_props = y.iloc[test_idx].value_counts(normalize=True)
for species in ['Adelie', 'Chinstrap', 'Gentoo']:
distributions.append({
'Fold': fold,
'Species': species,
'Proportion': test_props.get(species, 0),
'Method': method_name
})
return pd.DataFrame(distributions)
# Für normales K-Fold - wir müssen y als Parameter übergeben für split(), aber es wird ignoriert
normal_dist = get_fold_distributions(normal_kf, X_classification, y_classification, 'Normal K-Fold')
stratified_dist = get_fold_distributions(stratified_kf, X_classification, y_classification, 'Stratified K-Fold')
# Visualisierung als stacked bar chart
fig, axes = plt.subplots(1, 2, figsize=(15, 6), layout='tight')
# Normal K-Fold
normal_pivot = normal_dist.pivot(index='Fold', columns='Species', values='Proportion')
normal_pivot.plot(kind='bar', stacked=True, ax=axes[0], color=colors)
axes[0].set_title('Normal K-Fold: Unbalancierte Test-Sets')
axes[0].set_ylabel('Anteil im Test-Set')
axes[0].set_xlabel('Fold')
axes[0].legend(title='Species')
axes[0].tick_params(axis='x', rotation=0)
# Stratified K-Fold
stratified_pivot = stratified_dist.pivot(index='Fold', columns='Species', values='Proportion')
stratified_pivot.plot(kind='bar', stacked=True, ax=axes[1], color=colors)
axes[1].set_title('Stratified K-Fold: Balancierte Test-Sets')
axes[1].set_ylabel('Anteil im Test-Set')
axes[1].set_xlabel('Fold')
axes[1].legend(title='Species')
axes[1].tick_params(axis='x', rotation=0)
plt.suptitle('Klassenverteilungen in Test-Sets: Normal vs. Stratified K-Fold')
plt.show()
Warum ist das wichtig? Bei unbalancierten Daten kann es passieren, dass ein Test-Fold sehr wenige oder gar keine Beispiele einer Minderheitsklasse enthält. Das macht die Evaluation unzuverlässig und kann zu irreführenden Metriken führen.
Leave-One-Out Cross Validation
Leave-One-Out (LOO) ist der Extremfall von K-Fold, bei dem k = Anzahl der Datenpunkte. In unserem Fall also ein 100-fold für 100 Datenpunkte: Jeder Punkt wird einmal als Test verwendet, wobei die anderen 99 dann jeweils Trainingsdaten sind. Das ist besonders nützlich bei sehr kleinen Datensätzen, da es sicherstellt, dass jedes einzelne Beispiel als Test verwendet wird.
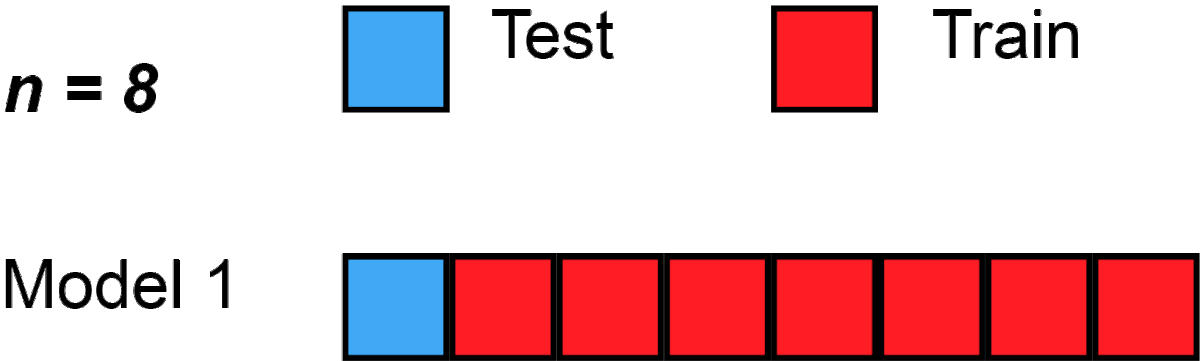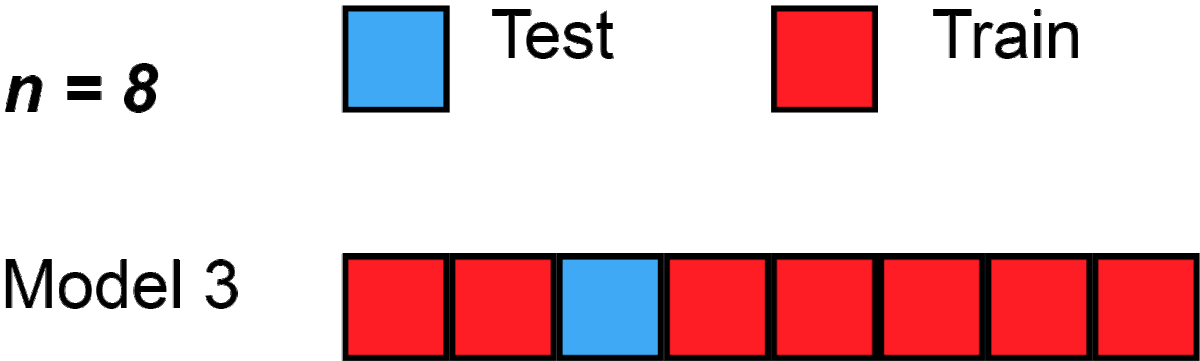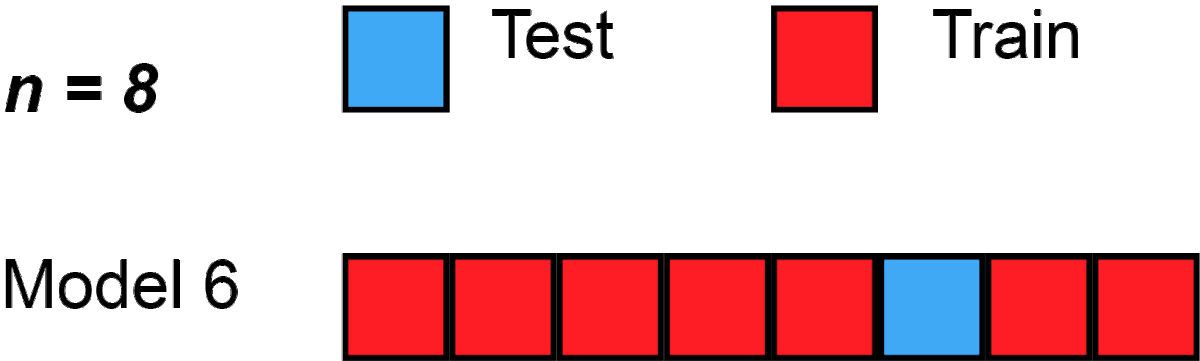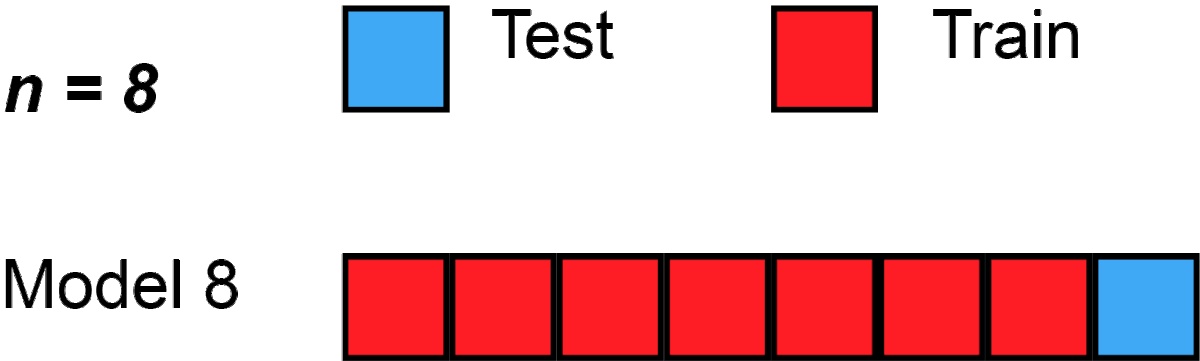
from sklearn.model_selection import LeaveOneOut
# Leave-One-Out Cross Validation mit reduzierter Datenmenge für Memory-Effizienz
# Verwende nur die ersten 30 Datenpunkte statt alle 100
X_small = X[:30]
y_small = y[:30]
loo = LeaveOneOut()
loo_scores = cross_val_score(model, X_small, y_small, cv=loo, scoring='neg_mean_absolute_error')
print(f"Leave-One-Out Cross Validation (reduzierte Datenmenge):")
print(f"Anzahl Datenpunkte: {len(X_small)}")
print(f"Anzahl Folds: {len(loo_scores)}")
print(f"MAE Durchschnitt: {-loo_scores.mean():.1f} g")
print(f"MAE Standardabweichung: {loo_scores.std():.1f} g")
print(f"Vergleich mit 5-Fold CV MAE: {-cv_neg_mae.mean():.1f} g")Leave-One-Out Cross Validation (reduzierte Datenmenge):
Anzahl Datenpunkte: 30
Anzahl Folds: 30
MAE Durchschnitt: 364.0 g
MAE Standardabweichung: 307.2 g
Vergleich mit 5-Fold CV MAE: 274.3 gLOO kann bei kleinen Datensätzen nützlich sein, ist aber rechenintensiv und kann bei größeren Datensätzen instabile Ergebnisse liefern.
Repeated K-Fold Cross Validation
Eine Limitation von normalem K-Fold ist, dass die Ergebnisse noch immer von der spezifischen zufälligen Aufteilung der Daten abhängen. Selbst bei shuffle=True bekommen wir bei jedem random_state etwas andere Ergebnisse. Repeated K-Fold versucht auch dieses Problem zu lösen, indem es noch einen draufsetzt und den K-Fold-Prozess mehrfach mit verschiedenen zufälligen Aufteilungen wiederholt.
Die Grundidee: Statt einmal 5-Fold CV durchzuführen, machen wir beispielsweise 3-mal 5-Fold CV mit jeweils unterschiedlichen zufälligen Splits. Das gibt uns \(k \times \text{repeats}\) Evaluationen - in diesem Fall also 15 statt 5 Werte.
from sklearn.model_selection import RepeatedKFold
# Normales 5-Fold vs. Repeated 5-Fold (3 Wiederholungen)
model = LinearRegression()
X = gentoo_small[['flipper_length_mm']]
y = gentoo_small['body_mass_g']
# Normales 5-Fold
normal_kf = KFold(n_splits=5, shuffle=True, random_state=42)
normal_scores = cross_val_score(model, X, y, cv=normal_kf, scoring='r2')
# Repeated 5-Fold (3 Wiederholungen = insgesamt 15 Evaluationen)
repeated_kf = RepeatedKFold(n_splits=5, n_repeats=3, random_state=42)
repeated_scores = cross_val_score(model, X, y, cv=repeated_kf, scoring='r2')
print(f"Normales 5-Fold CV:")
print(f" Anzahl Scores: {len(normal_scores)}")
print(f" R² Durchschnitt: {normal_scores.mean():.3f} (±{normal_scores.std():.3f})")
print(f"\nRepeated 5-Fold CV (3 Wiederholungen):")
print(f" Anzahl Scores: {len(repeated_scores)}")
print(f" R² Durchschnitt: {repeated_scores.mean():.3f} (±{repeated_scores.std():.3f})")Normales 5-Fold CV:
Anzahl Scores: 5
R² Durchschnitt: 0.486 (±0.170)
Repeated 5-Fold CV (3 Wiederholungen):
Anzahl Scores: 15
R² Durchschnitt: 0.469 (±0.164)Der Hauptvorteil liegt in stabileren und zuverlässigeren Schätzungen der Modell-Performance. Durch die Wiederholungen reduzieren wir die Variabilität, die durch zufällige Splits entstehen kann.
Code zeigen/verstecken
# Visualisierung der Stabilität
fig, axes = plt.subplots(1, 2, figsize=(15, 6), layout='tight')
# Boxplot für normales K-Fold
axes[0].boxplot(normal_scores, patch_artist=True,
boxprops=dict(facecolor='lightblue', alpha=0.7));
axes[0].scatter(np.ones(len(normal_scores)), normal_scores, color='red', alpha=0.8, s=50);
axes[0].set_ylabel('R² Score')
axes[0].set_title('Normales 5-Fold CV')
axes[0].set_xticks([])
axes[0].grid(True, alpha=0.3)
# Boxplot für Repeated K-Fold
axes[1].boxplot(repeated_scores, patch_artist=True,
boxprops=dict(facecolor='lightgreen', alpha=0.7));
axes[1].scatter(np.ones(len(repeated_scores)), repeated_scores, color='red', alpha=0.8, s=50);
axes[1].set_ylabel('R² Score')
axes[1].set_title('Repeated 5-Fold CV (3 Wiederholungen)')
axes[1].set_xticks([])
axes[1].grid(True, alpha=0.3)
plt.suptitle('Stabilität der CV-Scores: Normal vs. Repeated K-Fold')
plt.show()[]
[]
Wann ist Repeated K-Fold sinnvoll?
- Bei kleinen Datensätzen, wo einzelne Splits stark variieren können
- Wenn präzise Performance-Schätzungen wichtig sind (z.B. für Modellvergleiche)
- Bei kritischen Anwendungen, wo Zuverlässigkeit vor Geschwindigkeit geht
Trade-off: Repeated K-Fold braucht mehr Rechenzeit (\(k × repeats\) statt nur \(k\) Modelle), liefert aber stabilere Ergebnisse. In der Praxis ist 3-5 Wiederholungen oft ein guter Kompromiss.
Und übrigens: Ja, es gibt auch einen repeated stratified K-Fold und den nutzen wir auch im folgenden Abschnitt.
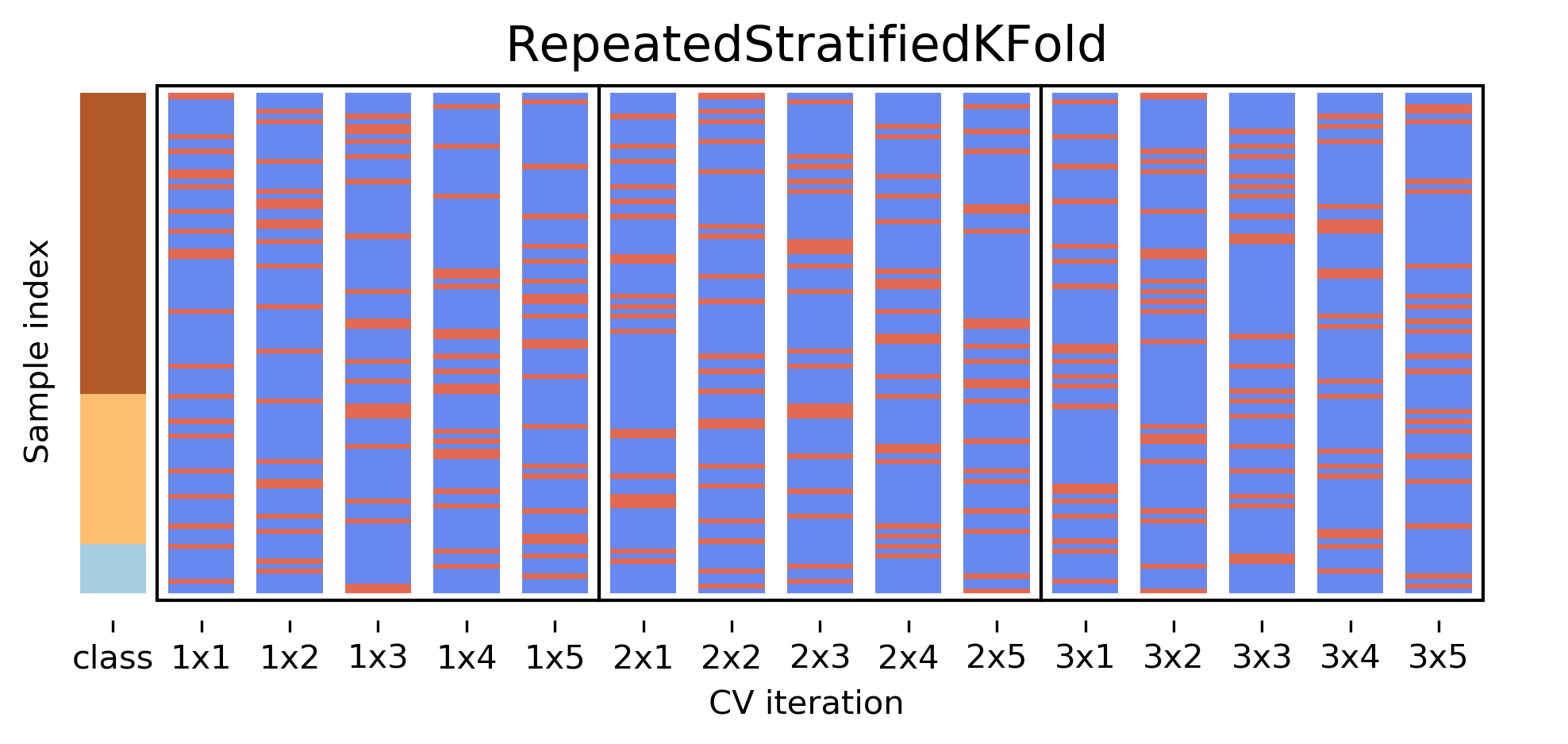
Quelle: Andreas Müller
Praktisches Beispiel: Logistische Regression mit Cross Validation
Zum Abschluss wollen wir mal einen Schritt zurück machen und ein anderes Beispiel ohne Firlefanz durchrechnen. Mit anderen Worten: Wir wollen uns anschauen, wie einfach es ist, eine logistische Regression mit Cross Validation zu evaluieren.
Als Beispiel nehmen wir unsere logistische Regression aus Kapitel 5.1, aber diesmal mit Kreuzvalidierung:
# Notwendige Module importieren
import pandas as pd
import numpy as np
from sklearn.model_selection import StratifiedKFold, cross_validate
from sklearn.linear_model import LogisticRegression
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Daten für binäre Klassifikation vorbereiten
penguins_binary = (
penguins
.loc[penguins['species'].isin(['Gentoo', 'Adelie']), ['species', 'body_mass_g']] # Nur Gentoo und Adelie auswählen
.dropna(subset=['body_mass_g']) # Fehlwerte in body_mass_g entfernen
)
# Binäre Zielvariable erstellen (1 = Gentoo, 0 = Adelie)
penguins_binary['species_binary'] = (penguins_binary['species'] == 'Gentoo').astype(int)
# Logistische Regression mit Stratified Cross Validation
model = LogisticRegression() # Logistisches Regressionsmodell initialisieren
X = penguins_binary[['body_mass_g']] # Unabhängige Variable: Körpergewicht
y = penguins_binary['species_binary'] # Abhängige Variable: Art (binär kodiert)
# Repeated Stratified K-Fold für balancierte Test-Sets verwenden
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=10, random_state=42)
# Cross Validation mit mehreren Metriken durchführen
cv_logreg_results = cross_validate(
model, X, y, # Modell und Daten
cv=cv, # Stratified K-Fold Validierung
scoring=['accuracy', 'precision', 'recall', 'f1', 'roc_auc'], # Klassifikationsmetriken
return_train_score=True # Auch Training-Scores berechnen
)
# Ergebnisse in DataFrame organisieren
results_data = []
for metric in ['accuracy', 'precision', 'recall', 'f1', 'roc_auc']:
test_scores = cv_logreg_results[f'test_{metric}'] # Test-Scores für aktuelle Metrik
results_data.append({
'Metrik': metric.upper(),
'Durchschnitt': test_scores.mean(),
'StdAbw': test_scores.std(),
'Min': test_scores.min(),
'Max': test_scores.max()
})
# DataFrame erstellen und anzeigen
results_df = pd.DataFrame(results_data)
print("Logistische Regression - 5-Fold Stratified Cross Validation:")
print(results_df.round(3))Logistische Regression - 5-Fold Stratified Cross Validation:
Metrik Durchschnitt StdAbw Min Max
0 ACCURACY 0.909 0.036 0.815 0.982
1 PRECISION 0.904 0.044 0.808 1.000
2 RECALL 0.894 0.070 0.720 1.000
3 F1 0.897 0.042 0.783 0.980
4 ROC_AUC 0.979 0.012 0.939 0.997Wie man sieht, sind nur relativ wenige Zeilen Code nötig.
Übungen
In allen der folgenden Aufgaben sollen mehr oder weniger dieselben Daten ausgewertet werden: Wie schon in einer vorangegangenen Übung soll es um die Klassifikation von Pinguinen gehen, diesmal aber um die Unterscheidung zwischen Gentoo und Chinstrap Pinguinen basierend auf Körpergewicht. Die Klassifikations soll mit einer logistischen Regression passieren.
Aufgabe 1: Zeitvergleich verschiedener Cross Validation Methoden
Führe einen Vergleich der Ausführungszeiten verschiedener Cross Validation Methoden durch:
- Leave-One-Out Cross Validation
- Stratified K-Fold mit k=3
- Stratified K-Fold mit k=10
Zeit stoppen in Python: Um die Ausführungszeit zu messen, verwendest du das time Modul:
import time
# Zeit vor dem Code messen
start_time = time.time()
# Hier kommt dein Code (z.B. Cross Validation)
# ...
# Zeit nach dem Code messen
end_time = time.time()
# Differenz berechnen = Ausführungszeit
execution_time = end_time - start_time
print(f"Ausführungszeit: {execution_time:.2f} Sekunden")Deine Aufgabe:
- Implementiere alle drei CV-Methoden und stoppe jeweils die Zeit
- Erstelle einen DataFrame mit zwei Spalten:
-
Methode: Namen der CV-Methoden -
Dauer_Sekunden: Gemessene Ausführungszeiten
-
- Für die Stratified K-Fold Methoden verwende
random_state=42
Aufgabe 2: Repeated Stratified K-Fold Cross Validation
Führe eine umfassende Cross Validation Analyse durch. Diese ist im Prinzip identisch zu dem “Praktischen Beispiel” aus dem letzten Abschnitt, aber eben für die Pinguinarten Gentoo und Chinstrap, sowie dies:
- Verwende Repeated Stratified K-Fold mit
n_splits=10undn_repeats=8 - Berechne die Metriken:
accuracy,precision,recall,f1,roc_auc - Erstelle eine Ergebnisübersicht mit Durchschnitt, Standardabweichung, Minimum und Maximum für jede Metrik
Das Ergebnis soll eine Tabelle sein, die so aussieht:
Metrik Durchschnitt StdAbw Min Max
0 ACCURACY x.xxx x.xxx x.xxx x.xxx
1 PRECISION x.xxx x.xxx x.xxx x.xxx
...Aufgabe 3: Visualisierung der besten und schlechtesten Cross Validation Folds
Erstelle eine Figure mit zwei nebeneinanderliegenden Subplots (bester und schlechtester Fold). Genauer gesagt geht es um die zwei Folds mit den besten und schlechtesten Accuracy Scores, aus den insgesamt 80 Folds, die ja in Aufgabe 2 berechnet wurden. Die Figure soll am Ende so aussehen:
Der Plot ähnelt also stark dem, was wir auch in den letzten Kapiteln schon als Resultat einer einfachen logistischen Regression genutzt haben. Besonders ist jetzt die Darstellung der Testdatenpunkte: Sie sind nicht transparant einfarbig auf 0 oder 1, sondern liegen direkt auf der Modellvorhersagekurve und haben als Füllfarbe ihre tatsächliche Art, als Randfarbe aber die vorhergesagte Art. Das macht es einfach zu erkennen, ob das Modell korrekt oder falsch klassifiziert hat.
Hintergrundinfos: Das cv_results Objekt von cross_validate() enthält zwar die Scores für jeden Fold, aber nicht die Information, welche spezifischen Datenpunkte in welchem Fold als Training bzw. Test verwendet wurden. Um diese Information zu bekommen, müssen wir die Splits manuell reproduzieren.
Starter-Code:
# Accuracy-Scores für alle 80 Folds
accuracy_scores = cv_results['test_accuracy']
# Indices der besten und schlechtesten Accuracy finden
best_fold_idx = np.argmax(accuracy_scores)
worst_fold_idx = np.argmin(accuracy_scores)
print(f"Bester Fold (Index {best_fold_idx}): Accuracy = {accuracy_scores[best_fold_idx]:.3f}")
print(f"Schlechtester Fold (Index {worst_fold_idx}): Accuracy = {accuracy_scores[worst_fold_idx]:.3f}")
# Splits manuell durchführen um Train/Test Indices zu bekommen
cv_splits = list(cv.split(X, y))