import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
np.random.seed(42)Decision Trees
Nachdem wir nun zwei Kapitel lang gelernt haben wie man Klassifikationsergebnisse bewerten und validieren kann, ist es an der Zeit eine neue Klassifikationsmethode kennenzulernen. Nach der logistischen Regression beschäftigen wir uns deshalb in diesem Kapitel mit Decision Trees (Entscheidungsbäume).
Um zu verstehen, wie Decision Trees funktionieren, kann man sich das Spiel “Wer bin ich?” vor Augen führen - beispielsweise aus dieser Szene aus Inglourious Basterds. Das Prinzip: Eine Person bekommt den Namen einer bekannten Persönlichkeit auf eine Karte geschrieben, klebt sich diese auf die Stirn (ohne sie zu sehen) und muss durch Ja/Nein-Fragen erraten, wer sie ist.
Dabei gibt es prinzipiell gute und schlechte Fragen, um schnell zu erraten, wer man ist:
- Schlechte 1. Frage: “Bin ich Harry Potter?” → Ohne jegliches Vorwissen ist es ziemlich unwahrscheinlich, dass ihr eure Persönlichkeit direkt erratet. Stattdessen erhaltet ihr vermutlich ein “Nein”. Bei einem “Nein” wisst ihr aber nur, dass ihr nicht Harry Potter seid, sodass ihr nahezu genau so ahnungslos seid wie vorher und demnach die Frage nicht gut genutzt habt.
- Gute 1. Frage: “Bin ich männlich?” → Egal ob “Ja” oder “Nein”, ihr halbiert grob die Anzahl möglicher Personen.
Eine Frage kann aber auch lauten “Bin ich nach 1900 geboren?” → Hier nutzt ihr eine numerische Variable (Geburtsjahr) und wählt selbständig eine Zahl (1900), die etwa die Hälfte aller verbleibenden Kandidaten ausschließen würde.
Die besten Fragen sind also die, die unabhängig von der Antwort möglichst viele der verbleibenden Persönlichkeiten ausschließen. Decision Trees funktionieren nach demselben Prinzip, mit einem wichtigen Unterschied: Im Spiel gibt es jede zu erratende Persönlichkeit nur einmal, aber in unseren Daten kommen die zu klassifizierenden Kategorien (wie Pinguinarten) mehrfach vor.
Grundkonzepte
Gleich erzeugen wir unseren ersten, wenn auch sehr kleinen Decision Tree für unsere Palmer Pinguine! Der Code ist versteckt, da er und die Ergebnisse nicht sofort verstanden werden müssen, weil wir das alles gleich noch Schritt für Schritt einführen.
Code zeigen/verstecken
# Palmer Penguins Datensatz laden und vorbereiten
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Daten vorbereiten - nur Adelie und Gentoo, wie in Kapitel 052
penguins_clean = penguins[penguins['species'].isin(['Adelie', 'Gentoo'])].copy()
penguins_clean = penguins_clean[['species', 'body_mass_g', 'sex', 'flipper_length_mm', 'bill_length_mm', 'bill_depth_mm']].dropna()
# Einfachster Decision Tree: nur Körpergewicht, maximale Tiefe 1
X_intro = penguins_clean[['body_mass_g']]
y = penguins_clean['species']
tree_intro = DecisionTreeClassifier(max_depth=1, random_state=42)
tree_intro.fit(X_intro, y);
# Tree visualisieren
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
plot_tree(tree_intro,
feature_names=['Körpergewicht (g)'],
class_names=['Adelie', 'Gentoo'],
filled=True,
rounded=True,
ax=ax)
plt.show()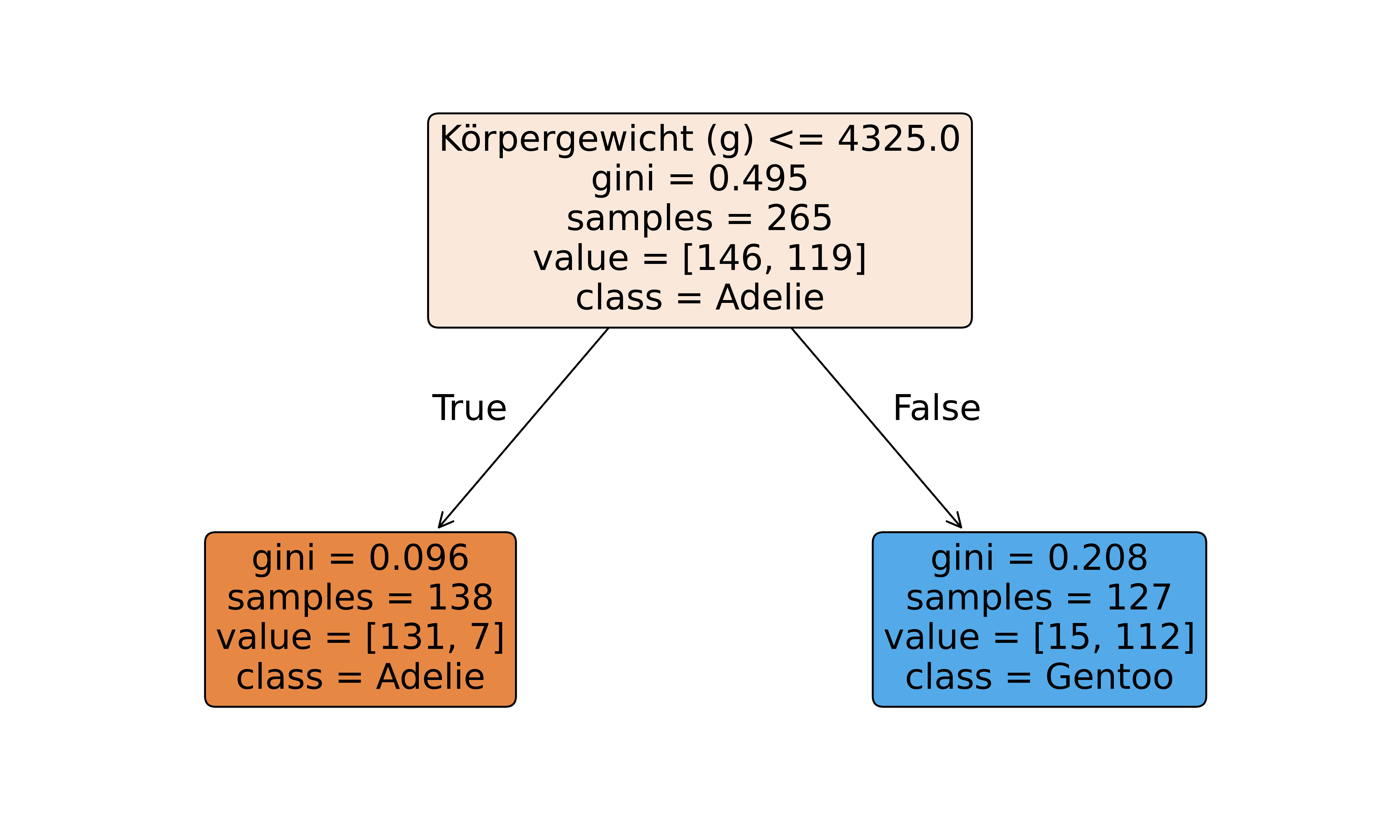
Hier wurde dem Decision-Tree-Algorithmus das Körpergewicht als einzige Variable bereitgestellt und auch nur erlaubt eine einzige “Frage” zu stellen um möglichst gut zu klassifizieren ob ein Pinguin zur Art Adelie oder Gentoo gehört.
Das Resultat: Die beste “Frage” ist “Ist das Körpergewicht ≤ 4325g?” (siehe oberer Rand der oberen Box). Dies teilt die 265 Pinguine (siehe samples Angabe) in zwei Gruppen: Bei 138 ist das der Fall und bei 127 nicht. Nicht nur das: Von den 138 sind 131 Adelie und von den 127 sind 112 Gentoo (siehe value Angabe).
Diese eine einzige Regel klassifiziert also ziemlich gut: “Wenn Körpergewicht ≤ 4325g, dann Adelie, sonst Gentoo.”
Der rekursive Partitionierungs-Algorithmus
Normalerweise - und später in diesem Kapitel - stellt man dem Decision-Tree-Algorithmus mehrere Features zur Verfügung und erlaubt auch mehrere “Fragen”, um die Daten immer weiter zu unterteilen. Das was im Algorithmus dann passiert, ist aber nichts weiter als eine Wiederholung desselben Prinzips, das wir gerade gesehen haben.
Der Algorithmus arbeitet nämlich nach dem Prinzip der rekursiven Partitionierung (recursive partitioning):
- Finde die beste Frage für den aktuellen Datensatz
- Teile die Daten basierend auf der Antwort auf
- Wiederhole den Prozess für jede Teilmenge (falls erlaubt)
- Stoppe, wenn ein Kriterium erfüllt ist (z.B. maximale Tiefe erreicht)
Gerade eben hatten wir die Möglichkeiten des Decision Trees wie gesagt extrem eingeschränkt. Die beste “Frage” konnte nur bzgl. des Körpergewichts gestellt werden und der Prozess durfte nicht wiederholt werden.
Auch wenn wir an dieser Stelle noch nicht verstanden haben wie genau der Algorithmus funktioniert, also wie er entscheidet welches Feature wie aufgeteilt wird um einen gute Partitionierung zu erreichen, so können wir schon jetzt einen Nachteil des Algorithmus verstehen: Der Algorithmus ist greedy (gierig). Das bedeutet, dass bei Decision Trees immer nur die beste Entscheidung für den aktuellen Schritt getroffen wird. In unserem Beispiel oben gibt es nur eine Entscheidung, aber in einem komplexeren Baum würde es mehrere geben. Der Algorithmus schaut aber nicht voraus - tatsächlich weiß der Algorithmus am Anfang sozusagen noch gar nicht wie groß der Baum am Ende wird. Stattdessen trifft immer nur die lokal beste Entscheidung für die aktuelle Situation. Eine solche Partitionierung, die weiter oben im Baum optimal erscheint, könnte langfristig zu einem schlechteren Baum führen als eine “suboptimale” Partitionierung, die bessere nachfolgende Partitionierungen ermöglicht. Diese Eigenschaft macht Decision Trees schnell und effizient, kann aber dazu führen, dass sie nicht den global optimalen Baum finden.
Anatomie eines Decision Trees
Ein fertiger Entscheidungsbaum besteht aus:
- Entscheidungsknoten (Alle Kästen außer den untersten): Stellen eine “Frage” dar (z.B. “Körpergewicht ≤ 4325g?”)
- Blattknoten (die untersten Kästen): Enthalten die finale Klassifikation (z.B. “Adelie”)
- Äste: Verbinden Knoten und repräsentieren die Antworten (links = ja/≤, rechts = nein/>)
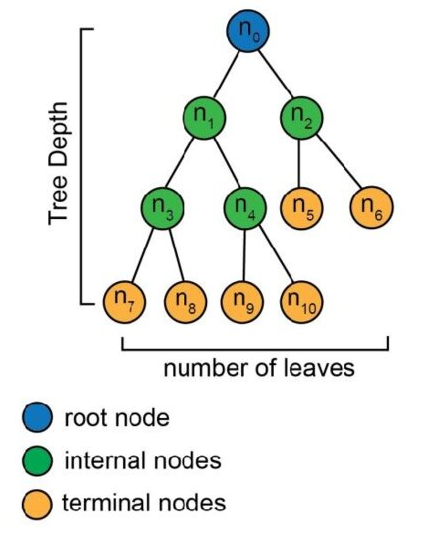
Quelle: Dupont et al. (2020)
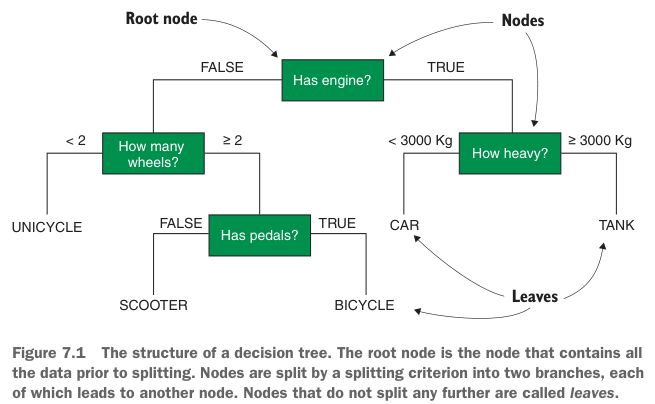
Quelle: Rhys (2020)
Speziell auf die Visualisierung der sklearn Decision Trees bezogen, die wir gerade gesehen haben,gilt:
- Der Baum startet oben (Wurzelknoten) und geht nach unten
- Die Frage steht ganz oben in jedem Knoten (z.B. “body_mass_g ≤ 4325.0”)
- Die Füllfarbe zeigt die Mehrheitsklasse an: Je oranger, desto mehr Adelie; je blauer, desto mehr Gentoo
- Reinere Knoten (fast nur eine Klasse) sind intensiver gefärbt
In jedem Knoten sehen wir auch wichtige Informationen:
- gini: Maß für “Unreinheit” (0 = alle Datenpunkte gehören zur selben Klasse, 0.5 = perfekte Mischung)
- samples: Anzahl der Datenpunkte in diesem Knoten
- value: Exakte Verteilung der Klassen [Adelie, Gentoo]
Splitting-Kriterien: Wie findet der Algorithmus die beste Frage?
Der Algorithmus bewertet jede mögliche Frage anhand des Informationsgewinns:
- Gini-Impurity & Entropy: Messen, wie unrein/unsicher eine Aufteilung ist
- Information Gain: Die Reduktion der Unreinheit/Unsicherheit durch einen Split
Die beste Frage ist die, die die Unsicherheit am stärksten reduziert - genau wie beim “Wer bin ich?”-Spiel!
Gini-Impurity berechnen
Die Gini-Impurity misst, wie “unrein” oder “gemischt” eine Gruppe von Datenpunkten ist. Je gemischter die Klassen, desto höher der Wert:
\[\text{Gini} = 1 - \sum_{i=1}^{k} p_i^2\]
wobei \(p_i\) der Anteil der Klasse \(i\) ist und \(k\) die Anzahl der Klassen. Gini = 0: Perfekt rein (nur eine Klasse); Gini = 0.5: Maximal unrein bei 2 Klassen (50/50 Aufteilung)
Schauen wir uns das für unseren Wurzelknoten an, also den ursprünglichen Datensatz.
# Gini-Impurity manuell berechnen
total = len(penguins_clean)
adelie_count = (penguins_clean['species'] == 'Adelie').sum()
gentoo_count = (penguins_clean['species'] == 'Gentoo').sum()
p_adelie = adelie_count / total
p_gentoo = gentoo_count / total
gini_root = 1 - (p_adelie**2 + p_gentoo**2)
print(f"Wurzelknoten/Urpsrungsdaten:")
print(f" Adelie: {adelie_count} ({p_adelie:.1%})")
print(f" Gentoo: {gentoo_count} ({p_gentoo:.1%})")
print(f" Gini-Impurity: {gini_root:.3f}")Wurzelknoten/Urpsrungsdaten:
Adelie: 146 (55.1%)
Gentoo: 119 (44.9%)
Gini-Impurity: 0.495Unser Wert von ~0.498 zeigt eine fast gleichmäßige Verteilung. Das ist auch zu erwarten, da wir nur zwei Arten haben und beide etwa gleich häufig in den Daten vorkommen.
Entropy
Neben Gini-Impurity gibt es noch ein anderes häufig verwendetes Maß: Entropy (Entropie). Die Formel lautet:
\[\text{Entropy} = -\sum_{i=1}^{k} p_i \log_2(p_i)\]
Berechnen wir Entropy für unseren Wurzelknoten:
# Entropy manuell berechnen
import math
entropy_root = -(p_adelie * math.log2(p_adelie) + p_gentoo * math.log2(p_gentoo))
print(f"Entropy für Wurzelknoten: {entropy_root:.3f}")
print(f"Gini für Vergleich: {gini_root:.3f}")
# Vergleich über verschiedene Mischungsverhältnisse
ratios = np.linspace(0.01, 0.99, 100)
gini_values = [1 - (p**2 + (1-p)**2) for p in ratios]
entropy_values = [-(p * math.log2(p) + (1-p) * math.log2(1-p)) for p in ratios]
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
ax.plot(ratios, gini_values, label='Gini-Impurity', linewidth=2)
ax.plot(ratios, entropy_values, label='Entropy', linewidth=2)
ax.set_xlabel('Anteil Klasse 1')
ax.set_ylabel('Impurity-Maß')
ax.set_title('Vergleich: Gini-Impurity vs. Entropy')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()Entropy für Wurzelknoten: 0.992
Gini für Vergleich: 0.495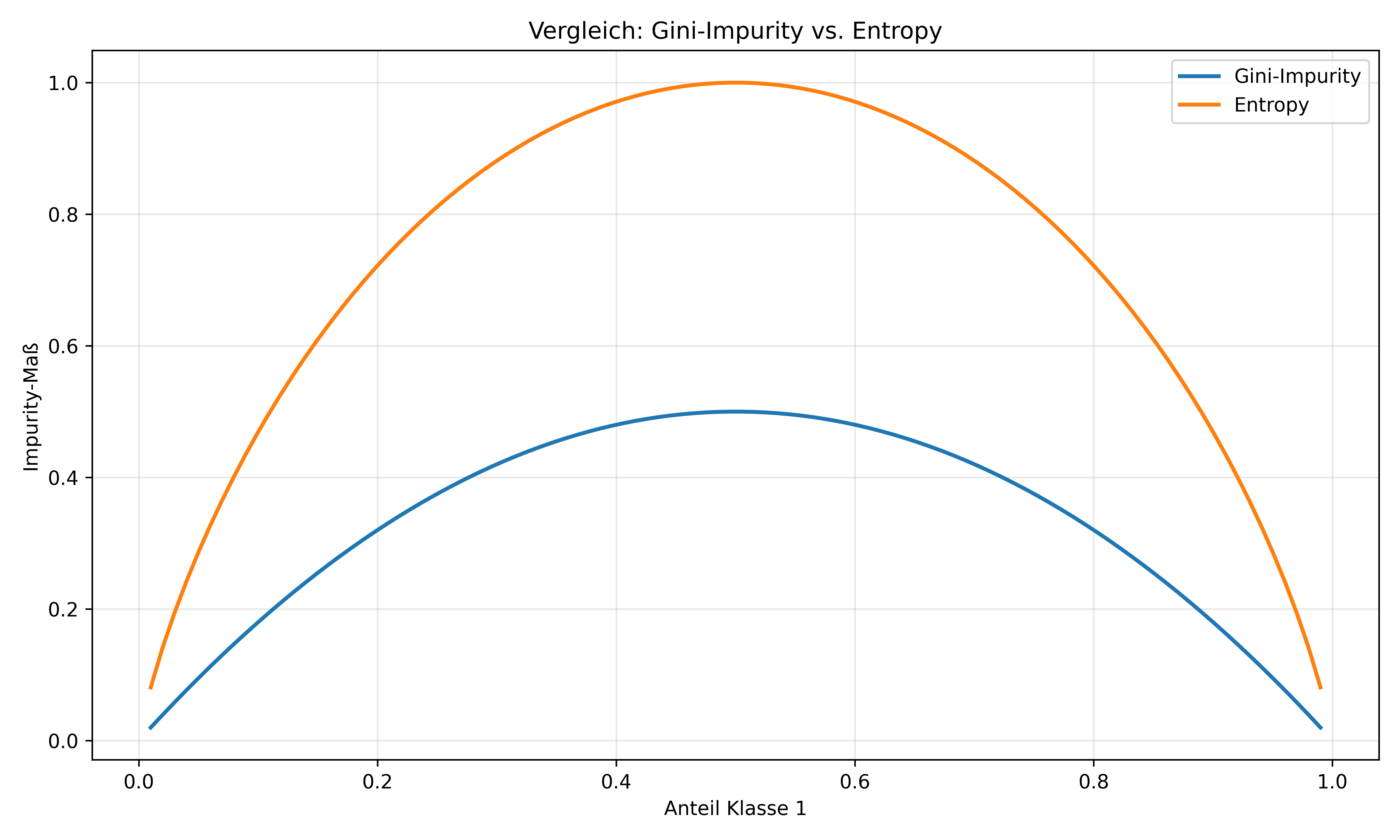
Beide Maße haben ähnliche Eigenschaften, aber Entropy hat eine etwas stärkere “Bestrafung” von Unreinheit. In der Praxis führen beide meist zu sehr ähnlichen Bäumen, wobei Gini etwas schneller zu berechnen ist und daher der sklearn-Standard.
Information Gain berechnen
Der Information Gain misst, wie sehr ein Split die Unsicherheit reduziert:
\[\text{Information Gain} = \text{Gini}_{\text{parent}} - \sum_{j} \frac{n_j}{n} \cdot \text{Gini}_j\]
wobei:
- \(\text{Gini}_{\text{parent}}\) die Unreinheit vor dem Split ist
- \(n_j\) die Anzahl Datenpunkte im Kind-Knoten \(j\)
- \(n\) die Gesamtzahl Datenpunkte
- \(\text{Gini}_j\) die Unreinheit des Kind-Knotens \(j\)
Einfach ausgedrückt: Wir vergleichen Gini-Impurity vor und nach einem Split. Da wir davor nur eine Gini-Impurity haben, danach ja aber zwei, berechnen wir den gewichteten Mittelwert der beiden danach.
Berechnen wir den Information Gain für unseren Split bei 4325g manuell:
# Split bei 4325g durchführen
split_value = 4325
left_mask = penguins_clean['body_mass_g'] <= split_value
right_mask = ~left_mask
# Linker Knoten (≤ 4325g)
left_data = penguins_clean[left_mask]
left_adelie = (left_data['species'] == 'Adelie').sum()
left_gentoo = (left_data['species'] == 'Gentoo').sum()
left_total = len(left_data)
p_left_adelie = left_adelie / left_total
p_left_gentoo = left_gentoo / left_total
gini_left = 1 - (p_left_adelie**2 + p_left_gentoo**2)
# Rechter Knoten (> 4325g)
right_data = penguins_clean[right_mask]
right_adelie = (right_data['species'] == 'Adelie').sum()
right_gentoo = (right_data['species'] == 'Gentoo').sum()
right_total = len(right_data)
p_right_adelie = right_adelie / right_total
p_right_gentoo = right_gentoo / right_total
gini_right = 1 - (p_right_adelie**2 + p_right_gentoo**2)
# Gewichteter Durchschnitt der Kind-Knoten
weighted_gini = (left_total/total) * gini_left + (right_total/total) * gini_right
# Information Gain
info_gain = gini_root - weighted_gini
print(f"\nLinker Knoten (≤ {split_value}g):")
print(f" Adelie: {left_adelie}, Gentoo: {left_gentoo}")
print(f" Gini: {gini_left:.3f}")
print(f"\nRechter Knoten (> {split_value}g):")
print(f" Adelie: {right_adelie}, Gentoo: {right_gentoo}")
print(f" Gini: {gini_right:.3f}")
print(f"\nInformation Gain: {gini_root:.3f} - {weighted_gini:.3f} = {info_gain:.3f}")
Linker Knoten (≤ 4325g):
Adelie: 131, Gentoo: 7
Gini: 0.096
Rechter Knoten (> 4325g):
Adelie: 15, Gentoo: 112
Gini: 0.208
Information Gain: 0.495 - 0.150 = 0.345Der Algorithmus testet ALLE möglichen Splits:
- Für jedes numerische Feature: jeden1 möglichen Schwellenwert
- Für jedes kategorische Feature: jede mögliche Aufteilung
- Wählt den Split mit dem höchsten Information Gain
Visualisieren wir, wie sich der Information Gain für verschiedene Split-Punkte beim Körpergewicht verhält:
Code zeigen/verstecken
# Information Gain für verschiedene Split-Punkte berechnen (sklearn-kompatibel)
unique_weights = sorted(penguins_clean['body_mass_g'].unique())
weights = [(unique_weights[i] + unique_weights[i + 1]) / 2 for i in range(len(unique_weights) - 1)]
info_gains = []
for weight in weights:
# Split durchführen
left = penguins_clean[penguins_clean['body_mass_g'] <= weight]
right = penguins_clean[penguins_clean['body_mass_g'] > weight]
# Gini für beide Seiten
if len(left) > 0 and len(right) > 0:
gini_l = 1 - sum((left['species'].value_counts() / len(left))**2)
gini_r = 1 - sum((right['species'].value_counts() / len(right))**2)
# Gewichteter Durchschnitt
weighted = (len(left)/total) * gini_l + (len(right)/total) * gini_r
info_gains.append(gini_root - weighted)
else:
info_gains.append(0)
# Beste Split-Punkte finden
best_idx = np.argmax(info_gains)
best_weight = weights[best_idx]
best_gain = info_gains[best_idx]
# Visualisierung
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
ax.plot(weights, info_gains, 'b-', alpha=0.7)
ax.scatter(best_weight, best_gain, color='red', s=100, zorder=5)
ax.axvline(best_weight, color='red', linestyle='--', alpha=0.5)
ax.set_xlabel('Split-Punkt (Körpergewicht in g)')
ax.set_ylabel('Information Gain')
ax.set_title('Information Gain für verschiedene Split-Punkte')
ax.text(best_weight, best_gain + 0.01, f'{best_weight}g\nGain: {best_gain:.3f}',
ha='center', va='bottom', bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5))
ax.grid(True, alpha=0.3)
ax.set_ylim(0, 0.4);
plt.show()
print(f"Bester Split: {best_weight}g mit Information Gain von {best_gain:.3f}")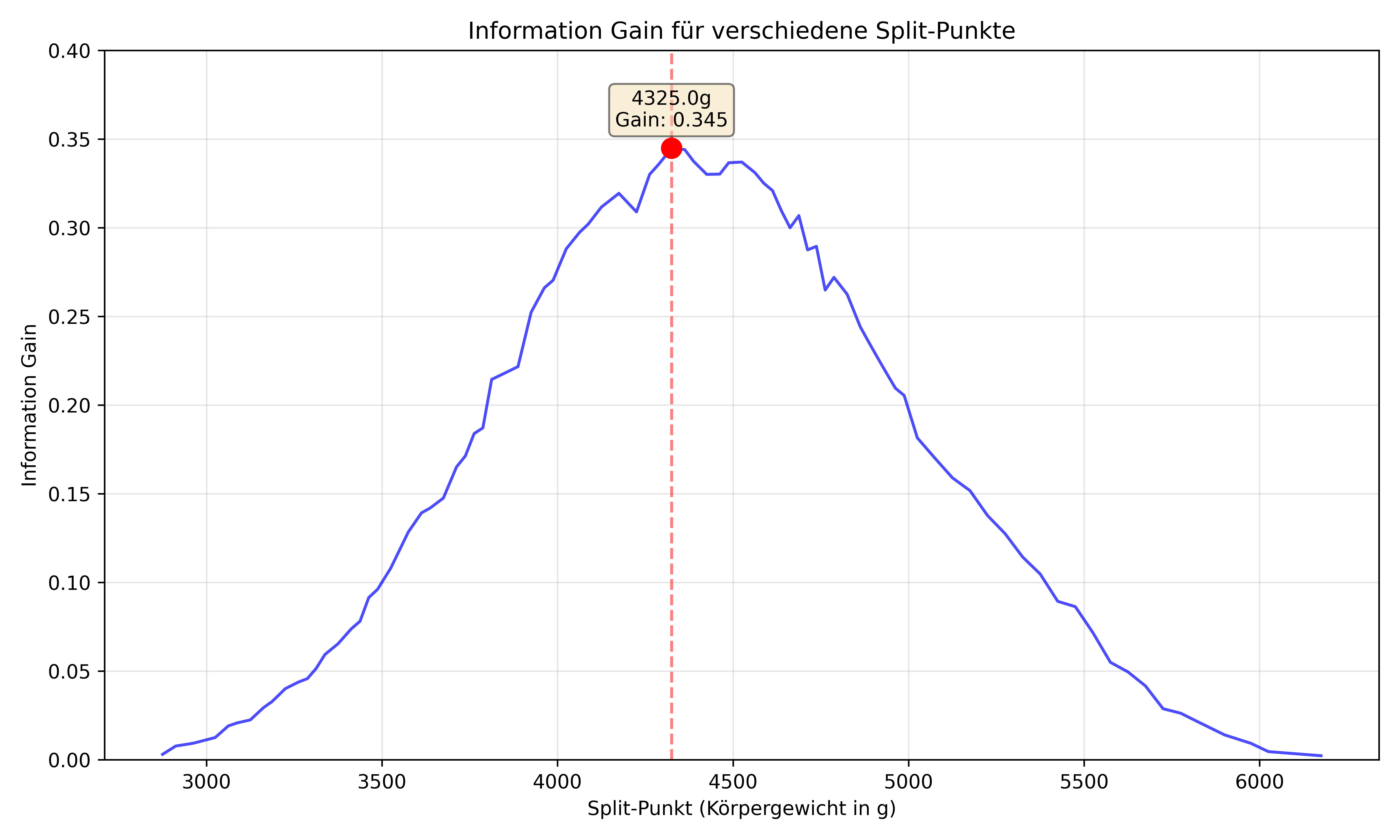
Bester Split: 4325.0g mit Information Gain von 0.345- Der Information Gain hat ein Maximum bei ~4325g
- Links und rechts davon fällt er stark ab
- Bei extremen Werten (sehr kleine/große Splits) geht er gegen 0
Das ist der Kern von Decision Trees: Sie finden automatisch die optimalen Schwellenwerte, die die Daten am besten trennen! Hier haben wir das für eine einzige Variable (Körpergewicht) gesehen, aber der Algorithmus kann das für alle Features gleichzeitig tun.
Umgang mit kategorischen Features
Decision Trees haben einen konzeptionellen Vorteil beim Umgang mit kategorischen Features, aber sklearn benötigt auch hier wieder numerische Kodierung.
Code zeigen/verstecken
# Beispiel mit kategorischem Feature: Geschlecht
# In sklearn müssen wir kategorische Features encodieren
penguins_encoded = penguins_clean.copy()
penguins_encoded['sex_encoded'] = penguins_encoded['sex'].map({'male': 1, 'female': 0})
# Tree mit kategorischem Feature
X_categorical = penguins_encoded[['sex_encoded']] # Encodiertes Geschlecht
tree_cat = DecisionTreeClassifier(max_depth=1, random_state=42)
tree_cat.fit(X_categorical, y);
# Geschlecht-Aufteilung anschauen
print("Aufteilung nach Geschlecht:")
gender_species = pd.crosstab(penguins_clean['sex'], penguins_clean['species'])
print(gender_species)
# Information Gain berechnen
print(f"\nInformation Gain durch Geschlecht-Split:")
males = penguins_clean[penguins_clean['sex'] == 'male']
females = penguins_clean[penguins_clean['sex'] == 'female']
# Gini für männliche Pinguine
male_props = males['species'].value_counts() / len(males)
gini_male = 1 - sum(male_props**2)
# Gini für weibliche Pinguine
female_props = females['species'].value_counts() / len(females)
gini_female = 1 - sum(female_props**2)
# Gewichteter Durchschnitt
weighted_gender = (len(males)/total) * gini_male + (len(females)/total) * gini_female
info_gain_gender = gini_root - weighted_gender
print(f"Information Gain durch Geschlecht: {info_gain_gender:.3f}")
print(f"Zum Vergleich - durch Körpergewicht: {best_gain:.3f}")
# Baum visualisieren
fig, ax = plt.subplots(figsize=(12, 8), layout='tight')
plot_tree(tree_cat,
feature_names=['Geschlecht'],
class_names=['Adelie', 'Gentoo'],
filled=True,
rounded=True,
ax=ax)
ax.set_title('Decision Tree: Nur Geschlecht (female=0, male=1)')
plt.show()Aufteilung nach Geschlecht:
species Adelie Gentoo
sex
female 73 58
male 73 61
Information Gain durch Geschlecht-Split:
Information Gain durch Geschlecht: 0.000
Zum Vergleich - durch Körpergewicht: 0.345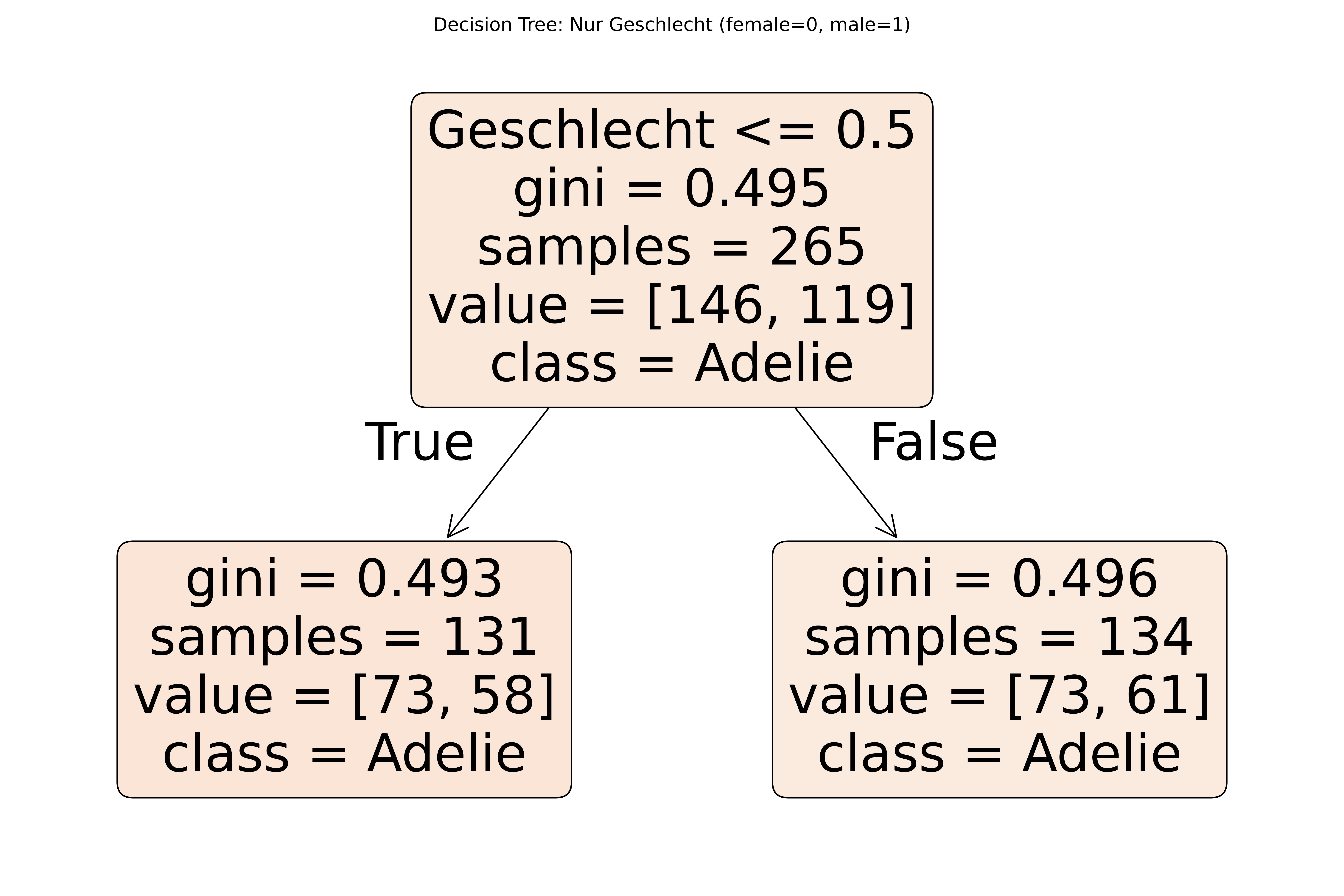
Schrittweise Implementierung
Schritt 1: Der einfachste Decision Tree
Schauen wir uns nun nochmal - aber genauer - das erste Beispiel von oben an: nur ein Feature (Körpergewicht) und nur ein Split. Da wir wieder sklearn nutzen, fällt uns die Syntax recht leicht: Wir tauschen hauptsächlich nur LogisticRegression gegen DecisionTreeClassifier aus. Innerhalb der Funktion haben wir dann aber natürlich auch andere Argumente (siehe Dokumentation). Hier nutzen wir max_depth=1, um nur einen Split zu erlauben und außerdem random_state=42, um die Reproduzierbarkeit zu gewährleisten2.
Da wir diesen Decision Tree schon zum Zweiten mal sehen, habe ich hier probeweise bei plot_tree() noch die Argumente node_ids und proportion auf True gesetzt um zu zeigen, dass man die Visualisierung noch weiter anpassen kann (siehe Dokumentation).
# Nur Körpergewicht verwenden
X_weight_only = penguins_clean[['body_mass_g']]
y = penguins_clean['species']
# Sehr einfacher Decision Tree
tree_simple = DecisionTreeClassifier(max_depth=1, random_state=42)
tree_simple.fit(X_weight_only, y);
# Visualisierung
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
plot_tree(tree_simple,
feature_names=['Körpergewicht (g)'],
class_names=['Adelie', 'Gentoo'],
filled=True,
node_ids=True,
proportion=True,
rounded=True,
ax=ax)
ax.set_title('Decision Tree: Nur Körpergewicht (max_depth=1)')
plt.show()
print(f"Split-Punkt: {tree_simple.tree_.threshold[0]:.1f}g")
print(f"Genauigkeit: {tree_simple.score(X_weight_only, y):.1%}")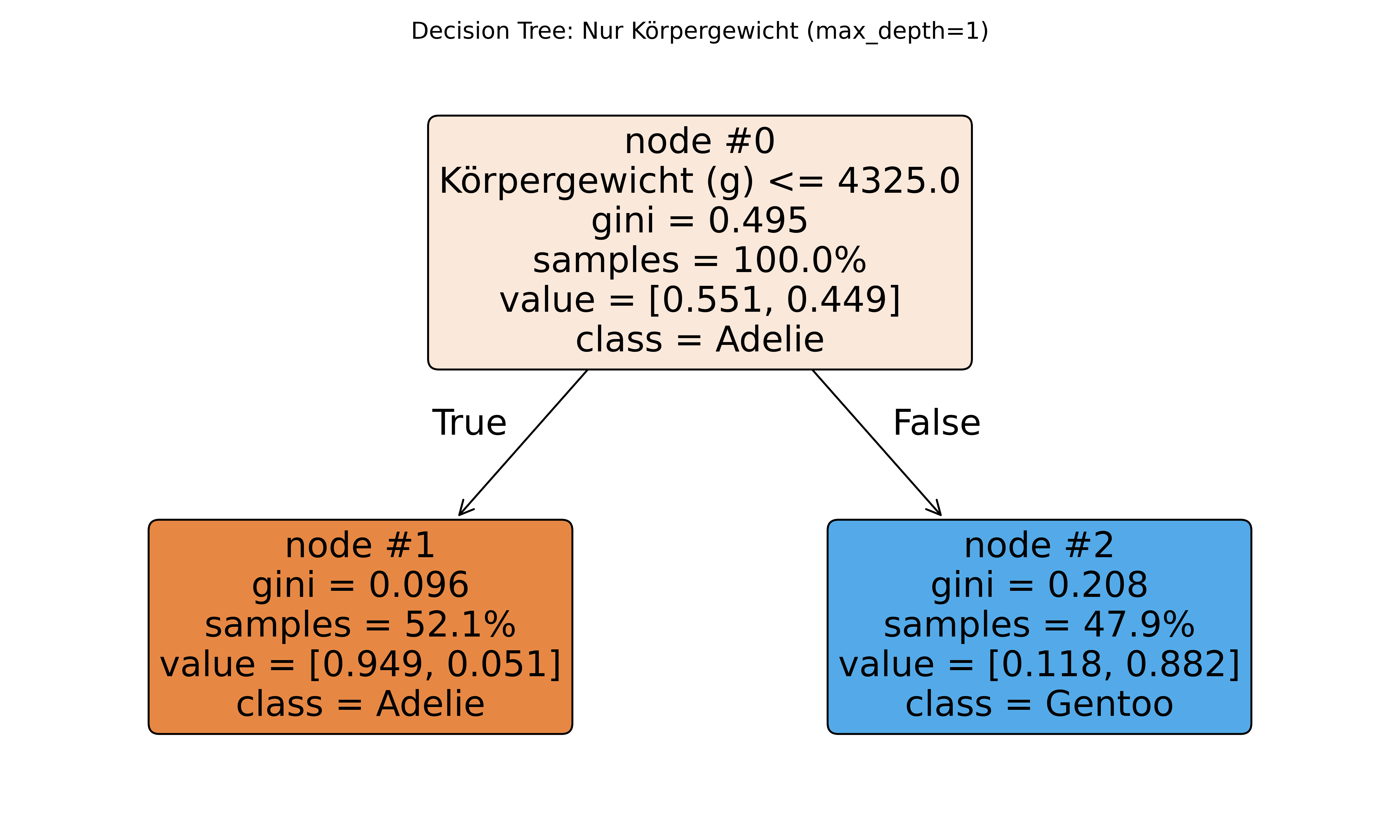
Split-Punkt: 4325.0g
Genauigkeit: 91.7%Vergleich mit logistischer Regression
Damit wir hier nicht den Fokus verlieren wollen wir kurz einen Schritt zurück machen und mit der logistischen Regression vergleichen. Tatsächlich haben wir ja in Kapitel 5.1 genau dieses Beispiel (= Körpergewicht als einzige Variable um zwischen Adelie und Gentoo zu klassifizieren) mit logistischer Regression behandelt. Wir versuchen also anhand einer möglichst vergleichbaren Visualisierung zu zeigen, wie sich die beiden Methoden unterscheiden:
Code zeigen/verstecken
# Für den Vergleich: logistische Regression trainieren
from sklearn.linear_model import LogisticRegression
# Logistische Regression
logreg = LogisticRegression(random_state=42)
logreg.fit(X_weight_only, y);
# Berechne das Gewicht bei p=0.5 für die logistische Regression
# Für binäre logistische Regression: p = 0.5 wenn logit = 0
# logit = intercept + coef * weight = 0
# weight = -intercept / coef
threshold_weight_logr = -logreg.intercept_[0] / logreg.coef_[0][0]
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6), layout='tight')
# Daten für beide Plots
adelie_data = penguins_clean[penguins_clean['species'] == 'Adelie']
gentoo_data = penguins_clean[penguins_clean['species'] == 'Gentoo']
# Plot 1: Logistische Regression
adelie_y = np.zeros(len(adelie_data)) # Adelie = 0
gentoo_y = np.ones(len(gentoo_data)) # Gentoo = 1
ax1.scatter(adelie_data['body_mass_g'], adelie_y, alpha=0.6, color='#FF8C00',
label='Adelie', s=50)
ax1.scatter(gentoo_data['body_mass_g'], gentoo_y, alpha=0.6, color='#159090',
label='Gentoo', s=50)
# Logistische Kurve
x_range = np.linspace(penguins_clean['body_mass_g'].min(),
penguins_clean['body_mass_g'].max(), 200)
X_range = x_range.reshape(-1, 1)
probs = logreg.predict_proba(X_range)[:, 1] # Wahrscheinlichkeit für Gentoo
ax1.plot(x_range, probs, 'red', linewidth=3, label='Logistische Regression')
ax1.axhline(y=0.5, color='gray', linestyle='--', alpha=0.7, label='50%-Schwelle')
ax1.axvline(x=threshold_weight_logr, color='magenta', linestyle='-', linewidth=2,
label=f'Entscheidungsgrenze ({threshold_weight_logr:.0f}g)')
ax1.set_xlabel('Körpergewicht (g)')
ax1.set_ylabel('Wahrscheinlichkeit P(Gentoo)')
ax1.set_title('Logistische Regression\n(Graduelle Wahrscheinlichkeitsschätzung)')
ax1.legend()
ax1.grid(True, alpha=0.3)
# Plot 2: Decision Tree
ax2.scatter(adelie_data['body_mass_g'], adelie_y, alpha=0.6, color='#FF8C00',
label='Adelie', s=50)
ax2.scatter(gentoo_data['body_mass_g'], gentoo_y, alpha=0.6, color='#159090',
label='Gentoo', s=50)
# Decision Tree "Funktion" (Stufenfunktion)
split_point = 4325.0
weights_left = x_range[x_range <= split_point]
weights_right = x_range[x_range > split_point]
# Konstante Wahrscheinlichkeiten basierend auf Mehrheitsklasse
# Links: 131 Adelie, 7 Gentoo → P(Gentoo) = 7/138 ≈ 0.05
# Rechts: 15 Adelie, 112 Gentoo → P(Gentoo) = 112/127 ≈ 0.88
prob_left = 7/138
prob_right = 112/127
ax2.plot(weights_left, [prob_left] * len(weights_left), 'blue', linewidth=3,
label='Decision Tree')
ax2.plot(weights_right, [prob_right] * len(weights_right), 'blue', linewidth=3)
# Vertikale Linie bei Split-Punkt
ax2.axvline(x=split_point, color='magenta', linestyle='-', linewidth=2,
label=f'Split-Punkt ({split_point:.0f}g)')
ax2.set_xlabel('Körpergewicht (g)')
ax2.set_ylabel('Wahrscheinlichkeit P(Gentoo)')
ax2.set_title('Decision Tree\n(Diskrete Wenn-Dann-Regel)')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.show()
print(f"Logistische Regression: Entscheidungsgrenze bei {threshold_weight_logr:.0f}g")
print(f"Decision Tree: Split-Punkt bei {split_point:.0f}g")
Logistische Regression: Entscheidungsgrenze bei 4422g
Decision Tree: Split-Punkt bei 4325gDiese Visualisierung zeigt die fundamentalen Unterschiede zwischen beiden Ansätzen:
Logistische Regression (links) modelliert glatte Übergänge: Die S-förmige Kurve zeigt graduelle Wahrscheinlichkeitsveränderungen. Ein Pinguin mit 4000g hat eine geringe, aber nicht null Wahrscheinlichkeit ein Gentoo zu sein, während ein Pinguin mit 4500g eine mittlere Wahrscheinlichkeit hat.
Decision Tree (rechts) erstellt harte Regeln: “Wenn Körpergewicht ≤ 4325g, dann mit 5% Wahrscheinlichkeit Gentoo, sonst mit 88% Wahrscheinlichkeit Gentoo.” Diese Stufenfunktion ist mathematisch einfacher zu interpretieren, aber weniger flexibel bei graduellen Übergängen.
Beide Methoden können als Klassifikationsmethoden bezeichnet werden und identifizieren ähnliche Schwellenwerte, aber ihre Philosophien sind grundverschieden: graduelle Wahrscheinlichkeitsschätzung versus diskrete Wenn-Dann-Regeln. Ein großer Vorteil der Decision Trees ist ihre hervorragende Interpretierbarkeit: Jeder Pfad im Baum ist eine verständliche Wenn-Dann-Regel, die auch für Nicht-Statistiker leicht nachzuvollziehen ist.
Schritt 2: Tieferer Baum für komplexere Regeln
So weit, so gut! Nun wollen wir aber mal einen tieferen Baum erzeugen. Wir setzen aber vorerst nur max_depth=2 und schauen uns an, was passiert. Wir nutzen erstmal wieder nur das Körpergewicht als Feature.
# Tieferer Baum mit demselben Feature
tree_deeper = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_deeper.fit(X_weight_only, y);
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
plot_tree(tree_deeper,
feature_names=['Körpergewicht (g)'],
class_names=['Adelie', 'Gentoo'],
filled=True,
node_ids=True,
proportion=True,
rounded=True,
ax=ax)
ax.set_title('Decision Tree: Nur Körpergewicht (max_depth=2)')
plt.show()
print(f"Genauigkeit max_depth=1: {tree_simple.score(X_weight_only, y):.1%}")
print(f"Genauigkeit max_depth=2: {tree_deeper.score(X_weight_only, y):.1%}")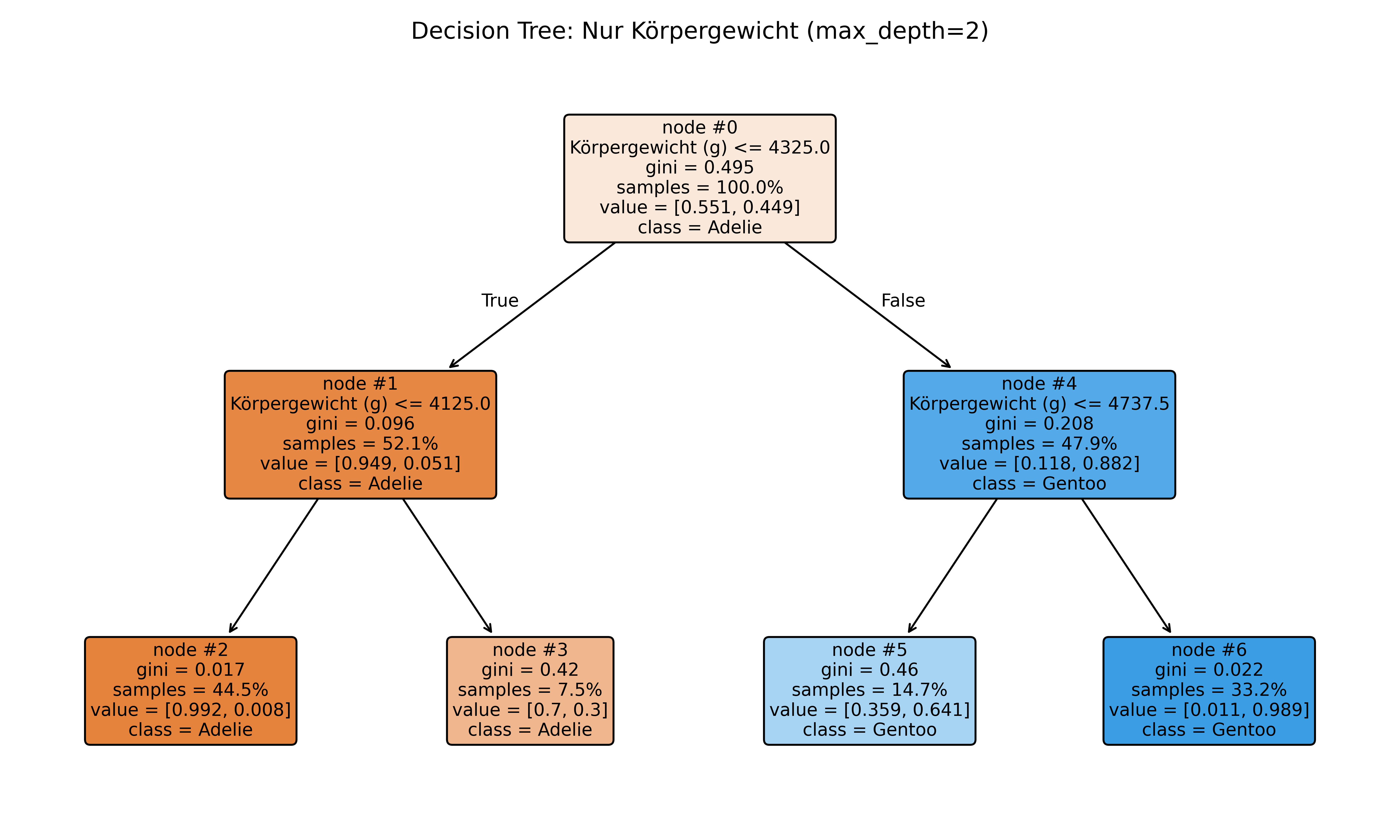
Genauigkeit max_depth=1: 91.7%
Genauigkeit max_depth=2: 91.7%Der tiefere Baum macht zusätzliche Splits bei 4125g und 4737.5g, aber die Genauigkeit bleibt gleich! Die zusätzlichen Regeln verbessern die Vorhersage nicht - das erste einfache Modell war bereits optimal für dieses Feature. Das ist eigentlich auch selbstverständlich, da wir nur ein Feature und nur zwei Pinguinarten haben, sodass der Algorithmus nicht mehr Informationen aus den Daten ziehen kann.
Schritt 3: Mehrere Features hinzufügen
Jetzt der interessante Teil: Was passiert, wenn wir alle verfügbaren Penguin-Features anbieten und maximal 3 Splits erlauben?
# Geschlecht muss numerisch kodiert werden für sklearn
penguins_encoded = penguins_clean.copy()
penguins_encoded['sex_encoded'] = penguins_encoded['sex'].map({'male': 1, 'female': 0})
# Alle Features verwenden
X_all = penguins_encoded[['body_mass_g', 'sex_encoded', 'flipper_length_mm', 'bill_length_mm', 'bill_depth_mm']]
tree_all = DecisionTreeClassifier(max_depth=3, random_state=42)
tree_all.fit(X_all, y);
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
plot_tree(tree_all,
feature_names=['Körpergewicht', 'Geschlecht', 'Flügellänge', 'Schnabellänge', 'Schnabeltiefe'],
class_names=['Adelie', 'Gentoo'],
filled=True,
node_ids=True,
rounded=True,
fontsize=10,
ax=ax)
ax.set_title('Decision Tree: Alle Features')
plt.show()
print(f"Genauigkeit: {tree_all.score(X_all, y):.1%}")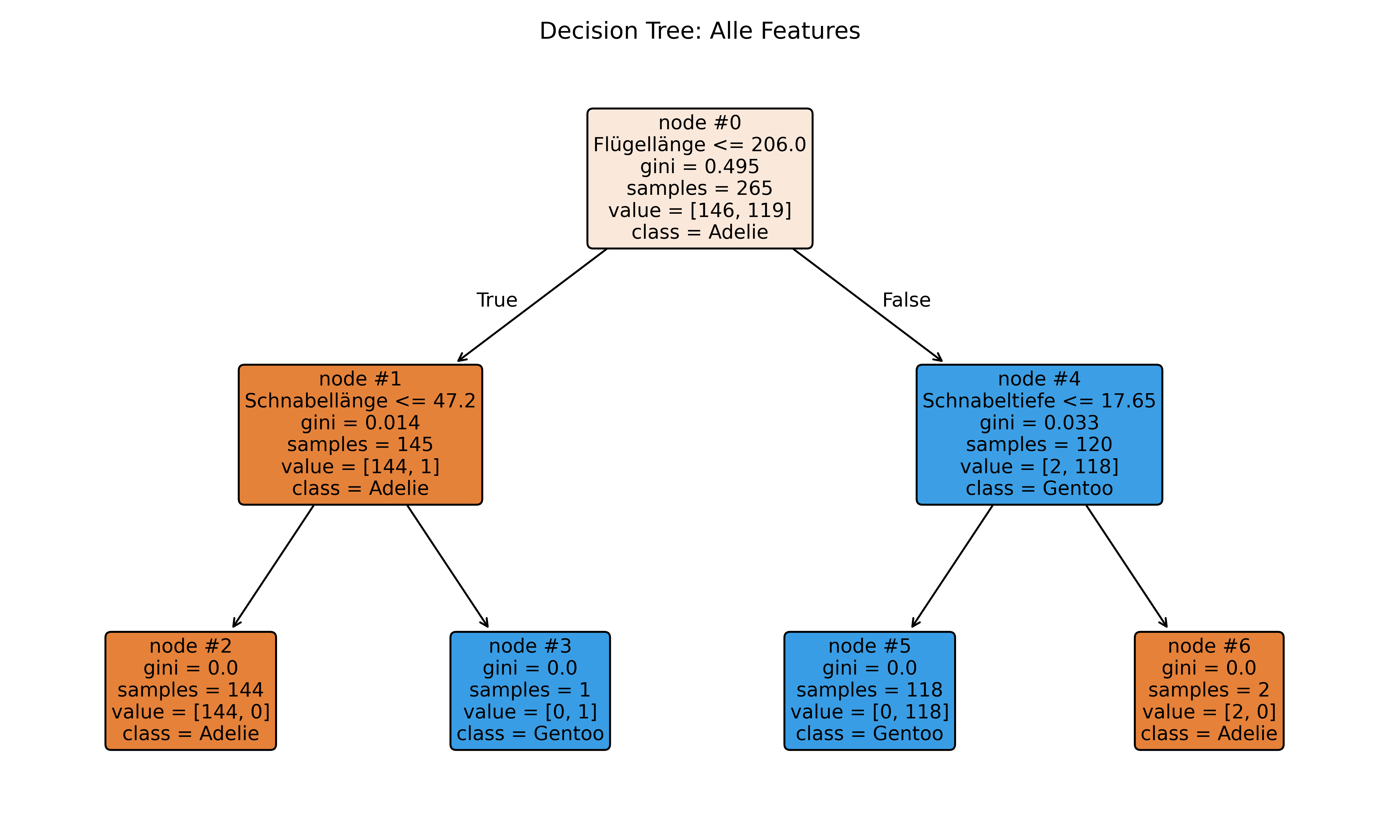
Genauigkeit: 100.0%Beim Betrachten des Ergebnisses sehen wir mehrere Dinge:
- Flügellänge wurde hier für den ersten Split gewählt und beim Betrachten der Gini-Impurity oder Verteilung (value) sehen wir, dass dieser Split die Daten sehr gut trennt - auf jeden Fall besser als der oben mit Körpergewicht. Tatsächlich verbleiben ja nur insgesamt 3 falsch kategorisierte Pinguine (1 links und 2 rechts).
- Nach der zweiten Split-Ebene wird dann direkt eine perfekte Klassifikation erreicht, sodass die Genauigkeit 100% beträgt.
- Für den zweiten Split wird links die Schnabellänge, rechts die Schnabeltiefe verwendet.
- Die anderen Features (Körpergewicht, Geschlecht) werden nicht verwendet, da sie bei der Evaluation weniger Informationsgewinn geboten haben.
- Obwohl wir
max_depth=3erlaubt haben, hört der Baum nach nur 2 Splits auf. Das passiert, weil der Algorithmus bereits nach dem zweiten Split perfekte Klassifikation (100% Genauigkeit) erreicht hat. Alle Blattknoten sind dann “rein” (enthalten nur eine Klasse), sodass weitere Splits keinen Informationsgewinn mehr bringen würden3.
Feature Importance: Welche Features sind wichtig?
Ein weiteres Konzept bei Decision Trees ist die Feature Importance (Feature-Wichtigkeit). Sie misst, wie viel jedes Feature zur Verbesserung der Reinheit des gesamten Baums beiträgt.
Berechnung der Feature Importance
Für jedes Feature wird die Importance folgendermaßen berechnet:
\[\text{Importance}(f) = \sum_{t \in \text{Splits mit } f} \frac{n_t}{n} \cdot \text{Information Gain}_t\]
wobei:
- \(f\) das Feature ist
- \(t\) alle Splits (Knoten) sind, die dieses Feature verwenden
- \(n_t\) die Anzahl Samples im Knoten \(t\)
- \(n\) die Gesamtanzahl Samples
- \(\text{Information Gain}_t\) der Informationsgewinn des Splits
Einfach ausgedrückt: Die Importance ist die gewichtete Summe aller Informationsgewinne, die durch dieses Feature erzielt wurden. Features, die früh im Baum verwendet werden und große Samples-Mengen trennen, erhalten dementsprechend höhere Importance-Werte.
# Feature Importance anzeigen
feature_names = ['Körpergewicht', 'Geschlecht', 'Flügellänge', 'Schnabellänge', 'Schnabeltiefe']
print("Feature Importance:")
for name, importance in zip(feature_names, tree_all.feature_importances_):
print(f"{name}: {importance:.3f}")
# Visualisierung der Feature Importance
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
importance_values = tree_all.feature_importances_
sorted_idx = np.argsort(importance_values)[::-1]
ax.bar(range(len(feature_names)), importance_values[sorted_idx])
ax.set_xticks(range(len(feature_names)))
ax.set_xticklabels([feature_names[i] for i in sorted_idx], rotation=45)
ax.set_ylabel('Feature Importance')
ax.set_title('Wichtigkeit der Features im Decision Tree')
plt.show()Feature Importance:
Körpergewicht: 0.000
Geschlecht: 0.000
Flügellänge: 0.955
Schnabellänge: 0.015
Schnabeltiefe: 0.030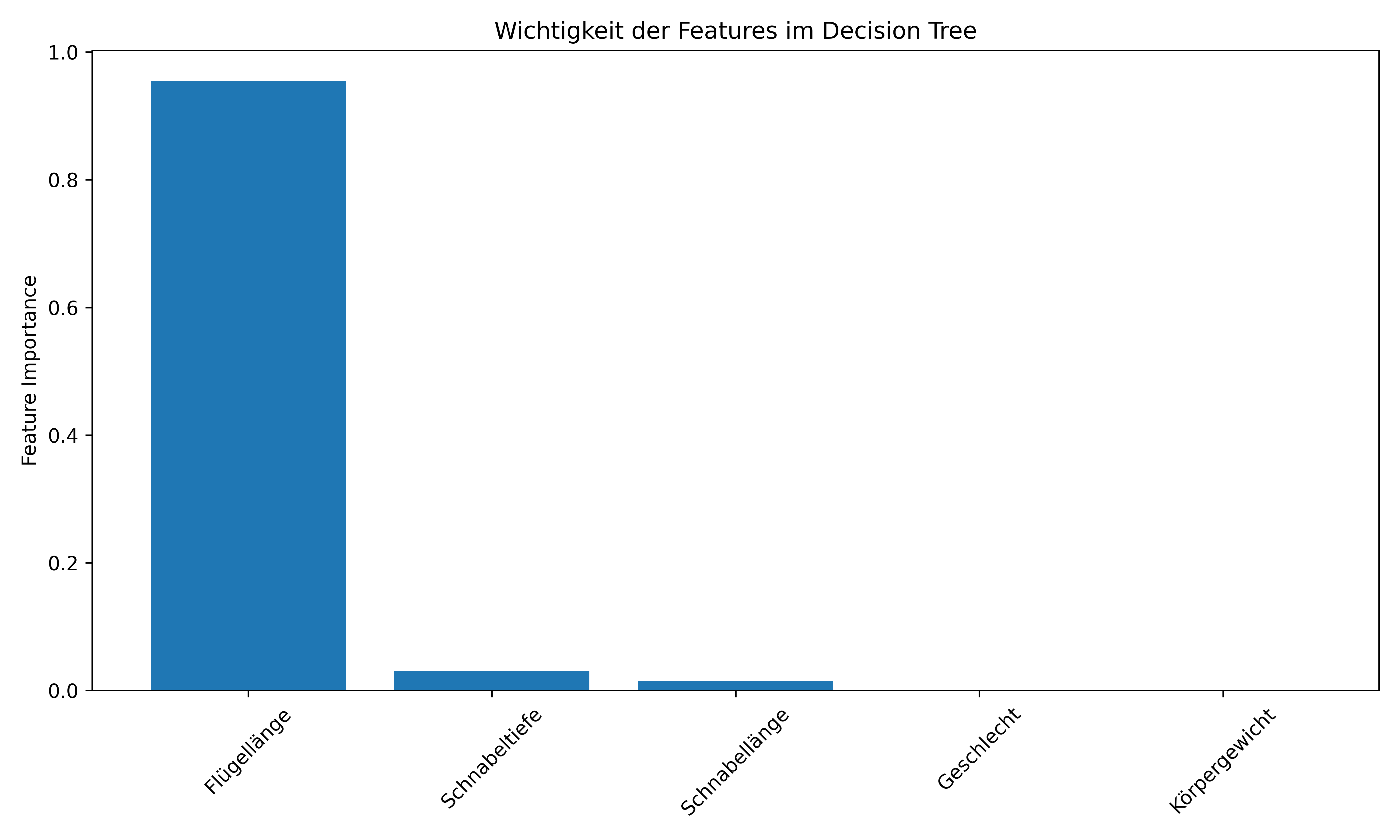
Die Feature Importance Werte summieren sich immer zu 1.0 auf. Ein Wert von 0.0 bedeutet, dass das Feature gar nicht verwendet wurde, während höhere Werte eine größere Rolle bei der Klassifikation anzeigen.
Wie zu erwarten hat Flügellänge hier mit Abstand die höchste Importance, da sie den ersten Split und sehr effektiven Split liefert. Schnabellänge und Schnabeltiefe gehen beide in die zweite Split-Ebene ein, aber da Schnabellänge nur hilft den einen falsch-kategorisierten Pinguin links zu klassifizieren, ist ihre Importance auch nur halb so groß wie die der Schnabeltiefe, die die zwei falsch-kategorisierten Pinguine rechts klassifiziert.
Das zeigt die Stärke von Decision Trees: Der Algorithmus findet automatisch die optimale Kombination von Features und deren Schwellenwerten und zeigt uns transparent, welche Features am wichtigsten sind.
Kommunikative Stärke: Erklärbarkeit für alle
Ein entscheidender Vorteil von Decision Trees liegt in ihrer außergewöhnlichen Erklärbarkeit. Während andere ML-Methoden oft als “Black Box” wahrgenommen werden, können Decision Trees von jedem verstanden werden:
- REGEL 1: Wenn Flügellänge ≤ 206.5mm → Adelie
- REGEL 2: Wenn Flügellänge > 206.5mm UND Schnabeltiefe ≤ 14.35mm → Gentoo
- REGEL 3: Wenn Flügellänge > 206.5mm UND Schnabeltiefe > 14.35mm → Adelie
Im Geschäftskontext kann diese Transparenz sehr viel Wert sein:
- Compliance: Regulierte Industrien benötigen nachvollziehbare Entscheidungen
- Debugging: Fehlerhafte Vorhersagen können direkt zurückverfolgt werden
- Stakeholder Buy-in: Führungskräfte vertrauen verständlichen Modellen eher
- Domain Knowledge: Experten können die gelernten Regeln validieren und verfeinern
Vor- und Nachteile
Vorteile von Decision Trees
Außergewöhnlich interpretierbar: Jeder Pfad im Baum ist eine verständliche Wenn-Dann-Regel. Ihr könnt jeden Entscheidungsschritt für jede Vorhersage exakt nachvollziehen und sogar Nicht-Technikern erklären.
Automatische Feature-Auswahl: Der Algorithmus ignoriert irrelevante Features automatisch und findet die wichtigsten Variablen. Feature Importance zeigt transparent, welche Variablen tatsächlich zur Vorhersage beitragen.
Minimale Datenvorverarbeitung: Decision Trees sind robust gegenüber: - Unterschiedlichen Skalen (Normalisierung nicht nötig) - Fehlenden Werten (durch Surrogate-Splits) - Gemischten Datentypen (kategorisch + numerisch) - Ausreißern (durch rekursive Partitionierung)
Schnell und effizient: Training und Vorhersage sind sehr effizient, auch bei großen Datensätzen. Der greedy Algorithmus findet schnell gute (wenn auch nicht unbedingt optimale) Lösungen.
Vielseitig einsetzbar: Sowohl für Klassifikation als auch Regression verwendbar (siehe unten), können multimodale Probleme und komplexe Interaktionen zwischen Features natürlich modellieren.
Keine parametrischen Annahmen: Decision Trees machen keine Annahmen über die Verteilung der Daten oder die funktionale Form der Zusammenhänge.
Nachteile
Instabilität: Kleine Änderungen in den Daten können zu völlig unterschiedlichen Bäumen führen. Diese hohe Varianz macht einzelne Decision Trees oft unzuverlässig.
Starke Overfitting-Neigung: Ohne Kontrolle können Decision Trees sehr spezifische, schwer generalisierbare Regeln lernen.
Schwäche bei glatten Zusammenhängen: Decision Trees approximieren glatte Kurven durch Treppen-Funktionen, was ineffizient sein kann. Lineare Zusammenhänge werden durch viele kleine Splits schlecht dargestellt (mehr dazu z.B. hier)
Bias zu dominanten Klassen: Bei unbalancierten Datensätzen neigen Decision Trees dazu, die häufigste Klasse zu bevorzugen.
Overfitting kontrollieren und optimale Komplexität finden
Das Hauptproblem von Decision Trees ist ihre Neigung zum Overfitting. Ein unrestringierter Baum würde so lange wachsen, bis jeder Datenpunkt perfekt klassifiziert ist - was zu einem Modell führt, das die Trainingsdaten “auswendig lernt” statt zu generalisieren.
Es gilt also wie so oft eine Balance zu finden zwischen Underfitting (zu flachen Bäumen) und Overfitting (zu tiefen Bäumen). Im Grunde hatten wir eine Art dieses Problems bereits in Schritt 3: Dort hatte der erste Split nach Flüggellänge schon nahezu perfekte Klassifikation erreicht, aber es wurden noch zwei weitere Splits durchgeführt um 3 (von 265!) Pinguinen auch noch korrekt zu klassifizieren.
Man kann sich demnach auch Fälle vorstellen, bei dem ein Decision Tree beispielsweise nach 5 Splits bereits 90% korrekt klassifiziert, aber dann noch 10 weitere Splits macht um die restlichen 10% zu klassifizieren. Das wäre Overfitting, da das Modell dann höchstwahrscheinlich zu spezifisch auf die Trainingsdaten angepasst ist und bei neuen Daten schlechter abschneiden würde.
Wichtigste Hyperparameter zur Komplexitätskontrolle
Decision Trees bieten verschiedene Hyperparameter zur Overfitting-Kontrolle:
max_depth: Maximale Tiefe des Baums. Begrenzt die Anzahl der Splits und verhindert so zu komplexe Bäume. Ein flacherer Baum ist weniger anfällig für Overfitting.
min_samples_split: Mindestanzahl an Datenpunkten, die ein Knoten haben muss, um gesplittet zu werden. Höhere Werte führen zu konservativeren Splits und kleineren Bäumen.
min_samples_leaf: Mindestanzahl an Datenpunkten, die in einem Blattknoten verbleiben müssen. Verhindert, dass der Baum zu spezifische Regeln für einzelne Datenpunkte lernt.
min_impurity_decrease: Minimaler Informationsgewinn, der für einen Split erforderlich ist. Splits, die nur geringfügige Verbesserungen bringen, werden nicht durchgeführt.
Die Wahl der Hyperparameter ist oft eine Kombination aus:
- Domain-Wissen: Wie komplex ist das Problem? Wieviele Regeln sind realistisch?
- Datensatzgröße: Kleinere Datensätze benötigen konservativere Einstellungen
- Interpretierbarkeit: Flachere Bäume sind leichter zu verstehen
- Experimentation: Verschiedene Werte ausprobieren und die Performance beobachten
Gerade letzteres lässt sich wiederum systematisch automatisieren, z.B. mittels GridSearchCV oder RandomizedSearchCV. Diese Methoden testen verschiedene Kombinationen von Hyperparametern und wählen die beste basierend auf Cross-Validation-Performance. Das betrachten wir aber in einem späteren Kapitel.
Komplettes Beispiel
Hier ist der komplette Workflow für einen Decision Tree - von der Datenaufbereitung bis zur finalen Evaluation:
# Notwendige Module importieren
import pandas as pd
import numpy as np
from sklearn.model_selection import RepeatedStratifiedKFold, cross_validate
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Daten für binäre Klassifikation vorbereiten
penguins_binary = (
penguins
.loc[penguins['species'].isin(['Gentoo', 'Adelie']), ['species', 'body_mass_g', 'sex', 'flipper_length_mm', 'bill_length_mm', 'bill_depth_mm']] # Nur Gentoo und Adelie auswählen
.dropna() # Fehlwerte entfernen
)
# Binäre Zielvariable erstellen (1 = Gentoo, 0 = Adelie)
penguins_binary['species_binary'] = (penguins_binary['species'] == 'Gentoo').astype(int)
# Kategorische Variable encodieren (1 = male, 0 = female)
penguins_binary['sex_encoded'] = penguins_binary['sex'].map({'male': 1, 'female': 0})
# Decision Tree mit Repeated Stratified Cross Validation
model = DecisionTreeClassifier(max_depth=3, random_state=42); # Decision Tree Modell initialisieren
X = penguins_binary[['body_mass_g', 'sex_encoded', 'flipper_length_mm', 'bill_length_mm', 'bill_depth_mm']] # Unabhängige Variablen: Penguin-Features
y = penguins_binary['species_binary'] # Abhängige Variable: Art (binär kodiert)
# Repeated Stratified K-Fold für balancierte Test-Sets verwenden
cv = RepeatedStratifiedKFold(n_splits=5, n_repeats=10, random_state=42);
# Cross Validation mit mehreren Metriken durchführen
cv_tree_results = cross_validate(
model, X, y, # Modell und Daten
cv=cv, # Stratified K-Fold Validierung
scoring=['accuracy', 'precision', 'recall', 'f1', 'roc_auc'], # Klassifikationsmetriken
return_train_score=True # Auch Training-Scores berechnen
);
# Ergebnisse in DataFrame organisieren
results_data = []
for metric in ['accuracy', 'precision', 'recall', 'f1', 'roc_auc']:
test_scores = cv_tree_results[f'test_{metric}'] # Test-Scores für aktuelle Metrik
results_data.append({
'Metrik': metric.upper(),
'Durchschnitt': test_scores.mean(),
'StdAbw': test_scores.std(),
'Min': test_scores.min(),
'Max': test_scores.max()
})
# DataFrame erstellen und anzeigen
results_df = pd.DataFrame(results_data)
print("Decision Tree - Repeated Stratified Cross Validation:")
print(results_df.round(3))
# Feature Importance anzeigen (Modell einmal auf allen Daten trainieren)
model.fit(X, y);
feature_names = ['Körpergewicht', 'Geschlecht', 'Flügellänge', 'Schnabellänge', 'Schnabeltiefe']
print("\nFeature Importance:")
for name, importance in zip(feature_names, model.feature_importances_):
print(f"{name}: {importance:.3f}")
# Visualisierung des finalen Baums
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
plot_tree(model,
feature_names=feature_names,
class_names=['Adelie', 'Gentoo'],
filled=True,
rounded=True,
fontsize=10,
ax=ax)
ax.set_title('Decision Tree für Pinguin-Klassifikation')
plt.show()Decision Tree - Repeated Stratified Cross Validation:
Metrik Durchschnitt StdAbw Min Max
0 ACCURACY 0.991 0.016 0.943 1.0
1 PRECISION 0.990 0.019 0.920 1.0
2 RECALL 0.989 0.020 0.917 1.0
3 F1 0.990 0.017 0.936 1.0
4 ROC_AUC 0.990 0.016 0.941 1.0
Feature Importance:
Körpergewicht: 0.000
Geschlecht: 0.000
Flügellänge: 0.955
Schnabellänge: 0.015
Schnabeltiefe: 0.030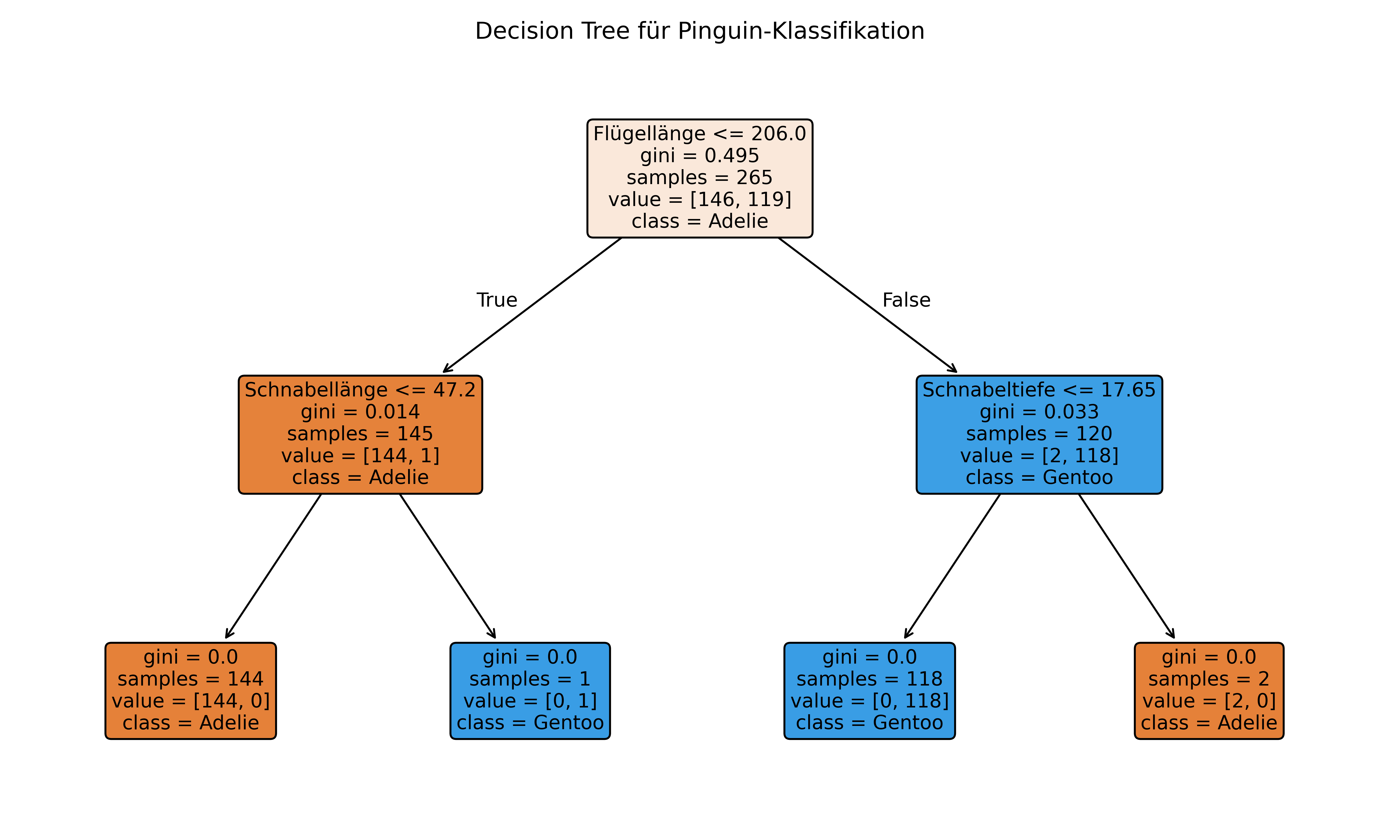
Dieser Code zeigt den kompletten Workflow: In nur wenigen Zeilen können wir einen Decision Tree trainieren und evaluieren. Das ist die Stärke von scikit-learn - komplexe Machine Learning Algorithmen werden durch einfache, einheitliche APIs zugänglich gemacht.
Extra: eigener Farbgradient
Die Standard-Visualisierung von sklearn’s plot_tree() verwendet immer die gleichen Farben: Orange und Blau für binäre Klassifikation. Es gibt erstaunlicherweise keinen direkten Parameter, um diese Farben zu ändern - ein häufiger Kritikpunkt an der Funktion.
Für thematisch passende Visualisierungen (wie Pinguinarten mit ihren charakteristischen Farben) oder zur Einhaltung von Corporate Design Guidelines ist dies aber oft erwünscht. Glücklicherweise können wir die Farben nachträglich über die matplotlib-Objekte ändern. Da das aber nicht ganz trivial ist, hier der Versuch alles in eine einfach handhabbare Funktion apply_gradient_colors() zu packen…
def apply_gradient_colors(model, artists, color_0, color_1):
"""
Färbt einen bereits erstellten Decision Tree mit Gradient-Farben ein
Parameters:
-----------
model : DecisionTreeClassifier
Das trainierte Modell
artists : list
Die von plot_tree() zurückgegebenen artists
color_0 : str
Hex-Farbe für Klasse 0
color_1 : str
Hex-Farbe für Klasse 1
"""
def mix_colors(color1_hex, color2_hex, ratio):
color1_rgb = [int(color1_hex[i:i+2], 16) for i in (1, 3, 5)]
color2_rgb = [int(color2_hex[i:i+2], 16) for i in (1, 3, 5)]
mixed_rgb = [int(color1_rgb[i] * (1-ratio) + color2_rgb[i] * ratio) for i in range(3)]
return f"#{mixed_rgb[0]:02x}{mixed_rgb[1]:02x}{mixed_rgb[2]:02x}"
# Gradient-Farben für alle Knoten berechnen
node_colors = []
for i in range(model.tree_.node_count):
values = model.tree_.value[i][0]
class1_ratio = values[1] / values.sum() if values.sum() > 0 else 0
node_colors.append(mix_colors(color_0, color_1, class1_ratio))
# Alle Artists mit BBox einfärben
bbox_count = 0
for artist in artists:
bbox = artist.get_bbox_patch()
if bbox and bbox_count < len(node_colors):
bbox.set_facecolor(node_colors[bbox_count])
bbox_count += 1… und diese Funktion dann anzuwenden:
# Unser Pinguin-Decision Tree mit thematisch passenden Farben
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
artists = plot_tree(model,
feature_names=feature_names,
class_names=['Adelie', 'Gentoo'],
filled=True,
rounded=True,
fontsize=10,
ax=ax)
# Pinguinfarben anwenden
apply_gradient_colors(model, artists, color_0='#FF8C00', color_1='#159090')
ax.set_title('Decision Tree mit Pinguin-Farbschema')
plt.show()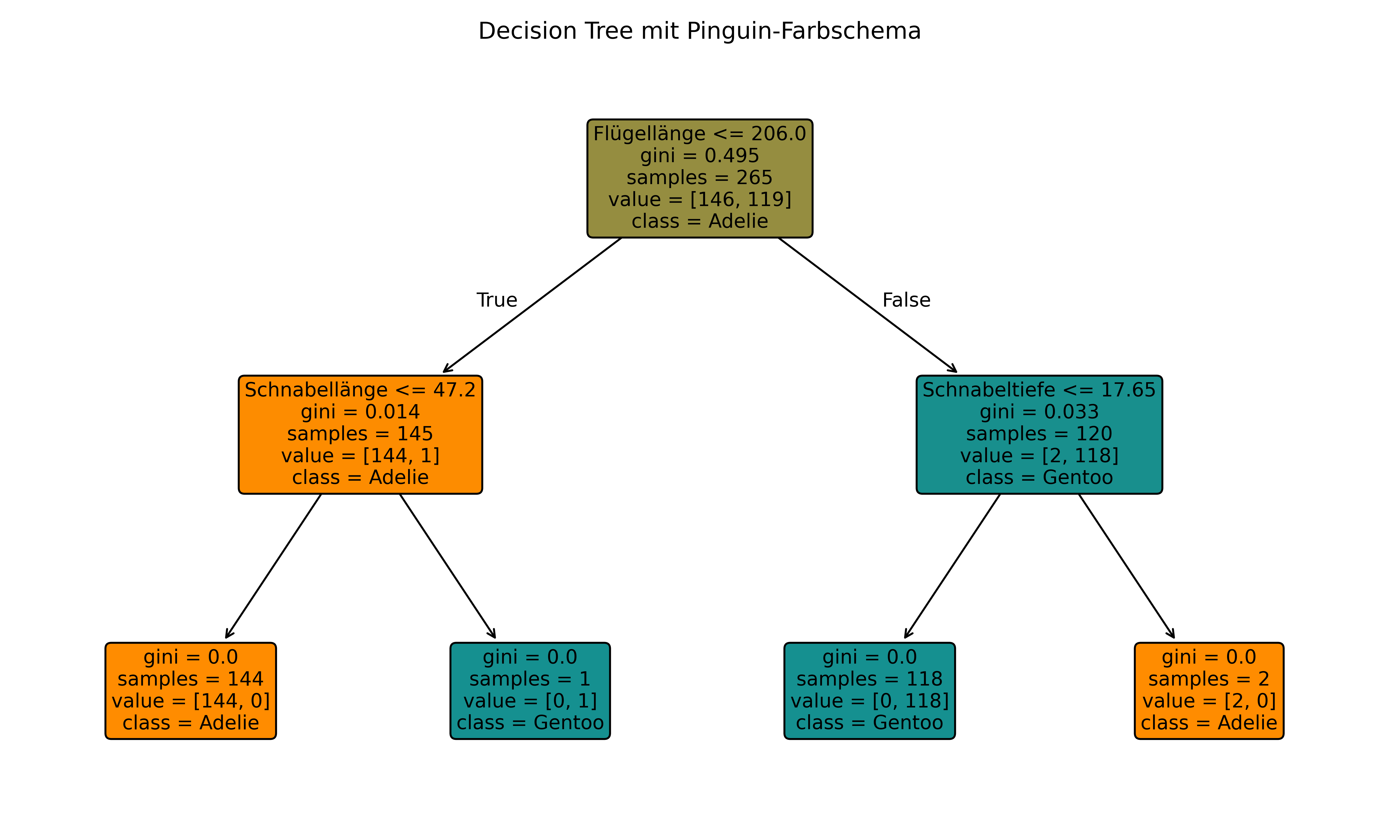
Jetzt verwendet der Baum die charakteristischen Farben der Pinguinarten:
-
Orange (
#FF8C00) für Adelie-dominierte Knoten -
Teal (
#159090) für Gentoo-dominierte Knoten
- Farbmischungen für gemischte Knoten basierend auf der exakten Klassenverteilung
Diese Funktion ist universell einsetzbar: Einfach color_0 und color_1 an eure gewünschten Farben anpassen!
Wir beschäftigen uns aktuell mit Decision Trees für Klassifikation, aber sie sind auch nützlich für Regressionsprobleme, also zur Vorhersage von kontinuierlichen Werten. Dies geschieht, indem sie die Daten in homogene Gruppen aufteilen und den Mittelwert der Zielvariable in jedem Blattknoten verwenden. Der grundlegende Algorithmus ist derselbe, aber statt Gini-Impurity oder Entropy verwendet man Mean Squared Error (MSE) als Splitting-Kriterium. Der folgende Baum zeigt ein Beispiel für einen Regression Tree, der die Flügellänge von Pinguinen vorhersagt und dabei nur die Features Körpergewicht und Schnabellänge zur Verfügung hat. Es gilt vor allen Dingen zu realisieren, dass value= jetzt hier den Mittelwert der Zielvariable in jedem Knoten anzeigt, statt die Verteilung der Klassen wie bei der Klassifikation. Zudem sind eben diese Mittelwerte auch innerhalb einer Split-Ebene immer von links nach rechts sortiert.
# Beispiel: Körpergewicht vorhersagen basierend auf anderen Features
from sklearn.tree import DecisionTreeRegressor
# Regression: flipper_length_mm vorhersagen
X_reg = penguins_clean[['body_mass_g', 'bill_length_mm']]
y_reg = penguins_clean['flipper_length_mm']
# Decision Tree für Regression
tree_reg = DecisionTreeRegressor(max_depth=3, random_state=42)
tree_reg.fit(X_reg, y_reg);
# Visualisierung
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
plot_tree(tree_reg,
feature_names=['Körpergewicht', 'Schnabellänge'],
filled=True,
rounded=True,
fontsize=8,
ax=ax)
ax.set_title('Decision Tree Regression: Flügellänge vorhersagen')
plt.show()
print(f"R² Score: {tree_reg.score(X_reg, y_reg):.3f}")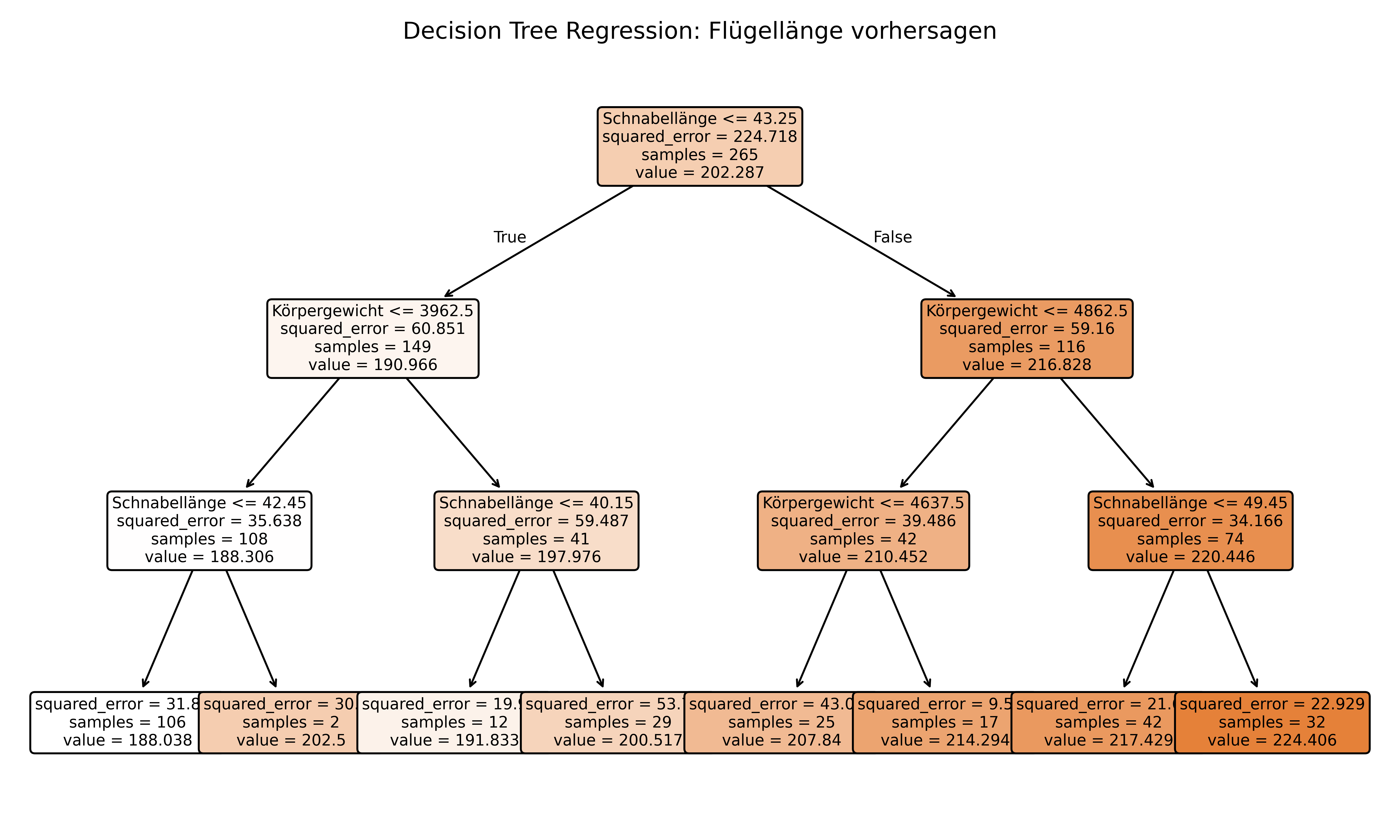
R² Score: 0.864Unterschiede zur Klassifikation:
- Splitting-Kriterium: MSE statt Gini-Impurity
- Vorhersage: Mittelwert der Blattknoten statt Mehrheitsklasse
- Ausgabe: Kontinuierliche Werte statt Kategorien
Regression Trees sind besonders nützlich, wenn man nicht-lineare Zusammenhänge modellieren möchte, ohne spezifische funktionale Formen anzunehmen.
Übungen
In dieser Übung wendest du Decision Trees auf einen bekannten Mushroom-Datensatz an. Dieser enthält 8124 Beobachtungen von verschiedenen Pilzarten mit insgesamt 22 morphologischen und umweltbezogenen Merkmalen wie Hutform, Kiemenfarbe oder Geruch. Jeder Pilz ist als essbar (‘e’) oder giftig (‘p’) klassifiziert - ein perfektes Beispiel für ein sicherheitskritisches Klassifikationsproblem. Detaillierte Informationen zu allen Attributen findest du z.B. hier.
Datenvorverarbeitung (vorgegeben):
import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import RepeatedStratifiedKFold, cross_validate
import matplotlib.pyplot as plt
np.random.seed(42)
# Daten laden
url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/mushrooms/mushrooms.csv'
mushrooms = pd.read_csv(url)
mushrooms = mushrooms.drop(columns=['ring_number', 'veil_type', 'stalk_root'])
# Zielvariable separieren
X = mushrooms.drop('Mushroom_quality', axis=1)
y = mushrooms['Mushroom_quality']
# Encoding
y = (y == 'p').astype(int) # 0=edible, 1=poisonous
print(f"Vor One-Hot-Encoding: {X.shape[1]} Features")
X = pd.get_dummies(X, drop_first=True)
print(f"Nach One-Hot-Encoding: {X.shape[1]} Features")Hinweis zum vorgegebenen Code - Umgang mit nominalen Variablen: Da alle Features in diesem Datensatz nominale kategorische Variablen sind (z.B. hat Hutfarbe die Ausprägungen braun, gelb, weiß etc. ohne natürliche Reihenfolge), verwenden wir One-Hot-Encoding/Dummy-Kodierung via pd.get_dummies(). Dies bedeutet, dass aus einem Feature wie “cap_color” mit 10 möglichen Werten 9 binäre Features werden (z.B. “cap_color_brown”, “cap_color_yellow” etc.), wie wir es bereits im ANOVA-Kapitel bei der Dummy-Kodierung kennengelernt haben.
Übung 1: Decision Tree mit max_depth=2
Prüfe wie gut ein Decision Tree mit mxaimaler Tiefe 2 die Giftigkeit von Pilzen vorhersagen kann:
- Erstelle einen Decision Tree Klassifikator mit maximaler Tiefe 2 und einem Random State für Reproduzierbarkeit
- Verwende stratifizierte K-Fold Kreuzvalidierung mit 5 Folds und 5 Wiederholungen
- Führe Kreuzvalidierung mit mehreren Klassifikationsmaßen durch
- Erstelle eine übersichtliche Ergebnis-Tabelle mit Test- und Train-Scores. Die Tabelle soll folgende Spalten haben: Metrik; Test; Train. In der ersten Spalte steht die Bezeichnung des Klassifikationsmaßes und die anderen beiden Spalten enthalten die über die Folds aggregierten Wert im Format
"mean (±std)" - Visualisiere den Baum
Übung 2: Wichtigstes Bewertungsmaß identifizieren
Überlege, welches Klassifikationsmaß in diesem speziellen Anwendungsfall am wichtigsten ist.
Übung 3: Einfluss des wichtigsten Features
Untersuche, was passiert, wenn das wichtigste Feature weggelassen wird bevor du den Decision Tree trainierst.
- Identifiziere das wichtigste Feature aus Übung 1 mittels Feature Importance
- Trainiere einen neuen Decision Tree (max_depth=2) OHNE das wichtigste Feature
- Führe Kreuzvalidierung durch und vergleiche die Performance mit dem ursprünglichen Modell
- Visualisiere auch diesen neuen Baum
- Was ändert sich? Welches Feature wird nun am wichtigsten?
Übung 4: Tieferer Baum
Nimm wieder alle Features rein und trainiere einen Decision Tree mit max_depth=10 und untersuche die Auswirkungen eines tieferen Baums.
- Erstelle einen Decision Tree Klassifikator mit maximaler Tiefe 10
- Führe Kreuzvalidierung durch und vergleiche mit dem flacheren Baum (max_depth=2)
- Visualisiere den tiefen Baum
- Vergleiche die Komplexität: Anzahl Blätter und tatsächliche Tiefe
Fußnoten
Das bedeutet für numerische Features nicht jede mögliche Zahl (das wären ja unendlich viele), sondern all die, die überhaupt auch zwei Werte im Datensatz voneinander trennen würden. Sklearn nimmt dafür immer die Mitte(lwerte) zwischen zwei aufeinanderfolgenden Werte. Also sprich, bei einem Datensatz
1, 2, 4würde der Algorithmus die Splits1.5und3testen.↩︎Random State sorgt dafür, dass der Algorithmus bei jedem Lauf die gleiche Entscheidung trifft. Falls ihr euch fragt was bei diesem Prozess überhaupt dem Zufall überlassen ist: Wenn zwei oder mehr Features den exakt gleichen Information Gain liefern, wird zufällig einer davon ausgewählt. Außerdem könnte euer Datensatz auch so viele Features haben, dass der Algorithmus nicht alle möglichen Splits testen kann, weil es zu lange dauern würde. Das wird dann durch
max_featureskontrolliert und diese Teilmenge aller Features wird zufällig ausgewählt.↩︎Das erklärt auch warum in Schritt 2 der Baum mit
max_depth=2und nur einem Feature (Körpergewicht) trotz ausbleibender Verbesserung noch einen zweiten Split gemacht hat: Der Algorithmus hat ja noch nicht perfekte Klassifikation erreicht, sodass er weiter Splits machen kann. Erst wenn er 100% Genauigkeit erreicht, hört er von alleine auf.↩︎