import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.metrics import silhouette_score
from scipy.cluster.hierarchy import dendrogram, linkage, fcluster
from sklearn.cluster import DBSCAN
import seaborn as sns
np.random.seed(42)K-means Clustering
Nachdem wir mit der Principal Component Analysis unsere erste Methode des unüberwachten Lernens kennengelernt haben, wenden wir uns nun dem Clustering zu. Clustering ist eine weitere wichtige Kategorie des unüberwachten Lernens, bei der das Ziel darin besteht, natürliche Gruppen in den Daten zu entdecken, ohne vorher zu wissen, welche Gruppen existieren. Da wir bereits sehr viele Kapitel mit dem Klassifizieren verbracht haben, betone ich das hier nochmal extra: Wir versuchen primär nicht bereits bekannte Klassen wiederzufinden, sondern wir gehen mal wirklich davon aus, dass wir keinerlei Wissen über womöglich bekannte Klassen haben und schauen aber nach ob ein Clustering in verschiedene Klassen hier möglich/sinnvoll ist. Wir entdecken Ähnlichkeitsstrukturen in (meist relativ großen) Datenbeständen. Die so gefundenen Gruppen von „ähnlichen” Objekten werden als Cluster bezeichnet, die Gruppenzuordnung als Clustering.
Es gibt verschieden Algorithmen mit denen man clustern kann. K-means Clustering ist einer der ältesten und populärsten Clustering-Algorithmen. Die Grundidee ist die Daten in \(k\) Gruppen (Cluster) aufzuteilen, sodass Datenpunkte innerhalb eines Clusters möglichst ähnlich sind, während Datenpunkte verschiedener Cluster möglichst unähnlich sind. Ob Datenpunkte sich ähnlich sind, wird von der Distanz zwischen Ihnen abgeleitet.
Somit haben k-means Clustering und k-nearest-neighbors direkt zwei Dinge gemeinsam: Sie basieren auf Distanzberechnungen und man muss ein \(k\) vorgeben.
Datengrundlage: Unüberwachtes Vorgehen
Für unser Clustering-Beispiel nehmen wir dementsprechend eine bewusst unüberwachte Herangehensweise: Stellen wir uns vor, wir hätten Messdaten von 342 Pinguinen bekommen - mit Schnabellänge, Schnabeltiefe, Flossenlänge und Körpergewicht - aber ohne jegliche Information über Pinguinarten. Wir wissen nicht einmal genau, wie viele verschiedene Arten es gibt!
Unser Ziel ist es herauszufinden, ob sich in diesen Messdaten natürliche Gruppen entdecken lassen. Wir behalten die species Spalte aber dennoch bei - auch wenn wir so tun als hätten wir die Information nicht.
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Farben für die echten Pinguinarten (nur für Vergleiche)
species_colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
# Daten vorbereiten - alle numerischen Features verwenden
numeric_features = ['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']
penguins_clean = penguins.dropna(subset=numeric_features + ['species'])
print(f"Datensatz: {len(penguins_clean)} Pinguine mit {len(numeric_features)} Features")
print(f"Features: {numeric_features}")
# Feature Matrix erstellen (ohne Species-Information zu verwenden!)
X = penguins_clean[numeric_features].values
y_species = penguins_clean['species'].values # Behalten wir nur für spätere VergleicheDatensatz: 342 Pinguine mit 4 Features
Features: ['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'body_mass_g']Da k-means auf Distanzberechnungen basiert (genau wie k-Nearest Neighbors), müssen wir die Features standardisieren, damit alle fair zur Cluster-Bildung beitragen können. Alle Features haben dann wie gehabt Mittelwert ≈ 0 und Standardabweichung = 1. Wir wenden die Standardisierung hier auf die gesamten Daten an, da wir zu keiner Zeit in diesem Kapitel einen Train-Test-Split durchführen werden, sodass es auch kein Data Leakage geben kann.
# Feature Scaling durchführen
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)K-means Algorithmus: Die Grundidee
Der k-means Algorithmus verfolgt eine iterative Strategie mit einem Initialisierungsschritt und zwei sich wiederholenden Hauptschritten. Die Hauptschritte wiederholen sich so lange, bis eine Konvergenz oder die vorgegebene, maximal erlaubte Anzahl an Iterationen erreicht wurde:
Schritt 0: Initialisierung
- Setze zufällig \(k\) Zentroide (Cluster-Zentren) in den Datenraum
- Diese initialen Positionen bestimmen den Startpunkt des Algorithmus
Schritt 1: Zuordnung (Assignment)
- Weise jeden Datenpunkt dem nächstgelegenen Zentroid zu
- Jeder Punkt erhält das Label des Clusters, zu dem er nun gehört
Schritt 2: Aktualisierung (Update)
- Berechne neue Zentroide als Mittelwert aller Punkte die in Schritt 1 dem jeweiligen Cluster zugeordnet wurden
- Die Zentroide “wandern” nun zu den neuen Schwerpunkten ihrer zugeordneten Punkte
Ergebnis
- Falls Schritt 2 zu keiner Veränderung des Zentroids geführt hat, also die neue Position dieselbe ist wie die alte, so sprechen wir von einer Konvergenz und der Algorithmus ist fertig.
- Alternativ kann es auch sein, dass wir eine maximale Anzahl an erlaubten Iterationen durch Schritte 1 und 2 erreicht haben - auch dann hört der Algorithmus auf zu iterieren.
- Wir haben also finale Zentroide und Cluster ermittelt.
Eine exzellente animierte Darstellung dieses Prozesses findest du in diesem Video: K-Means Algorithm Visualization.
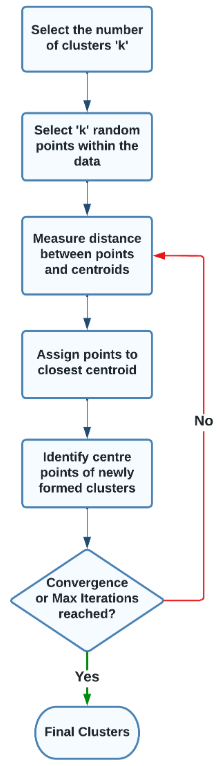
Quelle: Andy McDonald
Erstes einfaches Beispiel: Zwei Features
Bevor wir alle vier Features verwenden, schauen wir uns K-means zunächst mit nur zwei Features an: Schnabellänge und Schnabeltiefe. So können wir das Clustering perfekt visualisieren und verstehen, was der Algorithmus macht.
# Nur zwei Features für einfache Visualisierung auswählen
features_2d = ['bill_length_mm', 'bill_depth_mm']
# Entsprechende Spalten aus den bereits standardisierten Daten extrahieren
feature_indices = [numeric_features.index(feat) for feat in features_2d]
X_2d_scaled = X_scaled[:, feature_indices]Zuerst schauen wir uns die Daten ohne jegliche Gruppierung an und dann führen wir K-means mit \(k=3\) durch. Dazu verwenden wir KMeans aus dem sklearn.cluster Modul. Die wichtigsten Parameter sind:
-
n_clusters=3: Dies ist \(k\) - Wir möchten 3 Cluster finden -
random_state=42: Sorgt für reproduzierbare Ergebnisse bei der zufälligen Initialisierung -
n_init=10: Der Algorithmus wird 10-mal mit verschiedenen Startpunkten ausgeführt und das beste Ergebnis gewählt (später mehr dazu)
# K-means mit k=3 durchführen
kmeans_2d = KMeans(n_clusters=3, random_state=42, n_init=10)
cluster_labels_2d = kmeans_2d.fit_predict(X_2d_scaled)Code zeigen/verstecken
# Visualisierung: Rohdaten vs. K-means Clustering
fig, axes = plt.subplots(1, 2, figsize=(14, 6), layout='tight')
# Links: Rohdaten (alle Punkte schwarz)
ax = axes[0]
ax.scatter(X_2d_scaled[:, 0], X_2d_scaled[:, 1],
c='black', alpha=0.7, s=50)
ax.set_xlabel(f'{features_2d[0]} (standardisiert)')
ax.set_ylabel(f'{features_2d[1]} (standardisiert)')
ax.set_title('Rohdaten ohne Clustering')
ax.grid(True, alpha=0.3)
# Rechts: K-means Cluster
ax = axes[1]
cluster_colors_2d = ['#e41a1c', '#377eb8', '#4daf4a'] # Rot, Blau, Grün
for i, color in enumerate(cluster_colors_2d):
mask = cluster_labels_2d == i
ax.scatter(X_2d_scaled[mask, 0], X_2d_scaled[mask, 1],
c=color, label=f'Cluster {i}', alpha=0.7, s=50)
# Zentroide als X-Symbole hervorheben
ax.scatter(kmeans_2d.cluster_centers_[:, 0], kmeans_2d.cluster_centers_[:, 1],
c='black', marker='X', s=200, linewidth=2, label='Zentroide', edgecolor='white')
ax.set_xlabel(f'{features_2d[0]} (standardisiert)')
ax.set_ylabel(f'{features_2d[1]} (standardisiert)')
ax.set_title('K-means Clustering (k=3)')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
Die schwarzen X-Symbole sind die Zentroide - die Mittelpunkte der gefundenen Cluster.
Verschiedene k-Werte ausprobieren
Natürlich wissen wir nicht vorab, dass \(k=3\) die beste Wahl ist. Schauen wir uns an, was passiert, wenn wir verschiedene Anzahlen von Clustern ausprobieren:
# Verschiedene k-Werte testen
k_values = [2, 3, 4, 5]
cluster_results = {}
for k in k_values:
kmeans_k = KMeans(n_clusters=k, random_state=42, n_init=10)
labels_k = kmeans_k.fit_predict(X_2d_scaled)
cluster_results[k] = {
'model': kmeans_k,
'labels': labels_k,
'centers': kmeans_k.cluster_centers_,
'inertia': kmeans_k.inertia_
}Code zeigen/verstecken
# 2x2 Subplot für verschiedene k-Werte
fig, axes = plt.subplots(2, 2, figsize=(14, 12), layout='tight')
axes = axes.flatten()
# Farbpalette für verschiedene k-Werte
colors_palette = ['#e41a1c', '#377eb8', '#4daf4a', '#984ea3', '#ff7f00']
for idx, k in enumerate(k_values):
ax = axes[idx]
labels = cluster_results[k]['labels']
centers = cluster_results[k]['centers']
inertia = cluster_results[k]['inertia']
# Datenpunkte nach Clustern einfärben
for i in range(k):
mask = labels == i
ax.scatter(X_2d_scaled[mask, 0], X_2d_scaled[mask, 1],
c=colors_palette[i], alpha=0.7, s=50, label=f'Cluster {i}')
# Zentroide als X-Symbole
ax.scatter(centers[:, 0], centers[:, 1],
c='black', marker='X', s=200, linewidth=2,
label='Zentroide', edgecolor='white')
ax.set_xlabel(f'{features_2d[0]} (standardisiert)')
ax.set_ylabel(f'{features_2d[1]} (standardisiert)')
ax.set_title(f'K-means mit k={k}')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
Beobachtungen:
- k=2: Teilt die Daten in zwei große Gruppen - zu grob?
- k=3: Drei natürliche Cluster - wirkt ausgewogen
- k=4: Ein Cluster wurde weiter unterteilt - sinnvoll oder Überanpassung?
- k=5: Noch feinere Unterteilung - möglicherweise zu viele Cluster
Aber wie können wir systematisch entscheiden, welches \(k\) am besten ist? Hier kommen objektive Bewertungsmethoden ins Spiel.
Inertia: Die Zielfunktion von K-means
Bevor wir zu den Entscheidungsmethoden kommen, müssen wir verstehen, was K-means eigentlich optimiert. Die Inertia (auch “Within-Cluster Sum of Squares” genannt) ist die Zielfunktion, die K-means minimiert:
\(\text{Inertia} = \sum_{i=0}^{n-1} \min_{\mu_j \in C} (||x_i - \mu_j||^2)\)
Anders ausgedrückt: Die Summe der quadrierten Abstände aller Datenpunkte zu ihren jeweiligen Cluster-Zentren. Kleinere Inertia-Werte bedeuten kompaktere, homogenere Cluster.
# Inertia-Werte für verschiedene k vergleichen
print("Inertia-Werte für verschiedene k:")
for k in k_values:
inertia = cluster_results[k]['inertia']
print(f" k={k}: {inertia:.2f}")Inertia-Werte für verschiedene k:
k=2: 340.18
k=3: 186.92
k=4: 147.81
k=5: 114.04Wichtige Erkenntnisse:
- Inertia sinkt immer mit steigendem k (mehr Cluster = kleinere Abstände)
- Bei k=n (jeder Punkt ein eigenes Cluster) wäre Inertia = 0
- Aber kleinste Inertia bedeutet nicht bestes Clustering!
- Wir suchen den optimalen Trade-off zwischen Einfachheit und Cluster-Qualität
Die Inertia können wir aus jedem trainierten KMeans-Objekt mit .inertia_ abrufen. Diese Werte sind die Grundlage für systematische k-Wahl-Methoden. Dies geschieht i.d.R. mit der Elbow-Methode oder dem Silhouette Score.
Elbow-Methode
Die Elbow-Methode basiert auf der Inertia und sucht den “Ellbogen” in der Inertia-Kurve - den Punkt, ab dem zusätzliche Cluster kaum noch Verbesserung bringen. Wir erweitern unsere k-Range auf k-Werte von 1-10, um den Trend besser zu erkennen:
# Erweiterte k-Range für Elbow-Methode
k_range_extended = range(1, 11)
inertias = []
for k in k_range_extended:
kmeans = KMeans(n_clusters=k, random_state=42, n_init=10);
kmeans.fit(X_2d_scaled);
inertias.append(kmeans.inertia_);
# Verbesserungen berechnen
improvements = [inertias[i-1] - inertias[i] for i in range(1, len(inertias))]
print("Inertia-Verbesserungen (absolut):")
for i, improvement in enumerate(improvements, 2):
print(f" k={i-1} → k={i}: {improvement:.1f}")Inertia-Verbesserungen (absolut):
k=1 → k=2: 343.8
k=2 → k=3: 153.3
k=3 → k=4: 39.1
k=4 → k=5: 33.8
k=5 → k=6: 19.7
k=6 → k=7: 11.7
k=7 → k=8: 9.2
k=8 → k=9: 8.9
k=9 → k=10: 6.5Code zeigen/verstecken
# Elbow-Plot visualisieren
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
ax.plot(k_range_extended, inertias, 'bo-', linewidth=2, markersize=8)
ax.set_xlabel('Anzahl Cluster (k)')
ax.set_ylabel('Inertia (Within-Cluster Sum of Squares)')
ax.set_title('Elbow-Methode für optimales k')
ax.grid(True, alpha=0.3)
ax.set_xticks(k_range_extended)
# Vermuteten "Elbow" bei k=3 hervorheben
ax.axvline(x=3, color='red', linestyle='--', alpha=0.7, label='Vermuteter Elbow (k=3)')
ax.legend()
plt.show()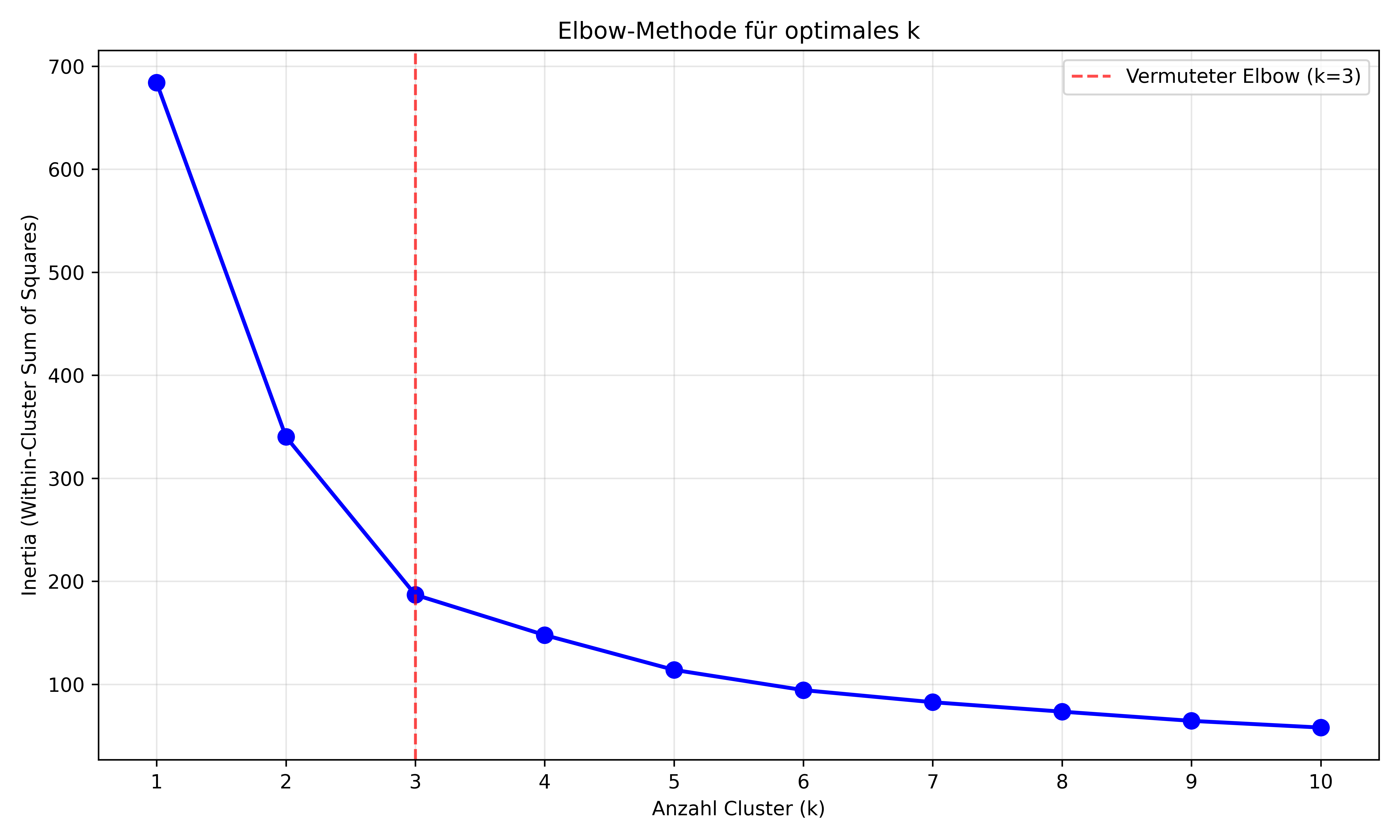
Interpretation: Der “Ellbogen” ist der Punkt, wo die Kurve beginnt, flacher zu werden. Der steile Teil vor diesem Punkt stellt also sozusagen den Oberarm dar, während alles nach dem Ellbogen den angewinkelten Unteram darstellt. Hier scheint dieser Ellbogen bei k=3 zu liegen - ab k=4 sind die Verbesserungen deutlich geringer. Tatsächlich bleibt diese Einschätzung aber subjektiv und kann in Sonderfällen alles andere als offensichtlich sein.
Silhouette-Analyse
Der Silhouette Score misst, wie gut jeder Punkt zu seinem eigenen Cluster passt im Vergleich zu anderen Clustern. Im Grunde berechnet man dabei für jeden Punkt das Verhältnis aus Distanz zum eigenen Zentroiden auf der einen Seite und mittlere Distanz zu allen anderen Zentroiden auf der anderen Seite. Schließlich können diese Werte über alle Punkte gemittelt werden. Werte nahe +1 bedeuten gut getrennte Cluster, Werte nahe 0 bedeuten überlappende Cluster.
# Silhouette-Scores für verschiedene k berechnen
silhouette_scores = []
for k in k_range_extended:
if k == 1:
silhouette_scores.append(0) # Silhouette Score nicht für k=1 definiert
else:
kmeans = KMeans(n_clusters=k, random_state=42, n_init=10)
labels = kmeans.fit_predict(X_2d_scaled)
sil_score = silhouette_score(X_2d_scaled, labels)
silhouette_scores.append(sil_score)
# Bestes k nach Silhouette
best_k_silhouette = k_range_extended[np.argmax(silhouette_scores)]
print(f"Silhouette Scores:")
for k, score in zip(k_range_extended, silhouette_scores):
if k > 1:
print(f" k={k}: {score:.3f}")
print(f"\nBestes k nach Silhouette Score: {best_k_silhouette} (Score: {max(silhouette_scores):.3f})")Silhouette Scores:
k=2: 0.476
k=3: 0.525
k=4: 0.439
k=5: 0.399
k=6: 0.415
k=7: 0.395
k=8: 0.383
k=9: 0.377
k=10: 0.385
Bestes k nach Silhouette Score: 3 (Score: 0.525)Code zeigen/verstecken
# Silhouette-Plot
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
ax.plot(k_range_extended, silhouette_scores, 'ro-', linewidth=2, markersize=8)
ax.set_xlabel('Anzahl Cluster (k)')
ax.set_ylabel('Silhouette Score')
ax.set_title('Silhouette-Analyse')
ax.grid(True, alpha=0.3)
ax.set_xticks(k_range_extended)
# Bestes k nach Silhouette hervorheben
ax.axvline(x=best_k_silhouette, color='green', linestyle='--', alpha=0.7,
label=f'Bestes k={best_k_silhouette}')
ax.legend()
plt.show()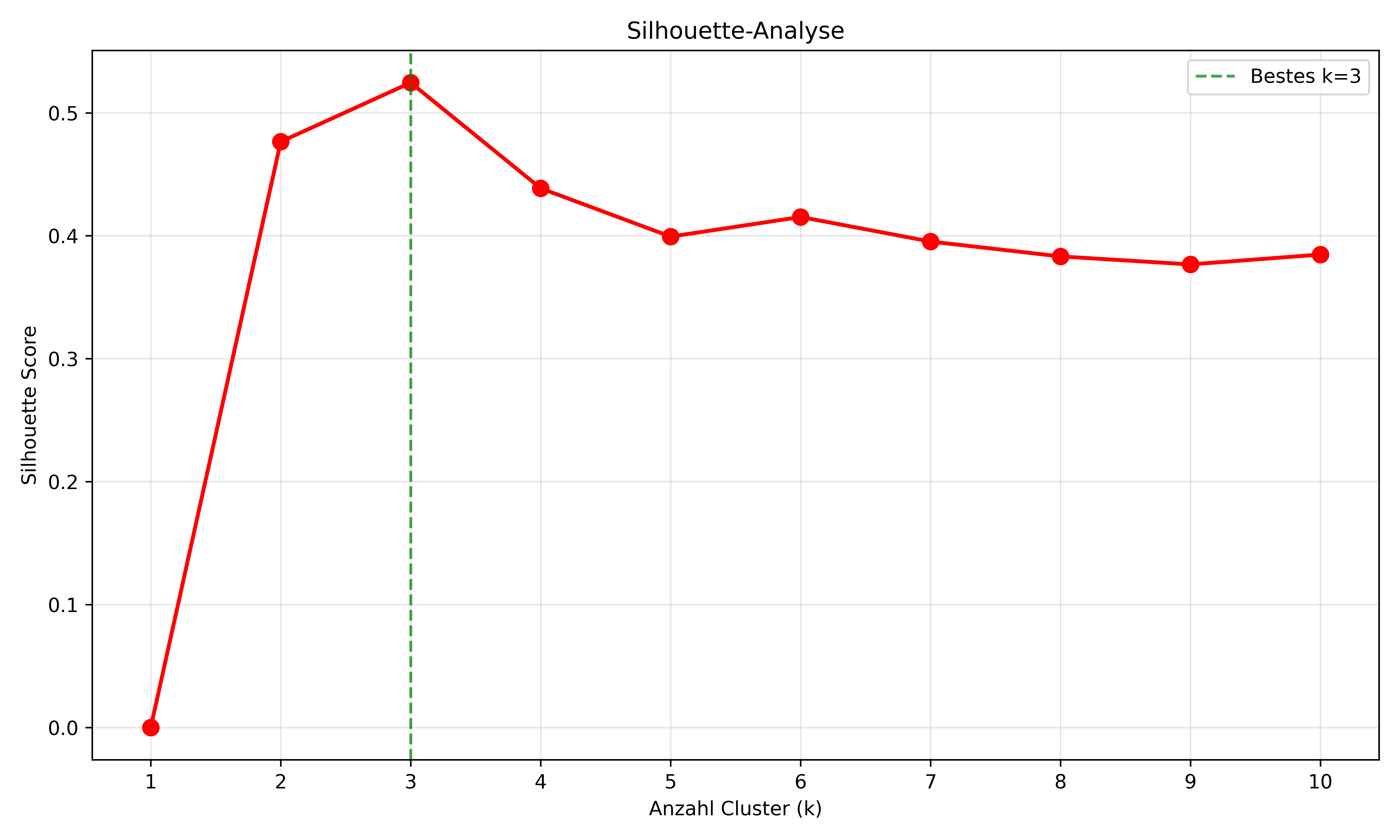
Die Silhouette-Analyse bestätigt k=3 als optimale Wahl für diese Daten.
K-means++ und Stabilität
Bis jetzt könnte der Eindruck entstanden sein, dass K-means einfach einmalig zufällige Startzentroide in den Raum wirft und dann iteriert, bis es fertig ist. Tatsächlich ist man aber in der heutigen Zeit und so auch in Scikit-Learns Standardverhalten schon deutlich weiter: Es wird das durchgeführt, was k-means++ heißt.
K-means++ Initialisierung
Bei k-means++ werden die ursprünglichen Startzentroide nicht rein zufällig in den Raum geworfen, sondern mit einer intelligenten Korrektur, die dafür sorgt, dass die zufälligen Startzentroide nicht durch Pech zu dicht beieinander liegen. Der Algorithmus wählt das erste Zentroid zufällig, aber jedes weitere Zentroid wird mit höherer Wahrscheinlichkeit weit entfernt von bereits gewählten Zentroiden platziert.
Diese Methode führt zu stabileren und besseren Ergebnissen als rein zufällige Initialisierung. Eine exzellente animierte Darstellung dieses Prozesses findest du in diesem Video: K-Means++ Centroid Initialization.
Mehrfache Ausführung mit n_init
Allerdings kann man selbst mit k-means++ noch in bestimmten komplexen Situationen im mehrdimensionalen Raum Pech haben, dass die Startzentroide so ungünstig gefallen sind, dass man an einem lokalen Minimum anlangt - einem finalen Clustering, das aber nicht optimal ist.
Daher führt Scikit-Learn standardmäßig den gesamten K-means-Algorithmus 10-mal mit verschiedenen Startwerten durch (Parameter n_init=10). Diese verschiedenen Startwerte werden jeweils mit der k-means++ Methode optimal gewählt. Nach allen 10 Durchläufen wählt Scikit-Learn automatisch das Ergebnis mit der niedrigsten Inertia aus - also das Clustering mit den kompaktesten Clustern.
Natürlich ist es vor allem bei kleinen Datensätzen nicht selten der Fall, dass alle 10 Durchläufe dieselben Cluster finden. Aber selbst dann hat diese Vorgehensweise abgesehen von der zusätzlichen Rechenzeit ja keine Nachteile.
Vollständiges Clustering: Alle Features
Nachdem wir das Prinzip mit zwei Features verstanden haben, wenden wir K-means auf alle vier verfügbaren Features an. Das Problem dabei: Die Zentroide befinden sich nun im 4-dimensionalen Raum und lassen sich nicht mehr so einfach visualisieren.
# K-means mit allen Features und k=3
kmeans_full = KMeans(n_clusters=3, random_state=42, n_init=10)
cluster_labels_full = kmeans_full.fit_predict(X_scaled)
print(f"K-means Clustering mit allen 4 Features (k=3):")
print(f" Inertia: {kmeans_full.inertia_:.2f}")
print(f" Cluster-Größen: {np.bincount(cluster_labels_full)}")
# Die 4D-Zentroide können wir ausgeben...
print(f"\nZentroide im 4D-Raum:")
centroids_df = pd.DataFrame(
kmeans_full.cluster_centers_,
columns=numeric_features,
index=[f'Cluster {i}' for i in range(3)]
)
print(centroids_df.round(3))
print("\n...aber 4D-Visualisierung ist schwierig!")K-means Clustering mit allen 4 Features (k=3):
Inertia: 379.39
Cluster-Größen: [ 87 123 132]
Zentroide im 4D-Raum:
bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
Cluster 0 0.661 0.817 -0.286 -0.374
Cluster 1 0.657 -1.100 1.159 1.092
Cluster 2 -1.048 0.487 -0.891 -0.771
...aber 4D-Visualisierung ist schwierig!Visualisierungsproblem bei vielen Features
Wir können die Zentroide zwar ausgeben und sehen, dass beispielsweise Cluster 1 durch hohe flipper_length_mm (1.159) und body_mass_g (1.092) charakterisiert ist. Aber eine vollständige Visualisierung im 4D-Raum ist nicht möglich.
Um dennoch eine Visualisierung übers Knie zu brechen, können wir einfach weiterhin nur zwei der vier Features auf die x- und y-Achse packen, die Punkte aber eben so einfärben wie sie im 4-Dimensionalen Raum geclustert wurden:
Code zeigen/verstecken
# Visualisierung mit ersten 2 Features (begrenzte Aussagekraft)
fig, ax = plt.subplots(figsize=(8, 6), layout='tight')
cluster_colors_full = ['#e41a1c', '#377eb8', '#4daf4a']
for i, color in enumerate(cluster_colors_full):
mask = cluster_labels_full == i
ax.scatter(X_scaled[mask, 0], X_scaled[mask, 1],
c=color, label=f'Cluster {i}', alpha=0.7, s=50)
# Zentroide der ersten 2 Features visualisieren
ax.scatter(kmeans_full.cluster_centers_[:, 0], kmeans_full.cluster_centers_[:, 1],
c='black', marker='X', s=200, linewidth=2, label='Zentroide', edgecolor='white')
ax.set_xlabel(f'{numeric_features[0]} (standardisiert)')
ax.set_ylabel(f'{numeric_features[1]} (standardisiert)')
ax.set_title('K-means mit 4 Features\n(nur erste 2 Features visualisiert)')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()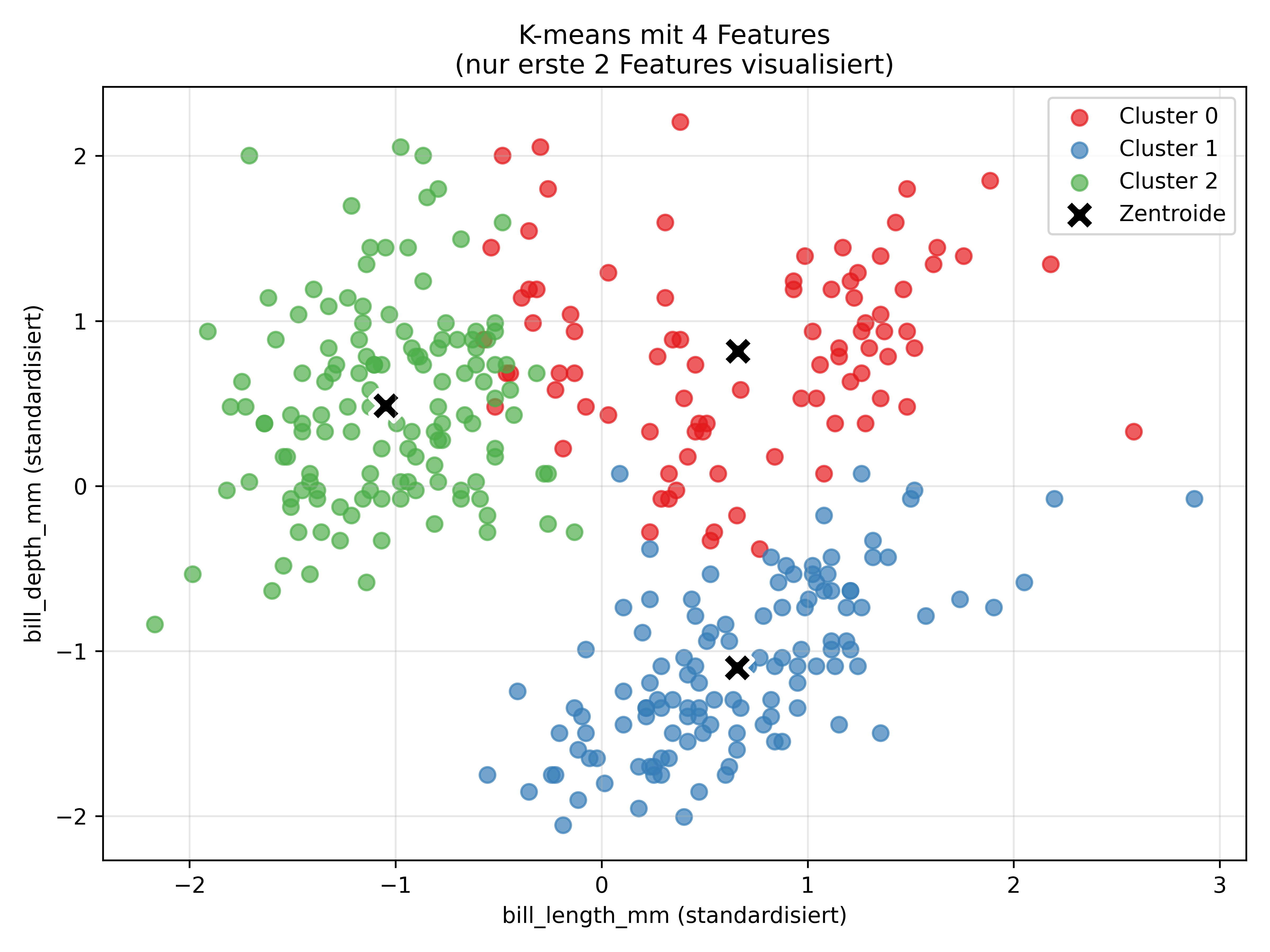
Tatsächlich funktioniert das in speziell diesem Fall noch relativ gut, auch wenn man mehrere Punkte findet, die scheinbar (also in diesem 2D-Raum) dem falschen Cluster zugeordnet wurden.
Allerdings führt uns dies intuitiv mal wieder dazu, dass wir vielleicht erst die Dimensionen reduzieren könnten und zwar mit einer PCA!
PCA + K-means: Ebenfalls ein starkes Team
Abgesehen von unserem Visualisierungsproblem löst die Kombination von PCA und k-means noch zwei wichtige Herausforderungen von k-means:
- Curse of Dimensionality: Bei vielen Features werden Distanzen weniger aussagekräftig
- Effizienz: Weniger Dimensionen bedeuten schnellere Berechnungen
# PCA auf die ersten 2 Komponenten
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)
print(f"PCA Dimensionsreduktion:")
print(f" Ursprünglich: {X_scaled.shape[1]} Features")
print(f" Nach PCA: {X_pca.shape[1]} Hauptkomponenten")
print(f" Erhaltene Varianz: {pca.explained_variance_ratio_.sum():.1%}")
print(f" PC1: {pca.explained_variance_ratio_[0]:.1%}")
print(f" PC2: {pca.explained_variance_ratio_[1]:.1%}")
# K-means auf PCA-transformierten Daten
kmeans_pca = KMeans(n_clusters=3, random_state=42, n_init=10)
cluster_labels_pca = kmeans_pca.fit_predict(X_pca)
print(f"\nK-means Performance-Vergleich:")
print(f" Original Features - Inertia: {kmeans_full.inertia_:.2f}")
print(f" PCA Features - Inertia: {kmeans_pca.inertia_:.2f}")
print(f" Original Features - Silhouette: {silhouette_score(X_scaled, cluster_labels_full):.3f}")
print(f" PCA Features - Silhouette: {silhouette_score(X_pca, cluster_labels_pca):.3f}")PCA Dimensionsreduktion:
Ursprünglich: 4 Features
Nach PCA: 2 Hauptkomponenten
Erhaltene Varianz: 88.2%
PC1: 68.8%
PC2: 19.3%
K-means Performance-Vergleich:
Original Features - Inertia: 379.39
PCA Features - Inertia: 228.33
Original Features - Silhouette: 0.447
PCA Features - Silhouette: 0.539Vollständige Visualisierung mit PCA
Jetzt können wir einen systematischen Vergleich zwischen verschiedenen Ansätzen durchführen. Die folgende umfassende Visualisierung zeigt uns:
- Linke Spalte: Clustering basierend nur auf den ersten 2 Features (Schnabellänge und Schnabeltiefe)
- Rechte Spalte: Clustering basierend auf 2 Hauptkomponenten, die alle 4 Features berücksichtigen
Diese Gegenüberstellung verdeutlicht den Unterschied zwischen einer Analyse mit begrenzten Features und der vollständigen Information durch PCA.
# K-means auf 2 Features
kmeans_2features = KMeans(n_clusters=3, random_state=42, n_init=10)
cluster_labels_2features = kmeans_2features.fit_predict(X_2d_scaled)
# K-means auf 2 Hauptkomponenten basierend auf 4 Features
kmeans_pca_2comp = KMeans(n_clusters=3, random_state=42, n_init=10)
cluster_labels_pca_2comp = kmeans_pca_2comp.fit_predict(X_pca)Code zeigen/verstecken
# Große Figur mit 2 Spalten und 3 Zeilen
fig, axes = plt.subplots(3, 2, figsize=(16, 18), layout='tight')
cluster_colors = ['#e41a1c', '#377eb8', '#4daf4a']
# ===================
# ZEILE 1: Rohdaten
# ===================
# Links: 2 Features, schwarze Punkte
ax = axes[0, 0]
ax.scatter(X_2d_scaled[:, 0], X_2d_scaled[:, 1],
c='black', alpha=0.7, s=50)
ax.set_xlabel(f'{features_2d[0]} (standardisiert)')
ax.set_ylabel(f'{features_2d[1]} (standardisiert)')
ax.set_title('Rohdaten: 2 Features')
ax.grid(True, alpha=0.3)
# Rechts: 2 Hauptkomponenten (basierend auf 4 Features), schwarze Punkte
ax = axes[0, 1]
ax.scatter(X_pca[:, 0], X_pca[:, 1],
c='black', alpha=0.7, s=50)
ax.set_xlabel(f'PC1 ({pca.explained_variance_ratio_[0]:.1%} Varianz)')
ax.set_ylabel(f'PC2 ({pca.explained_variance_ratio_[1]:.1%} Varianz)')
ax.set_title('Rohdaten: 2 Hauptkomponenten\n(basierend auf 4 Features)')
ax.grid(True, alpha=0.3)
# ===================
# ZEILE 2: K-means Clustering
# ===================
# Links: K-means auf 2 Features
ax = axes[1, 0]
for i, color in enumerate(cluster_colors):
mask = cluster_labels_2features == i
ax.scatter(X_2d_scaled[mask, 0], X_2d_scaled[mask, 1],
c=color, label=f'Cluster {i}', alpha=0.7, s=50)
ax.scatter(kmeans_2features.cluster_centers_[:, 0], kmeans_2features.cluster_centers_[:, 1],
c='black', marker='X', s=200, linewidth=2, label='Zentroide', edgecolor='white')
ax.set_xlabel(f'{features_2d[0]} (standardisiert)')
ax.set_ylabel(f'{features_2d[1]} (standardisiert)')
ax.set_title('K-means: 2 Features')
ax.legend()
ax.grid(True, alpha=0.3)
# Rechts: K-means auf 2 Hauptkomponenten
ax = axes[1, 1]
for i, color in enumerate(cluster_colors):
mask = cluster_labels_pca_2comp == i
ax.scatter(X_pca[mask, 0], X_pca[mask, 1],
c=color, label=f'Cluster {i}', alpha=0.7, s=50)
ax.scatter(kmeans_pca_2comp.cluster_centers_[:, 0], kmeans_pca_2comp.cluster_centers_[:, 1],
c='black', marker='X', s=200, linewidth=2, label='Zentroide', edgecolor='white')
ax.set_xlabel(f'PC1 ({pca.explained_variance_ratio_[0]:.1%} Varianz)')
ax.set_ylabel(f'PC2 ({pca.explained_variance_ratio_[1]:.1%} Varianz)')
ax.set_title('K-means: 2 Hauptkomponenten\n(basierend auf 4 Features)')
ax.legend()
ax.grid(True, alpha=0.3)
# ===================
# ZEILE 3: Echte Pinguinarten (zum Vergleich)
# ===================
# Links: 2 Features, eingefärbt nach echten Arten
ax = axes[2, 0]
for species in species_colors.keys():
mask = y_species == species
ax.scatter(X_2d_scaled[mask, 0], X_2d_scaled[mask, 1],
c=species_colors[species], label=species, alpha=0.7, s=50)
ax.set_xlabel(f'{features_2d[0]} (standardisiert)')
ax.set_ylabel(f'{features_2d[1]} (standardisiert)')
ax.set_title('Echte Pinguinarten: 2 Features')
ax.legend()
ax.grid(True, alpha=0.3)
# Rechts: 2 Hauptkomponenten, eingefärbt nach echten Arten
ax = axes[2, 1]
for species in species_colors.keys():
mask = y_species == species
ax.scatter(X_pca[mask, 0], X_pca[mask, 1],
c=species_colors[species], label=species, alpha=0.7, s=50)
ax.set_xlabel(f'PC1 ({pca.explained_variance_ratio_[0]:.1%} Varianz)')
ax.set_ylabel(f'PC2 ({pca.explained_variance_ratio_[1]:.1%} Varianz)')
ax.set_title('Echte Pinguinarten: 2 Hauptkomponenten\n(basierend auf 4 Features)')
ax.legend()
ax.grid(True, alpha=0.3)
plt.show()
Diese umfassende Darstellung zeigt mehrere wichtige Erkenntnisse:
Informationsgehalt: Die rechte Spalte (PCA-basiert) nutzt mit 88% der Gesamtvarianz deutlich mehr Information als die linke Spalte (nur 2 von 4 Features).
Clustering-Qualität: Das PCA-basierte Clustering (mittlere Zeile, rechts) zeigt klarere Trennungen zwischen den Clustern als das Clustering basierend auf nur 2 Features (mittlere Zeile, links).
Biologische Validierung: Die unterste Zeile zeigt die echten Pinguinarten zum Vergleich. Interessant ist, dass sowohl das 2-Feature-Clustering als auch das PCA-Clustering gewisse Ähnlichkeiten zu den biologischen Arten aufweisen, wobei das PCA-Clustering tendenziell bessere Übereinstimmungen zeigt.
Vorteile der PCA+K-means Kombination:
- Vollständige Informationsnutzung: 88% der Varianz aller Features in nur 2 Dimensionen
- Bessere Visualisierbarkeit: Hochdimensionale Cluster können vollständig in 2D dargestellt werden
-
Effizienz: Schnellere Berechnungen durch Dimensionsreduktion
- Robustheit: Weniger anfällig für Rauschen in einzelnen Features
Vor- und Nachteile von K-means
Vorteile:
- Einfach zu verstehen: Intuitives Konzept von “Gruppen um Zentroide”
- Effizient: Schnell auch bei großen Datensätzen
- Skalierbar: Funktioniert gut mit vielen Datenpunkten
- Garantierte Konvergenz: Algorithmus stoppt immer nach endlich vielen Schritten
- Flexibel: Kann mit nachgelagerten Analysen kombiniert werden
Nachteile:
- k muss vorab festgelegt werden: Anzahl Cluster nicht immer bekannt
- Sensitivität der Initialisierung: Kann in lokale Minima geraten (aber k-means++ hilft)
- Annahme sphärischer Cluster: Funktioniert schlecht bei länglichen oder komplexen Cluster-Formen
- Empfindlich für Ausreißer: Zentroide können durch einzelne weit entfernte Punkte verzerrt werden
- Feature Scaling erforderlich: Ohne Standardisierung dominieren Features mit großen Wertebereichen
- Gleiche Cluster-Größen bevorzugt: Tendiert zu Clustern ähnlicher Größe
Alternative Clustering-Methoden
K-means ist nur eine von vielen Clustering-Methoden. Zum Abschluss betrachten wir kurz zwei wichtige Alternativen:
Hierarchisches Clustering
Grundidee: Hierarchisches Clustering baut eine Hierarchie von Clustern auf, entweder von unten nach oben (agglomerativ) oder von oben nach unten (divisiv). Der agglomerative Ansatz ist häufiger: Er startet mit jedem Datenpunkt als eigenem Cluster und verschmilzt schrittweise die beiden ähnlichsten Cluster, bis nur noch ein großer Cluster übrig ist.
Das Ergebnis ist ein Dendrogramm (Baumdiagramm), das alle möglichen Cluster-Anzahlen zeigt. Man kann auf jeder Ebene des Baums “schneiden” und erhält eine andere Anzahl von Clustern - ohne den Algorithmus neu laufen zu lassen.
Stärken:
- Keine Vorab-Festlegung von k nötig - das Dendrogramm zeigt alle Möglichkeiten
-
Zeigt Cluster-Hierarchie und verschiedene Auflösungsebenen
- Deterministisch - gleiche Eingabe führt immer zur gleichen Ausgabe
- Funktioniert mit beliebigen Distanzmaßen
Schwächen:
- Langsamer als k-means - O(n³) statt O(n) Komplexität
- Schwer zu korrigieren bei schlechten frühen Verschmelzungsentscheidungen
- Dendrogramm kann unübersichtlich werden bei großen Datensätzen
Scikit-learn: from sklearn.cluster import AgglomerativeClustering
DBSCAN (Density-Based Spatial Clustering)
Grundidee: DBSCAN findet Cluster basierend auf Punktdichte. Ein Cluster wird als dichte Region von Punkten definiert, die durch weniger dichte Regionen getrennt ist. Der Algorithmus benötigt zwei Parameter: eps (maximaler Abstand zwischen Nachbarn) und min_samples (Mindestanzahl Punkte für einen Cluster).
Punkte werden in drei Kategorien eingeteilt:
-
Core-Punkte: Haben mindestens
min_samplesNachbarn im Radiuseps - Border-Punkte: Liegen im Radius eines Core-Punkts, haben aber selbst zu wenige Nachbarn
- Rauschen-Punkte: Gehören zu keinem Cluster
Stärken:
- Benötigt keine Vorab-Festlegung der Cluster-Anzahl
- Kann Cluster beliebiger Form finden - nicht nur sphärische wie k-means
- Identifiziert automatisch Ausreißer als “Rauschen”
- Robust gegenüber Rauschen in den Daten
Schwächen:
-
Zwei Parameter müssen gewählt werden (
eps,min_samples) - Schwierigkeiten bei Clustern sehr unterschiedlicher Dichte
- Kann bei hochdimensionalen Daten schlecht funktionieren
- Deterministische Reihenfolge kann Randpunkte unterschiedlich zuordnen
Scikit-learn: from sklearn.cluster import DBSCAN
