import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
np.random.seed(42) # für reproduzierbare ErgebnissePräzise Plot-Kontrolle
In der Data Science bewegen wir uns oft zwischen zwei verschiedenen Phasen der Visualisierung: der explorativen Phase, in der wir schnell verschiedene Darstellungen testen und Muster in den Daten entdecken wollen, und der finalen Phase, in der wir Plots für Präsentationen, Berichte oder Publikationen optimieren müssen.
Während in der explorativen Phase Flexibilität und Geschwindigkeit im Vordergrund stehen, erfordern finale Visualisierungen oft eine sehr präzise Kontrolle über jeden Aspekt der Darstellung. Zwei besonders wichtige Bereiche sind dabei die exakte Kontrolle der Plot-Größen und die präzise Steuerung der Achsenbereiche.
In diesem Kapitel lernen wir, wie wir mit matplotlib beide Herausforderungen meistern: Erstens, wie wir das Problem der variablen Größenverhältnisse in IDEs lösen und unsere Plots für den finalen Export optimieren. Zweitens, wie wir die exakte Kontrolle über Achsenlimits und automatische Ränder erlangen, um unsere Visualisierungen pixel-genau anzupassen.
Das Problem mit Größenverhältnissen
Wenn wir mit matplotlib arbeiten, stoßen wir früher oder später auf ein fundamentales Problem: die Größenverhältnisse unserer Plots verhalten sich nicht immer so, wie wir es erwarten würden. Zwar können wir mit figsize die Höhe und Breite des finalen Plots einstellen, doch die tatsächliche visuelle Darstellung hängt auch davon ab, wo und wie wir den Plot betrachten.
Das Problem liegt darin, dass sowohl Jupyter Notebooks als auch andere IDEs wie Positron die Abbildung von einem vorgegebenen Darstellungsbereich einschränken. Einfach ausgedrückt: ziehe ich das Plotfenster in Positron kleiner, so verändern sich auch die Relationen der Elemente in meinem matplotlib-Plot:
Während des explorativen Arbeitsprozesses ist diese Flexibilität gegebenenfalls kein großes Problem. Wir experimentieren mit verschiedenen Visualisierungen, testen unterschiedliche Ansätze und die exakte Darstellung ist noch nicht kritisch.
Geht es jedoch darum, eine Abbildung wirklich final zu optimieren, ist dies selbstverständlich von großem Nachteil. In dieser Phase sind Details wie Schriftgrößen, Abstände, Proportionen und die exakte Positionierung aller Elemente entscheidend. In letzterem Fall ist eine bewährte Möglichkeit, den Plot einfach nach jeder Veränderung zu exportieren und dann außerhalb der IDE zu betrachten - also die exportierte Datei direkt anzuschauen.
Ist das Diagramm so wichtig, dass man an diesen Punkt gelangt, wo man es so feintuned, dann ist es in der Regel sowieso nötig, dass das Diagramm als separate Bilddatei vorliegt, um es an andere senden zu können oder in Präsentationen, Berichte oder wissenschaftliche Arbeiten einzufügen.
Wie schon im Kapitel “6 mehr DataViz > 6.2 Exportieren” aus dem Data Analytics Kurs beschrieben lässt sich dieses Problem z.B. umgehen, indem wir den Plot exportieren und dann außerhalb der IDE betrachten.
Dort haben wir auch gesehen, dass man beispielsweise eine exportierte PNG-Datei mit Python-Befehlen automatisch öffnen kann, um den manuellen Aufwand möglichst gering zu halten.
Eine weitere Alternative ist der Export in eine PDF in Kombination mit einem PDF-Viewer, der es erlaubt und sich automatisch aktualisiert, wenn sich die PDF-Datei ändert. Programme wie Sumatra PDF bleiben geöffnet und zeigen automatisch die neueste Version an, sobald der Plot neu exportiert wurde. (Adobe Acrobat Reader hat diese Funktionalität nicht, da es die Datei sperrt, solange sie geöffnet ist.)
In folgendem gif hat man den direkten Vergleich zwischen dem Plot-Fenster von Positron und der eigentlichen exportierten PDF-Datei wenn man die Werte in figszise ändert:
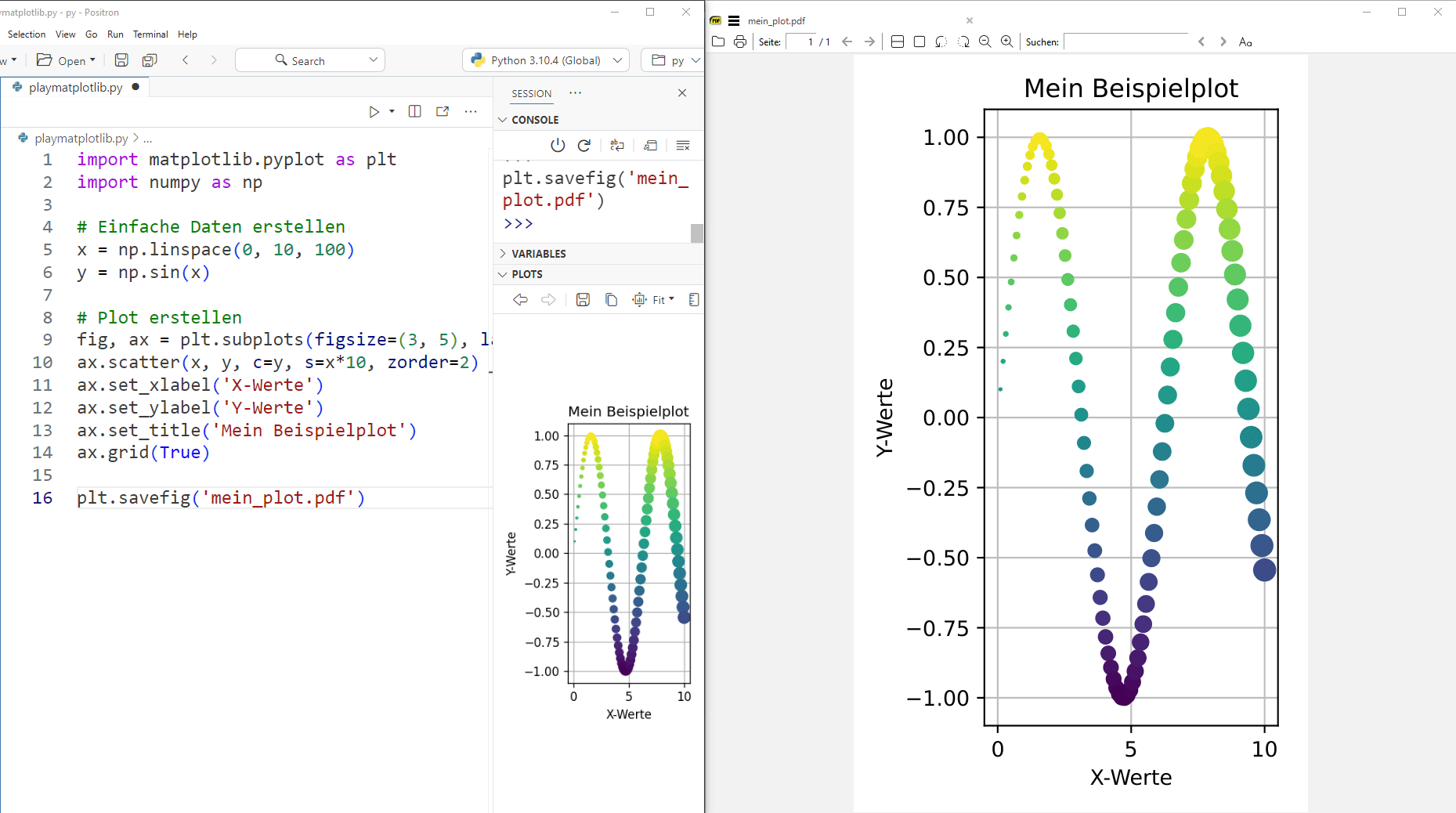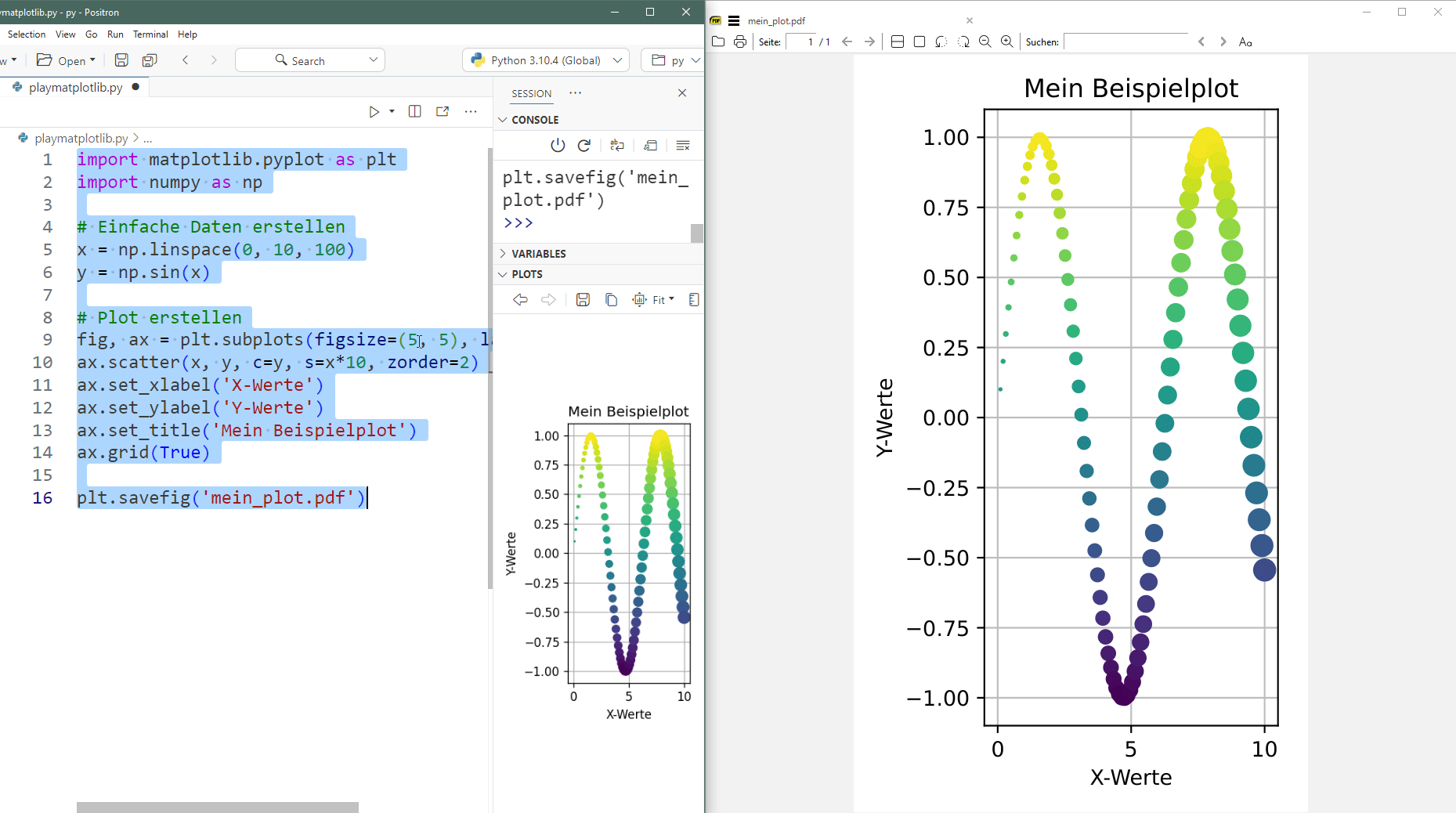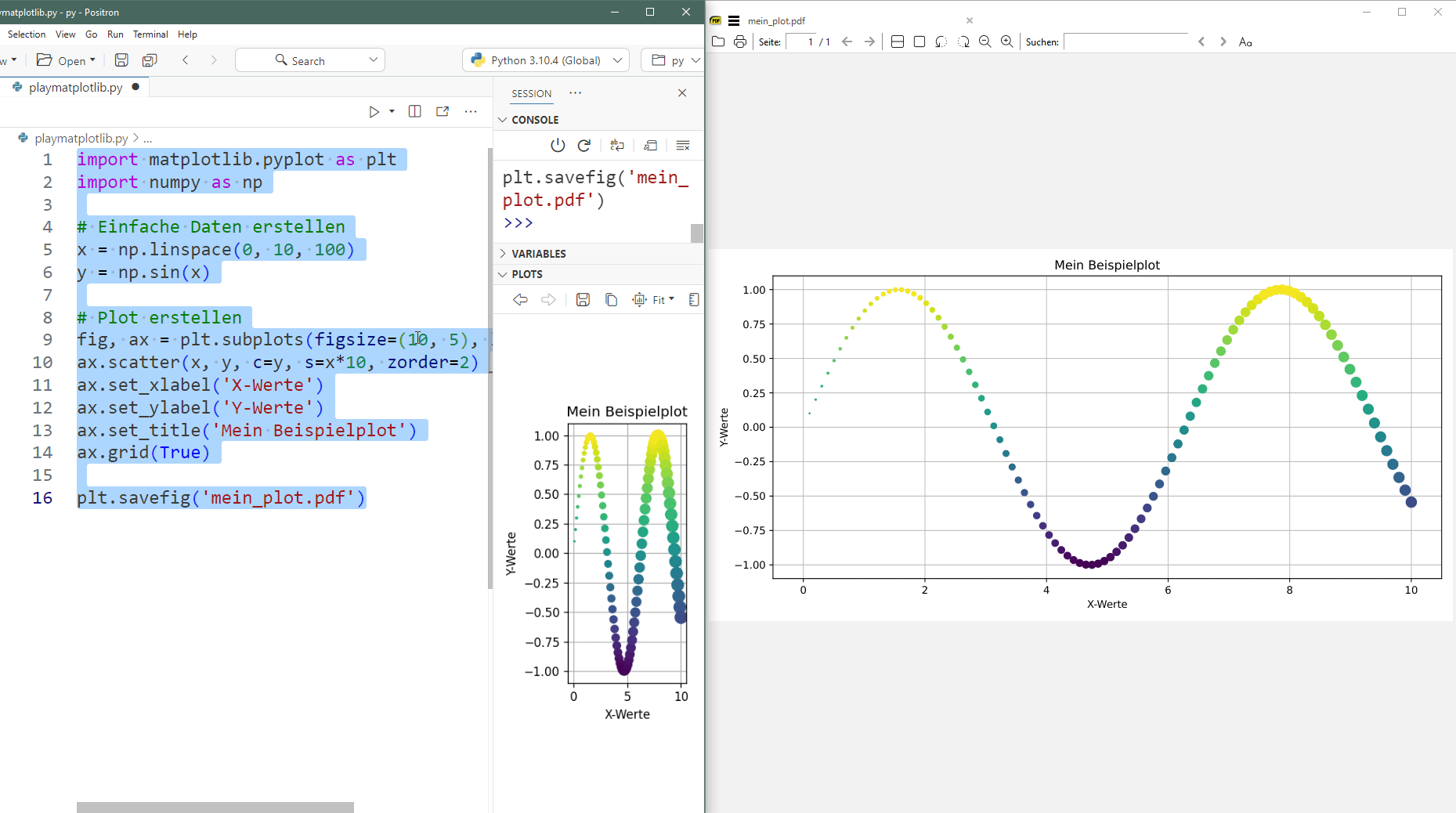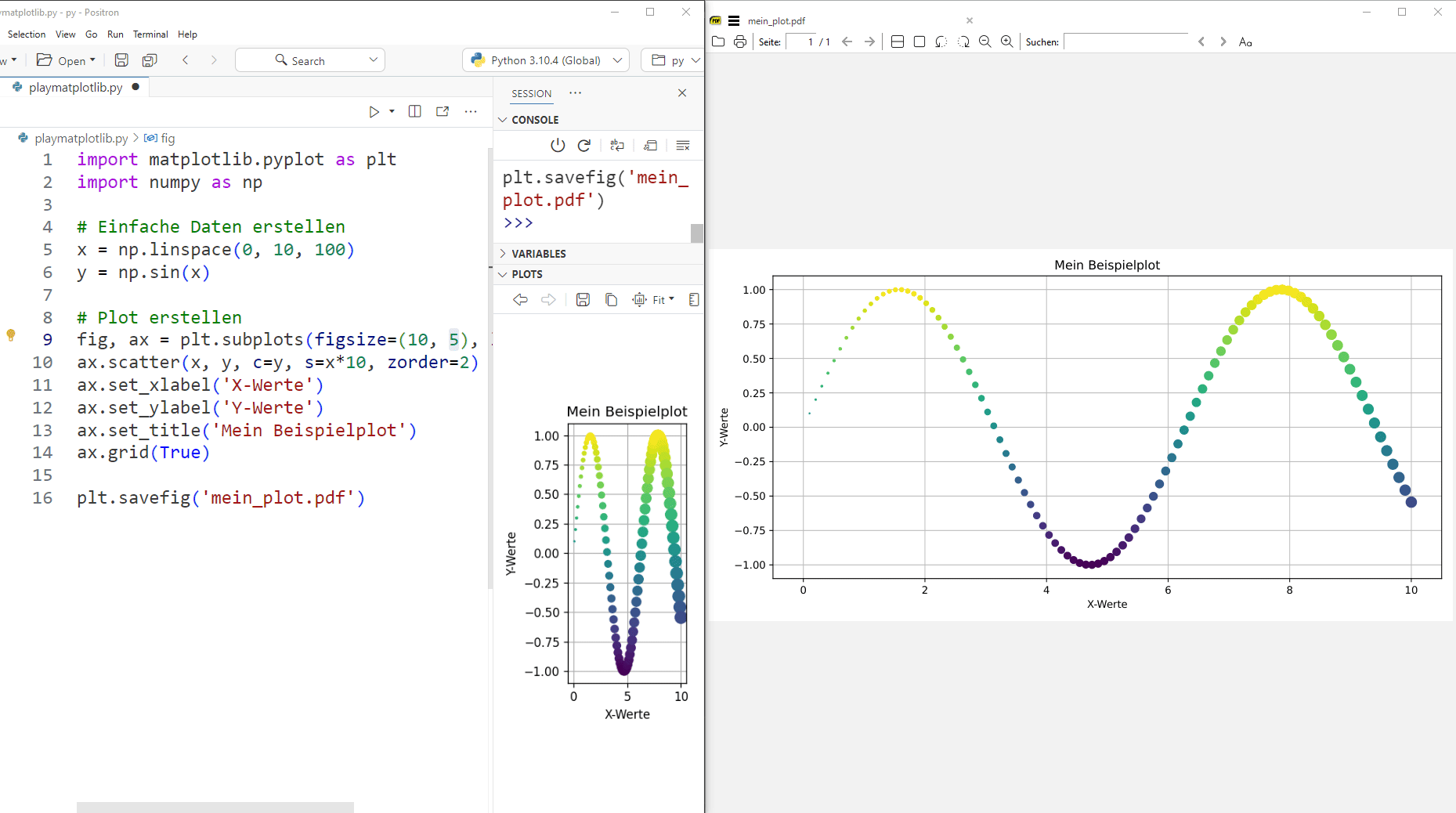
Hier der Code zum selbst ausprobieren:
# Einfache Daten erstellen
x = np.linspace(0, 10, 100)
y = np.sin(x)
# Plot erstellen
fig, ax = plt.subplots(figsize=(6, 5))
ax.scatter(x, y, c=y, s=x*10, zorder=2)
ax.set_xlabel('X-Werte')
ax.set_ylabel('Y-Werte')
ax.set_title('Mein Beispielplot')
ax.grid(True)
plt.show()
plt.savefig('mein_plot.pdf')Achsenlimits und automatische Ränder
Das vorherige Problem mit den Größenverhältnissen ist nur ein Aspekt der präzisen Kontrolle über unsere Plots. Ein weiterer wichtiger Bereich ist die exakte Steuerung darüber, welcher Bereich unserer Daten tatsächlich angezeigt wird und wie viel zusätzlicher Platz um die Daten herum eingefügt wird.
Matplotlib fügt standardmäßig automatisch etwas Platz um unsere Daten ein, damit sie nicht direkt an den Achsen “kleben”. Das ist in den meisten Fällen durchaus sinnvoll - manchmal wollen wir jedoch präzise Kontrolle über diese Aspekte. Hier kommen die Konzepte der Limits (Grenzen der Achsen) und automatische Ränder (zusätzlicher Raum um die Daten) ins Spiel.
Limits: Die Grenzen der Achsen festlegen
Wie wir bereits in Kapitel 4 Deskriptive Statistik 4.4 Punktdiagramme des Data Analyits Kurses gelernt haben, können wir mit set_xlim() und set_ylim() explizit bestimmen, welcher Wertebereich auf den Achsen angezeigt wird. Das ist besonders nützlich, wenn wir den Fokus auf einen bestimmten Bereich legen oder Vergleichbarkeit zwischen mehreren Plots sicherstellen wollen.
# Plot erstellen mit Standard-Grenzen
fig, ax = plt.subplots(figsize=(6, 5))
ax.scatter(x, y, c=y, s=x*10, zorder=2)
ax.set_xlabel('X-Werte')
ax.set_ylabel('Y-Werte')
ax.set_title('Standard-Grenzen')
ax.grid(True)
plt.show()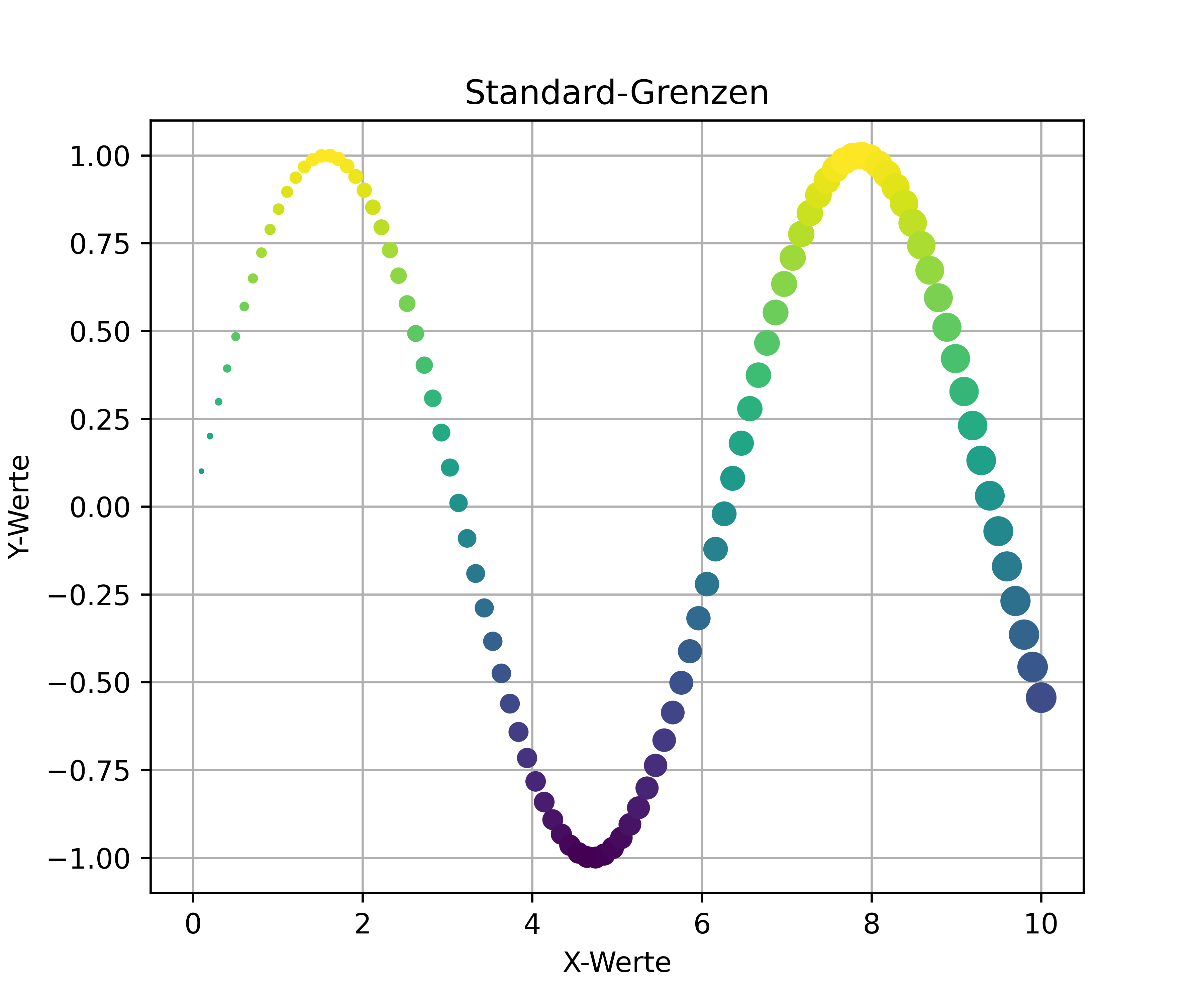
# Plot mit expliziten Grenzen
fig, ax = plt.subplots(figsize=(6, 5))
ax.scatter(x, y, c=y, s=x*10, zorder=2)
ax.set_xlabel('X-Werte')
ax.set_ylabel('Y-Werte')
ax.set_title('Grenzen: X[0,8], Y[-1,2]')
ax.grid(True)
ax.set_xlim(0, 8);
ax.set_ylim(-1, 2);
plt.show()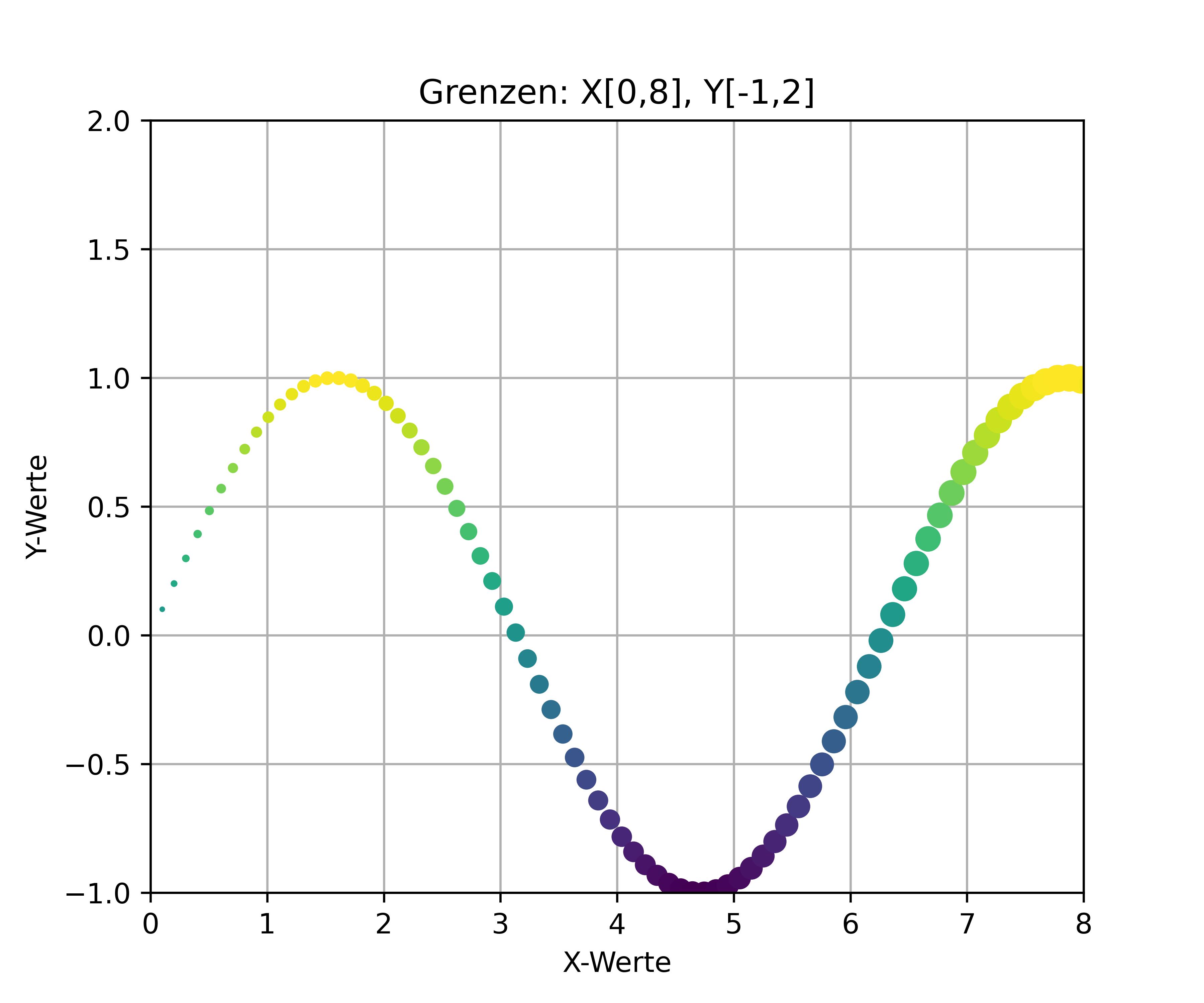
Wir können auch nur eine Seite der Grenze festlegen und die andere automatisch berechnen lassen:
# Plot mit partiellen Grenzen
fig, ax = plt.subplots(figsize=(6, 5))
ax.scatter(x, y, c=y, s=x*10, zorder=2)
ax.set_xlabel('X-Werte')
ax.set_ylabel('Y-Werte')
ax.set_title('Partielle Grenzen: X startet bei 0, Y startet bei 0')
ax.grid(True)
ax.set_xlim(left=0);
ax.set_ylim(bottom=0);
plt.show()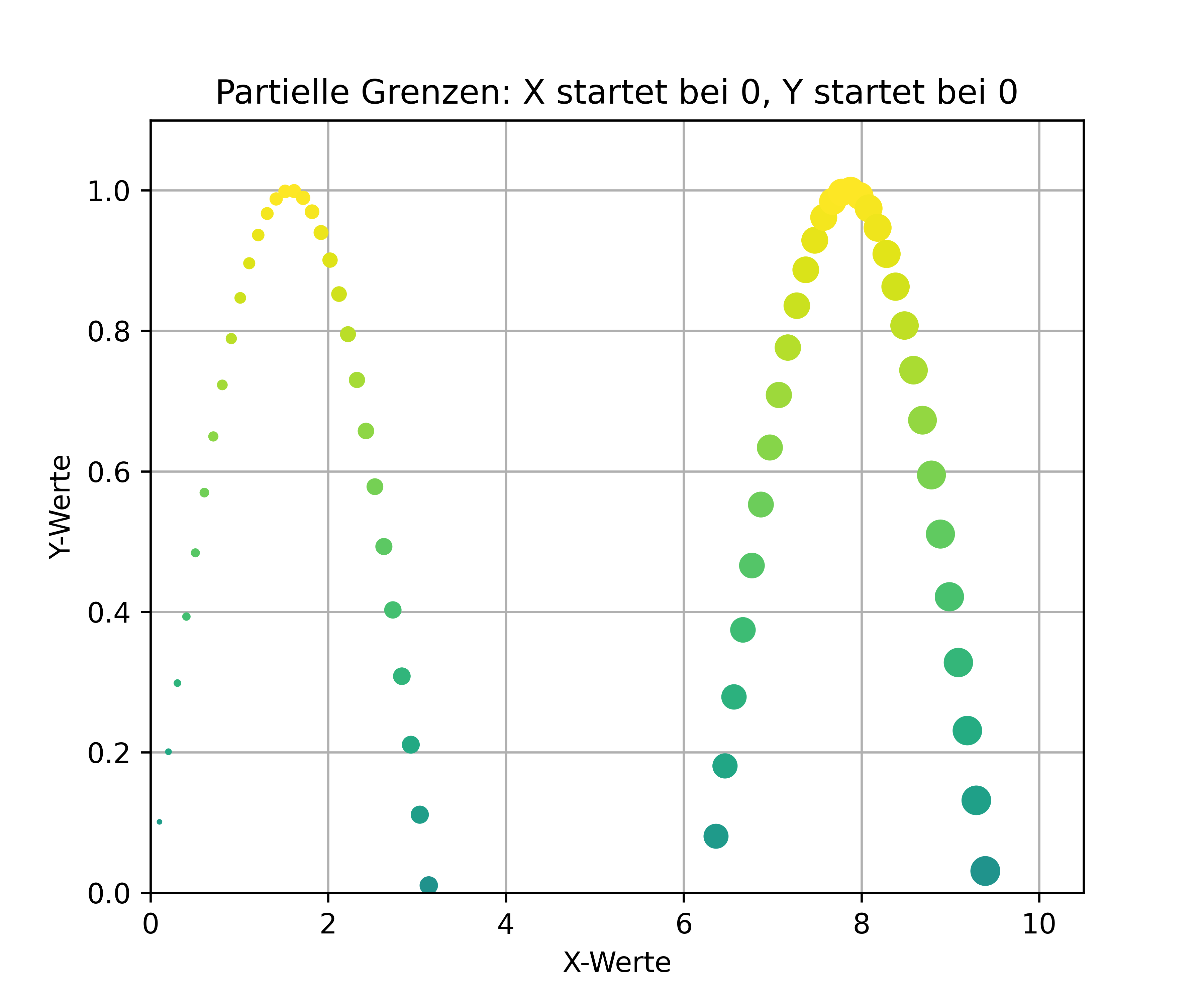
Diese partielle Grenzensetzung ist besonders praktisch, wenn wir beispielsweise sicherstellen wollen, dass die Y-Achse bei 0 beginnt (was bei vielen Datentypen sinnvoll ist), aber den oberen Bereich automatisch anpassen lassen möchten.
Automatische Ränder: Die Margins kontrollieren
Matplotlib fügt standardmäßig automatisch einen kleinen Rand um die Daten ein. Diese automatischen Ränder können wir mit der margins()-Funktion kontrollieren (siehe erster Plot). Wir können auch spezifisch für X- und Y-Achse unterschiedliche Margins setzen (siehe zweiter Plot).
# Plot ohne Expansion
fig, ax = plt.subplots(figsize=(6, 5))
ax.scatter(x, y, c=y, s=x*10, zorder=2)
ax.set_xlabel('X-Werte')
ax.set_ylabel('Y-Werte')
ax.set_title('Keine automatischen Ränder')
ax.grid(True)
ax.margins(0)
plt.show()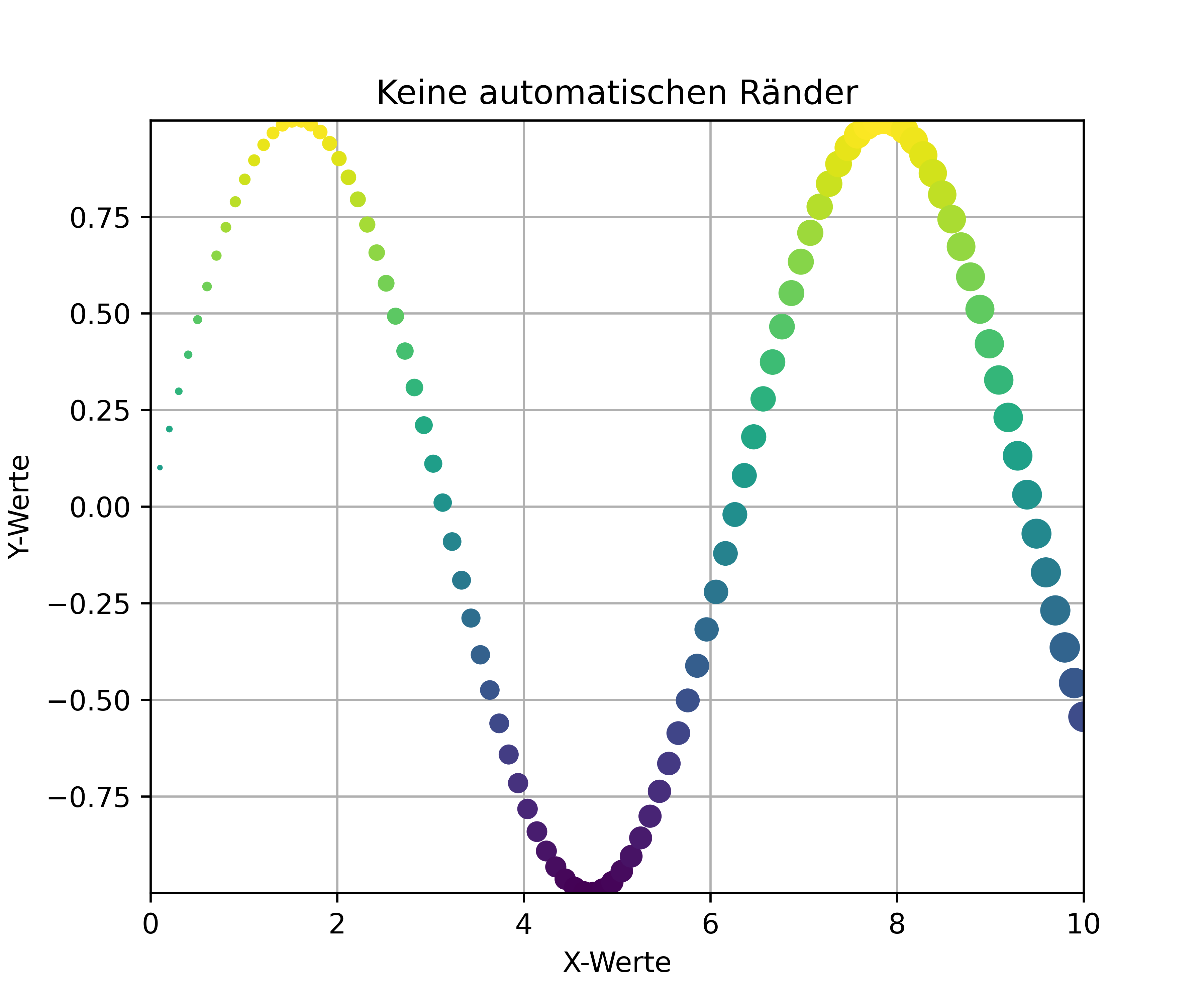
# Plot mit unterschiedlichen Margins
fig, ax = plt.subplots(figsize=(6, 5))
ax.scatter(x, y, c=y, s=x*10, zorder=2)
ax.set_xlabel('X-Werte')
ax.set_ylabel('Y-Werte')
ax.set_title('Unterschiedliche Margins: X=0, Y=0.1')
ax.grid(True)
ax.margins(x=0, y=0.1)
plt.show()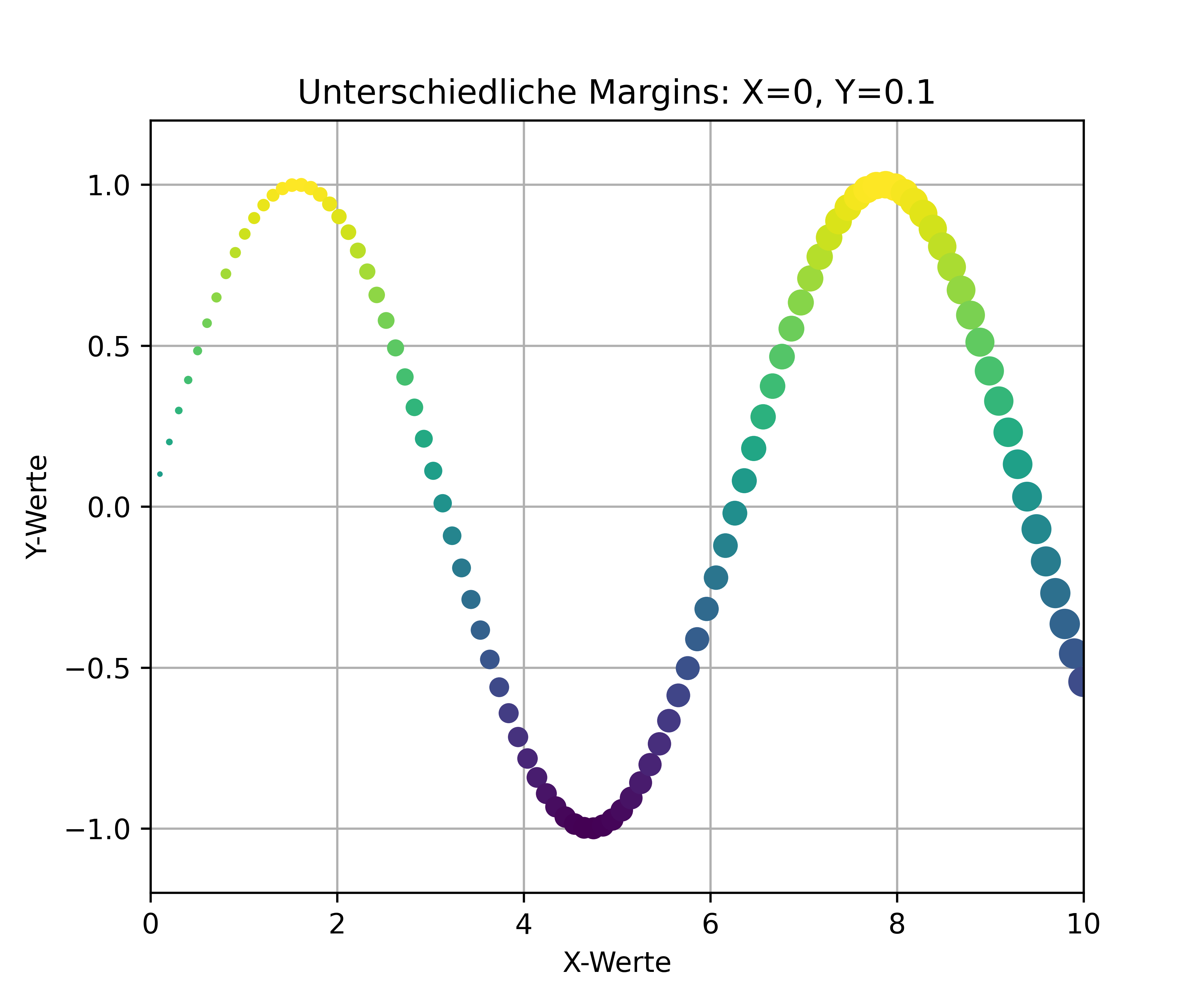
Achtung: Die Reihenfolge zwischen set_xlim() und margins() spielt eine entscheidende Rolle! Schauen wir uns an, was passiert (erster Plot). Der Grund: Sobald wir auch nur eine Seite einer Achse explizit setzen (hier set_xlim(left=0)), ignoriert matplotlib alle nachfolgenden margins()-Befehle für diese gesamte Achse. Das bedeutet, die rechte Grenze wird immer noch mit den Standard-Margins berechnet, und unser margins(0) danach hat gar keine Wirkung mehr (zweiter Plot):
# Falsche Reihenfolge: margins ignoriert
fig, ax = plt.subplots(figsize=(6, 5))
ax.scatter(x, y, c=y, s=x*10, zorder=2)
ax.set_xlabel('X-Werte')
ax.set_ylabel('Y-Werte')
ax.set_title('Problem: margins(0) nach set_xlim(left=0)')
ax.grid(True)
# Diese Reihenfolge funktioniert nicht wie erwartet
ax.set_xlim(left=1);
ax.margins(0);
plt.show()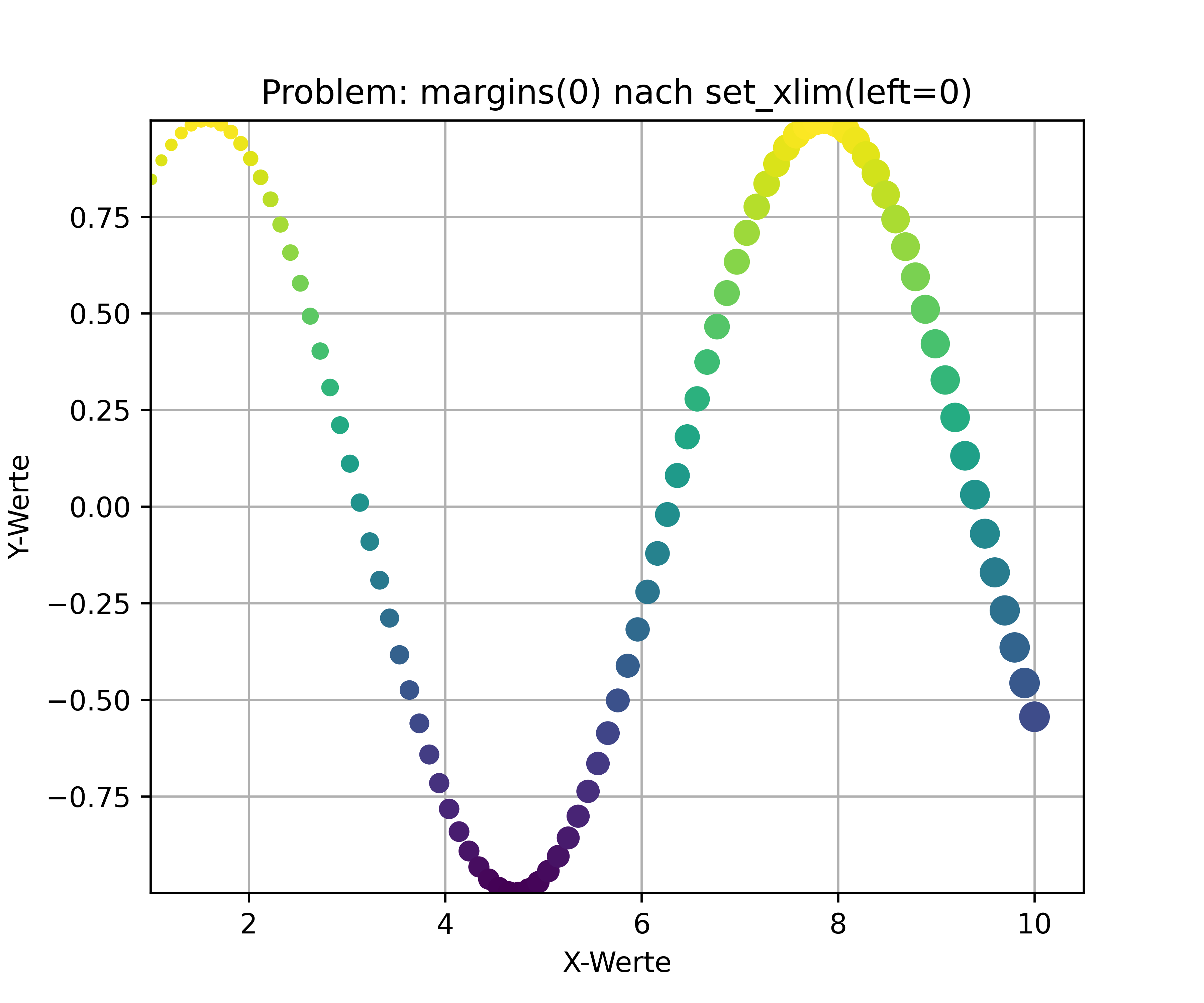
# Richtige Reihenfolge: margins zuerst
fig, ax = plt.subplots(figsize=(6, 5))
ax.scatter(x, y, c=y, s=x*10, zorder=2)
ax.set_xlabel('X-Werte')
ax.set_ylabel('Y-Werte')
ax.set_title('Besser: margins(0) vor set_xlim(left=0)')
ax.grid(True)
# Diese Reihenfolge funktioniert
ax.margins(0);
ax.set_xlim(left=1);
plt.show()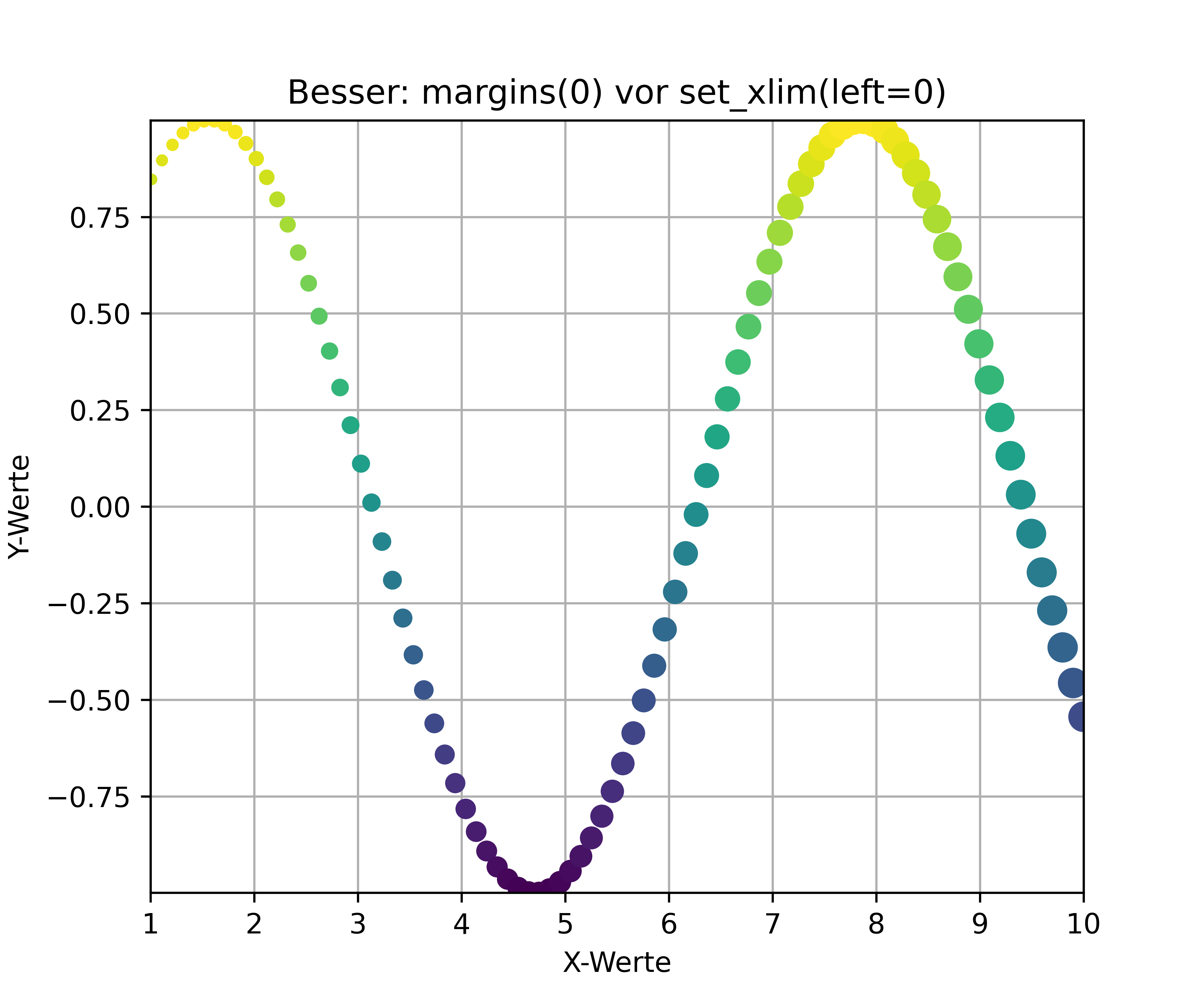
Limits mit Margins kombinieren - nicht so einfach wie erhofft
Schließlich kann man an den Punkt kommen ein bestimmtes Limit setzen zu wollen, aber trotzdem etwas Abstand/Margin um dieses Limit zu haben. Man möchte also beispielsweise, dass die X-Achse bei 5 “beginnt”, aber trotzdem noch etwas Luft links davon hat.
Das Problem: matplotlib macht das nicht automatisch für uns. Wenn wir ax.set_xlim(left=5) setzen, beginnt die Achse exakt bei 5 - ohne jeglichen Abstand und die Margins haben keine Wirkung mehr. Wollen wir trotzdem Abstand, müssen wir das Limit niedriger setzen und selbst berechnen, wo genau. Die quick-and-dirty Lösung wäre also einfach ax.set_xlim(left=4.5) zu setzen, aber das ist natürlich nicht sehr elegant und auch nicht dynamisch.
# Problem: Kein Abstand zum Limit
fig, ax = plt.subplots(figsize=(6, 5))
ax.scatter(x, y, c=y, s=x*10, zorder=2)
ax.set_xlabel('X-Werte')
ax.set_ylabel('Y-Werte')
ax.grid(True)
ax.set_xlim(left=4.5);
plt.show()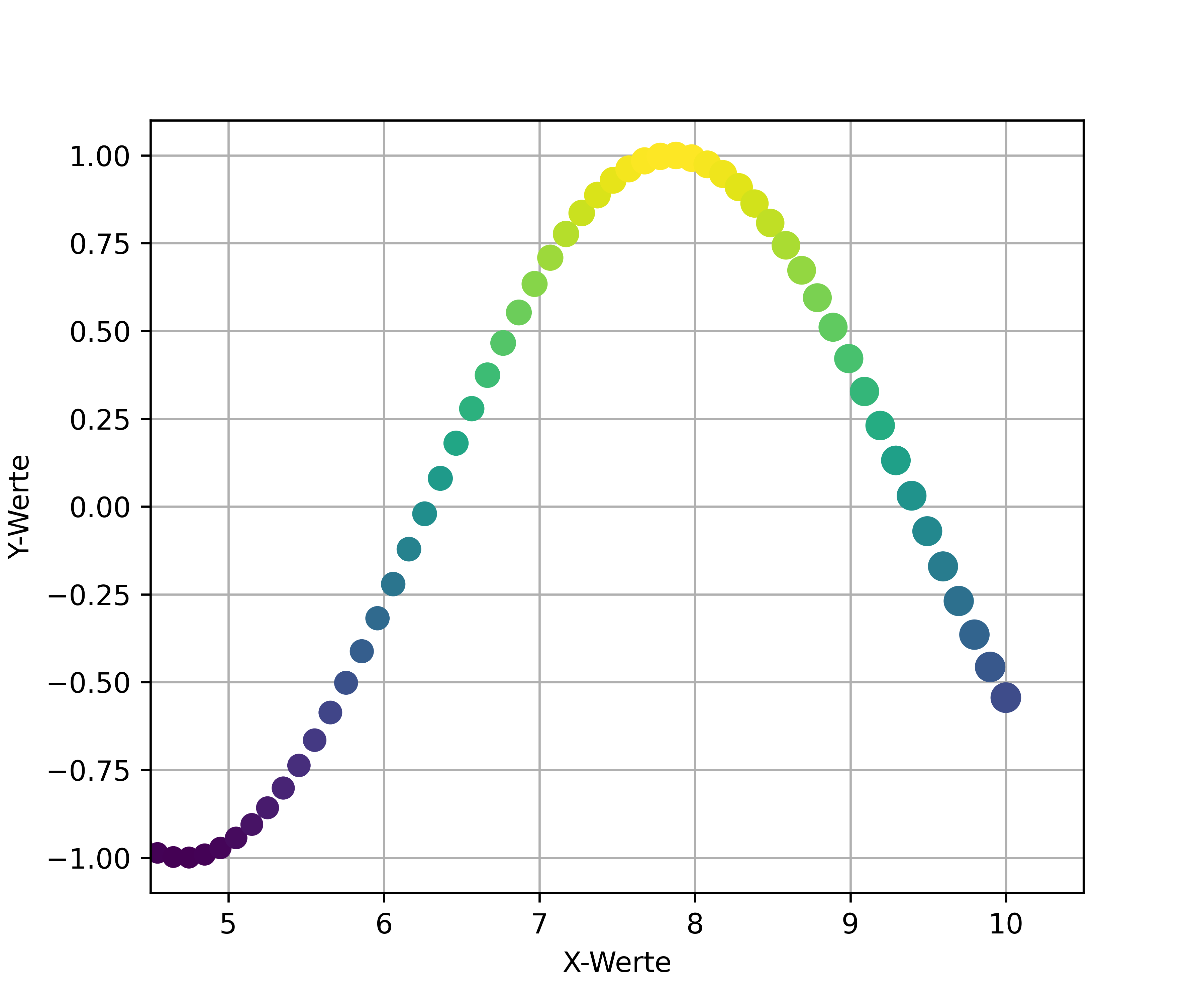
Etwas dynamischer können wir das berechnen, indem wir die Spannweite unserer Daten nutzen und sozusagen ein paar Prozent aufschlagen.
# Gewünschte Limits
gewuenschtes_minimum = 5
gewuenschtes_maximum = max(x)
# Spannweite berechnen
spannweite = gewuenschtes_maximum - gewuenschtes_minimum
# 5% der Spannweite als Abstand
abstand = spannweite * 0.05
fig, ax = plt.subplots(figsize=(6, 5))
ax.scatter(x, y, c=y, s=x*10, zorder=2)
ax.set_xlabel('X-Werte')
ax.set_ylabel('Y-Werte')
ax.set_title('Dynamisch: 5% Abstand zu den Limits')
ax.grid(True)
ax.set_xlim(left=gewuenschtes_minimum - abstand,
right=gewuenschtes_maximum + abstand);
plt.show()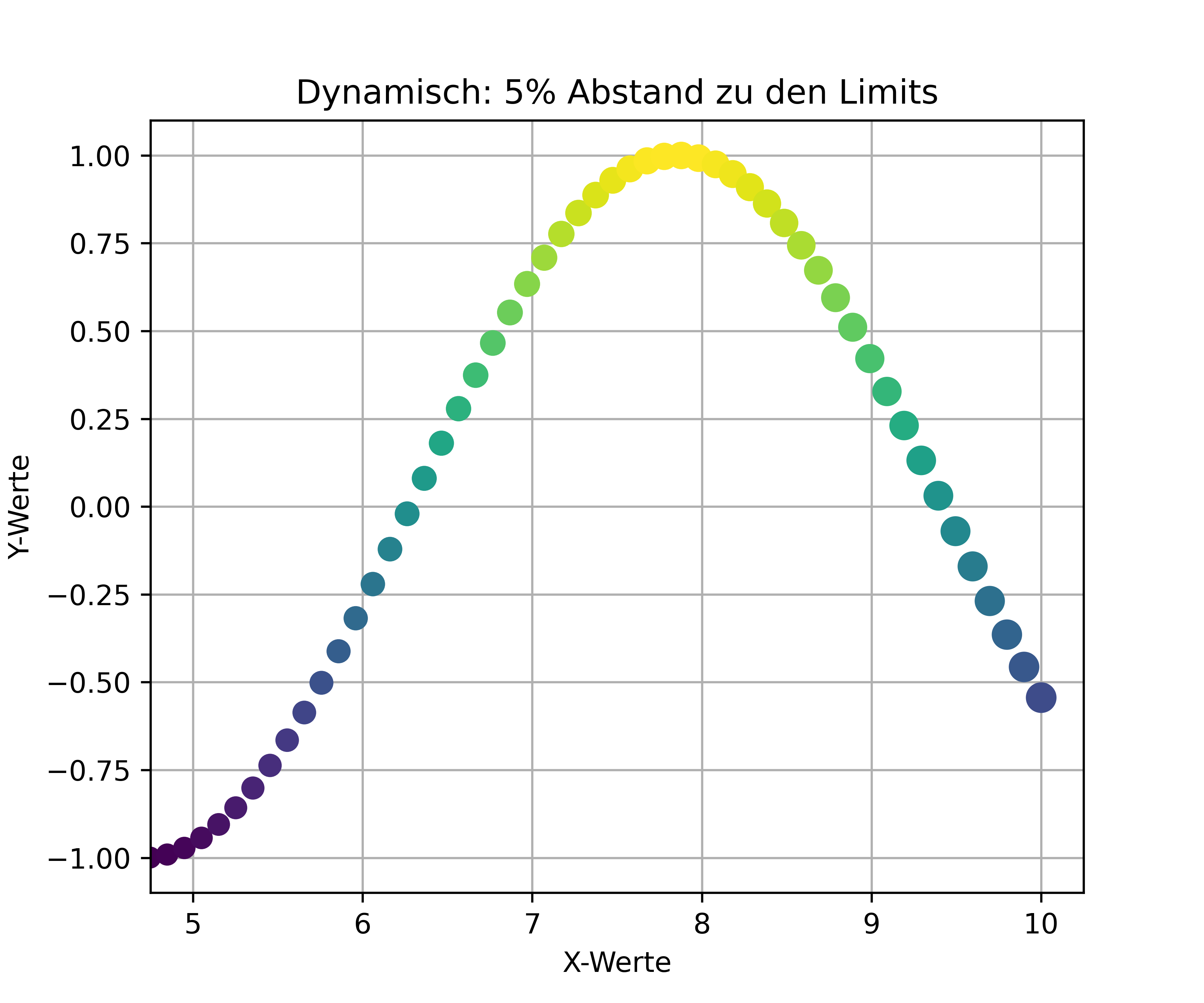
Das ist zugegebenermaßen umständlicher als man vielleicht erwarten würde, aber es gibt uns vollständige Kontrolle über das exakte Verhalten. Man muss eben immer daran denken, dass matplotlib das macht, was wir explizit sagen - es “errät” nicht, dass wir zusätzlichen Abstand wollen.
Diese präzise Kontrolle über Limits und automatische Ränder ist besonders wichtig, wenn wir mehrere Plots vergleichen wollen oder wenn wir sicherstellen müssen, dass bestimmte Werte (wie 0) immer sichtbar sind. In wissenschaftlichen Visualisierungen kann es beispielsweise entscheidend sein, dass Balkendiagramme bei 0 beginnen, um Verzerrungen in der Interpretation zu vermeiden.
Achsentransformationen: Wie Werte dargestellt werden
Bisher haben wir gelernt, welcher Bereich unserer Daten angezeigt wird. Aber manchmal ist auch wichtig, wie die Werte auf den Achsen dargestellt werden. Hier kommen Achsentransformationen ins Spiel - sie verändern die Art und Weise, wie Daten auf den Achsen skaliert werden, ohne die ursprünglichen Datenwerte zu ändern.
Logarithmische Skalierung
Logarithmische Skalen sind besonders nützlich, wenn unsere Daten über mehrere Größenordnungen hinweg variieren oder exponentielles Wachstum zeigen. Statt linearer Abstände zwischen den Werten zeigen logarithmische Skalen konstante Verhältnisse.
Wann braucht man das? Klassische Beispiele sind Bevölkerungswachstum, Aktienkurse, Erdbebenstärken oder jede Art von exponentiellen Prozessen. Auch bei sehr großen Wertebereichen (z.B. von 1 bis 1.000.000) machen logarithmische Skalen Muster sichtbar, die sonst untergehen würden.
# Exponentielles Wachstum simulieren
jahre = np.arange(1990, 2025)
bevoelkerung = 1000 * (1.20 ** (jahre - 1990)) # 20% Wachstum pro Jahr
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), layout='tight')
# Lineare Skalierung
ax1.plot(jahre, bevoelkerung, 'b-o', markersize=4)
ax1.set_title('Bevölkerungswachstum (linear)')
ax1.set_xlabel('Jahr')
ax1.set_ylabel('Bevölkerung')
ax1.grid(True)
# Logarithmische Skalierung
ax2.plot(jahre, bevoelkerung, 'r-o', markersize=4)
ax2.set_yscale('log')
ax2.set_title('Bevölkerungswachstum (logarithmisch)')
ax2.set_xlabel('Jahr')
ax2.set_ylabel('Bevölkerung (log)')
ax2.grid(True)
plt.show()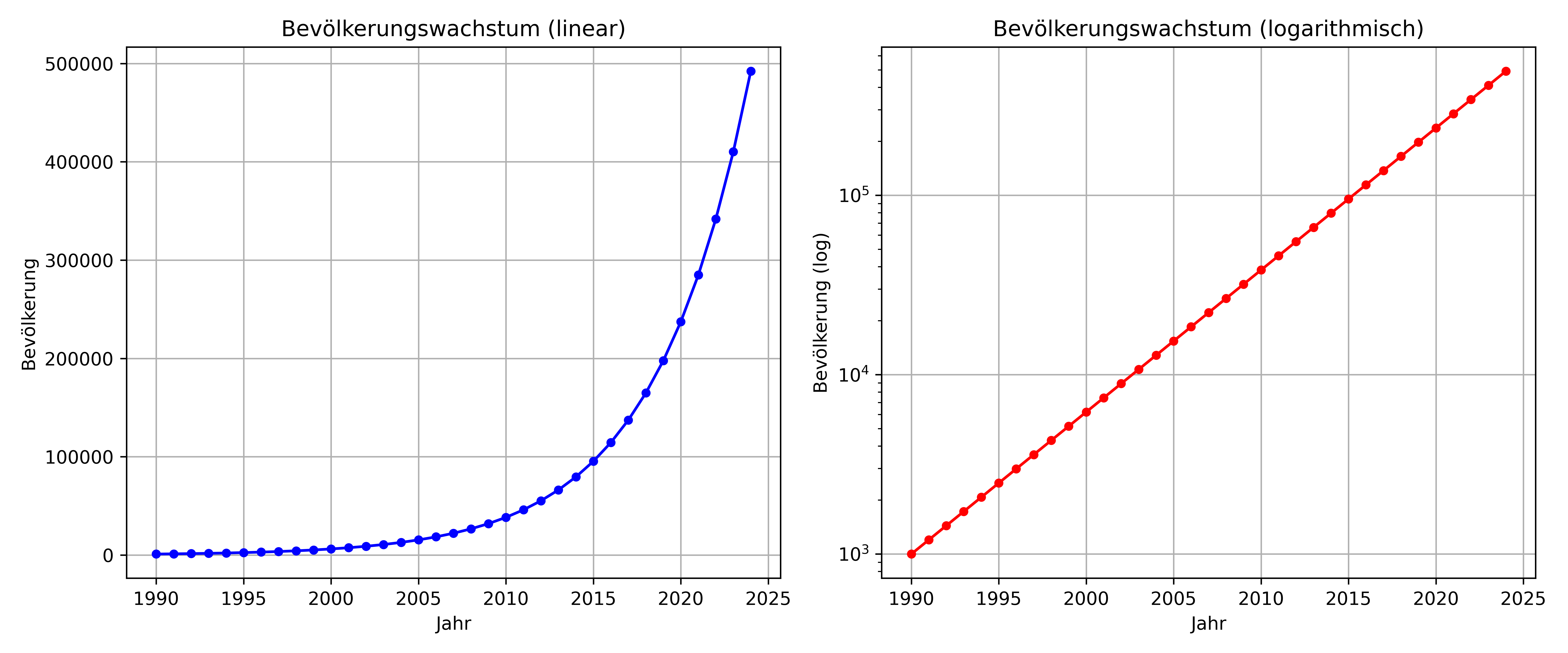
Achtung: Logarithmische Skalen können nicht mit Null oder negativen Werten umgehen! Das liegt prinzipiell daran, dass der Logarithmus von Null Minus unendlich und der Logarithmus von negativen Zahlen nicht definiert ist. Im Folgenden Beispielplot setzen wir deshalb die ersten zwei Werte auf -2 und 0 und sehen, dass matplotlib diese schlichtweg nicht anzeigt, sondern die Achse bei knapp über 0 beginnt. Tatsächlich hat man sogar mit dem Argument nonpostive noch die Wahl wie mit nicht-positiven Werten 0 umgegangen werden soll.
Die set_yscale('log') Funktion bietet mehrere nützliche Parameter zur Anpassung:
-
base: Ändert die Logarithmus-Basis (z.B. 2 für binär, 10 für dezimal) -
subs: Kontrolliert die Platzierung der Minor Ticks zwischen Major Ticks -
nonpositive: Bestimmt den Umgang mit nicht-positiven Werten-
'mask': Nicht-positive Werte werden ignoriert und nicht geplottet -
'clip': Nicht-positive Werte werden durch einen sehr kleinen positiven Wert ersetzt
-
# Daten mit problematischen Werten
problematische_daten = [-2, 0, 1, 4, 16, 64, 256, 1024]
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), layout='tight')
# Basis 2 mit 'mask' für nicht-positive Werte
ax1.plot(range(len(problematische_daten)), problematische_daten, 'bo-', markersize=6)
ax1.set_yscale('log', base=2, nonpositive='mask')
ax1.set_title("Log-Basis 2, nonpositive='mask'")
ax1.set_ylabel('Werte (log₂)')
ax1.grid(True, which='both', alpha=0.3)
# Basis 10 mit 'clip' für nicht-positive Werte
ax2.plot(range(len(problematische_daten)), problematische_daten, 'ro-', markersize=6)
ax2.set_yscale('log', base=10, nonpositive='clip')
ax2.set_title("Log-Basis 10, nonpositive='clip'")
ax2.set_ylabel('Werte (log₁₀)')
ax2.grid(True, which='both', alpha=0.3)
plt.show()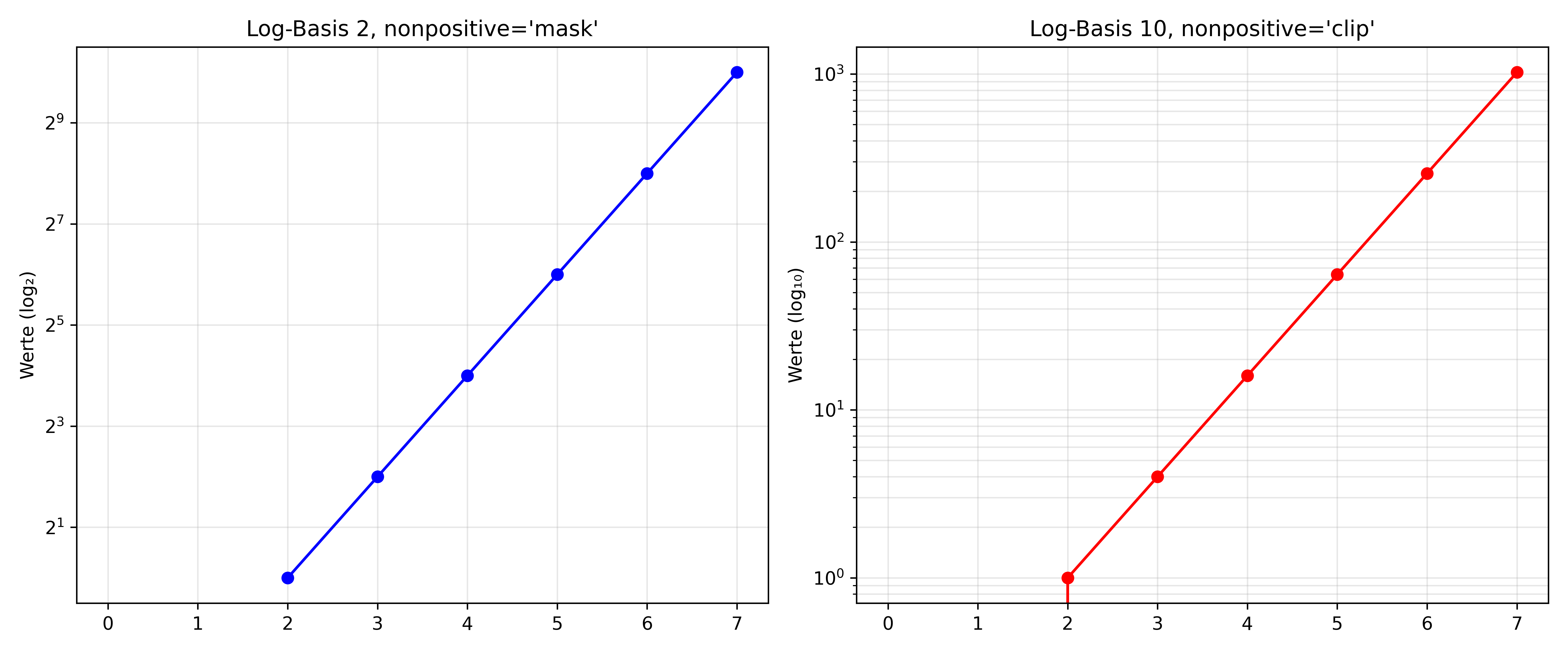
Symmetrisch-logarithmische Skalierung (symlog)
Die symlog Skalierung ist eine Alternative, welche lineare Skalierung um Null herum mit logarithmischer Skalierung für große Beträge kombiniert.
Wann braucht man das? Bei Daten, die sowohl positive als auch negative Werte haben und dabei große Bereiche abdecken. Beispielsweise Temperaturanomalien, Finanzgewinne/-verluste oder physikalische Messungen mit Nulldurchgang.
Parameter für symlog (zusätzlich zu denen für log):
-
linthresh: Bestimmt den Bereich um Null, der linear skaliert wird -
linscale: Kontrolliert die relative Größe des linearen Bereichs im Verhältnis zum logarithmischen Bereich
x_data = np.linspace(-100, 100, 500)
y_data = x_data ** 3 + np.random.normal(0, 10, 500)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), layout='tight')
ax1.scatter(x_data, y_data, alpha=0.6)
ax1.set_yscale('symlog', linthresh=1, linscale=1)
ax1.set_title('linthresh=1, linscale=1')
ax1.set_xlabel('X-Werte')
ax1.set_ylabel('Y-Werte (symlog)')
ax1.grid(True)
ax2.scatter(x_data, y_data, alpha=0.6)
ax2.set_yscale('symlog', linthresh=100, linscale=3)
ax2.set_title('linthresh=100, linscale=3')
ax2.set_xlabel('X-Werte')
ax2.set_ylabel('Y-Werte (symlog)')
ax2.grid(True)
plt.show()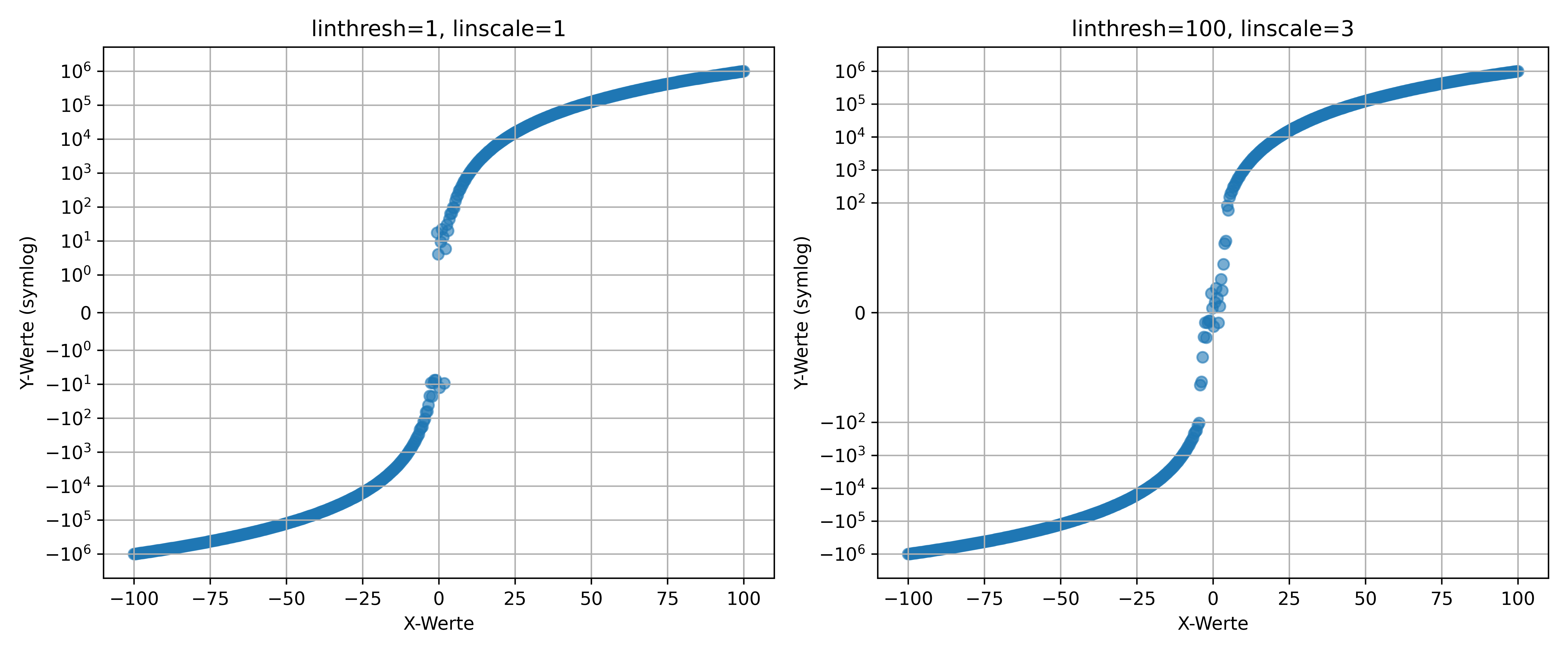
Interpretation: Bei linthresh=1 werden Werte zwischen -1 und +1 linear dargestellt, darüber und darunter logarithmisch. Der linscale Parameter bestimmt, wie viel visueller Raum der lineare Bereich im Verhältnis zum logarithmischen Bereich einnimmt.
Aufgabe 1
Bei einer Präsidentschaftswahl haben zwei Kandidaten folgende Ergebnisse erzielt:
- Kandidat A: 49% der Stimmen
- Kandidat B: 51% der Stimmen
Hier ist der Grundcode für ein Diagramm:
import matplotlib.pyplot as plt
# Daten
kandidaten = ['Kandidat A', 'Kandidat B']
stimmen = [49, 51]
# Einfaches Balkendiagramm
fig, ax = plt.subplots(figsize=(8, 6))
ax1.scatter(kandidaten, stimmen, s=100)
ax.set_ylabel('Stimmenanteil (%)')
ax.set_title('Wahlergebnisse')
plt.show()Modifiziere den Code so, dass zwei Diagramme nebeneinander mit
plt.subplots()erstellt werden. Das erste Diagramm soll genau wie oben aussehen, das zweite soll identisch sein, aber die Y-Achse soll explizit bei 0 beginnen und bei 100 aufhören.Betrachte beide Plots und beantworte: Was fällt dir beim visuellen Eindruck auf? Welcher Plot vermittelt einen faireren Eindruck der tatsächlichen Verhältnisse?