import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import statsmodels.formula.api as smf
import scipy.stats as stats
np.random.seed(42) # für reproduzierbare ErgebnisseANCOVA und Moderationsanalyse
In den vorangegangenen Kapiteln haben wir verschiedene statistische Modelle kennengelernt: Modelle mit einer oder mehreren kategorischen Variablen (t-Test, ANOVA), sowie Modelle mit einer oder mehreren metrischen Variablen (einfache und multiple lineare Regression, Polynomregression). Doch natürlich kann es auch vorkommen, dass wir beide Arten von Variablen in einem Modell kombinieren möchten.
Genau diese Kombination ist der Fokus dieses Kapitels. Wir werden zwei verwandte Ansätze kennenlernen: die ANCOVA (Analysis of Covariance) und die Moderationsanalyse. Der entscheidende Unterschied zwischen beiden liegt darin, ob die kategorische und die metrische Variable miteinander interagieren oder nicht.
Ein Beispiel zur Motivation
Betrachten wir zunächst ein Beispiel aus dem Palmer Penguins Datensatz. Stellen wir uns vor, wir interessieren uns für den Zusammenhang zwischen der Schnabeltiefe (bill_depth_mm) und dem Körpergewicht (body_mass_g):
# Palmer Penguins Datensatz laden
csv_url = 'https://raw.githubusercontent.com/SchmidtPaul/ExampleData/refs/heads/main/palmer_penguins/palmer_penguins.csv'
penguins = pd.read_csv(csv_url)
# Definiere Farben für die Pinguinarten
colors = {'Adelie': '#FF8C00', 'Chinstrap': '#A034F0', 'Gentoo': '#159090'}
# Daten für die Analyse vorbereiten
penguins_clean = penguins[['body_mass_g', 'bill_depth_mm', 'species']].dropna()
Wenn wir zunächst wirklich nur diese beiden Variablen betrachten, können wir eine Regressionsgerade wie folgt anpassen:
Code zeigen/verstecken
# Erster Plot: Ohne Berücksichtigung der Arten
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
# Alle Datenpunkte ohne Farbunterscheidung
ax.scatter(penguins_clean['bill_depth_mm'], penguins_clean['body_mass_g'],
alpha=0.6, color='gray', s=50)
# Einfache Regressionsgerade über alle Daten
model_simple = smf.ols('body_mass_g ~ bill_depth_mm', data=penguins_clean).fit()
x_range = np.linspace(penguins_clean['bill_depth_mm'].min(),
penguins_clean['bill_depth_mm'].max(), 100)
y_pred = model_simple.predict(pd.DataFrame({'bill_depth_mm': x_range}))
ax.plot(x_range, y_pred, color='red', linewidth=2,
label=f'Einfache Regression (R² = {model_simple.rsquared:.3f})')
ax.set_xlabel('Schnabeltiefe (mm)')
ax.set_ylabel('Körpergewicht (g)')
ax.set_title('Zusammenhang ohne Berücksichtigung der Pinguinarten')
ax.legend()
plt.show()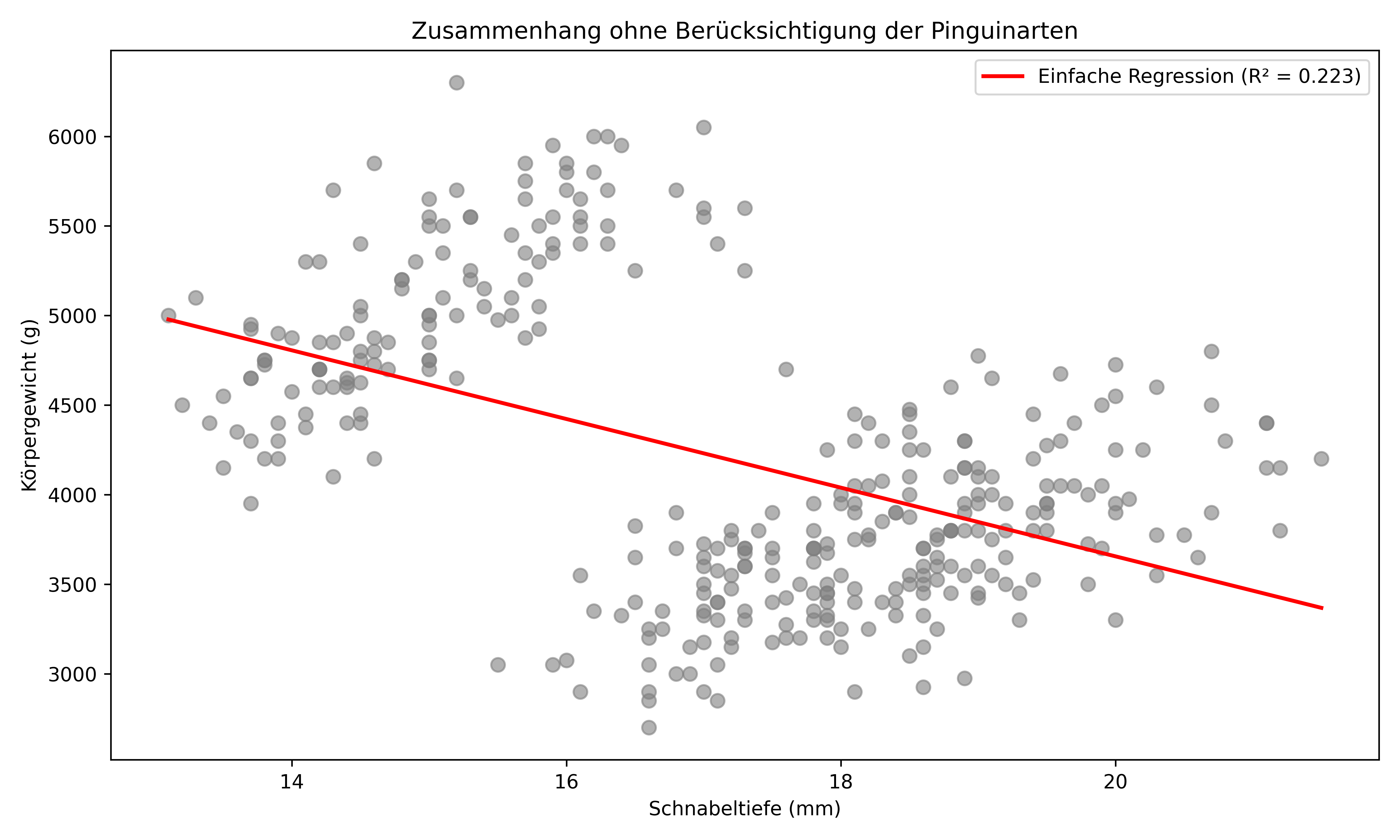
Die einfache lineare Regression zeigt zwar einen schwachen Zusammenhang, doch schon mit dem bloßen Augen wirken die Punkte eigenartig verteilt. Das ganze klärt sich schnell auf, wenn wir die Pinguinarten berücksichtigen. Hier ist bereits ein Vorgeschmack auf das, was wir am Ende dieses Kapitels erreichen werden:
Code zeigen/verstecken
# Zweiter Plot: Mit Berücksichtigung der Arten (Vorschau)
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
# Datenpunkte nach Arten gefärbt
for species in penguins_clean['species'].unique():
data = penguins_clean[penguins_clean['species'] == species]
ax.scatter(data['bill_depth_mm'], data['body_mass_g'],
alpha=0.7, color=colors[species], s=50, label=species)
# Separate Regressionsgeraden für jede Art (Moderationsanalyse)
for species in penguins_clean['species'].unique():
data = penguins_clean[penguins_clean['species'] == species]
if len(data) > 1: # Nur wenn genügend Datenpunkte vorhanden
model_species = smf.ols('body_mass_g ~ bill_depth_mm', data=data).fit()
x_range_species = np.linspace(data['bill_depth_mm'].min(),
data['bill_depth_mm'].max(), 100)
y_pred_species = model_species.predict(pd.DataFrame({'bill_depth_mm': x_range_species}))
ax.plot(x_range_species, y_pred_species, color=colors[species],
linewidth=2, linestyle='--')
ax.set_xlabel('Schnabeltiefe (mm)')
ax.set_ylabel('Körpergewicht (g)')
ax.set_title('Zusammenhang mit Berücksichtigung der Pinguinarten')
ax.legend()
plt.show()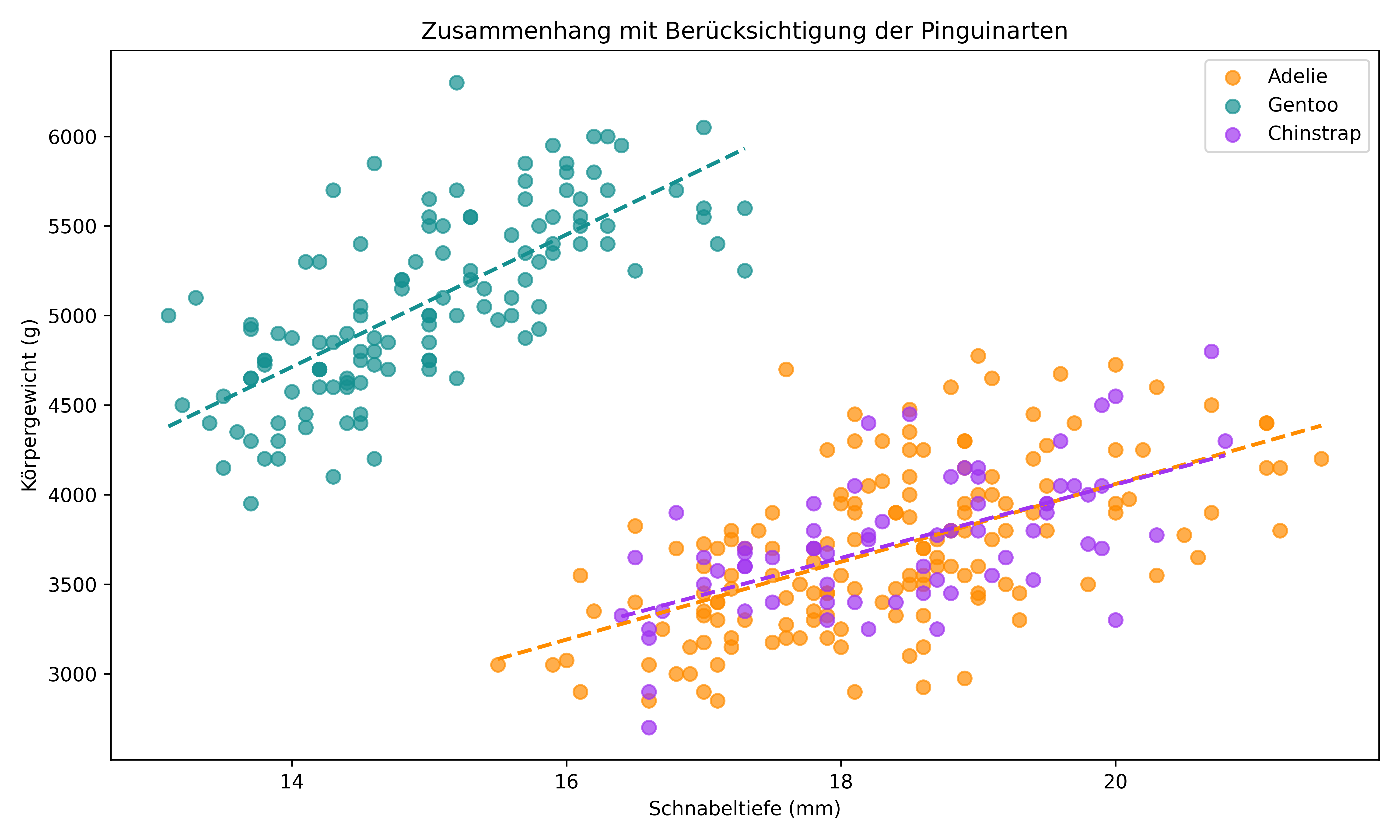
Die Unterschiede sind dramatisch! Statt eines schwach negativen Gesamtzusammenhangs sehen wir nun drei verschiedene Beziehungen für die drei Pinguinarten. Jede Art hat nicht nur eine andere Steigung, sondern auch einen anderen Achsenabschnitt. Alle drei Steigungen sind im Gegensatz zur Steigung davor positiv
Dies zeigt uns, dass die Pinguinart den Zusammenhang zwischen Schnabeltiefe und Körpergewicht moderiert - ein klassischer Fall für eine Moderationsanalyse. Aber der Reihe nach: Beginnen wir zunächst mit der ANCOVA.
Teil 1: ANCOVA (Analysis of Covariance)
Die ANCOVA (Analysis of Covariance) kombiniert die Varianzanalyse (ANOVA) mit der linearen Regression. Sie ermöglicht es uns, Gruppenunterschiede zu untersuchen, während wir gleichzeitig für eine Kovariable (eine metrische Variable) kontrollieren.
Der mtcars Datensatz
Für unsere ANCOVA verwenden wir den klassischen mtcars Datensatz, der verschiedene Eigenschaften von Automobilen aus den 1970er Jahren enthält:
# mtcars Datensatz laden
mtcars = sm.datasets.get_rdataset('mtcars').data
# Relevante Variablen extrahieren und vorbereiten
mtcars_clean = mtcars[['mpg', 'am', 'hp']].copy()
# Faktor-Variable für bessere Lesbarkeit umkodieren
mtcars_clean['transmission'] = mtcars_clean['am'].map({0: 'Automatik', 1: 'Manuell'})
# Definiere Farben für die Getriebearten
transmission_colors = {'Automatik': '#00923f', 'Manuell': '#ad0000'}
mtcars_clean mpg am hp transmission
rownames
Mazda RX4 21.0 1 110 Manuell
Mazda RX4 Wag 21.0 1 110 Manuell
Datsun 710 22.8 1 93 Manuell
Hornet 4 Drive 21.4 0 110 Automatik
Hornet Sportabout 18.7 0 175 Automatik
Valiant 18.1 0 105 Automatik
Duster 360 14.3 0 245 Automatik
Merc 240D 24.4 0 62 Automatik
Merc 230 22.8 0 95 Automatik
Merc 280 19.2 0 123 Automatik
Merc 280C 17.8 0 123 Automatik
Merc 450SE 16.4 0 180 Automatik
Merc 450SL 17.3 0 180 Automatik
Merc 450SLC 15.2 0 180 Automatik
Cadillac Fleetwood 10.4 0 205 Automatik
Lincoln Continental 10.4 0 215 Automatik
Chrysler Imperial 14.7 0 230 Automatik
Fiat 128 32.4 1 66 Manuell
Honda Civic 30.4 1 52 Manuell
Toyota Corolla 33.9 1 65 Manuell
Toyota Corona 21.5 0 97 Automatik
Dodge Challenger 15.5 0 150 Automatik
AMC Javelin 15.2 0 150 Automatik
Camaro Z28 13.3 0 245 Automatik
Pontiac Firebird 19.2 0 175 Automatik
Fiat X1-9 27.3 1 66 Manuell
Porsche 914-2 26.0 1 91 Manuell
Lotus Europa 30.4 1 113 Manuell
Ford Pantera L 15.8 1 264 Manuell
Ferrari Dino 19.7 1 175 Manuell
Maserati Bora 15.0 1 335 Manuell
Volvo 142E 21.4 1 109 ManuellFür unsere ANCOVA konzentrieren wir uns auf drei Variablen:
-
mpg(miles per gallon): Kraftstoffverbrauch - unsere abhängige Variable- Achtung: Im Gegensatz zur in Deutschland üblichen Einheit Liter pro 100 km, gilt bei miles per gallon ein höherer Wert für einen sparsameren Kraftstoffverbrauch, da der Bezug zwischen gefahrener Strecke und verbrauchtem Kraftstoff umgekehrt ist.
-
am(transmission): Getriebeart (0 = automatik, 1 = manuell) - unser Faktor -
hp(horsepower): Motorleistung in PS - unsere Kovariable
print("Deskriptive Statistik nach Getriebearten:")
desc_stats = mtcars_clean.groupby('transmission')[['mpg', 'hp']].agg(['mean', 'std', 'count'])
print(desc_stats.round(2))Deskriptive Statistik nach Getriebearten:
mpg hp
mean std count mean std count
transmission
Automatik 17.15 3.83 19 160.26 53.91 19
Manuell 24.39 6.17 13 126.85 84.06 13Bevor wir mit der eigentlichen ANCOVA beginnen, verschaffen wir uns einen ersten Überblick über unsere Daten. Die deskriptive Statistik zeigt bereits interessante Unterschiede zwischen den Getriebearten, die wir in der folgenden Abbildung genauer betrachten:
Code zeigen/verstecken
# Explorative Datenanalyse
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5), layout='tight')
# Links: Kraftstoffverbrauch nach Getriebeart (Stufenvergleich)
# Jitter für bessere Sichtbarkeit
np.random.seed(42)
for i, transmission in enumerate(['Automatik', 'Manuell']):
data = mtcars_clean[mtcars_clean['transmission'] == transmission]
x_jitter = np.random.normal(i, 0.05, len(data))
ax1.scatter(x_jitter, data['mpg'], alpha=0.7, s=60,
color=transmission_colors[transmission])
# Mittelwert als gestrichelte Linie für jede Gruppe
mean_val = data['mpg'].mean()
ax1.hlines(y=mean_val, xmin=i-0.2, xmax=i+0.2,
colors="black", linestyles='--', linewidth=2)
ax1.set_xticks([0, 1])
ax1.set_xticklabels(['Automatik', 'Manuell'])
ax1.set_ylabel('Kraftstoffverbrauch (mpg)')
ax1.set_title('Kraftstoffverbrauch nach Getriebeart')
# Rechts: Scatterplot Motorleistung vs. Kraftstoffverbrauch
ax2.scatter(mtcars_clean['hp'], mtcars_clean['mpg'], alpha=0.7, s=60, color='gray')
ax2.set_xlabel('Motorleistung (PS)')
ax2.set_ylabel('Kraftstoffverbrauch (mpg)')
ax2.set_title('Kraftstoffverbrauch vs. Motorleistung')
plt.show()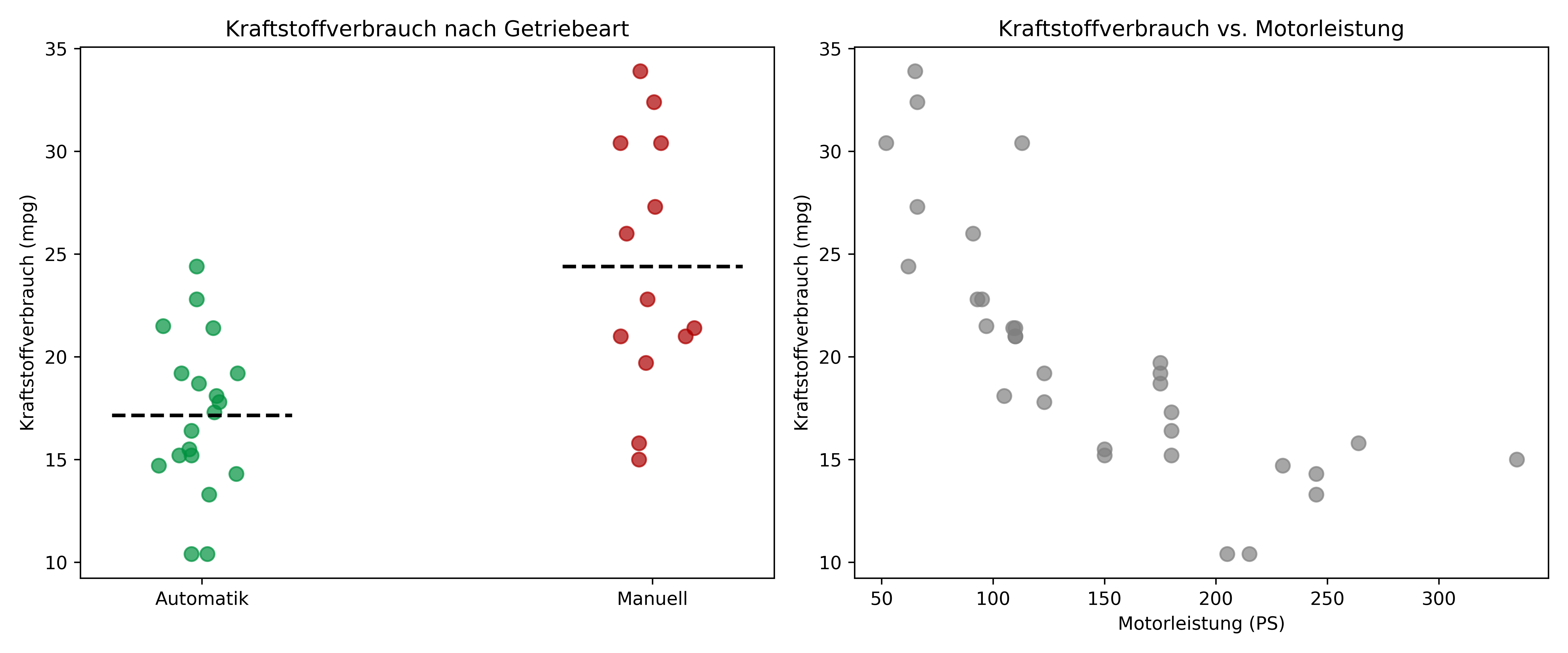
Die linke Grafik bestätigt den deutlichen Unterschied im Kraftstoffverbrauch zwischen den Getriebearten, während die rechte Grafik die Verteilung der Motorleistung in unserem Datensatz zeigt.
Schritt 1: Einfache ANOVA (nur Getriebeart)
Beginnen wir mit einer einfachen ANOVA, die nur die Getriebeart berücksichtigt:
# Einfache ANOVA: mpg ~ transmission
model_anova = smf.ols('mpg ~ C(transmission)', data=mtcars_clean).fit()
anova_simple = sm.stats.anova_lm(model_anova, typ=2)
print("ANOVA: Kraftstoffverbrauch ~ Getriebeart")
print(anova_simple.round(5))
print(f"\nKoeffizienten:")
print(model_anova.params)
print(f"\nR² = {model_anova.rsquared:.3f}")ANOVA: Kraftstoffverbrauch ~ Getriebeart
sum_sq df F PR(>F)
C(transmission) 405.15059 1.0 16.86028 0.00029
Residual 720.89660 30.0 NaN NaN
Koeffizienten:
Intercept 17.147368
C(transmission)[T.Manuell] 7.244939
dtype: float64
R² = 0.360Die ANOVA zeigt einen signifikanten Unterschied (p < 0.001) zwischen Automatik- und Schaltgetrieben. Manuelle Getriebe scheinen im Durchschnitt deutlich sparsamer zu sein.
Schritt 2: Das Problem der konfundierenden Variable
Aber ist dieser Unterschied fair? Schauen wir uns die Verteilung der Motorleistung (PS) zwischen den beiden Getriebearten an:
Code zeigen/verstecken
# Visualisierung der PS-Verteilung nach Getriebeart
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
# Scatterplot: PS vs. Kraftstoffverbrauch, gefärbt nach Getriebeart
for transmission in ['Automatik', 'Manuell']:
data = mtcars_clean[mtcars_clean['transmission'] == transmission]
ax.scatter(data['hp'], data['mpg'], alpha=0.7, s=80,
label=transmission, color=transmission_colors[transmission])
# Gruppenmittelwerte als Rauten einzeichnen
for transmission in ['Automatik', 'Manuell']:
data = mtcars_clean[mtcars_clean['transmission'] == transmission]
mean_hp = data['hp'].mean()
mean_mpg = data['mpg'].mean()
color = transmission_colors[transmission]
ax.scatter(mean_hp, mean_mpg, marker='D', s=200, color=color,
edgecolor='black', linewidth=2, zorder=5,
label=f'{transmission} (Mittelwert)')
ax.set_xlabel('Motorleistung (PS)')
ax.set_ylabel('Kraftstoffverbrauch (mpg)')
ax.set_title('Kraftstoffverbrauch vs. Motorleistung nach Getriebeart')
ax.legend()
plt.show()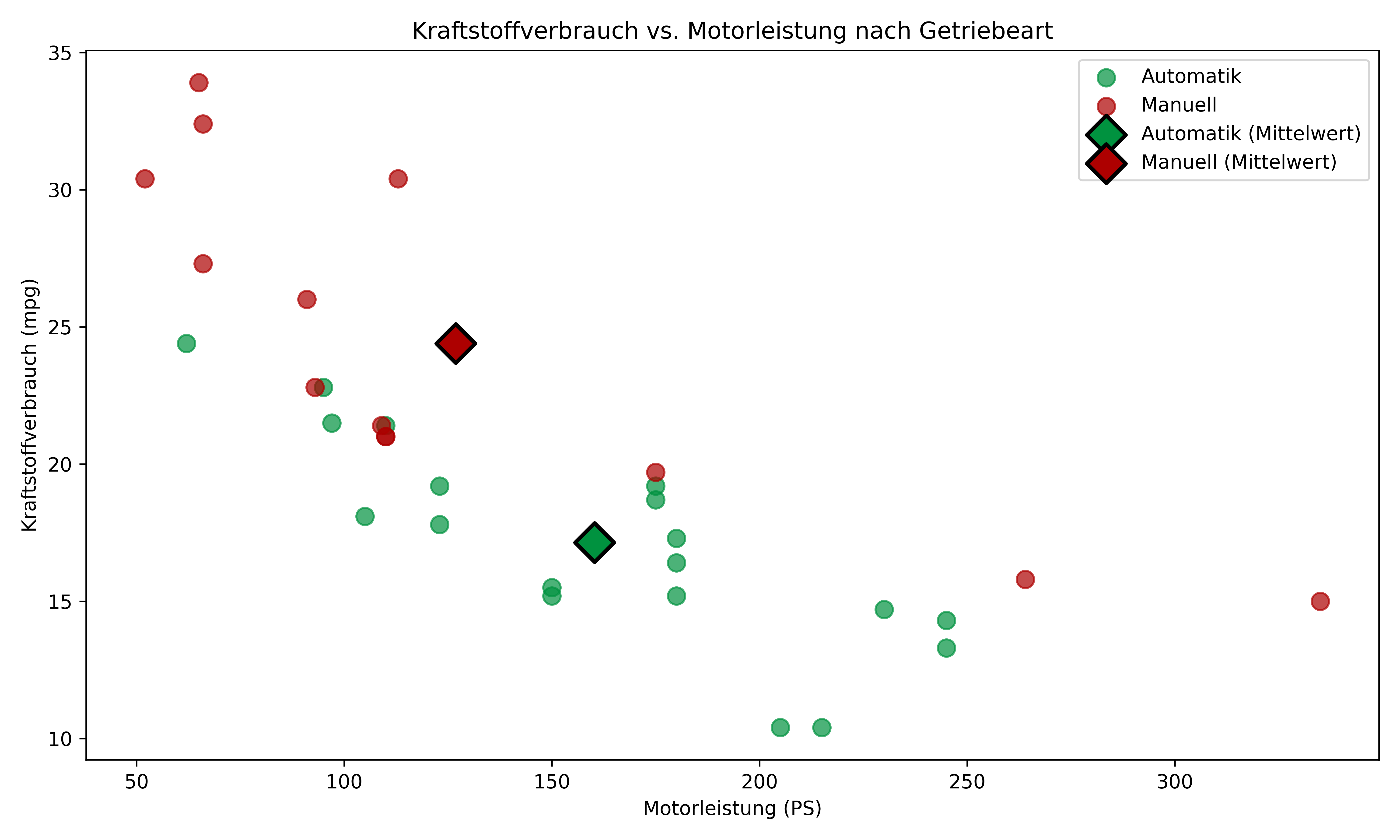
Hier wird das Problem deutlich: Die Fahrzeuge mit Automatikgetriebe in diesem Datensatz haben im Durchschnitt deutlich mehr PS als die mit manuellen Getrieben! Die Rauten zeigen die Gruppenmittelwerte - aber diese liegen bei unterschiedlichen PS-Werten. Dies ist eine konfundierende Variable - der scheinbare Vorteil manueller Getriebe könnte einfach daran liegen, dass sie tendenziell in schwächeren (und damit sparsameren) Fahrzeugen verbaut werden.
Im Idealfall möchten wir ja wissen, ob die Getriebeart selbst einen Einfluss auf den Kraftstoffverbrauch hat, unabhängig von der Motorleistung. Leider haben wir aber zumindest in diesem Datensatz keine gleichmäßige Verteilung der Motorleistung zwischen den Getriebearten.
Das Problem konfundierender Variablen begegnet uns in vielen Bereichen:
Marketing: Kunden, die Newsletter abonniert haben, kaufen mehr. Ist der Newsletter so überzeugend? Oder sind Newsletter-Abonnenten einfach generell kauffreudigere und engagiertere Kunden?
Ernährung: Menschen, die täglich Vitaminpräparate nehmen, sind gesünder. Liegt es an den Vitaminen oder daran, dass diese Personen generell einen gesünderen Lebensstil (mehr Sport, bewusstere Ernährung) pflegen?
Technik: Laptops der Marke X haben weniger Reparaturen. Ist die Qualität besser? Oder werden diese Geräte hauptsächlich von weniger intensiven Nutzern verwendet?
Ökologie: In Gebieten mit mehr Bäumen leben mehr Vogelarten. Liegt es an den Bäumen selbst oder an anderen Faktoren wie Wasserverfügbarkeit, Klima oder geringerer Urbanisierung, die sowohl Bäume als auch Vögel begünstigen?
Bildungsforschung: Schüler aus Privatschulen schneiden bei Standardtests besser ab. Ist das der Beweis für bessere Privatschulen? Oder erklärt der sozioökonomische Hintergrund der Familien (höhere Bildung der Eltern, mehr Unterstützung zu Hause) den Unterschied?
Schritt 3: Test auf Interaktion - Voraussetzung für ANCOVA
Bevor wir eine ANCOVA durchführen können, müssen wir eine wichtige Voraussetzung1 prüfen: Es darf keine signifikante Interaktion zwischen dem Faktor (Getriebeart) und der Kovariable (Motorleistung) geben. Nur wenn diese Voraussetzung erfüllt ist, können wir sinnvoll für die Kovariable “korrigieren”.
# Test auf Interaktion: Vollständiges Modell mit Interaktionsterm
model_interaction = smf.ols('mpg ~ C(transmission) * hp', data=mtcars_clean).fit()
anova_interaction = sm.stats.anova_lm(model_interaction, typ=3)
print("Modell mit Interaktion: mpg ~ transmission * hp")
print(anova_interaction.round(5))
print(f"\nKoeffizienten:")
print(model_interaction.params.round(3))
print(f"\nR² = {model_interaction.rsquared:.3f}")Modell mit Interaktion: mpg ~ transmission * hp
sum_sq df F PR(>F)
Intercept 1303.96568 1.0 148.76111 0.00000
C(transmission) 33.59715 1.0 3.83288 0.06029
hp 182.93652 1.0 20.87006 0.00009
C(transmission):hp 0.00525 1.0 0.00060 0.98065
Residual 245.43404 28.0 NaN NaN
Koeffizienten:
Intercept 26.625
C(transmission)[T.Manuell] 5.218
hp -0.059
C(transmission)[T.Manuell]:hp 0.000
dtype: float64
R² = 0.782Wie wir sehen können, ist die Interaktion nicht signifikant (p > 0.05). Das ist wichtig, denn es bedeutet, dass der Einfluss der Motorleistung auf den Kraftstoffverbrauch für beide Getriebearten gleich ist. Mit anderen Worten: Die Steigung der Beziehung zwischen PS und mpg ist für Automatik- und Schaltgetriebe parallel.
Interessant ist auch, dass in diesem Modell mit Interaktionsterm der Haupteffekt der Getriebeart nicht mehr signifikant ist (p > 0.05). Das zeigt bereits, dass die Motorleistung der wichtigere erklärende Faktor ist und dass nach Kontrolle für die PS der Unterschied zwischen den Getriebearten stark abnimmt - genau das, was wir schon in Schritt 2 anhand der Rauten (Gruppenmittelwerte bei unterschiedlichen PS-Werten) vermutet haben.
Schritt 4: ANCOVA - das korrigierte Modell
Da die Interaktion nicht signifikant ist, können wir sie aus dem Modell entfernen und die eigentliche ANCOVA durchführen:
# ANCOVA: mpg ~ transmission + hp (ohne Interaktion)
model_ancova = smf.ols('mpg ~ C(transmission) + hp', data=mtcars_clean).fit()
anova_ancova = sm.stats.anova_lm(model_ancova, typ=2)
print("ANCOVA: mpg ~ transmission + hp")
print(anova_ancova.round(5))
print(f"\nKoeffizienten:")
print(model_ancova.params.round(3))
print(f"\nR² = {model_ancova.rsquared:.3f}")
print(f"Adjustiertes R² = {model_ancova.rsquared_adj:.3f}")ANCOVA: mpg ~ transmission + hp
sum_sq df F PR(>F)
C(transmission) 202.23503 1.0 23.89518 0.00003
hp 475.45731 1.0 56.17789 0.00000
Residual 245.43929 29.0 NaN NaN
Koeffizienten:
Intercept 26.585
C(transmission)[T.Manuell] 5.277
hp -0.059
dtype: float64
R² = 0.782
Adjustiertes R² = 0.767Das mathematische Modell der ANCOVA lautet:
\[\text{mpg}_i = \beta_0 + \beta_1 \cdot \text{transmission}_i + \beta_2 \cdot \text{hp}_i + \varepsilon_i\]
Dabei ist transmission eine Dummy-Variable (0 für Automatik, 1 für Manuell).
Interessant: Nachdem wir die nicht-signifikante Interaktion entfernt haben, wird der Haupteffekt der Getriebeart wieder leicht signifikant (je nach exakten p-Werten). Dies zeigt die Feinheiten statistischer Modellierung - kleine Änderungen im Modell können die Signifikanz beeinflussen.
Schritt 5: Visualisierung der parallelen Regressionsgeraden
Die ANCOVA geht von parallelen Regressionsgeraden aus - beide Getriebearten haben die gleiche Steigung bezüglich der Motorleistung, aber möglicherweise unterschiedliche Achsenabschnitte:
Code zeigen/verstecken
# Visualisierung der ANCOVA: Parallele Regressionsgeraden
fig, ax = plt.subplots(figsize=(10, 6), layout='tight')
# Datenpunkte
for transmission in ['Automatik', 'Manuell']:
data = mtcars_clean[mtcars_clean['transmission'] == transmission]
ax.scatter(data['hp'], data['mpg'], alpha=0.7, s=80,
label=transmission, color=transmission_colors[transmission])
# Parallele Regressionsgeraden (ANCOVA-Modell)
hp_range = np.linspace(mtcars_clean['hp'].min(), mtcars_clean['hp'].max(), 100)
# Koeffizienten aus dem ANCOVA-Modell
intercept = model_ancova.params[0]
transmission_effect = model_ancova.params[1]
hp_effect = model_ancova.params[2]
# Automatik (transmission = 0)
y_auto = intercept + hp_effect * hp_range
ax.plot(hp_range, y_auto, color=transmission_colors['Automatik'], linewidth=2, linestyle='--',
label='Automatik (ANCOVA)')
# Manuell (transmission = 1)
y_manual = (intercept + transmission_effect) + hp_effect * hp_range
ax.plot(hp_range, y_manual, color=transmission_colors['Manuell'], linewidth=2, linestyle='--',
label='Manuell (ANCOVA)')
# Ursprüngliche Gruppenmittelwerte als transparente Rauten (aus Schritt 2)
for transmission in ['Automatik', 'Manuell']:
data = mtcars_clean[mtcars_clean['transmission'] == transmission]
mean_hp = data['hp'].mean()
mean_mpg = data['mpg'].mean()
color = transmission_colors[transmission]
ax.scatter(mean_hp, mean_mpg, marker='D', s=200, color=color,
alpha=0.5, edgecolor='black', linewidth=1, zorder=4,
label=f'{transmission} (urspr. Mittelwert)')
# Korrigierte Werte bei durchschnittlicher PS als Dreiecke
mean_hp_overall = mtcars_clean['hp'].mean()
# Vorhersagen bei durchschnittlicher PS
y_auto_corrected = intercept + hp_effect * mean_hp_overall
y_manual_corrected = (intercept + transmission_effect) + hp_effect * mean_hp_overall
ax.scatter(mean_hp_overall, y_auto_corrected, marker='^', s=200,
color=transmission_colors['Automatik'], edgecolor='black', linewidth=2, zorder=5,
label=f'Automatik (korrigiert bei {mean_hp_overall:.1f} PS)')
ax.scatter(mean_hp_overall, y_manual_corrected, marker='^', s=200,
color=transmission_colors['Manuell'], edgecolor='black', linewidth=2, zorder=5,
label=f'Manuell (korrigiert bei {mean_hp_overall:.1f} PS)')
# Vertikale Linie bei durchschnittlicher PS
ax.axvline(x=mean_hp_overall, color='gray', linestyle=':', alpha=0.7,
label=f'Durchschnittliche PS ({mean_hp_overall:.1f})')
ax.set_xlabel('Motorleistung (PS)')
ax.set_ylabel('Kraftstoffverbrauch (mpg)')
ax.set_title('ANCOVA: Parallele Regressionsgeraden mit Korrektureffekt')
ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.show()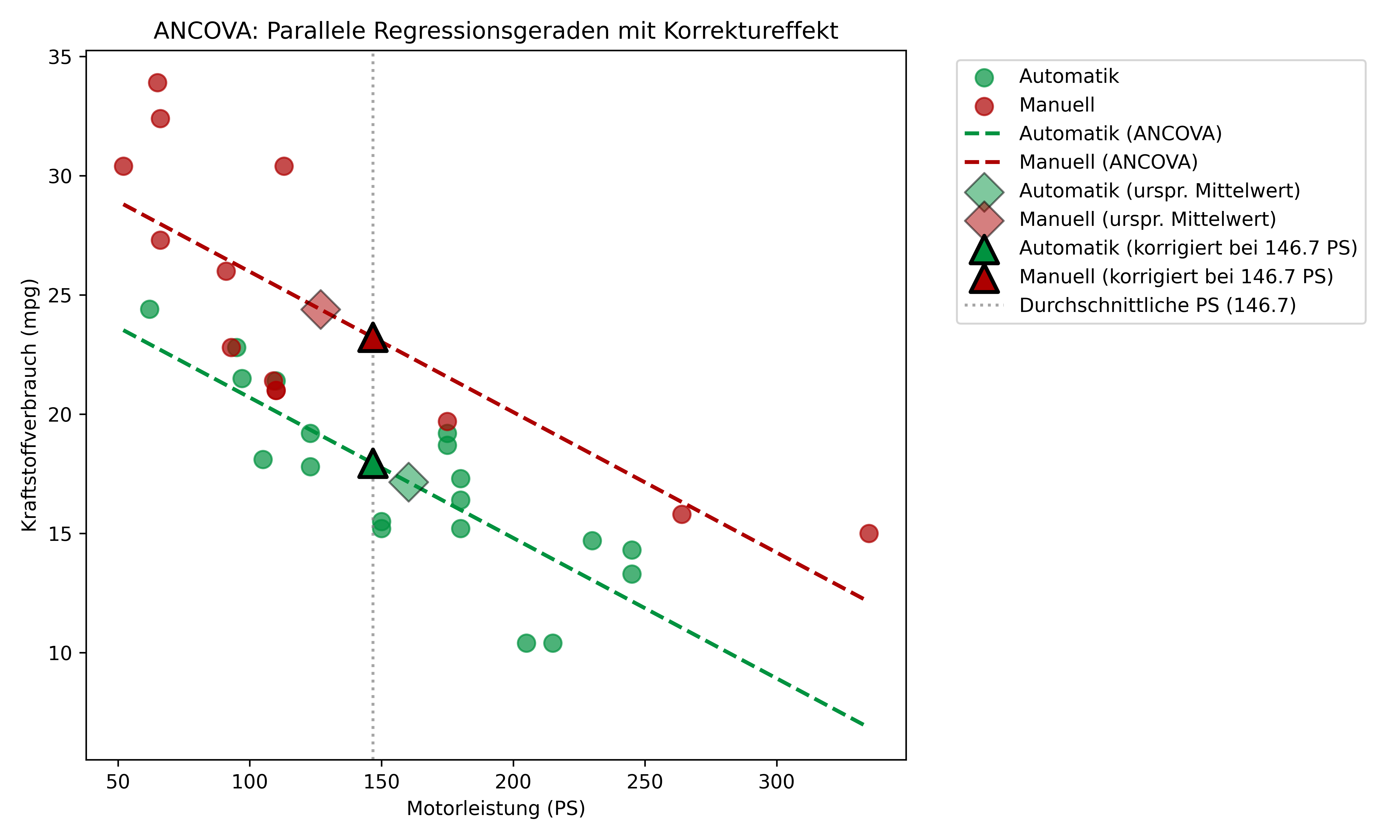
Die parallelen Geraden zeigen das Kernprinzip der ANCOVA: Der Effekt der Motorleistung auf den Kraftstoffverbrauch ist für beide Getriebearten gleich (gleiche Steigung), aber die Ausgangsniveaus können sich unterscheiden.
Die transparenten Rauten zeigen nochmals die ursprünglichen Gruppenmittelwerte aus Schritt 2 - diese lagen bei unterschiedlichen PS-Werten und führten zu einem “unfairen” Vergleich. Die Dreiecke hingegen zeigen die korrigierten Werte bei der durchschnittlichen Motorleistung von 146.7 PS. Der Abstand zwischen den Dreiecken ist deutlich kleiner als zwischen den Rauten - das ist der Korrektureffekt der ANCOVA!
Schritt 6: Der Korrektureffekt - Vorher vs. Nachher
Um zu verdeutlichen, wie stark die Kovariable unsere Schlüsse beeinflusst, vergleichen wir die ursprünglichen Mittelwerte mit den korrigierten Werten:
# Vergleich: Ursprüngliche vs. korrigierte Mittelwerte
print("Der Korrektureffekt der ANCOVA:")
print("=" * 40)
# 1. Ursprüngliche Mittelwerte
print("\n1. Ursprüngliche Mittelwerte (ohne Korrektur):")
original_means = mtcars_clean.groupby('transmission')['mpg'].mean()
for transmission in ['Automatik', 'Manuell']:
print(f" {transmission}: {original_means[transmission]:.2f} mpg")
original_diff = original_means['Manuell'] - original_means['Automatik']
print(f" Unterschied (Manuell - Automatik): {original_diff:.2f} mpg")
# 2. Korrigierte Werte bei durchschnittlicher PS
mean_hp = mtcars_clean['hp'].mean()
print(f"\n2. Korrigierte Werte bei durchschnittlicher PS ({mean_hp:.1f} PS):")
# Vorhersagen bei durchschnittlicher PS
pred_data = pd.DataFrame({
'transmission': ['Automatik', 'Manuell'],
'hp': [mean_hp, mean_hp]
})
predictions = model_ancova.predict(pred_data)
for i, transmission in enumerate(['Automatik', 'Manuell']):
print(f" {transmission}: {predictions.iloc[i]:.2f} mpg")
corrected_diff = predictions.iloc[1] - predictions.iloc[0]
print(f" Unterschied (korrigiert): {corrected_diff:.2f} mpg")
# 3. Zusammenfassung der Veränderung
print(f"\n3. Zusammenfassung:")
reduction = abs(original_diff) - abs(corrected_diff)
percentage_reduction = (reduction / abs(original_diff)) * 100
print(f" Reduktion des Unterschieds: {reduction:.2f} mpg ({percentage_reduction:.1f}%)")
print(f"\n4. Visueller Vergleich:")
print(f" Rauten in Schritt 2: Zeigen den ursprünglichen Unterschied von {original_diff:.2f} mpg")
print(f" Dreiecke in Schritt 5: Zeigen den korrigierten Unterschied von {corrected_diff:.2f} mpg")
print(f" → Die ANCOVA 'schiebt' die Vergleichspunkte auf eine faire Linie!")Der Korrektureffekt der ANCOVA:
========================================
1. Ursprüngliche Mittelwerte (ohne Korrektur):
Automatik: 17.15 mpg
Manuell: 24.39 mpg
Unterschied (Manuell - Automatik): 7.24 mpg
2. Korrigierte Werte bei durchschnittlicher PS (146.7 PS):
Automatik: 17.95 mpg
Manuell: 23.22 mpg
Unterschied (korrigiert): 5.28 mpg
3. Zusammenfassung:
Reduktion des Unterschieds: 1.97 mpg (27.2%)
4. Visueller Vergleich:
Rauten in Schritt 2: Zeigen den ursprünglichen Unterschied von 7.24 mpg
Dreiecke in Schritt 5: Zeigen den korrigierten Unterschied von 5.28 mpg
→ Die ANCOVA 'schiebt' die Vergleichspunkte auf eine faire Linie!ANCOVA-Fazit: Die Kovariable “Motorleistung” erklärt einen großen Teil der Variation im Kraftstoffverbrauch. Nach Kontrolle für die PS wird der Unterschied zwischen den Getriebearten deutlich kleiner. Dies zeigt, wie wichtig es ist, konfundierende Variablen in der Analyse zu berücksichtigen, um faire Vergleiche zwischen Gruppen zu ermöglichen.
Teil 2: Moderationsanalyse
Während die ANCOVA keine Interaktion zwischen Faktor und Kovariable voraussetzt, gibt es Situationen, in denen diese Interaktion durchaus von Interesse ist. Wenn die Beziehung zwischen der Kovariable und der abhängigen Variable je nach Gruppe unterschiedlich ist, sprechen wir von einer Moderationsanalyse.
Palmer Penguins: Arten moderieren die Beziehung
Kehren wir zu unserem Palmer Penguins Beispiel zurück und untersuchen, ob die Pinguinart die Beziehung zwischen Schnabeltiefe und Körpergewicht moderiert:
# Moderationsanalyse: body_mass_g ~ species * bill_depth_mm
model_moderation = smf.ols('body_mass_g ~ C(species) * bill_depth_mm', data=penguins_clean).fit()
anova_moderation = sm.stats.anova_lm(model_moderation, typ=3)
print("Moderationsanalyse: Körpergewicht ~ Art × Schnabeltiefe")
print(anova_moderation.round(5))
print(f"\nKoeffizienten:")
for param, value in model_moderation.params.items():
print(f"{param}: {value:.2f}")
print(f"\nR² = {model_moderation.rsquared:.3f}")
print(f"Adjustiertes R² = {model_moderation.rsquared_adj:.3f}")Moderationsanalyse: Körpergewicht ~ Art × Schnabeltiefe
sum_sq df F PR(>F)
Intercept 5.270569e+04 1.0 0.41841 0.51818
C(species) 3.098247e+04 2.0 0.12298 0.88432
bill_depth_mm 1.047004e+07 1.0 83.11681 0.00000
C(species):bill_depth_mm 2.074479e+06 2.0 8.23416 0.00032
Residual 4.232519e+07 336.0 NaN NaN
Koeffizienten:
Intercept: -283.28
C(species)[T.Chinstrap]: 247.06
C(species)[T.Gentoo]: -175.71
bill_depth_mm: 217.15
C(species)[T.Chinstrap]:bill_depth_mm: -12.53
C(species)[T.Gentoo]:bill_depth_mm: 152.29
R² = 0.807
Adjustiertes R² = 0.804Das mathematische Modell der Moderationsanalyse lautet:
\[\text{body\_mass}_i = \beta_0 + \beta_1 \cdot \text{species1}_i + \beta_2 \cdot \text{species2}_i + \beta_3 \cdot \text{bill\_depth}_i\] \[+ \beta_4 \cdot \text{species1}_i \cdot \text{bill\_depth}_i + \beta_5 \cdot \text{species2}_i \cdot \text{bill\_depth}_i + \varepsilon_i\]
Visualisierung: Drei verschiedene Regressionsgeraden
Im Gegensatz zur ANCOVA mit parallelen Geraden erhalten wir hier drei unterschiedliche Regressionsgeraden:
Code zeigen/verstecken
# Visualisierung der Moderationsanalyse
fig, ax = plt.subplots(figsize=(12, 8), layout='tight')
# Datenpunkte nach Arten
for species in penguins_clean['species'].unique():
data = penguins_clean[penguins_clean['species'] == species]
ax.scatter(data['bill_depth_mm'], data['body_mass_g'],
alpha=0.7, color=colors[species], s=60, label=f'{species} (Daten)')
# Separate Regressionsgeraden für jede Art basierend auf dem Interaktionsmodell
bill_depth_range = np.linspace(penguins_clean['bill_depth_mm'].min(),
penguins_clean['bill_depth_mm'].max(), 100)
# Einfachere Methode: Separate Modelle für jede Art
species_list = penguins_clean['species'].unique()
for species in species_list:
species_data = penguins_clean[penguins_clean['species'] == species]
species_model = smf.ols('body_mass_g ~ bill_depth_mm', data=species_data).fit()
# Vorhersagen für diese Art
x_range_species = np.linspace(species_data['bill_depth_mm'].min(),
species_data['bill_depth_mm'].max(), 50)
y_pred_species = species_model.predict(pd.DataFrame({'bill_depth_mm': x_range_species}))
ax.plot(x_range_species, y_pred_species, color=colors[species], linewidth=3,
label=f'{species} (Regression)')
ax.set_xlabel('Schnabeltiefe (mm)')
ax.set_ylabel('Körpergewicht (g)')
ax.set_title('Moderationsanalyse: Verschiedene Steigungen und Achsenabschnitte')
ax.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.show()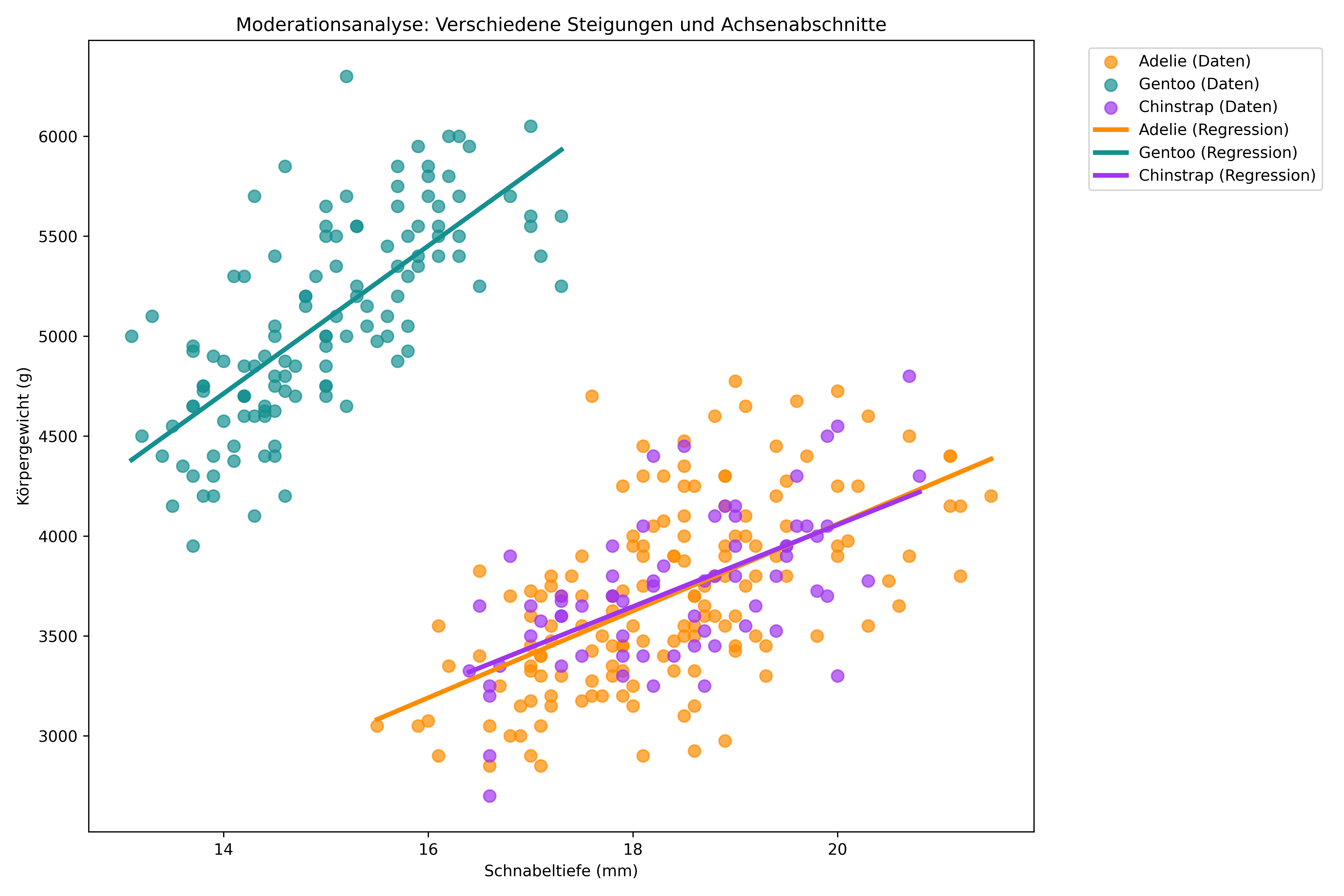
Eine häufige Frage ist: Warum brauchen wir den bill_depth_mm Term, wenn wir doch schon C(species):bill_depth_mm haben?
Die Antwort liegt mal wieder in der Referenzgruppen-Parametrisierung: Der Haupteffekt bill_depth_mm ist die Steigung für die Referenzgruppe (hier: Adelie-Pinguine). Die Interaktionsterme zeigen dann die Abweichungen von dieser Referenz-Steigung für die anderen Arten.
So entstehen die drei verschiedenen Steigungen: - Adelie: Referenz-Steigung (Koeffizient von bill_depth_mm) - Chinstrap: Referenz-Steigung + Interaktions-Koeffizient
- Gentoo: Referenz-Steigung + Interaktions-Koeffizient
Der dramatische Unterschied: Simpson’s Paradox in Aktion
Hier wird besonders deutlich, warum die Moderationsanalyse so wichtig ist. Ohne Berücksichtigung der Pinguinarten hätten wir einen völlig falschen Schluss gezogen!
Erinnern wir uns an die erste Analyse:
- Einfache Regression (ignoriert Arten): Schwach negativer Zusammenhang (R² = 0.056)
- Interpretation: “Mit zunehmender Schnabeltiefe nimmt das Körpergewicht ab”
Aber die Moderationsanalyse zeigt das Gegenteil:
- Artspezifische Regressionen: Alle drei Steigungen sind positiv!
- Korrekte Interpretation: “Innerhalb jeder Art nimmt das Körpergewicht mit zunehmender Schnabeltiefe zu”
Dieses Phänomen ist ein klassisches Beispiel für Simpson’s Paradox: Ein Trend in aggregierten Daten verschwindet oder kehrt sich sogar um, wenn die Daten in sinnvolle Untergruppen aufgeteilt werden. Die scheinbar negative Gesamtbeziehung entsteht nur dadurch, dass:
- Gentoo-Pinguine generell schwerer sind UND größere Schnäbel haben
-
Adelie-Pinguine generell leichter sind UND kleinere Schnäbel haben
- Die Unterschiede zwischen den Arten überlagern die innerartlichen Beziehungen
Ohne die Berücksichtigung der Moderation durch die Pinguinart hätten wir eine biologisch unsinnige Schlussfolgerung gezogen. Die Moderationsanalyse deckt die wahren, biologisch plausiblen Zusammenhänge auf: Innerhalb jeder Art sind dickere Schnäbel mit höherem Körpergewicht assoziiert.
Übersicht: Die fünf Grundszenarien
Zum Abschluss betrachten wir eine systematische Übersicht über die verschiedenen Modelltypen, die wir nun kennengelernt haben. Diese Szenarien unterscheiden sich darin, welche Parameter in der linearen Gleichung enthalten sind:
Code zeigen/verstecken
# Künstliche Daten für die Demonstration der Grundszenarien
np.random.seed(42)
x = np.linspace(0, 10, 100)
fig, axes = plt.subplots(2, 3, figsize=(15, 10), layout='tight')
axes = axes.flatten()
# Szenario 1: Nur Achsenabschnitt (y ~ 1)
y1 = 5 + np.random.normal(0, 0.5, 100)
axes[0].scatter(x, y1, alpha=0.6, s=30)
axes[0].axhline(y=5, color='red', linewidth=2)
axes[0].set_title('Szenario 1:\nEin Achsenabschnitt\nKeine Steigung\ny ~ 1')
axes[0].set_xlabel('x')
axes[0].set_ylabel('y')
# Szenario 2: Nur Steigung (y ~ x - 1)
y2 = 0.5 * x + np.random.normal(0, 0.5, 100)
axes[1].scatter(x, y2, alpha=0.6, s=30)
axes[1].plot(x, 0.5 * x, color='red', linewidth=2)
axes[1].set_title('Szenario 2:\nKein Achsenabschnitt\nEine Steigung\ny ~ x - 1')
axes[1].set_xlabel('x')
axes[1].set_ylabel('y')
# Szenario 3: Faktor mit 2 Stufen (y ~ factor)
group = np.repeat([0, 1], 50)
y3 = 3 + 2 * group + np.random.normal(0, 0.5, 100)
colors_simple = ['blue', 'orange']
for g in [0, 1]:
mask = group == g
axes[2].scatter(x[mask], y3[mask], alpha=0.6, s=30, color=colors_simple[g],
label=f'Gruppe {g+1}')
axes[2].axhline(y=3 + 2*g, color=colors_simple[g], linewidth=2)
axes[2].set_title('Szenario 3:\nMehrere Achsenabschnitte\nKeine Steigung\ny ~ factor')
axes[2].set_xlabel('x')
axes[2].set_ylabel('y')
axes[2].legend()
# Szenario 4: Zwei verschiedene Steigungen (y ~ x:factor - 1)
y4 = (0.3 + 0.4 * group) * x + np.random.normal(0, 0.5, 100)
for g in [0, 1]:
mask = group == g
axes[3].scatter(x[mask], y4[mask], alpha=0.6, s=30, color=colors_simple[g],
label=f'Gruppe {g+1}')
axes[3].plot(x, (0.3 + 0.4*g) * x, color=colors_simple[g], linewidth=2)
axes[3].set_title('Szenario 4:\nKein Achsenabschnitt\nMehrere Steigungen\ny ~ x:factor - 1')
axes[3].set_xlabel('x')
axes[3].set_ylabel('y')
axes[3].legend()
# Szenario 5: Vollständige Regressionsgeraden (y ~ x * factor)
y5 = (2 + 3 * group) + (0.3 + 0.4 * group) * x + np.random.normal(0, 0.5, 100)
for g in [0, 1]:
mask = group == g
axes[4].scatter(x[mask], y5[mask], alpha=0.6, s=30, color=colors_simple[g],
label=f'Gruppe {g+1}')
axes[4].plot(x, (2 + 3*g) + (0.3 + 0.4*g) * x, color=colors_simple[g], linewidth=2)
axes[4].set_title('Szenario 5:\nMehrere Achsenabschnitte\nMehrere Steigungen\ny ~ x * factor')
axes[4].set_xlabel('x')
axes[4].set_ylabel('y')
axes[4].legend()
# Leeres Subplot entfernen
axes[5].remove()
plt.tight_layout()
plt.show()
Die ANCOVA entspricht einem Spezialfall ohne Interaktionsterm2, während die Moderationsanalyse dem vollständigen Szenario 5 entspricht.
Unterschied zwischen ANCOVA und Moderationsanalyse
Zusammenfassend lässt sich der Hauptunterschied so formulieren:
ANCOVA (Analysis of Covariance):
- Annahme: Keine Interaktion zwischen Faktor und Kovariable
-
Ergebnis: Parallele Regressionsgeraden (gleiche Steigung, verschiedene Achsenabschnitte)
- Interpretation: Die Kovariable hilft dabei, “fairere” Gruppenvergleiche zu erstellen
- Verwendung: Wenn man Gruppenunterschiede um eine kontinuierliche Variable bereinigen möchte
Moderationsanalyse:
- Annahme: Interaktion zwischen Faktor und kontinuierlicher Variable ist von Interesse
- Ergebnis: Verschiedene Regressionsgeraden (verschiedene Steigungen UND Achsenabschnitte)
- Interpretation: Der Faktor moderiert die Beziehung zwischen kontinuierlicher und abhängiger Variable
- Verwendung: Wenn der Zusammenhang zwischen zwei Variablen gruppenspezifisch ist
Beide Ansätze sind wichtige Werkzeuge in der statistischen Modellierung und ergänzen die Palette der linearen Modelle, die wir in den vorangegangenen Kapiteln kennengelernt haben. Sie zeigen, wie flexibel und mächtig der Rahmen der linearen Modelle ist, um komplexe Beziehungen zwischen verschiedenen Arten von Variablen zu modellieren.